python解析法解决一元线性回归

课程链接

链接: link.

解析法求一元线性

求面积与房价的线性关系

理论基础

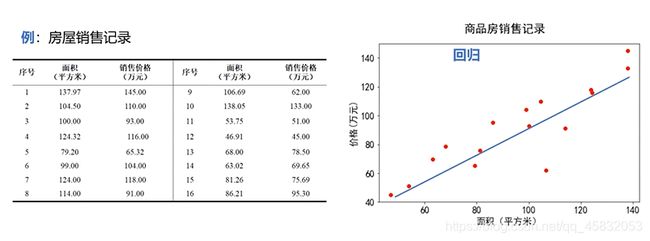
求解问题：求一理想直线最能描述样本点增长趋势

具体：求直线的 w ，b

基本思想：
一、求样本点到理想直线的距离，当样本点到直线距离之和最小(残差绝对值最小)，看作这时是最好的拟合直线，因为绝对值不好进行公式计算变换，且一个函数平方最小(残差平方和最小)也是其绝对值最小，因此我们采用残差平方和最小求解 w ，b

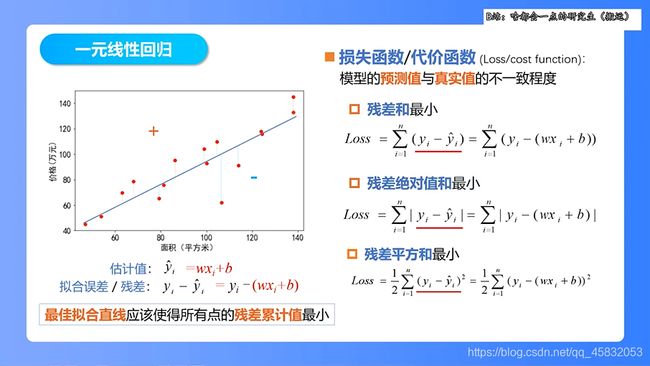
二、用残差平方和最小分别对 w ，b 求偏导，当它们为0时表示两个分别在 w ，b 方向上的残差平方和最小最小函数，两函数交点即为最佳的 w ，b
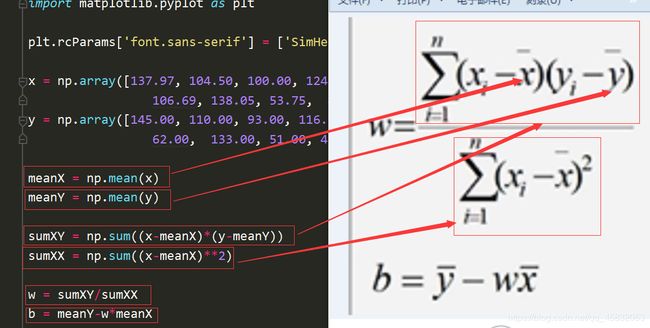
最佳 w ，b 计算结果如下图右边，python编程不需了解计算过程，直接利用结果就行

代码

公式部分代码解释

import numpy as np

import matplotlib.pyplot as plt 

plt.rcParams['font.sans-serif'] = ['SimHei'] #为避免画图时用中文时报错

x = np.array([137.97, 104.50, 100.00, 124.32, 79.20, 99.00, 124.00, 114.00,
                 106.69, 138.05, 53.75,  46.91,  68.00, 63.02, 81.26,  86.21])
y = np.array([145.00, 110.00, 93.00, 116.00,  65.32, 104.00, 118.00, 91.00,
                 62.00,  133.00, 51.00, 45.00,   78.50, 69.65,  75.69,  95.30])

meanX = np.mean(x)
meanY = np.mean(y)

sumXY = np.sum((x-meanX)*(y-meanY))
sumXX = np.sum((x-meanX)**2)

w = sumXY/sumXX
b = meanY-w*meanX

print("权值w=",w,"\n偏置值b=",b)
print("线性模型：y=",w,"*x+",b)

x_test = np.array([128.15, 45.00, 141.43, 106.27, 99.00, 53.84, 85.36, 70.00])
y_pred = (w*x_test+b)

print("面积\t估计房价")
n = len(x_test)
for i in range(n):
    print(x_test[i],"\t",round(y_pred[i],2))

print(y_pred)

plt.figure()

plt.scatter(x,y,color="red",label="销售记录")
plt.scatter(x_test,y_pred,color="blue",label="预测房价")
plt.plot(x_test,y_pred,color="green",label="拟合直线",linewidth=2)

plt.xlabel("面积(平方米)",fontsize=14)
plt.ylabel("价格(万元)",fontsize=14)

plt.xlim((40,150))
plt.ylim((40,150))

plt.suptitle("商品房销售价格评估系统v1.0",fontsize=20)

plt.legend(loc="upper left")
plt.show()