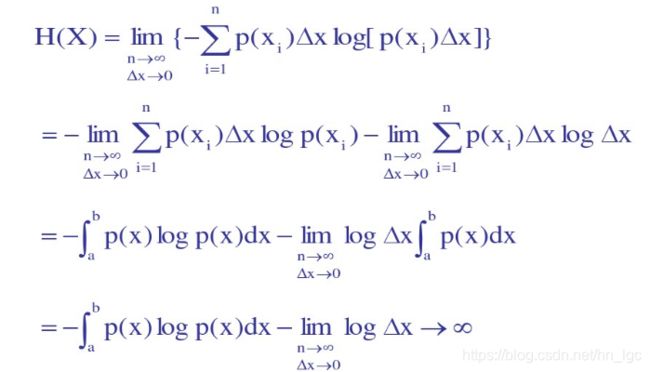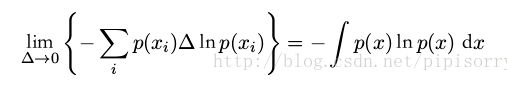信息论的一些知识

随机事件x的信息量：
h(x) = − log 2 p(x)      
随机变量的熵：
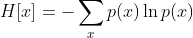
熵的单位
单位取决于定义用到对数的底。当b = 2，熵的单位是bit；当b = e，熵的单位是nat；而当b = 10,熵的单位是 Hart。
熵的取值范围：
0<=H[X]<=log(n)  ， n是事件个数

熵的特性：
连续性
该量度应连续，概率值小幅变化只能引起熵的微小变化。
对称性
符号xi重新排序后，该量度应不变。 
极值性
当所有符号等可能出现的情况下，熵达到最大值（所有可能的事件等概率时不确定性最高）。
可加性
熵的量与该过程如何被划分无关。

增减一概率为零的事件不改变熵。
微分熵：

推导：

对概率密度函数采取微元法

可以看到，微元法直接计算的微分熵值是无穷大，连续随机变量的熵是无穷大的，无法计算了

取前面一部分作为微分熵：

这样定义的目的：
>嫡差具有信息度量的意义
>与离散信源的嫡在形式上统一

因为前面已经减少了一个正无穷大，所以有负值了。

 

香农熵的变型和拓展

联合熵(joint entropy)

就是二维随机变量直接拓展过来的。

 

条件熵(conditional entropy)

可理解为给定X的值前提下随机变量Y的随机性的量。

条件熵 H(Y|X)定义为 X 给定条件下 Y 的条件概率分布的熵对 X 的数学期望：

 

条件熵 H(Y|X)相当于联合熵 H(X,Y)减去单独的熵 H(X)，即H(Y|X)=H(X,Y)−H(X)，证明如下：

举个例子，比如环境温度是低还是高，和我穿短袖还是外套这两个事件可以组成联合概率分布 H(X,Y)，因为两个事件加起来的信息量肯定是大于单一事件的信息量的。假设 H(X)对应着今天环境温度的信息量，由于今天环境温度和今天我穿什么衣服这两个事件并不是独立分布的，所以在已知今天环境温度的情况下，我穿什么衣服的信息量或者说不确定性是被减少了。当已知 H(X) 这个信息量的时候，H(X,Y) 剩下的信息量就是条件熵：H(Y|X)=H(X,Y)−H(X)

因此，可以这样理解，描述 X 和 Y 所需的信息是描述 X 自己所需的信息,加上给定 X的条件下具体化 Y 所需的额外信息。

 

互信息(mutual information)

如果 (X, Y) ~ p(x, y), X, Y 之间的互信息 I(X; Y)定义为:

Note: 互信息 I (X; Y)取值为非负。当X、Y相互独立时，I(X,Y)最小为0。

互信息实际上是更广泛的相对熵的特殊情形

如果变量不是独立的,那么我们可以通过考察联合概率分布与边缘概率分布乘积之间的 Kullback-Leibler 散度来判断它们是否“接近”于相互独立。此时, Kullback-Leibler 散度为

这被称为变量 x 和变量 y 之间的互信息( mutual information )。根据 Kullback-Leibler 散度的性质,我们看到 I[x, y] ≥ 0 ,当且仅当 x 和 y 相互独立时等号成立。

使用概率的加和规则和乘积规则,我们看到互信息和条件熵之间的关系为

可以把互信息看成由于知道 y 值而造成的 x 的不确定性的减小(反之亦然)（即Y的值透露了多少关于X 的信息量）。就是X,Y的公共信息量咯。

 

点互信息：

定义：

点互信息用户衡量两个变量的相关性。是从互信息中引申出来的，形式上可以看做互信息中一个点的信息量，和熵中一个点的信息量类似，熵点的信息量加权累积的得到熵，点互信息加权累加就是互信息了。还可以看做知道y时，x的条件概率p(x|y)与原来的概率p(x)比值求log得到。想一想，衡量两个变量的相关性似乎可以直接用p(x,y)大小来衡量，这样行吗，由于如果x很多，就算x和y一起出现比较少，p(x,y)也大，而如果x,y很少，但是却经常一起出现，p(x,y)还是很小的，就不对了，所以p(x,)不能作为衡量标准，那么在下面处于p(x),p(y)就可以了。就可以看成在x,y的概率条件下，一起出现的概率。然后log，得到信息量。

取值范围：

可以为负，最大为-logp(x)或者-logp(y)

和互信息很多性质类似，比如

h(x)即信息量.

互信息、条件熵与联合熵的区别与联系

venn图表示关系