题—送外卖2(最短路径&&dfs)
送外卖2
图论,动态规划,BFS,弗洛里德算法
感悟:
1.dfs是个好东西,但是要优化喔
2.弗洛里德算法(简单的图,简单粗暴点直接三重for循环)
3.动态规划中的(一个数存取一长串二进制数,)二进制,
对二进制的移位,存取有了新的认识。
dp 拿以前的得到的结果,影响现在或者以后的结果。
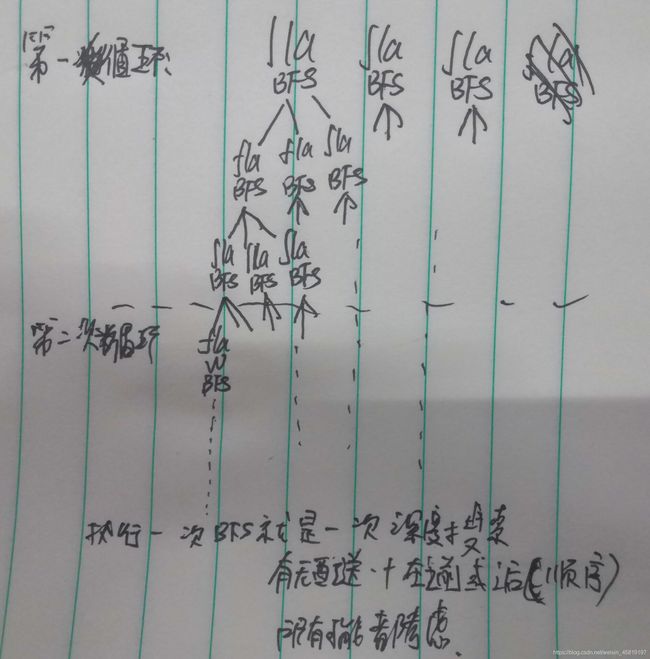
4.思考用bfs的想法,实现实际是dfs.
bfs void(){ rep(i,1,q){
fla =1 bfs() fla()0;
}
rep(i,1,q){
w[i]=1; flg[i]=0; bfs; w[i]=0; flg[i]=1;
} }
多理解理解。
ps: 2号代码(用的是动态规划和二进制,想法很新颖)下次一定(doge);
牛客网:送外卖2 题意
n个点,m条有向边,q个外卖点。
q个外卖点信息 卖家位置,顾客位置,卖家做好的时间,顾客要求的时间送达
不管时间,问能送达的最大的外卖的点数。
1-------------------代码如下:
使用BFS解决
2020.11.11 优化后的代码
由割点(tarja算法)的启发,对dfs有了深刻的见解。
自己写的,害,dfs太爱了
下面为别人代码。
#include
//cout<
sum=max(num,sum);
//第一个for循环 完成快递员取到一些外卖
//三个主要步骤fla[i]=1 bfs fla[i]=0. 时间复杂度嘛q<=10,算友好
//而且先后顺序也安排好了,如:可送第 1,3,4配送需求,位置变换(3,1,4...)也可以实现。
// 如果i=1了,含第0号配送需求且第1个完成的可能性全都考虑完了。这就是这个for循环的含义.
for(int i=0;i<q;i++){
if(flg[i]||w[i]) continue;//
int ts=max(t+a[s][d[i].u],d[i].t1);
flg[i]=1;
//目的:缩短时间.有些配送需求明显超时或到达不了,不执行bfs,缩短时间.
int r=d[i].t2;
for(int j=0;j<q;j++){
if(d[j].t2<r&&flg[j]==1){
r=d[j].t2;
}
}
if(ts<=r)
bfs(ts,num,d[i].u);
flg[i]=0;
//flg[] 很多状态 一旦变了状态(由flg,w数组,确定状态)就是下一个状态,那么BFS
//BFS后 回到原来状态
}
//第二个循环 完成快递员将外卖送到用户手中. 思想同上一个for循环.
//两个分立又关联的for循环,怎么完成任务呢:送第 1,3,4配送需求,一种情况两个for循环先后执行.
for(int i=0;i<q;i++){
if(w[i]||!flg[i]) continue;
if(t+a[s][d[i].v]<=d[i].t2){
w[i]=1;
flg[i]=0;
bfs(t+a[s][d[i].v],num+1,d[i].v);
w[i]=0;
flg[i]=1;
}
}
return ;
}
int main (){
cin>>n>>m>>q;
int u,v,value;
memset(a,10000,sizeof(a));
for(int i=1;i<=100;i++) a[i][i]=0;
for(int i=1;i<=m;i++){
u=read();v=read(); value=read();
a[u][v]=min(value,a[u][v]);
}
cout<<a[1][4]<<" "<<a[3][1]<<endl<<endl;
//flyod
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
for(int k=1;k<=n;k++){
if(a[j][k]>a[j][i]+a[i][k])
a[j][k]=a[j][i]+a[i][k];
}
}
}
//cout<
for(int i=0;i<q;i++){
d[i].u=read();d[i].v=read();
d[i].t1=read();d[i].t2=read();
}
bfs(0,0,1);
cout<<sum<<endl;
}
2--------------------代码如下:
使用动态规划解决:
#include
for(int k=0;k<q;k++){
if(digit[i][k]==2) num++;
}
ans=max(ans,num);
}
}
}
cout<<ans<<endl;
return 0;
}