拓扑排序-信息学奥赛

拓扑排序

制作人：（CwinSpider）

一、前置知识

• 图的基本概念
• 深度优先搜索（DFS）和广度优先搜索（BFS）算法
• 队列和栈的基本操作

二、知识讲解

1. 什么是拓扑排序？

​ 拓扑排序是一种对有向无环图（DAG）进行排序的算法。拓扑排序的结果是一个有序的顶点列表，其中每个顶点只出现一次，且满足：若存在一条从顶点A到顶点B的边，那么在排序结果中，顶点A出现在顶点B的前面。

​ 拓扑排序算法主要包括以下几个步骤：

1. 找到所有入度为0的顶点，并将它们放入一个队列中。
2. 对于队列中的每个顶点，将其出度的边删除，并将出度变为0的相邻顶点入队。
3. 重复步骤2直到队列为空，或所有顶点都已经被处理过。

2. 拓扑排序的实现

​ 我们可以使用邻接表来表示有向无环图，并使用一个数组 $indegree[]$ 来记录每个顶点的入度。具体实现步骤如下：

2.1 数据准备

#include 
#include 
#include 
using namespace std;

const int MAXN = 10010;
vector<int> G[MAXN];  // 邻接表
int indegree[MAXN];   // 记录每个顶点的入度

备注：数据准备阶段，可以使用邻接表来距离图中顶点的指向边；另外使用一维数组indegree来存放顶点的入度数量。

2.2 主函数

int main() {
    int n, m;
    cin >> n >> m;

    // 读入有向图
    for (int i = 0; i < m; i++) {
        int u, v;
        cin >> u >> v;
        G[u].push_back(v);
        indegree[v]++;
    }

    if (topological_sort(n)) {
        // 输出拓扑排序的结果
        for (int i = 1; i <= n; i++) {
            cout << i << " ";
        }
        cout << endl;
    } else {
        cout << "存在环路，排序失败！" << endl;
    }

    return 0;
}

备注：a.读入每个顶点的指出边存放到 邻接表 中，b.调用拓扑排序函数，根据 函数的返回值 来确定是否构成有 向无环图，如果可以则输出每个顶点DAG后的顺序，否则处理存在 环路 的情况。

2.3 核心代码

bool topological_sort(int n) {
    queue<int> q;     // 存放入度为0的顶点
    for (int i = 1; i <= n; i++) {
        if (indegree[i] == 0) {
            q.push(i);
        }
    }
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        for (auto v : G[u]) {
            indegree[v]--;
            if (indegree[v] == 0) {
                q.push(v);
            }
        }
    }
    for (int i = 1; i <= n; i++) {
        if (indegree[i] != 0) {
            return false;  // 存在环路，排序失败
        }
    }
    return true;  // 排序成功
}

备注：核心代码的流程，a.利用队列来进行层序遍历（BFS的特点就是可以在当前结点遍历前确定好上一层父节点的所有信息）。b.查找所有顶点入度为 $0$ 的顶点入队（入度为 $0$ 代表着什么？代表着优先级高哇！没有结点指向它，说明它不需要完成前置任务。）。c.按照队列存放的结点 $x$ 逐个遍历，遍历的过程中追溯每个结点指出的边对应的结点 $y$ ，将该节点入度值减一（为什么减一？现在已经到达了 $x$ 结点工作了，如果 $x$ 结点对应的 $y$ 任务做完，那么 $x$ $⟶$$y$ 这条边就可以删除了），删除后立刻判断该结点 $y$ 的入度是否为 $0$，如果是说明该结点也成为了没有前置任务的点，可以加入到队列中。重复执行步骤 c ，直到所有结点从队列中出队，此时已完成拓扑排序（DAG）。d.循环处理后的入度数组 $indegree[]$ 如果还存在入度值不等于 $0$ 的结点，说明存在有向环图，不适合用该算法处理，否则为有向无环图。

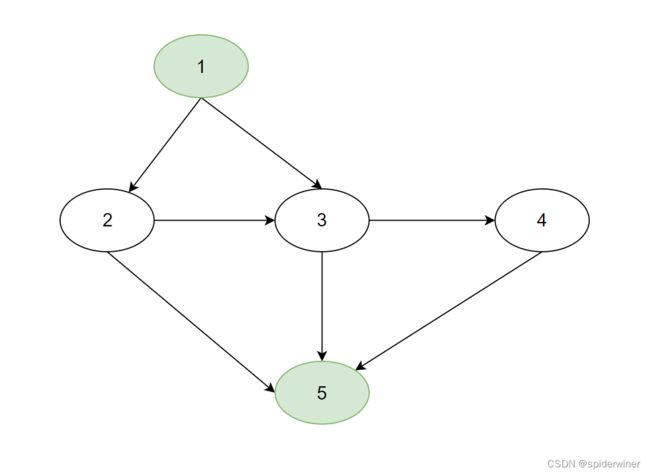
看一组图+视频来解释DAG的运行过程：

a.以下是不是有向无环图？

是的，因为所有结点符合不存在环图，且是有向图。

---

b.接下来我们来观看拓扑排序的过程（[视频]，由于GIF图太模糊）。

拓扑排序的动图展示

3. 拓扑排序的应用

​ 拓扑排序经常用于解决任务调度问题，例如在编译器中，需要对源代码进行编译，但是源代码之间存在依赖关系，即某些 源代码 必须先被 编译 才能 编译其他源代码 。这个问题可以抽象成一个有向无环图，其中每个源代码是一个顶点，源代码之间的依赖关系是有向边。在这个图上进行拓扑排序，就可以得到源代码的编译顺序。

4. 拓扑排序的复杂度分析

​ 拓扑排序的时间复杂度为$O(V+E)$，其中 $V$ 和 $E$ 分别为图的顶点数和边数。因为需要遍历每个顶点和每条边，所以时间复杂度与图的大小成线性关系。

三、课堂练习题

课堂练习（一）

B3644 【模板】拓扑排序 / 家谱树 普及-

题目描述

​ 有个人的家族很大，辈分关系很混乱，请你帮整理一下这种关系。给出每个人的后代的信息。输出一个序列，使得每个人的后辈都比那个人后列出。

输入格式

​ 第 $1$ 行一个整数 $N$（$1\le N\le 100$），表示家族的人数。接下来 $N$ 行，第 $i$ 行描述第 $i$ 个人的后代编号 $a_{i,j}$，表示 $a_{i,j}$ 是 $i$ 的后代。每行最后是 $0$ 表示描述完毕。

输出格式

​ 输出一个序列，使得每个人的后辈都比那个人后列出。如果有多种不同的序列，输出任意一种即可。

样例输入

5
0
4 5 1 0
1 0
5 3 0
3 0

样例输出

2 4 5 3 1

如下图所示（本题抽象后的图形）

AC_Code

#include 
using namespace std;

// B3644 【模板】拓扑排序 / 家谱树
const int mx = 105;
vector<int> vt[mx]; // 邻接表
int ind[mx];        // 入度数组
vector<int> ans;    // 存放DAG后的顶点顺序
int n;

void DAG()
{
    // a.将入度为0的点加入到队列中
    queue<int> q;
    for (int i = 1; i <= n; i++)
    {
        if (ind[i] == 0)
        {
            q.push(i);
            ans.push_back(i);
        }
    }
    // b.使用队列进行层序遍历
    while (q.size())
    {
        // b.a 父节点fa的每一条连接表对应的子节点son
        int fa = q.front();
        q.pop();
        for (int x = 0; x < vt[fa].size(); x++)
        {
            int son = vt[fa][x];
            // b.b 将此连接边删除，并判断已完成前置任务，如果是入队
            ind[son]--;
            if (ind[son] == 0)
            {
                q.push(son);
                ans.push_back(son);
            }
        }
    }
    // c.因为题目说明了必须是有向无环图，那么不用再判断是否是【有向无环图】了
}

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        int tmp;
        // a.读入i顶点的连接边存放到邻接表
        while (cin >> tmp && tmp)
        {
            vt[i].push_back(tmp);
            ind[tmp]++; //注意入度的是点i连接的点tmp，tmp入度+1
        }
    }
    DAG(); // b.拓扑排序
    // c.按顺序输出结果
    for (int i = 0; i < ans.size(); i++)
    {
        cout << ans[i] << " ";
    }
    system("pause");
    return 0;
}
/*
输入样例：
5
0
4 5 1 0
1 0
5 3 0
3 0
输出样例：
2 4 5 3 1
*/

课堂练习（二）

P1807 最长路 普及/提高-

本题注意包含（动态规划思想）

题目描述

​ 设 $G$ 为有 $n$ 个顶点的带权有向无环图，$G$ 中各顶点的编号为 $1$ 到 $n$，请设计算法，计算图 $G$ 中 $1,n$ 间的最长路径。

输入格式

​ 输入的第一行有两个整数，分别代表图的点数 $n$ 和边数 $m$。

​ 第 $2$ 到第 $(m+1)$ 行，每行 $3$ 个整数 $u,v,w$（$u<v$），代表存在一条从 $u$ 到 $v$ 边权为 $w$ 的边。

输出格式

​ 输出一行一个整数，代表 $1$ 到 $n$ 的最长路。

​ 若 $1$ 无法到达 $n$，请输出 $-1$。

提示

【数据规模与约定】

• 对于 $20\%$的数据，$n\le 100$，$m\le 10^3$。
• 对于 $40\%$ 的数据，$n\le 10^3$，$m\le 10^4$。
• 对于 $100\%$ 的数据，$1\le n\le 1500$，$0\le m\le 5\times 10^4$，$1\le u,v\le n$，$-10^5\le w\le 10^5$。

样例输入

2 1
1 2 1

样例输出

1

新增数据点

5 6
1 2 1
2 3 2
3 5 3
1 4 1
4 5 2
3 4 1

输出

3

下图给出新增数据点的连接图

可以从图中看出，1->5的最短路径为1->4->5，路径长度为1+2=3。

本题注意坑点：

1. 题目已经保证了点 1 是起点，而且不会出现环，满足了拓扑排序的要求。但是题目**却没有保证只有点 1 是如度为 0 的点。**所以要判断其他入度为 0 的点 $x$，按照以往的操作我们是将该点 $x$ 加入到队列中，但这次不能这么操作，为什么呢？

2. 因为该点 $x$ 是本身是无法到达的点，且不可能延伸其他地方，如果入队了会导致个别点，甚至所有点的答案错误。那么我们是置于它不管吗？还是错！为什么错？

3. 如果不管，那么延伸出来的点的入度永远大于0，可能会导致永远无法到达终点！如何解决呢？

4. 正确的做法，将这些点 $x$ 所能延伸的点 $y$ 入度 减 1，注意！如果这些延伸的点 $y$ 减 1 后还是为0，做上述同样的处理。

5. 至于一个点的最长路的转移方程就是：

   $min(入度1+对应边，入度2+对应的边...入度n+对应的边)$

AC_Code

#include  //万能头文件
using namespace std;     // 标准命名空间

/*
题目类型：广搜、拓扑排序、图
题目名称：P1807 最长路
题目难度：B++
基本思路：
1.设置结构体终点to,权值val。
2.使用邻接表建立起点->终点、权值的关系。
3.队列queue存放待扩展结点。
4.从点1开始广搜，在处理点n之前，必须把n之前连接n的点k处理好（存放最短路径值）。
5.存放队列扩展的最短长度。
*/

const int nmax = 1505;
const int mmax = 1e4 + 5;
struct node
{
    int to, val; // 终点和权值
};
queue<int> q;           // 队列广搜
vector<node> vt[nmax];  // 邻接表
int ind[nmax], f[nmax]; // 入度，结果(动规)

int main() // 主程序入口
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= m; i++)
    {
        int x, y, v;
        cin >> x >> y >> v;
        ind[y]++;                      // 入度+1
        vt[x].push_back((node){y, v}); // 建立邻接表
    }
    // a.初始化（题目要求算出1~n顶点最短路径，确定了开头和结尾，所以从顶点2开始预处理
    for (int i = 2; i <= n; i++)
    {
        f[i] = -1e9;
        if (!ind[i]) // 入度为0的顶点入队。
            q.push(i);
    }
    // b.处理废弃的点(队列中)，将其结点连接的边做(删边)操作。
    while (!q.empty())
    {
        int x = q.front(); // 取点删边
        q.pop();
        for (int i = 0; i < vt[x].size(); i++)
        {
            int next = vt[x][i].to;
            if (!--ind[next])
                q.push(next); // 如果删边的点已经，入度为0将结点加入队列继续处理（废弃）
        }
    }
    // c.开始处理1~n的正常点，比对路径最大值
    q.push(1);
    while (!q.empty())
    {
        int x = q.front();
        q.pop();
        for (int i = 0; i < vt[x].size(); i++)
        {
            int y = vt[x][i].to;    // 终点
            int val = vt[x][i].val; // 权值
            // c.a 状态转移
            if (f[y] < f[x] + val)
                f[y] = f[x] + val;
            // c.b 入度为0的点持续入队（广搜）
            if (!--ind[y])
                q.push(y);
        }
    }
    // d.终点n经过处理后所存储的状态fn判断是否为更新后的值
    if (f[n] == -1e9)
        cout << -1 << endl;
    else
        cout << f[n] << endl;
    return 0;
}

/*
【样例输入】
2 1
1 2 1
【样例输出】
1
*/

四、精选例题

例题1

​ P4017 最大食物链计数 普及/提高-（拓扑排序）

题目背景

​ 你知道食物链吗？Delia 生物考试的时候，数食物链条数的题目全都错了，因为她总是重复数了几条或漏掉了几条。于是她来就来求助你，然而你也不会啊！写一个程序来帮帮她吧。

题目描述

​ 给你一个食物网，你要求出这个食物网中最大食物链的数量。

​ （这里的“最大食物链”，指的是生物学意义上的食物链，即最左端是不会捕食其他生物的生产者，最右端是不会被其他生物捕食的消费者。）

​ Delia 非常急，所以你只有 $1$ 秒的时间。

​ 由于这个结果可能过大，你只需要输出总数模上 $80112002$ 的结果。

输入格式

​ 第一行，两个正整数 $n、m$，表示生物种类 $n$ 和吃与被吃的关系数 $m$。

​ 接下来 $m$ 行，每行两个正整数，表示被吃的生物A和吃A的生物B。

输出格式

​ 一行一个整数，为最大食物链数量模上 $80112002$ 的结果。

样例输入 #1

5 7
1 2
1 3
2 3
3 5
2 5
4 5
3 4

样例输出 #1

5

抽象成图所示

提示和补充说明

各测试点满足以下约定：

$n\le 5000,m\le 500000$

【补充说明】

给出解题思路（仅作参考）

这道题目是一道 DAG 上的动态规划问题（DP+DAG），需要用到 DAG 的拓扑排序来解决。

​ 首先，我们可以根据题目中的要求， 将 DAG 中的点按照它们的拓扑序排列。 这个过程可以使用拓扑排序来实现。在拓扑排序的过程中，我们需要用到一个队列，将入度为 0 的点加入队列中，并顺序遍历它们的后继节点，更新它们的状态。

​ 在本题中，我们需要求出从 起点到终点的最长路径条数。 为了求出最长路径条数，我们需要 对每个点记录一下从起点到该点的最长路径条数。 状态转移方程推导过程：设 $f(i)$ 表示从起点到点 $i$ 的最长路径条数。因为该 DAG 是有向无环图，所以我们可以使用拓扑排序的顺序，从起点开始逐个遍历它们的后继节点 $j$，并更新最长路径条数：$f(j)=f(j)+f(i)$。

​ 具体地，我们可以在拓扑排序中，每次从队列中弹出一个点 $i$ 后，计算从起点到 $i$ 的最长路径条数 $f(i)$，然后遍历 $i$ 的所有后继节点 $j$，并更新 $f(j)$。如果 $j$ 的入度为 0，说明 $j$ 的前置任务已经完成，可以将 $j$ 加入队列中。

​ 最后，我们只需要统计所有出度为 0 的点的最长路径条数之和，即为所求的结果。

​ 需要注意的是，由于本题中的最长路径条数可能非常大，需要使用取模的方式来避免溢出。此外，如果 DAG 中存在环路，就无法进行拓扑排序，也就无法求出最长路径条数，此时需要特别处理。

以上就是本题的主要思路和实现方法。

数据中不会出现环，满足生物学的要求。

#include  //万能头文件
using namespace std;     // 标准命名空间

/*
题目类型： DAG拓扑排序、邻接表、队列、图
题目名称： P4017 最大食物链计数
题目难度：B+
*/
const int mod = 80112002;
const int mx = 500005;
const int mx2 = 5005;
int ind[mx2], outd[mx2], f[mx2];
vector<int> edge[mx2];
queue<int> q;

void DAG()
{
    while (!q.empty())
    {
        int x = q.front();
        q.pop();
        for (int i = 0; i < edge[x].size(); i++)
        {
            int y = edge[x][i];
            f[y] = (f[y] + f[x]) % mod;
            ind[y]--; // 删边
            if (ind[y] == 0)
                q.push(y); // 终点y已经没有入度（理解为已经做好准备工作了，可以待搜加入队列）
        }
    }
}

int main()
{ // 主程序入口
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= m; i++)
    {
        int x, y;
        cin >> x >> y;
        outd[x]++; // 点的入度和出度+1
        ind[y]++;
        edge[x].push_back(y); // 邻接表
    }
    for (int i = 1; i <= n; i++)
    {
        if (ind[i] == 0)
        {
            q.push(i); // 入度为 0 的点为起点（可以作为第一层搜索的对象）
            f[i] = 1;  // 所有点初始化长度为1（本身）
        }
    }
    DAG(); // 拓扑排序
    int ans = 0;
    for (int i = 1; i <= n; i++)
    {
        if (outd[i] == 0)
            ans = (ans + f[i]) % mod; //上述例子中只有顶点5的出度为0，f[5]=5，结果为5.
    }
    cout << ans << endl;
    return 0;
}

批注：有需要的老师可以自行画图带着学生去理解，很简单不做图了。

例题2

​ P1113 杂务 普及/提高-（有向无环图）

题目描述

​ John的农场在给奶牛挤奶前有很多杂务要完成，每一项杂务都需要一定的时间来完成它。比如：他们要将奶牛集合起来，将他们赶进牛棚，为奶牛清洗乳房以及一些其它工作。尽早将所有杂务完成是必要的，因为这样才有更多时间挤出更多的牛奶。当然，有些杂务必须在另一些杂务完成的情况下才能进行。比如：只有将奶牛赶进牛棚才能开始为它清洗乳房，还有在未给奶牛清洗乳房之前不能挤奶。我们把这些工作称为完成本项工作的准备工作。至少有一项杂务不要求有准备工作，这个可以最早着手完成的工作，标记为杂务$1$。John有需要完成的$n$个杂务的清单，并且这份清单是有一定顺序的，杂务$k(k>1)$的准备工作只可能在杂务$1$至$k-1$中。

​ 写一个程序从$1$到$n$读入每个杂务的工作说明。计算出所有杂务都被完成的最短时间。当然互相没有关系的杂务可以同时工作，并且，你可以假定John的农场有足够多的工人来同时完成任意多项任务。

输入格式

​ 第1行：一个整数$n$，必须完成的杂务的数目($3\le n\le 10,000$)；

​ 第$2$至$(n+1)$行： 共有$n$行，每行有一些用$1$个空格隔开的整数，分别表示：

​ * 工作序号($1$至$n$,在输入文件中是有序的)；

​ * 完成工作所需要的时间$len(1\le len\le 100)$；

​ * 一些必须完成的准备工作，总数不超过$100$个，由一个数字$0$结束。有些杂务没有需要准备的工作只描述一个单独的$0$，整个输入文件中不会出现多余的空格。

输出格式

​ 一个整数，表示完成所有杂务所需的最短时间。

样例输入

7
1 5 0
2 2 1 0
3 3 2 0
4 6 1 0
5 1 2 4 0
6 8 2 4 0
7 4 3 5 6 0

样例输出

23

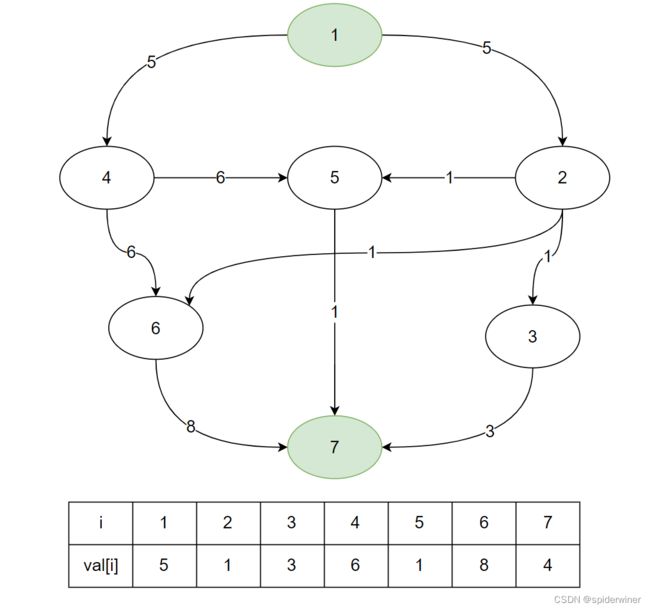
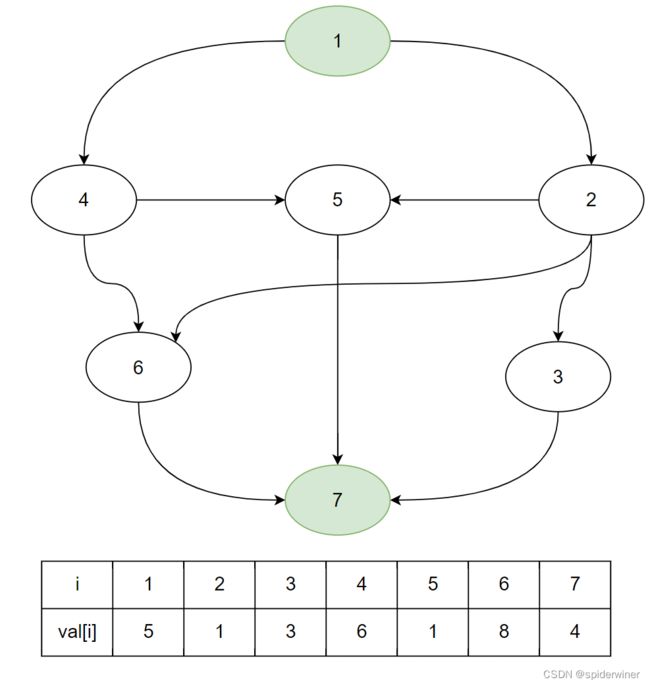
粗略的图，凑合的看

开个玩笑，放上 整容后的图片 正经图

---

做题思路：

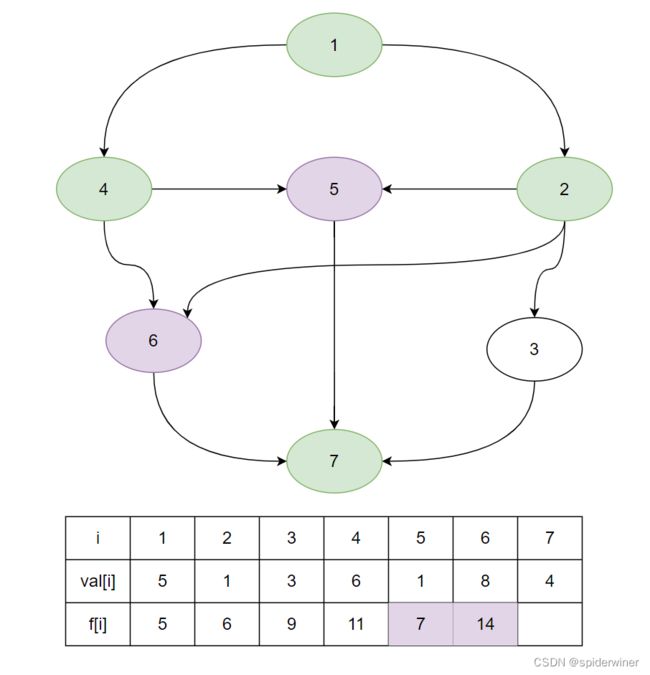
​ 利用数组 $f[i]$ 来维护完成任务 $i$ 所记录的最短时间，然后在 $BFS$ 的过程中去更新 $f[i]$ 的值。

​ 看下来来观察 $f[i]$ 数组维护的过程。

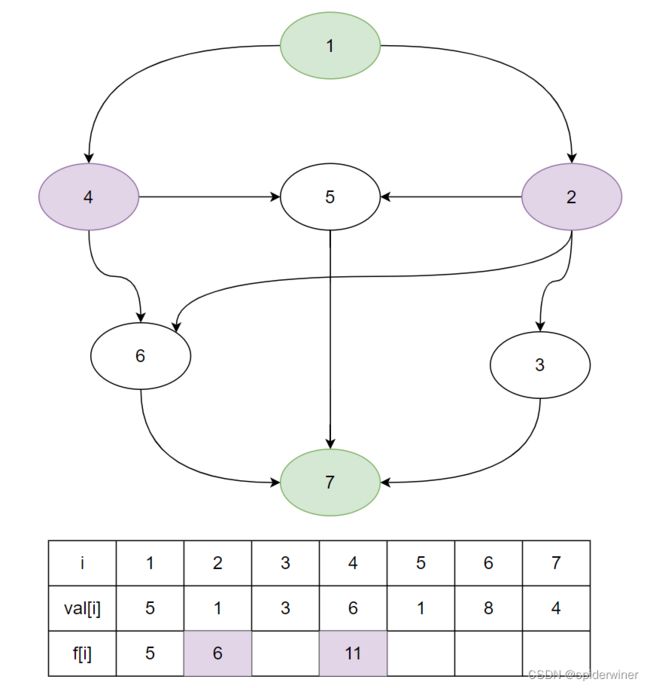
如上图所示，顶点 $1$ 的 $f[1]$ 的值会更新为本身任务所做的时间 $5，f[1]=5$，因为入度值为 $0$ 的点先做，没有任务前置任务。

---

接下来观看，顶点 $1$ 所连接的两条边的顶点 $4、2$ 这两个点的最短时间值的变化 $f[4]、f[2]$。

由于顶点 $4、2$ 这两个点只需要前置的任务 $1$ 就可以开始工作了，所以他们只在 $f[1]$ 值上去更新。

$f[2]=f[1]+val[2]=5+1=6$

$f[4]=f[1]+val[2]=5+6=11$

---

接下来观看，顶点 $2$ 所连接的两条边的顶点 $6、3、5$ ，这三个点的最短时间值的变化 $f[6]、f[3]、f[5]$。

​ 顶点 $2$ 所能延伸的顶点是 $3、5、6$ ，这三个点，所虽然还有其他前置任务但是最先找到他们的任务是 $2$ ，所以先由顶点 $2$ 来先更新顶点 $3、5、6$ 这三个点的最短完成任务时间。

$f[3]=f[2]+val[3]=6+3=9$

$f[5]=f[2]+val[5]=6+1=7$

$f[6]=f[2]+val[6]=6+8=14$

---

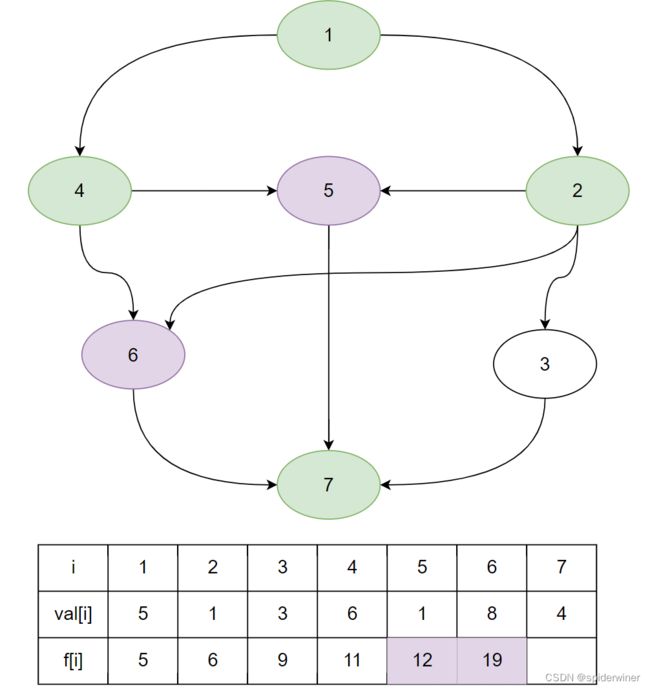
接下来观看，顶点 $4$ 所连接的两条边的顶点 $5、6$，这三个点的最短时间值的变化 $f[5]、f[6]$。

​ 顶点 $4$ 所能延伸的顶点是 $5、6$ ，这两个点，虽然还有其他前置任务但是顶点 $4$ 是第二个找到他们的。为什么越更新得所需要得时间就越长啊？？？（思考一下）此时结点 $5、6$ 不再是第一次被访问了（通俗一点：就是前置任务有多个，现在要找出前置当中做合计时长最长的那个作为本次任务的最短时间，为什么呢？因为我们任务是可以同时进行的呀！！！我们就可以找合计完成时间最长的任务来计算即可包括了所有的前置任务的完成时间），结论：找出完成当前任务 $x$ 的前置任务 $y$ + 完成任务 $x$ 的时间的最大值。

​ 直接上状态转移方程：$f[x]=max(f[x],f[y]+val[x])$

​ 超级简单的有没有？

$f[5]=max(f[5],f[4]+val[5]=max(7,12)=12$

$f[6]=max(f[6],f[4]+val[6])=max(14,19)=19$

---

接下来观看，顶点 $3$ 所连接的一条边的顶点 $7$，这个点的最短时间值的变化 $f[7]$。

​ 顶点 $3$ 所能延伸的顶点是 $7$ ，这个点算是第一次被连接所以首次更新很简单，就只能来自于任务 $3$ 完成的最短时间上加本身任务 $7$ 完成的时间就为任务 $7$ 的最短时间。

$f[7]=f[3]+val[7]=9+4=13$

---

接下来观看，顶点 $5$ 所连接的一条边的顶点 $7$，这个点的最短时间值的变化 $f[7]$。

​ 顶点 $5$ 所能延伸的顶点是 $7$ ，这个点是第二次被连接所以要进行比对找出最大值，当前任务 $7$ 所记录的最短完成任务时间 $f[7]=13$，与任务 $5$ 所记录的最短完成任务时间 $f[5]$ + 完成任务7的任务时间 $val[7]$ 进行对比。

​ $f[7]=max(f[7],f[5]+val[7])=max(13,16)=16$

同学们观察上图，还有什么点没有搜索过呀？

剩余点（$6、7$）

$f[7]=max(f[7],f[6]+val[7])=max(16,19+4)=23$

任务 $7$ 所记录的时间被更新！

---

由于点 $7$ 没有延伸点，点 $n=7$ 所记录的就是答案！！！(完成 $1-n$ )所需的最短时间为 $f[7]=23$

思路清晰 + 理解透彻，代码就水到渠成！！！

AC_Code

#include  //万能头文件
using namespace std;     // 标准命名空间

/*
题目类型：图、邻接表拓扑排序
题目名称：P1113 杂务
题目难度：B++
*/

inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9')
    {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9')
    {
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}
const int mx = 100005;
vector<int> edge[mx];
queue<int> q;
int ind[mx], f[mx], a[mx]; // ind--入度，f--答案，a--时间

int main()
{ // 主程序入口
    int n = read();
    for (int i = 1; i <= n; i++)
    {
        int x = read();
        a[i] = read();
        while (int y = read())
        {
            if (!y)
                break;            // 0结束
            edge[y].push_back(x); // 注意建边的起点是y终点是x
            ind[x]++;             // 入度x边数量+1
        }
    }
    // 步骤一:初始化队列，将入度为 0 的节点放入队列。
    for (int i = 1; i <= n; i++)
    {
        if (ind[i] == 0)
        {
            q.push(i);
            f[i] = a[i];
        }
    }
    while (!q.empty())
    {
        int y = q.front(); // 入度为0的优先
        q.pop();
        // 步骤二：取出队首，遍历其出边，将能够到达的点入度减一，同时维护答案数组。
        for (int i = 0; i < edge[y].size(); i++)
        { // 取出点x前往的点u
            int x = edge[y][i];
            ind[x]--;
            // 步骤三： 若在此时一个点的入度变为 1，那么将其加入队列。
            if (ind[x] == 0)
                q.push(x);
            f[x] = max(f[x], f[y] + a[x]); // 利用动态规划维护的f[u]比对最大值
        }
    }
    int ans = 0;
    for (int i = 1; i <= n; i++)
    {
        ans = max(ans, f[i]);
    }
    cout << ans << endl;
    system("pause");
    return 0;
}

/*
【样例输入】
7
1 5 0
2 2 1 0
3 3 2 0
4 6 1 0
5 1 2 4 0
6 8 2 4 0
7 4 3 5 6 0
【样例输出】
23
*/

五、总结

​ 本节课讲解了拓扑排序的概念、实现、应用以及复杂度分析。

​ 拓扑排序是一种对有向无环图进行排序的算法，其应用范围非常广泛，例如任务调度、编译器等领域。

​ 拓扑排序的实现需要使用邻接表和入度数组，时间复杂度为O(V+E)。

​ 同学们可以通过练习题和例题来加深对拓扑排序算法的理解和掌握。

六、课后作业

以下是两道拓扑排序相关的课后练习题：

1. P2661 [NOIP2015 提高组] 信息传递 普及/提高-
2. P8893 「UOI-R1」智能推荐 普及/提高-

希望同学们能够认真完成课后作业，加深对拓扑排序算法的理解和掌握。