单用户MIMO系统（二）：信道信息在发端未知

单用户MIMO系统（二）：信道信息在发端未知

关键词

MIMO，单用户，信道容量，MMSE-SIC，Matlab实现

基本介绍

本文介绍了单用户MIMO系统在发端不知道信道状态信息时的系统传输速率以及相应的接收机结构，并且给出了对应的Matlab实现。针对MIMO的接收机结构，本文重点论述了MMSE-SIC译码器的性质。

考虑图1所示的单用户MIMO系统，发射机配有$N_{\text{t}}$条射频链路，接收机配置有$N_{\text{r}}$条射频链路，无线信道可以用矩阵$\text{H}\in {\mathbb{C}}^{N_{\text{r}}\times N_{\text{t}}}$表示。接收机接收到的信号向量为：$$\text{y}=\text{H}\text{s}+\text{n},$$其中$\text{s}\in {\mathbb{C}}^{N_{\text{t}}\times 1}$表示传输的信号向量， $\text{n}\sim \mathcal{C}\mathcal{N}\left(0,{\sigma }^2{\text{I}}_{N_{\text{r}}}\right)$表示接收侧加性噪声，系统传输速率可以表示为[1]$$\mathcal{R}=\log \det \left({\text{I}}_{N_{\text{r}}}+\frac{1}{{\sigma }^2}\text{H}\mathbf{\Phi }{\text{H}}^{†}\right),$$其中$\mathbf{\Phi }=\mathbb{E}\left\{\text{s}{\text{s}}^{†}\right\}$表示发射信号的协方差矩阵，$\mathrm{T}\mathrm{r}\left(\mathbf{\Phi }\right)$表示传输功率。

图1：单用户MIMO传输系统框图

由于此时发送方无法利用$\text{H}$来对协方差矩阵$\mathbf{\Phi }$进行优化。此时，发送方只能选择将功率平均分配每个数据流，并且将单位矩阵${\text{I}}_{N_{\text{t}}}$作为预编码矩阵。综上所述，此时采用的协方差矩阵为$\mathbf{\Phi }=\sqrt{P/N_{\text{t}}}{\text{I}}_{N_{\text{t}}}$，其中$P>0$表示传输功率。因此，此时的传输速率为$$\mathcal{R}=\log \det \left({\text{I}}_{N_{\text{r}}}+\frac{P}{N_{\text{t}}{\sigma }^2}\text{H}{\text{H}}^{†}\right).$$注意，由于信道信息$\text{H}$在发送方不可知，信道容量（最大传输速率）是不可达的。

接下来，考虑接收机的结构。此时，接收端收到的信号为$$\text{y}=\text{H}\text{s}+\text{n}.$$为了使得传输速率达到此时的最大可达传输速率$\mathcal{R}=\log \det \left({\text{I}}_{N_{\text{r}}}+\frac{P}{N_{\text{t}}{\sigma }^2}\text{H}{\text{H}}^{†}\right)$，接收端需要将接收到的信号向量$\text{y}$直接送入译码器，对发送的数据流进行联合译码（joint decoding），这个过程具有指数复杂度。前文提及，当发送方与接收方同时知道信道$\text{H}$时，接收方与发送方分别利用信道矩阵的左右奇异矩阵进行滤波和预编码就可以将信道$\text{H}$分解为几个并行子信道，接下来对这些子信道进行并行译码即可。并行译码的复杂度远低于联合译码的复杂度。当信道信息在发送方未知的时候，发送方无法进行相应的预编码使得整个信道最终可以分解为若干个并行子信道。直观上来看，此时接收端必须采用联合译码。但是，可以有复杂度更低的译码方式来使得系统传输速率为最大可达传输速率。

记$\text{s}={\left[s_1,\cdots ,s_{N_{\text{t}}}\right]}^{⊺}$，其中$s_i$表示传输的第$i$条数据流（或者第$i$个符号），满足$\mathbb{E}\left\{s_i{s}_i^{†}\right\}=\frac{P}{N_{\text{t}}}$。因此，接收到的信号$\text{y}$可以写为$$\text{y}={\text{y}}_1={\text{h}}_1{s}_1+\sum _{i=2}^{N_{\text{t}}}{\text{h}}_i{s}_i+\text{n},$$其中${\text{h}}_i\in {\mathbb{C}}^{N_{\text{r}}\times 1}$表示信道矩阵$\text{H}$的第$i$列。先从接收到的信号$\text{y}$中恢复出第1条数据流$s_1$中的信息，此时可以将${\text{z}}_1={\sum }_{i=2}^{N_{\text{t}}}{\text{h}}_i{s}_i+\text{n}$视为干扰，其中$\text{n}\sim \mathcal{C}\mathcal{N}\left(\text{0},{\sigma }^2{\text{I}}_{N_{\text{r}}}\right)$表示加性白高斯噪声，${\sum }_{i=2}^{N_{\text{t}}}{\text{h}}_i{s}_i$表示数据流之间的流间干扰。为了恢复数据流$s_1$中的信息，可以先将接收信号通过滤波器${\text{c}}_1\in {\mathbb{C}}^{N_{\text{r}}\times 1}$，再将滤波器的输出送入译码器。接下来，需要对滤波器进行设计。具体来讲，滤波器的输出为：$$r_1={\text{c}}_1^{†}{\text{y}}_1=\left({\text{c}}_1^{†}{\text{h}}_1\right)s_1+{\text{c}}_1^{†}{\text{z}}_1=\left({\text{c}}_1^{†}{\text{h}}_1\right)s_1+{\text{c}}_1^{†}\left(\sum _{i=2}^{N_{\text{t}}}{\text{h}}_i{s}_i+\text{n}\right).$$由于信道最大传输速率的实现需要输入的信号服从高斯分布，因此$s_i\sim \mathcal{C}\mathcal{N}\left(0,\sqrt{\frac{P}{N_{\text{t}}}}\right)$，由此可知干扰项${\text{z}}_1$服从复高斯分布，协方差矩阵为$$\mathbb{E}\left\{{\text{z}}_1{\text{z}}_1^{†}\right\}={\sigma }^2{\text{I}}_{N_{\text{r}}}+\frac{P}{N_{\text{t}}}\sum _{i=2}^{N_{\text{t}}}{\text{h}}_i{\text{h}}_i^{†}={\text{K}}_1\succ \text{0}.$$显然，${\text{K}}_1$是个正定矩阵。$r_1=\left({\text{c}}_1^{†}{\text{h}}_1\right)s_1+{\text{c}}_1^{†}{\text{z}}_1$可以视为一个单入单出（single-input single-output, SISO）信道的输出，信道为${\text{c}}_1^{†}{\text{h}}_1$，输入信号为$s_1$，干扰为${\text{c}}_1^{†}{\text{z}}_1$。在这个系统模型中，需要设计的是滤波器向量${\text{c}}_1$。一个直观的设计思路是使得这个信道的信道容量最大，对于一个SISO信道而言，最大化信道容量等价于最大化接收端的信噪比。具体来讲，这个信道的接收信噪比可以表示为$${\gamma }_1=\frac{P}{N_{\text{t}}}\frac{{\left|{\text{c}}_1^{†}{\text{h}}_1\right|}^2}{\mathbb{E}\left\{{\left|{\text{c}}_1^{†}{\text{z}}_1\right|}^2\right\}}=\frac{P}{N_{\text{t}}}\frac{{\text{c}}_1^{†}{\text{h}}_1{\text{h}}_1^{†}{\text{c}}_1}{{\text{c}}_1^{†}{\text{K}}_1{\text{c}}_1}.$$对应的优化问题可以建模为$${\text{c}}_1^{\star }=\arg \underset{{\text{c}}_1}{\max }\frac{{\text{c}}_1^{†}{\text{h}}_1{\text{h}}_1^{†}{\text{c}}_1}{{\text{c}}_1^{†}{\text{K}}_1{\text{c}}_1}.$$上述问题是一个无约束优化问题，不过目标函数不是关于${\text{c}}_1$的凹函数。为解决上述问题，引入辅助变量${\text{v}}_1={\text{K}}_1^{1/2}{\text{c}}_1$，由此可以得到${\text{c}}_1^{\star }={\text{K}}_1^{-1/2}{\text{v}}_1^{\star }$，其中$${\text{v}}_1^{\star }=\arg \underset{{\text{v}}_1}{\max }\frac{{\text{v}}_1^{†}{\text{K}}_1^{-1/2}{\text{h}}_1{\text{h}}_1^{†}{{\text{K}}_1^{-1/2}}^{†}{\text{v}}_1}{{\text{v}}_1^{†}{\text{K}}_1^{-1/2}{\text{K}}_1{{\text{K}}_1^{-1/2}}^{†}{\text{v}}_1}=\arg \underset{{\text{v}}_1}{\max }{\left|\frac{{\text{v}}_1^{†}}{\Vert {\text{v}}_1\Vert }\left({\text{K}}_1^{-1/2}{\text{h}}_1\right)\right|}^2.$$注意上式的化简过程用到性质“${\text{K}}_1$是个厄尔米特矩阵”，即${\text{K}}_1={\text{K}}_1^{†}$，以及 （ ${\text{K}}_1^a={{\text{K}}_1^a}^{†}$）。上述问题的本质是寻找一个向量，它的方向向量与向量${\text{K}}_1^{-1/2}{\text{h}}_1$的内积的平方最大，显然最优解为${\text{v}}_1^{\star }=c{\text{K}}_1^{-1/2}{\text{h}}_1$，其中$c$是个非0常数。综上所述，${\text{c}}_1^{\star }=c{\text{K}}_1^{-1}{\text{h}}_1$，对应的接收端信噪比为${\gamma }_1=\frac{P}{N_{\text{t}}}{\text{h}}_1^{†}{\text{K}}_1^{-1}{\text{h}}_1$，信道容量为${\mathcal{R}}_1=\log \left(1+\frac{P}{N_{\text{t}}}{\text{h}}_1^{†}{\text{K}}_1^{-1}{\text{h}}_1\right)$。如果将${\text{y}}_1={\text{h}}_1{s}_1+{\text{z}}_1$视为一个简单的MIMO信道模型，1根发送天线，$N_{\text{r}}$条接收天线，相应的信道容量为：$${\mathcal{C}}_1=\log \det \left({\text{I}}_{N_{\text{r}}}+\frac{P}{N_{\text{t}}}{\text{h}}_1{\text{h}}_1^{†}{\text{K}}_1^{-1}\right).$$利用Sylvester行列式等式$\log \det \left(\text{I}+\text{A}\text{B}\right)=\log \det \left(\text{I}+\text{B}\text{A}\right)$，可以得到：$${\mathcal{C}}_1=\log \det \left({\text{I}}_{N_{\text{r}}}+\frac{P}{N_{\text{t}}}{\text{h}}_1{\text{h}}_1^{†}{\text{K}}_1^{-1}\right)=\log \left(1+\frac{P}{N_{\text{t}}}{\text{h}}_1^{†}{\text{K}}_1^{-1}{\text{h}}_1\right)={\mathcal{R}}_1.$$根据信道容量的定义，信道容量等于输入信号与输出信号之间互信息的最大值。用$\mathcal{I}\left(x;y\right)$表示随机变量$x$与$y$的互信息，在高斯输入下（信道容量依赖于高斯输入实现），可以得到${\mathcal{C}}_1=\mathcal{I}\left({\text{y}}_1;s_1\right)$、${\mathcal{R}}_1=\mathcal{I}\left({{\text{c}}_1^{\star }}^{†}{\text{y}}_1;s_1\right)$。有下列关系成立，$$\mathcal{I}\left({\text{y}}_1;s_1\right)={\mathcal{C}}_1={\mathcal{R}}_1=\mathcal{I}\left({{\text{c}}_1^{\star }}^{†}{\text{y}}_1;s_1\right).$$由上式可知，利用${\text{c}}_1^{\star }$进行滤波不会减少输入输出互信息，即利用${\text{c}}_1^{\star }$进行滤波是信息无损的（information lossless）。接下来，从信号检测的角度进一步探究滤波器${\text{c}}_1^{\star }$的性质。对于模型${\text{y}}_1={\text{h}}_1{s}_1+{\text{z}}_1$而言，在接收机采用线性检测器$\text{u}\in {\mathbb{C}}^{N_{\text{r}}\times 1}$，衡量检测器的性能指标为均方误差（mean-square error，MSE），表示为$$\text{MSE}=\mathbb{E}\left\{{\left({\text{u}}^{†}{\text{y}}_1-s_1\right)}^{†}\left({\text{u}}^{†}{\text{y}}_1-s_1\right)\right\},$$其中上式的均值是针对信号$s_1$以及${\text{z}}_1$的随机性而取的。注意$s_1$以及${\text{z}}_1$的均值为0，且这两个随机变量互相独立。将${\text{y}}_1={\text{h}}_1{s}_1+{\text{z}}_1$代入上式，可以得到：$$\begin{array}{rl}\text{MSE}& =\mathbb{E}\left\{{\left({\text{u}}^{†}{\text{y}}_1-s_1\right)}^{†}\left({\text{u}}^{†}{\text{y}}_1-s_1\right)\right\}\\ & =\mathbb{E}\left\{{\left({\text{u}}^{†}{\text{h}}_1{s}_1+{\text{u}}^{†}{\text{z}}_1-s_1\right)}^{†}\left({\text{u}}^{†}{\text{h}}_1{s}_1+{\text{u}}^{†}{\text{z}}_1-s_1\right)\right\}\\ & ={\text{u}}^{†}\left(\frac{P}{N_{\text{t}}}{\text{h}}_1{\text{h}}_1^{†}+{\text{K}}_1\right)\text{u}-\frac{P}{N_{\text{t}}}{\text{u}}^{†}{\text{h}}_1-\frac{P}{N_{\text{t}}}{\text{h}}_1^{†}\text{u}+\frac{P}{N_{\text{t}}}\end{array}.$$检测的目的是希望能设计出使得均方误差最小的检测器，即解决下述问题：$${\text{u}}^{\star }=\arg \underset{\text{u}}{\min }\text{MSE}=\arg \underset{\text{u}}{\min }{\text{u}}^{†}\left(\frac{P}{N_{\text{t}}}{\text{h}}_1{\text{h}}_1^{†}+{\text{K}}_1\right)\text{u}-\frac{P}{N_{\text{t}}}{\text{u}}^{†}{\text{h}}_1-\frac{P}{N_{\text{t}}}{\text{h}}_1^{†}\text{u}.$$上述问题是一个无约束问题，且目标函数是$\text{u}$的凸函数，因此最优解在偏导为$\text{0}$的地方取得[2]，即：${\nabla }_{\text{u}}\text{MSE}=\text{0}$ ，其中${\nabla }_{\text{u}}\text{MSE}$表示函数$\text{MSE}$关于$\text{u}$的共轭复梯度，为$${\nabla }_{\text{u}}\text{MSE}=\left(\frac{P}{N_{\text{t}}}{\text{h}}_1{\text{h}}_1^{†}+{\text{K}}_1\right)\text{u}-\frac{P}{N_{\text{t}}}{\text{h}}_1.$$求解方程${\nabla }_{\text{u}}\text{MSE}=\text{0}$，得到$${\text{u}}^{\star }=\frac{P}{N_{\text{t}}}{\left(\frac{P}{N_{\text{t}}}{\text{h}}_1{\text{h}}_1^{†}+{\text{K}}_1\right)}^{-1}{\text{h}}_1.$$利用矩阵求逆公式${\left(\text{A}+\text{x}{\text{x}}^{†}\right)}^{-1}={\text{A}}^{-1}-\frac{{\text{A}}^{-1}\text{x}{\text{x}}^{†}{\text{A}}^{-1}}{1+{\text{x}}^{†}{\text{A}}^{-1}\text{x}}$，可以得到：$$\begin{array}{rl}{\text{u}}^{\star }& =\frac{P}{N_{\text{t}}}{\left(\frac{P}{N_{\text{t}}}{\text{h}}_1{\text{h}}_1^{†}+{\text{K}}_1\right)}^{-1}{\text{h}}_1=\frac{P}{N_{\text{t}}}\left({\text{K}}_1^{-1}-\frac{{\text{K}}_1^{-1}\frac{P}{N_{\text{t}}}{\text{h}}_1{\text{h}}_1^{†}{\text{K}}_1^{-1}}{1+\frac{P}{N_{\text{t}}}{\text{h}}_1^{†}{\text{K}}_1^{-1}{\text{h}}_1}\right){\text{h}}_1\\ & =\frac{P}{N_{\text{t}}}{\text{K}}_1^{-1}\left({\text{I}}_{N_{\text{r}}}-\frac{\frac{P}{N_{\text{t}}}{\text{h}}_1{\text{h}}_1^{†}{\text{K}}_1^{-1}}{1+\frac{P}{N_{\text{t}}}{\text{h}}_1^{†}{\text{K}}_1^{-1}{\text{h}}_1}\right){\text{h}}_1\\ & =\frac{P}{N_{\text{t}}}{\text{K}}_1^{-1}\left({\text{h}}_1-\frac{\frac{P}{N_{\text{t}}}{\text{h}}_1{\text{h}}_1^{†}{\text{K}}_1^{-1}{\text{h}}_1}{1+\frac{P}{N_{\text{t}}}{\text{h}}_1^{†}{\text{K}}_1^{-1}{\text{h}}_1}\right)\\ & =\frac{P}{N_{\text{t}}}{\text{K}}_1^{-1}\frac{{\text{h}}_1+\frac{P}{N_{\text{t}}}{\text{h}}_1^{†}{\text{K}}_1^{-1}{\text{h}}_1{\text{h}}_1-\frac{P}{N_{\text{t}}}{\text{h}}_1\left({\text{h}}_1^{†}{\text{K}}_1^{-1}{\text{h}}_1\right)}{1+\frac{P}{N_{\text{t}}}{\text{h}}_1^{†}{\text{K}}_1^{-1}{\text{h}}_1}=\frac{P}{N_{\text{t}}}\frac{{\text{K}}_1^{-1}{\text{h}}_1}{1+\frac{P}{N_{\text{t}}}{\text{h}}_1^{†}{\text{K}}_1^{-1}{\text{h}}_1}.\end{array}$$事实上，$\frac{P}{N_{\text{t}}}\frac{1}{1+\frac{P}{N_{\text{t}}}{\text{h}}_1^{†}{\text{K}}_1^{-1}{\text{h}}_1}$可以视为一个常数，由此可以看到最优的检测器也遵循$c{\text{K}}_1^{-1}{\text{h}}_1$的形式。由于这样的检测器可以使得均方误差达到最小，也被称为最小均方误差检测（minimum mean-square error，MMSE）。由此，得到了滤波器${\text{c}}_1^{\star }$的三条性质：最大输出信噪比、信息无损、最小均方误差。
在解码了第1条数据流的信息后（即得到了$s_1$后），可以把这个数据流从收到的信号向量${\text{y}}_1$中消去，即执行操作${\text{y}}_1-{\text{h}}_1{s}_1$，得到：$${\text{y}}_2={\text{y}}_1-{\text{h}}_1{s}_1={\text{h}}_2{s}_2+\sum _{i=3}^{N_{\text{t}}}{\text{h}}_i{s}_i+\text{n}.$$这个操作被称为干扰消除（interference cancellation）。接下来，需要设计滤波器${\text{c}}_2\in {\mathbb{C}}^{N_{\text{r}}\times 1}$，从${\text{y}}_2$中恢复数据流$s_2$中的信息。仿照之前的思路，可以知道此时最优的滤波器向量为${\text{c}}_2^{\star }=c{\text{K}}_2^{-1}{\text{h}}_2$，其中${\text{K}}_2={\sigma }^2{\text{I}}_{N_{\text{r}}}+\frac{P}{N_{\text{t}}}{\sum }_{i=3}^{N_{\text{t}}}{\text{h}}_i{\text{h}}_i^{†}$表示干扰${\text{z}}_1={\sum }_{i=3}^{N_{\text{t}}}{\text{h}}_i{s}_i+\text{n}$的协方差矩阵，对应的接收端信噪比为${\gamma }_2=\frac{P}{N_{\text{t}}}{\text{h}}_2^{†}{\text{K}}_2^{-1}{\text{h}}_2$，信道容量为${\mathcal{R}}_2=\log \left(1+\frac{P}{N_{\text{t}}}{\text{h}}_2^{†}{\text{K}}_2^{-1}{\text{h}}_2\right)$。注意到，此时的滤波器${\text{c}}_2^{\star }$同样具有最大输出信噪比、信息无损、最小均方误差等三条性质。在解码了第2条数据流的信息后（即得到了$s_2$后），可以把这个数据流从收到的信号向量${\text{y}}_2$中消去，即执行操作$\text{y}-{\text{h}}_1{s}_1$得到：$${\text{y}}_3={\text{y}}_2-{\text{h}}_2{s}_2={\text{h}}_3{s}_3+\sum _{i=4}^{N_{\text{t}}}{\text{h}}_i{s}_i+\text{n}.$$接下来，需要设计滤波器${\text{c}}_3\in {\mathbb{C}}^{N_{\text{r}}\times 1}$，从${\text{y}}_3$中恢复数据流$s_3$中的信息。此时最优的滤波器向量为${\text{c}}_3^{\star }=c{\text{K}}_3^{-1}{\text{h}}_3$，其中${\text{K}}_3={\sigma }^2{\text{I}}_{N_{\text{r}}}+\frac{P}{N_{\text{t}}}{\sum }_{i=4}^{N_{\text{t}}}{\text{h}}_i{\text{h}}_i^{†}$表示干扰${\text{z}}_3={\sum }_{i=4}^{N_{\text{t}}}{\text{h}}_i{s}_i+\text{n}$的协方差矩阵，对应的接收端信噪比为${\gamma }_3=\frac{P}{N_{\text{t}}}{\text{h}}_3^{†}{\text{K}}_3^{-1}{\text{h}}_3$，信道容量为${\mathcal{R}}_3=\log \left(1+\frac{P}{N_{\text{t}}}{\text{h}}_3^{†}{\text{K}}_3^{-1}{\text{h}}_3\right)$。重复上述过程，直至将每一个数据流的信息进行译码。由于上述过程每次都采用能实现最小均方误差的滤波器，同时需要进行一次又一次的干扰消除，这整个译码过程被称为MMSE-SIC译码，其中SIC表示“successive interference cancellation”，即串行干扰抵消。接下来，探究串行干扰抵消是否会减少系统的输入输出互信息，即探究下列关系是否成立：$$\mathcal{R}=\sum _{i=1}^{N_{\text{t}}}{\mathcal{R}}_i.$$为解决上述问题，引入下述引理。
引理2：给定向量$\text{y}$，矩阵$\text{A}\succ \text{0}$、$\text{X}$，有以下关系成立：$$\begin{array}{rl}& \log \det \left(\text{I}+\text{X}{\left(\text{y}{\text{y}}^{†}+\text{A}\right)}^{-1}\right)+\log \det \left(\text{I}+\text{y}{\text{y}}^{†}{\text{A}}^{-1}\right)\\ & =\log \det \left(\text{I}+\left(\text{X}+\text{y}{\text{y}}^{†}\right){\text{A}}^{-1}\right)\end{array}.$$证明：由于${\left(\text{y}{\text{y}}^{†}+\text{A}\right)}^{-1}={\text{A}}^{-1}-\frac{{\text{A}}^{-1}\text{y}{\text{y}}^{†}{\text{A}}^{-1}}{1+{\text{y}}^{†}{\text{A}}^{-1}\text{y}}$，将其代入$\text{I}+\text{X}{\left(\text{y}{\text{y}}^{†}+\text{A}\right)}^{-1}$中可以得到$\text{I}+\text{X}{\left(\text{y}{\text{y}}^{†}+\text{A}\right)}^{-1}=\text{I}+\text{X}{\text{A}}^{-1}\left(\text{I}-\frac{\text{y}{\text{y}}^{†}{\text{A}}^{-1}}{1+{\text{y}}^{†}{\text{A}}^{-1}\text{y}}\right)$。此外，有下述关系成立：$$\begin{array}{rl}& \left(\text{I}+\text{X}{\left(\text{y}{\text{y}}^{†}+\text{A}\right)}^{-1}\right)\left(\text{I}+\text{y}{\text{y}}^{†}{\text{A}}^{-1}\right)\\ & =\left(\text{I}+\text{X}{\text{A}}^{-1}\left(\text{I}-\frac{\text{y}{\text{y}}^{†}{\text{A}}^{-1}}{1+{\text{y}}^{†}{\text{A}}^{-1}\text{y}}\right)\right)\left(\text{I}+\text{y}{\text{y}}^{†}{\text{A}}^{-1}\right)\\ & =\text{I}+\text{y}{\text{y}}^{†}{\text{A}}^{-1}+\text{X}{\text{A}}^{-1}\left(\text{I}-\frac{\text{y}{\text{y}}^{†}{\text{A}}^{-1}}{1+{\text{y}}^{†}{\text{A}}^{-1}\text{y}}\right)\left(\text{I}+\text{y}{\text{y}}^{†}{\text{A}}^{-1}\right)\\ & =\text{I}+\text{y}{\text{y}}^{†}{\text{A}}^{-1}+\text{X}{\text{A}}^{-1}\left(\text{I}-\frac{\text{y}{\text{y}}^{†}{\text{A}}^{-1}}{1+{\text{y}}^{†}{\text{A}}^{-1}\text{y}}+\text{y}{\text{y}}^{†}{\text{A}}^{-1}-\frac{\text{y}{\text{y}}^{†}{\text{A}}^{-1}\text{y}{\text{y}}^{†}{\text{A}}^{-1}}{1+{\text{y}}^{†}{\text{A}}^{-1}\text{y}}\right).\end{array}$$注意到，$$\begin{array}{rl}& \frac{\text{y}{\text{y}}^{†}{\text{A}}^{-1}}{1+{\text{y}}^{†}{\text{A}}^{-1}\text{y}}+\text{y}{\text{y}}^{†}{\text{A}}^{-1}-\frac{\text{y}{\text{y}}^{†}{\text{A}}^{-1}\text{y}{\text{y}}^{†}{\text{A}}^{-1}}{1+{\text{y}}^{†}{\text{A}}^{-1}\text{y}}\\ & =\frac{\text{y}{\text{y}}^{†}{\text{A}}^{-1}+\text{y}{\text{y}}^{†}{\text{A}}^{-1}+{\text{y}}^{†}{\text{A}}^{-1}\text{y}\text{y}{\text{y}}^{†}{\text{A}}^{-1}-\text{y}\left({\text{y}}^{†}{\text{A}}^{-1}\text{y}\right){\text{y}}^{†}{\text{A}}^{-1}}{1+{\text{y}}^{†}{\text{A}}^{-1}\text{y}}=\text{0}.\end{array}$$代入上式，得到$$\left(\text{I}+\text{X}{\left(\text{y}{\text{y}}^{†}+\text{A}\right)}^{-1}\right)\left(\text{I}+\text{y}{\text{y}}^{†}{\text{A}}^{-1}\right)=\text{I}+\text{y}{\text{y}}^{†}{\text{A}}^{-1}+\text{X}{\text{A}}^{-1}.$$根据矩阵的性质$\det \left(\text{A}\text{B}\right)=\det \left(\text{A}\right)\det \left(\text{B}\right)$，可以得到：$$\begin{array}{rl}& \log \det \left(\text{I}+\text{X}{\left(\text{y}{\text{y}}^{†}+\text{A}\right)}^{-1}\right)+\log \det \left(\text{I}+\text{y}{\text{y}}^{†}{\text{A}}^{-1}\right)\\ & =\log \det \left(\text{I}+\left(\text{X}+\text{y}{\text{y}}^{†}\right){\text{A}}^{-1}\right).\end{array}$$由此，引理2得到了证明。

利用上述引理，可以得到下列定理。
定理2：MMSE-SIC译码器是信息无损的，即$\mathcal{R}={\sum }_{i=1}^{N_{\text{t}}}{\mathcal{R}}_i$。[3]
证明：注意到${\mathcal{R}}_i=\log \det \left(\text{I}+\frac{P}{N_{\text{t}}}{\text{h}}_i{\text{h}}_i^{†}{\text{K}}_i^{-1}\right)$，其中${\text{K}}_i={\sigma }^2{\text{I}}_{N_{\text{r}}}+\frac{P}{N_{\text{t}}}\sum _{j=i+1}^{N_{\text{t}}}{\text{h}}_j{\text{h}}_j^{†}$。利用引理2，可以得到，$$\begin{array}{r}{\mathcal{R}}_1+{\mathcal{R}}_2=\log \det \left(\text{I}+\left(\frac{P}{N_{\text{t}}}{\text{h}}_1{\text{h}}_1+\frac{P}{N_{\text{t}}}{\text{h}}_2{\text{h}}_2^{†}\right){\text{K}}_2^{-1}\right)={\bar{\mathcal{R}}}_2,\end{array}$$$$\begin{array}{rl}& {\bar{\mathcal{R}}}_2+{\mathcal{R}}_3=\log \det \left(\text{I}+\left(\frac{P}{N_{\text{t}}}{\text{h}}_1{\text{h}}_1+\frac{P}{N_{\text{t}}}{\text{h}}_2{\text{h}}_2^{†}+\frac{P}{N_{\text{t}}}{\text{h}}_3{\text{h}}_3^{†}\right){\text{K}}_3^{-1}\right)={\bar{\mathcal{R}}}_3.\end{array}$$以此类推，利用归纳法，可以得到：$$\begin{array}{rl}& {\bar{\mathcal{R}}}_{N_{\text{t}}-1}+{\mathcal{R}}_{N_{\text{t}}}\\ & =\log \det \left(\text{I}+\frac{P}{N_{\text{t}}}\left({\text{h}}_{N_{\text{t}}}{\text{h}}_{N_{\text{t}}}^{†}+{\text{h}}_{N_{\text{t}}-1}{\text{h}}_{N_{\text{t}}-1}^{†}+\cdots +{\text{h}}_1{\text{h}}_1^{†}\right){\text{K}}_{N_{\text{t}}}^{-1}\right)={\bar{\mathcal{R}}}_{N_{\text{t}}}.\end{array}$$按照${\text{K}}_i$的定义，${\text{K}}_{N_{\text{t}}}={\sigma }^2{\text{I}}_{N_{\text{r}}}$，代入可得：${\bar{\mathcal{R}}}_{N_{\text{t}}}=\log \det \left(\text{I}+\frac{P}{N_{\text{t}}{\sigma }^2}{\sum }_{i=1}^{N_{\text{t}}}{\text{h}}_i{\text{h}}_i^{†}\right)=\log \det \left(\text{I}+\frac{P}{N_{\text{t}}{\sigma }^2}\text{H}{\text{H}}^{†}\right)=\mathcal{R}.$由此得到结论，$\mathcal{R}={\sum }_{i=1}^{N_{\text{t}}}{\mathcal{R}}_i$，即MMSE-SIC译码器是信息无损的。

接下来，利用图2来描绘整个MMSE-SIC译码过程。
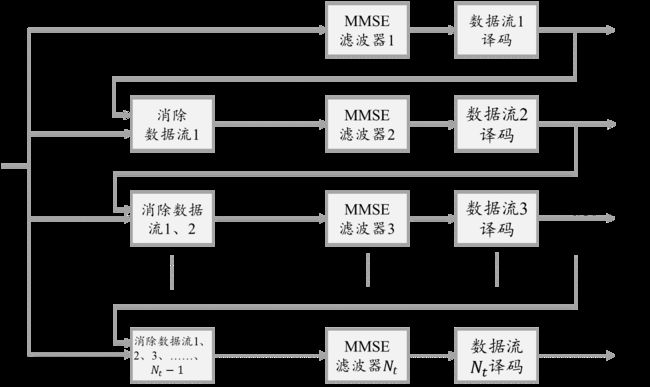图2：MMSE-SIC译码过程。

由此可见，MMSE-SIC译码器可以在保证信息无损的前提下将各个数据流的联合译码化简为各个数据流的串行译码，译码复杂度由指数级降低到了线性级。接下来，考虑更加广义的MIMO传输系统：$$\text{y}=\text{H}\text{B}\mathbf{\Lambda }\text{x}+\text{n},$$其中发送信号$\text{s}=\text{B}\mathbf{\Lambda }\text{x}$的协方差为$\mathbb{E}\left\{\text{s}{\text{s}}^{†}\right\}=\text{B}\mathbf{\Lambda }{\mathbf{\Lambda }}^{†}{\text{B}}^{†}$，$\text{B}$为预编码矩阵， $\mathbf{\Lambda }$为功率分配矩阵（注意根据前面对定理2的证明，在任意功率分配策略下，MMSE-SIC译码都是可以应用的，且信息量没有损失）。此时，接收端只需要将$\text{H}\text{B}\mathbf{\Lambda }$视为有效信道矩阵再采用MMSE-SIC译码器串行地译出 中各个数据流的信息。

以下，给出具体的Matlab代码来说明MMSE-SIC译码器的性能。

Power = [-10:5:30]; % 发送功率 (dB)
noise = 1; % 噪声功率 (0dB)
Nt = 6; % 发端天线数
Nr = 8; % 收段天线数
Monte_Carlo = 50; % 蒙特卡洛仿真次数
Capacity = ones(1,length(Power)); % 存储信道容量
Tmp = ones(Monte_Carlo,length(Power));
Tmp1 = ones(Monte_Carlo,length(Power));
for Monte = [1:1:Monte_Carlo]
    for power_index = [1:1:length(Power)]
        [Monte,power_index]
        P = 10^(Power(power_index)/10);
        H = 1/sqrt(2)*randn(Nr,Nt) + 1j*1/sqrt(2)*randn(Nr,Nt); % MIMO信道(考虑瑞利衰落模型)
        %% 使用联合译码时的信道容量
        Capacity1 = abs(log(det(eye(Nr)+P/Nt*(H*H'))));
        %% 存储结果
        Tmp(Monte,power_index) = Capacity1;
        %% 使用MMSE-SIC译码器的信道容量
        Capacity2 = 0;
        for stream = [1:1:Nt]
            K = eye(Nr)+P/Nt*(H(:,[(stream+1):1:Nt])*H(:,[(stream+1):1:Nt])');
            Capacity2 = Capacity2 + abs(log(det(eye(Nr)+P/Nt*H(:,stream)*H(:,stream)'*inv(K))));
        end
        %% 存储结果
        Tmp1(Monte,power_index) = Capacity2;
    end
end
plot(Power,mean(Tmp),'-o');
hold on;
plot(Power,mean(Tmp1),'-x');
xlabel('发送功率 [dB]');
ylabel('传输速率 [bps/Hz]');
legend('联合译码','MMSE-SIC译码');
grid on;

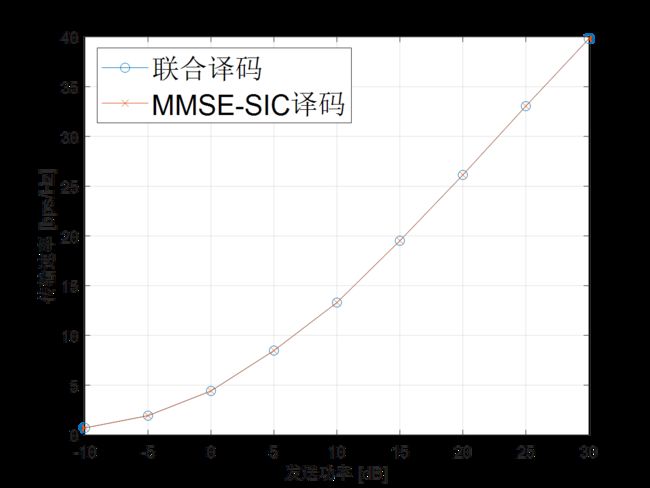图3：MIMO传输速率与发送功率的关系，信道采用瑞利衰落模型，蒙特卡洛仿真次数设置为50，$N_{\text{t}}=6$ ，$N_{\text{r}}=8$ ，${\sigma }^2=1$ 。

图3绘制了传输速率随传输功率变化的曲线，从图中可以看出，联合译码与MMSE-SIC译码可以实现相同的传输速率。

最后，对上述内容进行总结。对于MIMO信道而言，当发射机不知道信道信息时，发射机与接收机需使用如下的结构：

1. 发射机采用平均功率分配，为每个数据流分配相同的功率；
2. 接收机采用MMSE-SIC译码器对接收到的信号进行译码。MMSE-SIC译码器具有三大性质：使输出信噪比最大、无信息损失、使均方误差最小。

参考文献

1. I. E. Telatar, “Capacity of multi-antenna Gaussian channels,” Eur. Trans. Telecom, vol. 10, pp. 585–595, Nov. 1999.
2. S. Boyd and L. Vandenberghe, Convex Optimization. Cambridge, U.K.: Cambridge Univ. Press, 2004.
3. D. Tes and P. Viswanath, Fundamentals of Wireless Communication. Cambridge, U.K.: Cambridge Univ. Press, 2005.