2022 ICPC 杭州站（补题记录）

题目顺序大致按照难度排列。

 

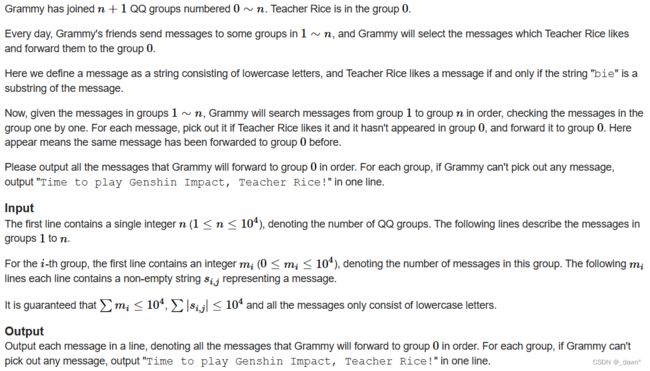
F. Da Mi Lao Shi Ai Kan De（模拟）

有0~m个群，老师在0群中，G在1~n群中，对于每个群，G需要将老师感兴趣的信息转到0群，老师感兴趣的信息指对应字符串中存在“bie”子串，按照顺序转发，且转发内容不能有重复的，输出需要转到0群的信息，若是某个群没有需要转的信息，输出那一串东西。

思路：模拟即可。

AC Code：

#include 

typedef long long ll;
typedef std::pair PII;
const int N = 2e5 + 5;
int t, n;

int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(0);
	std::cout.tie(0);
	std::cin >> t;
	std::map mp;
	while(t --) {
		std::cin >> n;
		bool flag = false;
		for(int i = 1; i <= n; i ++) {
			std::string s;
			std::cin >> s;
			for(int j = 0; j < (int)s.length() - 2; j ++) {
				if(s[j] == 'b' && s[j + 1] == 'i' && s[j + 2] == 'e' && !mp[s]) {
					flag = true;
					mp[s] ++;
					std::cout << s << '\n';
					break;
				}
			}
		}
		if(!flag)
			std::cout << "Time to play Genshin Impact, Teacher Rice!" << '\n';
	}
	return 0;
}

 D. Money Game（打表找规律）

给出一个数列，从第一个开始，第一个给第二个数自己的一半，第二个数给第三个数自己的一半，到最后的一个数，将自己的一半给第一个数。循环那一坨次数，问最后数组变成了什么样。

思路：一般看到这种循环一大堆的题，先考虑打表找规律。很显然，这个题打表后，发现自己造的样例都会变成这样：数组和为sum，第一个数是sum / (n + 1) * 2，其他的数都是sum / (n + 1)，这样输出就可以了，注意保留小数。

AC Code：

#include 

typedef long long ll;
const int N = 1e6 + 5;
int n;
double a[N];

int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(0);
	std::cout.tie(0);
	std::cin >> n;
	double sum = 0;
	for(int i = 1; i <= n; i ++) {
		std::cin >> a[i];
		sum += a[i];
	}
	double res = sum / (n + 1);
	std::cout << std::fixed << std::setprecision(10);
	for(int i = 1; i <= n; i ++) {
		if(i == 1)
			std::cout << res * 2;
		else
			std::cout << ' ' << res;
	}
	std::cout << '\n';
	return 0;
}

A. Modulo Ruins the Legend（exgcd，等差数列性质运用）

 给出一个数组a，构造一个等长度的等差数列b，使得对m取模后最小，输出这个取模后的最小值和等差数列的首项s和公差d。

思路：（1）看到网上的题解大多是这样的思路，比较容易想到：

我们要求的是：

sum + s * n + n * (n + 1) / 2 * d，（1）

假设结果是ans，因为s和d都是未知数，对于二元一次不定方程而言，根据扩展欧里几德性质知道：

s * n + n * (n + 1) / 2 * d = k2 * gcd(n, n * (n + 1) / 2)，(2)

其中k2是任意的整数，所以我们要求的原式可以写为：

sum + k2 * g = ans - k1 * m（g = gcd(n, n * (n + 1) / 2)，减去的k1 *m是取模改为这样的写法）；

移项可得：

k2 * g + k1 * m = ans - sum （3）

因为ans的取值范围是[0, m - 1]，所以上式两侧的取值范围都是：[-sum, m - 1 - sum]，

上式中可设x = gcd(g, m)，设系数为z，则有z * x >= -sum，可以得到z的最小值-sum / x，至此，因为g是已知的，m已知，所以x已知；sum已知，所以z已知，又因为（3）式可以写为：

z * x = k1 * m + k2 * g，由exgcd可以求得k1，k2，k1知道了，（2）式由exgcd可以求得结果。

（2）看到官方题解，一开始看着比较抽象，去问了师哥，大致是这样的：

官方题解运用了等差数列的性质，对于等差数列而言，第i项和第n - i项的和是中间项的两倍，分奇偶讨论：当n为奇数时，这个条件显然存在，所以无论等差数列长什么样子，我们都可以把它写成d为0的一个数列，即常数列，所以d完全可以取0，对于和并不影响；n为偶数时，它的中间项不一定是整数，但是对于任意的偶数项且中间项不是整数的等差数列，我们都可以写成公差为1的数列，例如0,3,6,9可以写成3,4,5,6，这样公差为1；当然，当中间项是整数时，同奇数。通过这种方式，我们可以确定d的取值0或1，这是完全符合题目要求的特殊值。消去了一个未知数，还剩下一个，原式可写为：

sum + n * s = ans - k * m；

换一下位置：

n * s + k * m = ans - sum；

这样可以用exgcd求解，也可以枚举k的取值，k是一定小于n的。

为什么小于n？若k > n，则可以写成k = k1 + n，原式为n * s + (k1 + n) * m，这个带有n的项展开后可以合并到前面。

AC Code：

仅提供方法一的代码，注意开__int128。方法二可以自己试试嗷~

#include 

typedef long long ll;
const int N = 1e6 + 5;
ll n, m;

ll gcd(ll a, ll b) {
	return b ? gcd(b, a % b) : a;
}

ll exgcd(ll a, ll b, __int128 &x, __int128 &y) {
	if(!a) {
		x = 0, y = 1;
		return b;
	}
	ll d = exgcd(b % a, a, y, x);
	x -= b / a * y;
	return d;
}

int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(0);
	std::cout.tie(0);
	std::cin >> n >> m;
	ll sum = 0;
	for(int i = 1; i <= n; i ++) {
		ll x;
		std::cin >> x;
		sum += x;
	}
	ll g = gcd(n, n * (n + 1) / 2);
	ll gg = gcd(g, m);
	ll l = -sum / gg;
	ll ans_sum = l * gg;
	ll ans = ans_sum + sum;
	__int128 k1, k2, s, d;
	exgcd(m, g, k1, k2);
	k1 *= l, k2 *= l;
	exgcd(n, n * (n + 1) / 2, s, d);
	s *= (ans_sum - k1 * m) / g;
	d *= (ans_sum - k1 * m) / g;
	s = (s % m + m) % m, d = (d % m + m) % m;
	std::cout << ans << '\n';
	std::cout << (ll)s << ' ' << (ll)d << '\n';
	return 0;
}

C. No Bug No Game（背包变形）

给出n个物品，以及每个物品的体积，还有选择不同重量的部分的价值，向容量为k的背包里装入物品，当背包容量足够时，必须装入一整个物品；不够时，可以装入部分，求可以装的最大价值。

思路：因为背包容量足够时，必须装入一整个，所以部分装入的必定只有一个物品。粗略的想，我们可以枚举最后被装入的这一部分物品及体积，设这个部分体积是k，然后若前一部分用了j体积的话，后半部分就是m - k - j，这样就是一个完整的背包问题了。但是我们不能枚举物品和体积再对前后两部分进行背包dp，这样必定超时，可以采用前后缀背包优化，设三位数组f[i][j][k]第一维0代表前缀，1代表后缀，后面两位同01背包dp的两维，通过预处理降低时间复杂度。

AC Code：

#include 

typedef long long ll;
const int N = 3e3 + 5;
int n, k, x;
int p[N], w[N][15], f[2][N][N];

int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(0);
	std::cout.tie(0);
	std::cin >> n >> k;
	int sum = 0;
	for(int i = 1; i <= n; i ++) {
		std::cin >> p[i];
		sum += p[i];
		for(int j = 1; j <= p[i]; j ++) {
			std::cin >> w[i][j];
		}
	}
	if(sum < k) {
		int ans = 0;
		for(int i = 1; i <= n; i ++) {
			ans += w[i][p[i]];
		}
		std::cout << ans << '\n';
		return 0;
	}
	memset(f, -1, sizeof(f));
	f[0][0][0] = 0;
	f[1][n + 1][0] = 0;
	for(int i = 1; i <= n; i ++) {
		for(int j = 0; j <= k; j ++) {
			f[0][i][j] = f[0][i - 1][j];
			if(j >= p[i] && f[0][i - 1][j - p[i]] != -1)
				f[0][i][j] = std::max(f[0][i][j], f[0][i - 1][j - p[i]] + w[i][p[i]]);
		}
	}
	for(int i = n; i >= 1; i --) {
		for(int j = 0; j <= k; j ++) {
			f[1][i][j] = f[1][i + 1][j];
			if(j >= p[i] && f[1][i + 1][j - p[i]] != -1)
				f[1][i][j] = std::max(f[1][i][j], f[1][i + 1][j - p[i]] + w[i][p[i]]);
		}
	}
	int ans = 0;
	for(int i = 1; i <= n; i ++) {
		for(int j = 1; j <= p[i]; j ++) {
			int res = k - j;
			for(int l = 0; l <= res; l ++) {
				int r = res - l;
				if(f[0][i - 1][l] != -1 && f[1][i + 1][r] != -1)
					ans = std::max(ans, w[i][j] + f[0][i - 1][l] + f[1][i + 1][r]);
			}
		}
	}
	std::cout << ans << '\n';
	return 0;
}

 K. Master of Both（字典树）

给出n个字符串，m种字母顺序，对于每一种字母顺序，输出给出的字符串有多少逆序对。

思路：因为数据范围较大，所以我们不能对于每一种顺序都跑一边求逆序对，所以需要预处理得到求逆序对的方式。因为对于每两个字符串而言，决定其顺序的是一对字母，即从头数开始不同的那对字母，考虑设cnt[a][b]表示由字母对(a, b)决定的两个字符，且含有a的字符串编号小于b，n个字符串中逆序对的个数，这样在新的顺序下如果a的字典序大于b，则就会有cnt[a][b]的贡献。而我们要求cnt数组，可以在建立字典树的时候，给每一个字母加上现有确定字母对决定关系的数量，这样的顺序就是按照编号大小来的。

参考大佬的思路！

AC Code：

#include 

typedef long long ll;
const int N = 2e6 + 5;
const int mod = 1e9 + 7;
int n, m, idx;
int sum[N][30];
int pos[30], mp[N][30];
char s[N];
ll cnt[30][30];

void insert() {
	int p = 0;
	for(int i = 0; s[i]; i ++) {
		int u = s[i] - 'a' + 1;
		if(!mp[p][u]) mp[p][u] = ++ idx;
		for(int j = 0; j < 27; j ++) {
			cnt[j + 1][u + 1] += sum[p][j];
		}
		sum[p][u] ++;
		p = mp[p][u];
	}
}

int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(0);
	std::cout.tie(0);
	std::cin >> n >> m;
	for(int i = 1; i <= n; i ++) {
		std::cin >> s;
		int len = strlen(s);
		s[len] = 'a' - 1;
		s[len + 1] = 0;
		insert();
	}
	while(m --) {
		std::cin >> s + 1;
		s[0] = 'a' - 1;
		for(int i = 0; i < 27; i ++) {
			pos[s[i] - 'a' + 1] = i;
		}
		ll ans = 0;
		for(int i = 0; i < 27; i ++) {
			for(int j = 0; j < 27; j ++) {
				if(pos[i] > pos[j])
					ans += cnt[i + 1][j + 1];
			}
		}
		std::cout << ans << '\n';
	}
	return 0;
}

杭州站是我们队第一场区域赛，因为疫情打的七零八落，一直也没补题，补一下题~