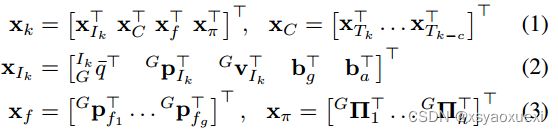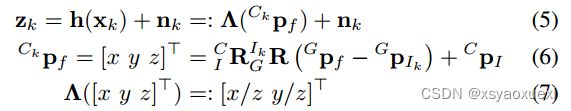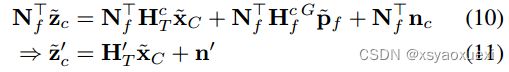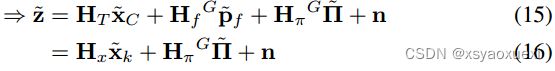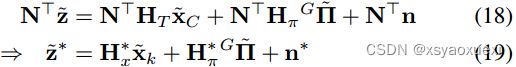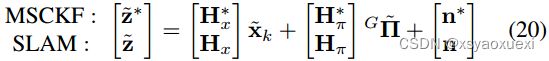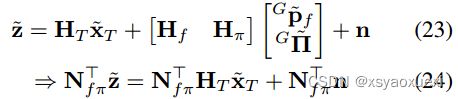vslam论文14：Monocular Visual-Inertial Odometry with Planar Regularities（ICRA 2023）

摘要

       最先进的单目视觉惯性里程计(VIO)方法依赖于稀疏点特征，部分原因是它们的效率、鲁棒性和普遍性，而忽略了高级结构规律，如平面，这些在人造环境中很常见，可以用来进一步约束运动。一般来说，由于平面的存在空间很大，可以用相机观察平面很长一段时间，因此可以进行长期导航。所以，在本文中，我们设计了一种新颖的实时单目VIO系统，该系统在轻量级多状态约束卡尔曼滤波器(MSCKF)中由平面特征完全正则化。我们的方法的核心是一种高效鲁棒的基于单眼的平面检测算法，它不需要额外的传感模式，如文献中常见的双目或深度相机，同时能够实时正则化点特征到环境平面。具体来说，在本文提出的MSCKF中，长期存在的平面保持在状态向量中，而较短的平面在使用后被边缘化以提高效率。平面规律应用于状态内SLAM特征和状态外MSCKF特征，充分利用环境平面信息提高VIO性能。通过广泛的蒙特卡罗模拟和不同的现实世界实验(包括作者收集的AR场景)对所提出的方法进行了评估，并证明在结构化环境中优于基于点的VIO。

开源：rpng/ov_plane: A monocular plane-aided visual-inertial odometry (github.com)

演示视频：https://youtu.be/bec7LbYaOS8 

AR桌子数据集：https://github.com/rpng/ar_table_dataset

I. 引言和相关工作

我们的主要贡献包括:

（1）我们设计了一个高效的单目VIO估计器，通过点平面几何约束检测和执行平面规律，它能够估计长寿命的SLAM平面特征或直接边缘化短寿命的平面特征以提高效率。我们还研究了状态内SLAM和状态外MSCKF点特征的平面正则化。

（2）我们开发了一种新颖且鲁棒的平面检测和跟踪算法，该算法利用稀疏VIO点特征规范的两两比较，无需昂贵的密集深度图或神经网络计算即可实现实时估计。

（3）我们在蒙特卡罗模拟和现实世界实验中广泛验证了所提出的系统，并发布了作者收集的数据集，以造福社区。

II. 系统概述

算法1概述了该方法的主要步骤，其关键思想是利用平面结构的(通常)大空间特性来延长特征轨迹，从而进一步提高估计精度。

A.状态向量

       在时刻tk，系统状态xk由当前导航状态xIk，历史IMU位姿克隆xC，以及3D环境(SLAM)点特征xf和(SLAM)平面特征xπ的子集组成:

 B. IMU运动学传播

       利用惯性运动学将状态从时刻tk演化到时刻tk+1 [58]， [59]:

        其中线加速度和角速度ωmk测量值受到零均值高斯白噪声的污染，MSCKF将该非线性模型线性化，并向前传播状态估计和协方差。

C. 非平面点特征更新

       相机提供环境三维点的方位观察。这些观测值可以使用以下测量函数来更新我们的状态(注意，这里我们假设的是全局3D特征模型):

 线性化Eq.(5)得到如下系统:

       其中HTk和Hfk是相对于观测位姿x @ Tk和三维点特征G @ pf的测量雅可比矩阵。然后，我们可以将不同时间步长的测量值“叠加”起来，得到:

        式中z ~ c为叠加测量残差;HcT和Hcf是堆叠的雅可比矩阵;nc ~ N (0, Rc)是叠加的测量噪声(通常为1像素)。然后，我们使用两种不同类型的非平面点特征执行EKF更新:

SLAM点:状态xf包含Gpf，因此Eq.(9)可以直接使用标准EKF方程更新状态。

MSCKF点:对于不处于状态的特征，我们将Eq.(9)投影到Hc f的左零空间上(即具体来说，我们可以构造如下不依赖于的系统:

        这降低了过滤器的计算复杂度，因为不需要将特征插入状态。

III. 平面规律

A. 正则化约束的测量

       所提出的VIO系统通过点对面约束来实现平面规则性。考虑一个位于GΠ平面上的点特征Gpf，我们有:

B.平面恢复和非线性细化

       为了加强点对平面的约束，Eq.(13)，我们首先通过对一组共面点特征执行RANSAC来稳健地恢复平面的初始猜测(关于我们如何提取共面集的详细信息在算法2中)。平面估计可以通过以下线性系统从至少三个点求解:

       得到π后，可以用Gn = π/||π|、Gd = 1/||π|来回收平面。根据点到面距离阈值选择RANSAC内嵌集，见式(12)，恢复效果最好的平面具有最多的内嵌体和最小的平均点到面距离。

       如果找到足够数量的内层，我们使用固定的相机姿势对点特征和面进行联合细化。在优化过程中，平面上的SLAM点是固定的，但为了进一步改善平面估计，需要通过点对平面的约束来包含SLAM点。非线性优化问题使用式(5)和式(12)表示，并使用ceres-solver求解，耗时0.51.5毫秒(ms)。

C. 平面特征初始化

       对于MSCKF平面点特征，与MSCKF特征边缘化类似，我们将Eq.(15)投影到左侧Hf的零空间(即)，得到与点特征无关的平面GΠ残差函数:

对于SLAM点特征，可以直接使用Eq.(16)。在收集共面MSCKF [Eq.(19)]和SLAM [Eq.(16)]点特征测量值后，我们将它们叠加成以下线性系统:

D. 平面合并

       一旦有足够的观测，平面就被初始化到这种状态，并不断地用新的测量来改进它们。随着时间的推移，多个平面可能合并为一个公共平面，以减少状态中的冗余。如果超过一个平面驻留在状中，则执行成对状态约束更新以强制平等，然后将除一个平面外的所有平面边缘化。例如，平面GΠ1和GΠ2有:

E. 平面的点特征更新

       给定平面点特征线性化测量函数Eq.(14)，我们将详细解释如何处理具有状态内或状态外特征的测量。然后我们考虑以下更新方法:

•SLAM平面+ SLAM点:标准EKF更新

•SLAM平面+ MSCKF点:通过零空间投影去除点特征依赖[参见Eq.(18)]。

•MSCKF平面+ SLAM点:删除平面特征依赖:

       其中Nπ是堆叠的Hπ的左零空间。这需要3个以上的平面点特征。

•MSCKF平面+ MSCKF点:删除平面和点的特征依赖:

式中Nfπ为[Hf Hπ]的左零空间，观察一个特征三次以上是必要的。

IV. 蒙特卡罗仿真

       所提出的ov平面是作为OpenVINS的扩展而构建的。我们在模拟轨迹和平面上的视觉点周围生成一个房间，如图2所示。假设点与平面之间的数据关联是已知的。表1包含模拟中使用的关键传感器频率、传感器属性和噪声参数。

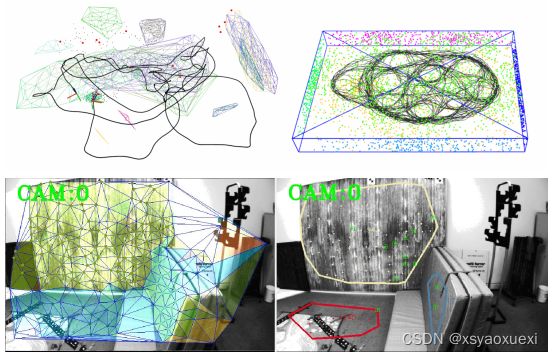
图2：EuRoC MAV，估计平面显示为网格(并非全部在状态向量中，左上角)。模拟环境(上，右)在15.2 × 9.5 × 1.7m的房间中有1.2km的轨迹(点按平面着色)。下一行为V1_01稀疏跟踪网格，左图为法线，右图为提取平面。

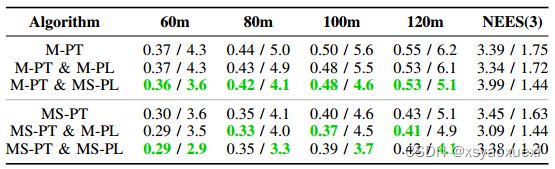
       在不同的实验中，使用归一化估计误差平方(NEES)、相对姿态误差(RPE)和绝对轨迹误差(ATE)指标报告误差(见[64]和[65])。表2显示了使用不同的估计器配置运行20次蒙特卡罗的结果。所有算法都保持一致，因为它们的NEES值接近于3。M-PT和M-PL增加了MSCKF飞机，与基线M-PT系统相比几乎没有改进。我们将此归因于MSCKF平面轨迹长度仅为滑动窗口大小的长度，并且规律性并没有大大改善MSCKF点线性化。但是，如果将具有足够观测值的平面插入到状态向量MPT和MS-PL中，那么对于所有轨迹长度都可以看到明显的性能增益。在模拟中，可以在轨迹的重要部分上跟踪天花板和地板，从而改进特征三角测量并利用结构规则信息。

       接下来，我们研究了SLAM点平面共估计的影响。正如预期的那样，基线MS-PT比M-PT更准确，但有趣的是，MPT和MS-PL能够在最多只能估计六个环境平面与MSCKF点特征的情况下执行接近准确度的水平。同样，MSCKF平面，MS-PT和M-PL对仅点MS-PT的精度影响较小，而在MS-PT和MS-PL中添加SLAM平面估计具有整体最佳精度。仿真结果表明，对于状态内SLAM和状态外MSCKF点特征，VIO性能都具有平面规律。

V. 现实世界实验

       我们在EuRoC MAV数据集的Vicon房间场景中评估了所提出的系统。

A. 平面检测和追踪

       在算法2中总结了平面提取的细节，在图2的底部可以看到一个恢复法线的提取示例。

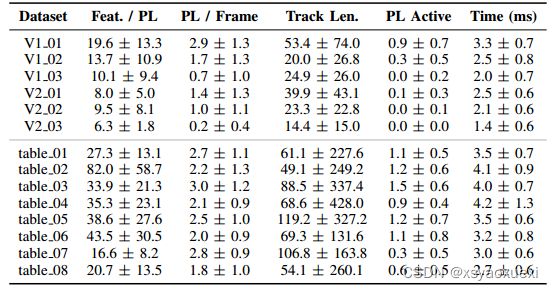
       我们在一系列数据集上运行了所提出的平面跟踪器，并将其统计结果总结在表5中。平面检测和匹配的额外计算成本约为2-4ms，与稀疏点特征跟踪相似(约为3-4ms)。

       在自收集的AR表数据集上，我们观察到，由于更大的平面和更长的观察时间，平面可以被充分跟踪很长一段时间，每个平面有大量的特征。为了利用结构规律，这是可以修改的。此外，由于没有提取视觉点特征以方便平面检测，因此不可能利用环境白墙。因此，平面的提取仍然局限于具有足够纹理的区域。

表5:跟踪统计和执行平面跟踪的时间(即不包括稀疏点跟踪)。

统计数据包括:每平面特征、每帧平均平面、每帧平均平面跟踪长度、每帧处于活动状态的平面。

B. EuRoC MAV室内数据集

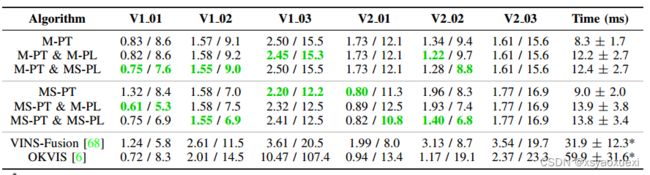
表III显示了不同配置下每个数据集的平均ATE。

表三:EuRoC MAV ATE(度/厘米)以及V1 01 easy数据集的平均时间。采用σd = 0.01。

C. AR表数据集 

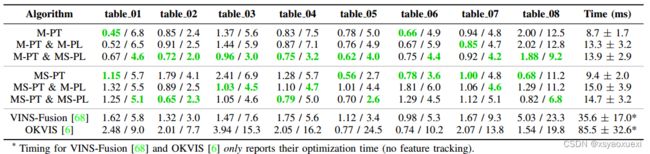
表4:表01数据集的自收集AR表ATE(度/厘米)和平均时间。采用σd = 0.01。

 从M-PT中可以明显看出，当使用平面规律时，精度显著提高了1-3cm。