基础练习之链表

简单介绍

链表，每个节点离散的分布在内存中，通过next指针将节点进行连接(双向链表多一个指针pre)。由于存在额外的指针，内存空间会比正常存储数据要多一些。

一般结构

单链表节点

struct Node{
    TYPE val;
    struct Node* next;
};

双向链表节点

struct Node{
    TYPE val;
    struct Node* pre;
    struct Node* next;
};

一般操作

链表的建立

此处讨论的是不包含头指针的链表

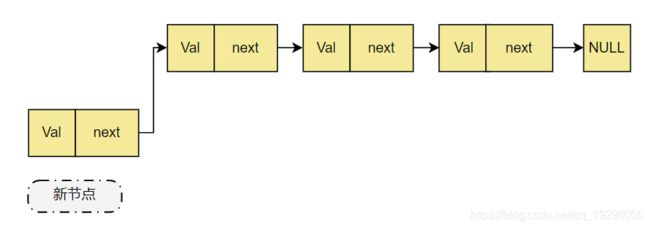
头插法

每次新添加的节点都变为头节点。

每次添加一个节点

typedef TYPE int;
Node * insert(Node*head,TYPE val){
    Node * p = new Node();
    p->val = val;
    p->next = head;
    return p;
}

一次添加所有

Node * create_head(){
    // 头插法
    Node * p=NULL;
    Node * head = NULL;
    int val;
    cin >> val;
    while(val !=-1){
        p = new Node();
        p->val = val;
        p->next = head;
        head = p;
        cin >> val;
    }
    return head;
}

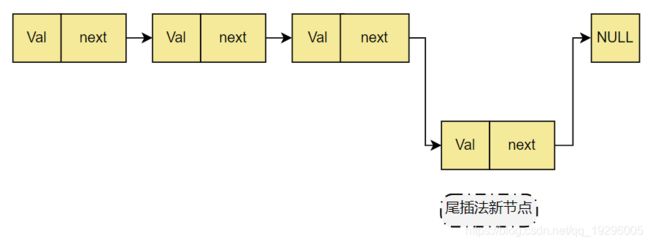
尾插法

每次进来的节点为链表的尾插入到最后。

每次添加一个节点

Node * insert_tail(Node*head,TYPE val){
    //尾插法，如果head == NULL 返回 节点 否则返回 NULL
    Node * p = new Node();
    p->val = val;
    p->next = NULL;
    if(head == NULL){
        return p;
    }
    while(head->next!=NULL){
        head = head->next;
    }
    head->next = p;
    return NULL;
}

一次添加所有

Node * create_tail(){
    // 尾插法
    Node * tail=NULL;
    Node * p = NULL;
    Node * head = NULL;
    int val;
    cin >> val;
    while(val !=-1){
        p = new Node();
        p->val = val;
        if(head == NULL){
            head = p;
        }else{
            tail->next = p;
        }
        tail = p;
        cin >> val;
    }
    tail->next = NULL;
    return head;
}

插入数据

插入到第n个节点之后,分3中情况

1 头节点为空，直接返回新的节点
2都节点不为空，但是没有n个节点，直接插入到最后
3正常插入到第n个节点后面。

Node * insert_n(Node * head,TYPE val,int n){
    //插入到第n个元素之后，如果没有n个，直接插入到最后
    //head 为NULL 返回新head，否则返回NULL
    Node *p = new Node();
    p->val = val;
    if(head == NULL){
        p->next = NULL;
        return p;
    }
    int count = 1;
    while(countnext){
        head = head->next;
        ++count;
    }
    if(n == count){
        p->next = head->next;
        head->next = p;
    }else{
        head->next = p;
        p->next = NULL;
    }
    return NULL;
}

删除数据

删除第n个节点的数据

1 头节点为空，直接返回空
2 删除的数据为头节点，链表只有一个节点，返回空
3 删除的数据为头节点，链表不只一个节点，返回之后的节点
4 正常删除第n个节点的数据（或没有第n个节点），返回头节点

Node * delete_n(Node *head,int n){
    // 1 头节点为空，直接返回空
    // 2 删除的数据为头节点，链表只有一个节点，返回空
    // 3 删除的数据为头节点，链表不只一个节点，返回之后的节点
    // 4 正常删除第n个节点的数据（或没有第n个节点），返回头节点
    // n 从1开始
    if(head == NULL || n<=0){
        return head;
    }
    int count = 1;
    Node *p = head;
    if(n == 1){
        head = p->next;
        delete p;
        return head;
    }
    while(count next){
        ++count;
        p = p->next;
    }
    if(count == n-1){
        Node * q = p->next;
        if(q!=NULL){
            p->next = q->next;
            delete q;
        }
    }
    return head;
}

查找

查找给定的val是否存在，存在返回true,不存在返回false

bool find(Node* head,TYPE val){
    while(head){
        if(head->val == val){
            return true;
        }else{
            head = head->next;
        }
    }
    return false;
}

一般考点 部分参考来源

链表反转

初始链表，p为空指针，q指向头节点

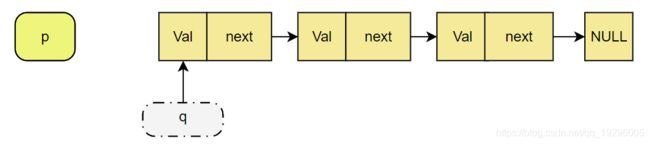
指针t指向q的下一个节点，将q的下一个节点指向p，即将q的红色箭头变为绿色箭头。

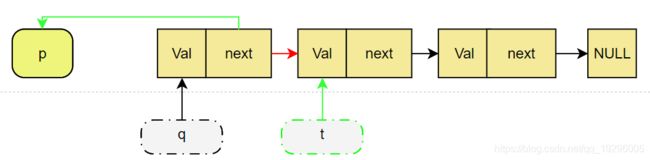
p 变成q,q变成t，即图中红色指针变为绿色指针

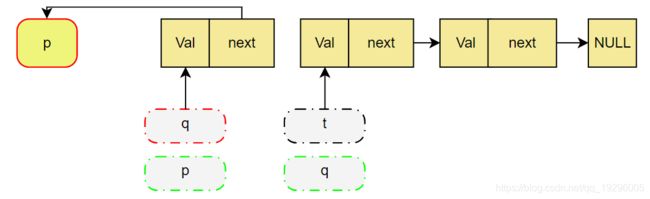
循环执行2和3 直到 q == NULL为止，返回p.

Node * reverse(Node* head){
    Node* p = 0;
    Node* q = head;
    Node* t = NULL;
    while(q!=NULL){
        t = q->next;
        q->next = p;
        p = q;
        q = t;
    }
    return p;
}

两个链表找交叉节点(判断是否相交)

对齐法

如图，如果找到两个链表的头部对齐的起点，然后两个链表一次移动并判断一个，相等时，就为找到的交点，否则就不相交。
对两个链表计数，长的链表有countA个节点,短的链表有countB个节点。先移动短的链表，移动(countA - countB)个位置，然后两个链表一起移动并判断是否相等。相等就是交叉点，移动到结尾都不相等则不相交。

时间复杂度 O(A+B)
空间复杂度 O(1)
不会破环原来的链表结构

环找入口点法

这种方法其实是转化为找带环的链表的入口点，将其中一条链表的首尾相连。具体解发见找"链表环所在位置"

哈希解法

将第一个链表的节点地址存到哈希表中，然后遍历第二个链表，找到第一个存在于哈希表中的节点就是交叉节点。

时间复杂度 O(A+B)
空间复杂度 O(A)

找链表环入口所在位置

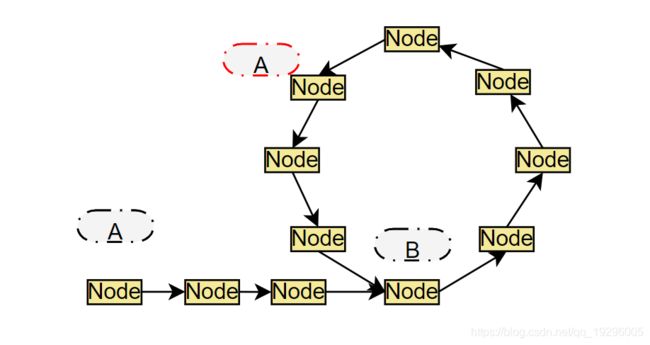
如图所示，假设黑色的A节点绕进到圈内，和红色的A重合了。将红色A作为起点，两个指针，一个走一步，一个走两步。第一次相交的位置会在起点。此时一个指针在红A,一个指针在黑A,同时都走一步，两个节点相等时找到环的入口节点B。

Node * has_ring(Node * head){
    //有环返回环的入口，否则返回NULL,不可以改变原链表
    if(head == NULL || head->next == NULL){
        return head;
    }
    Node* slow = head->next;
    Node* fast = head->next->next;
    while(fast&&fast->next!=NULL && fast!=slow){
        slow = slow->next;
        fast = fast->next;
        if(fast){
            fast = fast->next;
        }
    }
    if(fast == slow){
        fast = head;
        while(slow != fast){
            slow = slow->next;
            fast = fast->next;
        }
        return fast;
    } 
    return NULL;

}

求倒数k个节点

先让p指针从head移动k个节点，此时让a指针指向head，p和a同时移动，p到达链表尾部时，a到达倒数第k个位置。

Node *countdown_k(Node* head,int k){
    //倒数k个节点
    if(k<1){
        return NULL;
    }
    int count = 0;
    Node *p = head;
    while(countnext;
        ++count;
    }
    if(p){
        Node*a = head;
        while(p->next){
            p = p->next;
            a = a->next;
        }
        return a->next;
    }
    return NULL;
}

代码整理

点击这里