代码随想录 Day37 完全背包理论基础 卡码网T52 LeetCode T518 零钱兑换II T377 组合总和IV

完全背包理论基础

0-1背包理论基础:0-1背包理论基础

完全背包就是在0-1背包的基础上加上了一个条件,0-1背包中每个物品只能选择一次,而在完全背包上一个物品可以选择多次,其实也很简单,只需要修改一部分的代码就可以实现,没了解过0-1背包的友友可以去看我的0-1背包理论基础,下面我们开始分析他们的不同点.

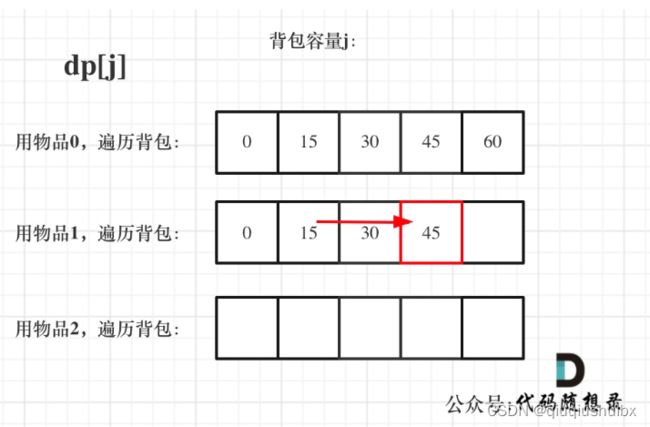
两者的唯一区别就在遍历顺序上(基于一维数组方式讲解)

0-1背包选择先遍历物品,再遍历背包,同时在遍历背包的时候采用倒序遍历,目的就是保证每个物品只被使用一次,其实我们只需要修改成正序遍历即可,这时候,每个物品就可以被多次添加了. 

我们还是举个例子说明

我们的背包容量是4,可以装一下物品,物品数量无限

此时我们尝试先遍历物品后遍历背包和先遍历背包后遍历物品两种方式

1.先物品后背包

我们发现其实dp数组的更新顺序是从左向右的,只与它的前一个状态有关.

2.先背包后物品

这里其实就是列向更新数据,从上向下更新数据,也只与前一个状态有关.

所以这里的遍历顺序是两种都可以.

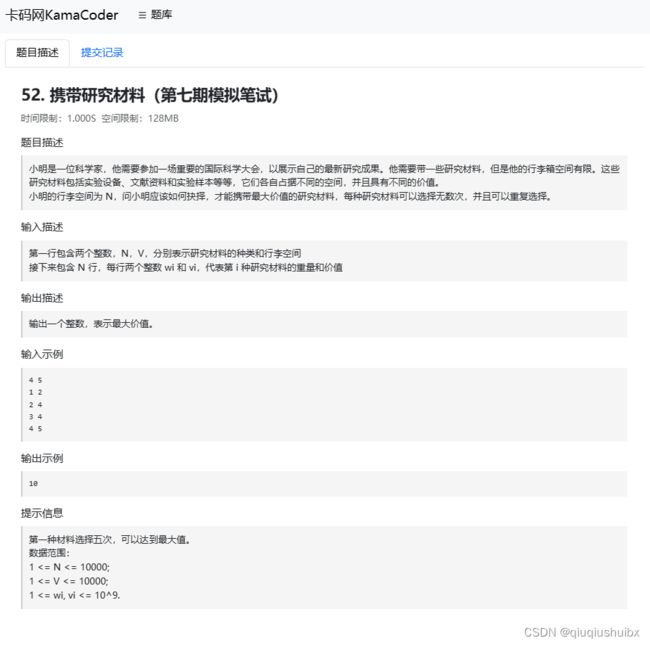
卡码网T52 携带研究材料

题目链接:题目页面 (kamacoder.com)

题目思路:

和之前一样,利用动规五部曲解决问题,这题是一道标准的完全背包问题

不过在卡码网上需要自己手动进行输入输出和导包

1.dp数组含义

这里dp数组的含义是装满行李箱的研究材料的最大价值

2.递推公式

和0-1背包是一样的,这里不做过多赘述

dp[j] = Math.max(dp[j],dp[j-weight[i]]+value[i]);

3.初始化

dp[0] = 0;是一个默认的初始化,所以直接不用写就行.

4.遍历顺序

这里上面说了,先遍历背包和先遍历物品都是可以的,但是要注意遍历背包的时候是从小往大遍历,不需要倒序遍历了.因为倒徐遍历会默认将价值最大的物品只加入一个进入dp[j]的坐标中,具体可以自己模拟试试看或者参考我对0-1背包的理解

5.打印dp数组排错

代码解析:

import java.util.*;

public class Main {
    public static void main (String[] args) {
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();
        int V = sc.nextInt();
        int[] dp = new int[V+1];
        int[] weight = new int[N];
        int[] value = new int[N];
        int i = 0;
        while(sc.hasNext()){
            weight[i] = sc.nextInt();
            value[i] = sc.nextInt();
            if(i == N-1){
                break;
            }
            i++;
        }
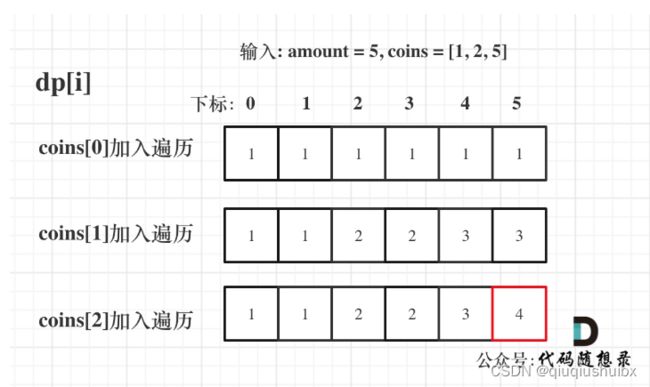
        for(i = 0;i

LeetCode T518 零钱兑换II

题目链接:518. 零钱兑换 II - 力扣（LeetCode）

 

题目思路:

这题我们发现和昨天的目标和是类似的,都是求和为一个数字有多少种方式,所以我们自然而然就能想出他的递推公式的dp[j]+=dp[j-coins[i]];  实际上就是将之前的方法数累加,我们要明确这里

1.dp[j]的含义:

凑成总金额j的货币组合数为dp[j]

2.确定dp数组的递推公式

dp[j]+=dp[j-coins[i]];

3.初始化数化

初始化为0即可,在后面遍历的时候会进行覆盖的

4.确定遍历顺序

这里我们思考一个问题,这题中我们要找的是组合数而不是排列数,那么我们就需要保证这里的coins[0]一定不能在coins[1]之后再出现

所以我们这里使用先物品后背包再合适不过了

5.打印dp数组

题目代码:

class Solution {
    public int change(int amount, int[] coins) {
        int[] dp = new int[amount+1];
        dp[0] = 1;
        for(int i = 0;i

LeetCode T377 组合总和IV

题目链接:377. 组合总和 Ⅳ - 力扣（LeetCode）

 

题目思路:

注意看下面的一个测试用例:(1,3)和(3,1)同时出现了,这说明本题和上一题的唯一区别就是求的是排列数而不是组合数,和数的选取顺序是有关的

1.确定dp数组含义

dp数组的含义是能凑成这个排列数的取值种类有多少种

2.dp数组的递推公式

dp[i] += dp[i-nums[j]];

3.dp数组的初始化

dp[0] = 1;

4.遍历顺序

关键就在于这里,我们使用先遍历背包再遍历物品,这样背包容量为1的遍历了一次全部物品

背包容量为2的也遍历的一次全部物品,所以这里的物品1和物品2的选取不再有序,也就构成了我们的排列数

注:在使用这个递推公式之前记得判断i-nums[j]的大小,避免出现负数

5.打印排错

题目代码:

class Solution {
    public int combinationSum4(int[] nums, int target) {
        int[] dp = new int[target+1];
        dp[0] = 1;
        for(int i = 1;i<=target;i++){
            for(int j = 0;j=nums[j]){
                    dp[i]+=dp[i-nums[j]];
                }
            }
        }
        return dp[target];
    }
}