《动态顺序表》的实现
目录
前言:
认识线性表:
关于顺序表
实现动态顺序表:
顺序表的动态存储定义:
初始化顺序表:
顺序表的销毁:
尾插:
判断是否需要扩容:
总代码:
头插:
打印顺序表:
尾删:
头删:
指定下标插入数据:
指定下标删除:
查找元素下标:
总结:
前言:
从本文开始,我们就正式进入到了《数据结构》这门课程的入门学习,既然是入门,那我们就从较为基础和简单的部分“顺序表“开始我们的学习旅程。本文主要以模拟实现顺序表的增删查改等功能。该部分与我们之前所讲的《动态内存实现通讯录》较为相似,建议在学习此内容前,可以对《通讯录》这一部分进行复习和浏览:运用动态内存实现通讯录(增删查改+排序)-CSDN博客
认识线性表:
线性表是一种数据结构,是由n个具有相同数据类型的数据元素(节点)构成的有限序列。其中,n为线性表的长度,也称为表长。线性表中只有一个开始节点,也只有一个终止节点。线性表的两种常见实现方式是顺序存储和链式存储。
顺序存储是将线性表中的元素顺序存储在一块连续的存储空间(数组)中,通过元素在数组中的下标来访问元素。
链式存储是通过指针将线性表中的元素存储在离散的存储空间中。每个节点都包含元素信息和一个指向下一个节点的指针,通过遍历指针来访问元素。
线性表常见的操作有:插入、删除、查找、遍历等。其中查找操作主要包括按位置查找和按元素值查找。
线性表的应用非常广泛,常见的应用场景包括数组、链表、栈、队列、字符串等。
关于顺序表
顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构,一般情况下采用数组存 储。在数组上完成数据的增删查改。
1.静态顺序表:使用定长数组存储元素
2. 动态顺序表:使用动态开辟的数组存储
静态顺序表只适用于确定知道需要存多少数据的场景。
静态顺序表的定长数组导致N定大了,空间开多了浪费,开少了不够用。所以现实中基本都是使用动态顺序表,根据需要动态的分配空间大小。
下面我们实现动态顺序表
实现动态顺序表:
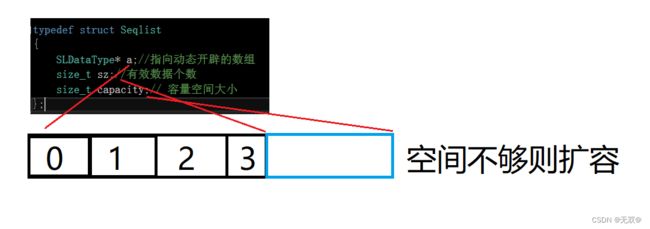
顺序表的动态存储定义:
typedef int SLDataType;
typedef struct Seqlist
{
SLDataType* a;//指向动态开辟的数组
size_t sz;//有效数据个数
size_t capacity;// 容量空间大小
}SL;初始化顺序表:
void SLInit(SL* psl)
{
assert(psl);
psl->a = NULL;
psl->capacity = 0;
psl->sz = 0;
}以上这一部分在我们的通讯录所讲的内容是一致的,如有不懂的还是可以再回顾回顾动态内存实现通讯录的部分,在这里我不做过多的赘述。
顺序表的销毁:
void SLDestory(SL* psl)
{
assert(psl);
free(psl->a);
psl->a = NULL;
psl->capacity = 0;
psl->sz = 0;
}尾插:
对于尾插,顾名思义就是从尾巴插入元素,即在顺序表的数组中,在最后一个位置插入。
但这里我们要考虑一种情况,那就是那我们的预先开辟的空间满了的时候,要先进行扩容操作,再进行尾插,因此便有了以下的函数实现:
判断是否需要扩容:
void SLCheckCapacity(SL* psl)
{
assert(psl);
if (psl->sz == psl->capacity)
{
size_t newcapacity = (psl->capacity == 0) ? 4 : 2 * (psl->capacity);
SLDataType* tmp = (SLDataType*)realloc(psl->a, sizeof(SLDataType)*newcapacity);
if (tmp == NULL)
{
perror("SLCheckCapacity -> realloc");
return;
}
psl->a = tmp;
psl->capacity = newcapacity;
}
}对于以下代码,我们使用了三目操作符,如果我们一开始的空间capacity为0,那么我就给它一个初始空间4。
size_t newcapacity = (psl->capacity == 0) ? 4 : 2 * (psl->capacity);
如果不是并且满了,我们就进行2倍扩容。
这里还要注意的是,realloc是可以对空指针进行扩容的,但是效果相当于malloc开辟空间!!
当扩容操作结束后,就该进行真正的尾插操作。
总代码:
void SLPushBack(SL* psl, SLDataType x)
{
assert(psl);
SLCheckCapacity(psl);
psl->a[psl->sz] = x;
psl->sz++;
}头插:
对于头插我们则需要将a[0]之后的所有元素从后开始,依次往后挪一格,直到腾出a[0]的位置。
所以我们在此可以创建一个指针指向,顺序表最后一个元素,再往前遍历。
顺序表的最后一个元素的下标,熟练之后想都不用想,就是sz - 1!
记住结论!
数组最后一个元素的下标 = 当前元素个数 -1
所以就有了end = psl->sz - 1;
所以总代码为:
void SLPushFront(SL* psl, SLDataType x)
{
assert(psl);
SLCheckCapacity(psl);
size_t end = psl->sz - 1;
while (end)
{
psl->a[end + 1] = psl->a[end];
end--;
}
psl->a[0] = x;
psl->sz++;
}但是对于该算法,如果我们要插入n个数,那么该算法的时间复杂度就是O(N^2)
因此不推荐头插。
而尾插的时间复杂度就直接O(1),所以我们尽量选择尾插而非头插!
打印顺序表:
该函数的实现比较简单,在这里我不做过多的赘述。
void SLPrint(SL* psl)
{
assert(psl);
for (int i = 0; i < psl->sz; i++)
{
printf("%d ", psl->a[i]);
}
printf("\n");
}尾删:
void SLPopBack(SL* psl)
{
assert(psl);
assert(psl->sz>0);
psl->sz--;
}对于该函数的实现,我们的重点就是要注意这个当前数据个数,即SZ的值。
如果我们当前本就没有值,即psl->sz == 0时。
若再进行减减操作,则会在下一次打印的时候出现漏打的现象。
因此我们在这里直接使用assert这种暴力的提醒方式,告诉你函数哪一行出现了错误:
这就是assert的作用!
头删:
对于头删,我们可以与刚刚所讲的头插进行联系,其实就是将第一个元素删除,即a[0]上面的元素被a[1]覆盖,而a[1]被a[2]覆盖,如此以来循环往复,就可以先创建个下标,然后循环遍历。
void SLPopFront(SL* psl)
{
assert(psl);
assert(psl->sz > 0);
int begin = 1;
while (begin < psl->sz)
{
psl->a[begin - 1] = psl->a[begin];
begin++;
}
psl->sz--;
}这里我们和尾删保持一致,先对当前数据个数进行assert断言判断。
指定下标插入数据:
既然是插入数据,那么我们也肯定是要创建指针来挪动数据,再将数据赋值到那个空位置。
代码实现如下:
void SLPushInsert(SL* psl, int pos, SLDataType x)
{
assert(psl);
assert(pos >= 0 && pos <= psl->sz);
int end = psl->sz - 1;
while (end >= pos)
{
psl->a[end + 1] = psl->a[end];
end--;
}
psl->a[pos] = x;
psl->sz++;
}指定下标删除:
该函数实现于上述函数同理:
void SLErase(SL* psl, int pos)
{
assert(psl);
assert(pos >= 0 && pos < psl->sz);
int begin = pos + 1;
while (begin < psl->sz)
{
psl->a[begin - 1] = psl->a[begin];
begin++;
}
psl->sz++;
}查找元素下标:
该函数可用于以上的指定元素删除和插入下标。
具体代码在之前也有讲解,在这里我也不做过多的赘述。
int SLFind(SL* psl, SLDataType x)
{
assert(psl);
for (int i = 0; i < psl->sz; i++)
{
if (psl->a[i] == x)
{
return i;
}
}
return -1;
}总结:
以上我们实现了《顺序表》的初步,说实话该顺序表的实现与之前我们的对通讯录实现动态内存开辟的方式的思维较为类似,下来可以适当的复习通讯录的内容。
记住多练习多画图才可以明白!
“坐而言不如起而行”
Action speak louder than words!
以下是我的Gitee,里面有完整的代码,包括对菜单的实现!
Data structures amd algorithms: 关于数据结构和算法的代码 - Gitee.com