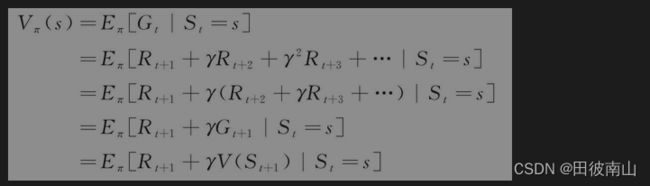强化学习基础

资料

理论资料：《强化学习》邹伟 鬲玲 刘昱杓
《强化学习原理与python实现》肖智清
https://blog.csdn.net/qq_33302004/article/details/115027798
代码资料： https://blog.csdn.net/u011559882/article/details/109015671
https://blog.csdn.net/mbdong/article/details/128266795

（一）基础概念

一、马尔科夫决策过程基础概念

1、马尔科夫性

• 马尔科夫模型的基础是马尔科夫性，马尔科夫性是指当前状态只与上一个状态有关，而与之前状态无关。

2、马尔科夫过程

• 如果随机过程中的每个状态都是符合马尔可夫性的，那么则称这个随机过程为马尔可夫随机过程。
• 马尔可夫过程定义为(S,P)；
• 其中 S是有限状态集， P是状态转移概率（是一个矩阵，描述了S中每一种状态到领一种状态的转移概率）；

3、马尔科夫决策过程

• 在马尔科夫过程中增加动作和奖励就是马尔科夫决策过程;
• 马尔科夫决策过程定义为(S,A,P,R,γ);
• S为有限状态集； A为有限动作集； P为状态转移概率； R为回报函数； γ为折扣因子（用来计算累积回报）；

二、强化学习基础概念

1、智能体和环境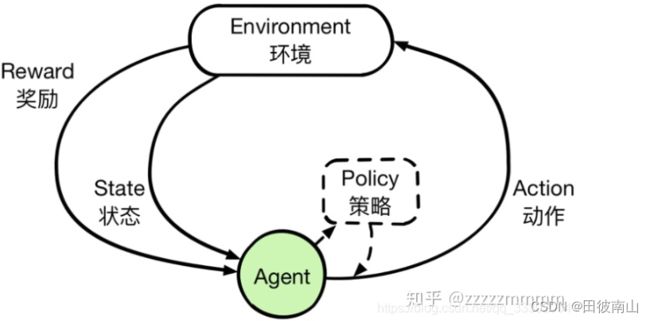

• 智能体根据策略作出动作，环境则作出状态和奖励的反馈
• 马尔科夫决策过程可以用于描述上述强化学习过程

2、马尔科夫决策过程五元组 M=

• 以下面图中这个的内容为例，在4X4的地图中，随机出现在任意一个位置，如何在扣分最少的情况下移动到终点之一。这里简化了一下问题，无论上下左右移动都扣一分，回报的折扣也是1。
  s0->a0->r1->s1->a1->r2->s2->a2->r3->s3
  

（1）状态S

• 在上面的例子中，状态就是1到16，共计16种位置的状态

（2）动作A

• 动作就是上下左右，共计四种移动的动作

（3）转移概率P

• 在不同的状态下，选择不同动作进而转换成不同状态的概率是不同的，将不同状态之间转换的概率称为转移概率。
• 下面这个公式是转移概率的一般定义：
  

（4）策略π

• 策略π则是在s状态下采用动作a的概率，也是我们学习的目标。
• 下面这个公式是转移概率最常被使用的情况，其中出现了两种转移概率，分别是采用策略π的转移概率和通过动作a实现状态转移的概率。基于动作的转移概率是由外部环境决定的，比如在“饱”的状态下进行动作“吃”，大概率状态还是“饱”。而所谓的策略就是在“饱”的状态下，大概率进行动作“不吃”而不是“吃”，进而获得好的状态。
  
• 策略分为两种，确定性策略和非确定性策略。确定性策略典型的就是贪心算法，非确定性就是ε-贪心算法

（5）奖励R

• 奖励R是在获得一个新状态时获得的“评价”，是由外部环境决定的，比如上面走迷宫的例子，移动到另一个状态的奖励都是-1。这个具体的奖励数值环境决定的，但实践中往往也是人为设置进而达到目的，比如设置奖励-1就可以尽量减少移动。
• 这里的奖励是根据状态给出的，而与后面用到的动作状态奖励和策略奖励不同。

（6）折扣γ与回报G

• 根据一个策略则可以获得一系列S（只考虑确定性策略），根据一系列状态S可以获得一系列奖励R，而综合这些奖励则可以计算回报G。
• 不同的策略可以获得不同的回报，比较回报即可比较策略的好坏。为了便于比较，增加了一个折扣系数。否则会都趋于无穷。
• G针对的是未来的一系列状态
  

3、状态值函数和动作-状态值函数

• G函数的定义有一个缺陷，策略未必是确定性的，如果是非确定性的则要考虑不同的动作，而且在不同状态转移的过程中也未必是百分之百的。综合这两点可知一个状态出发可能会有若干状态轨迹，所以要引入期望函数，进而定义了值函数。

• 针对状态和状态-动作的不同情况，将值函数分为状态价值函数V和动作状态价值函数Q，这两种值函数都是针对G的期望。

（1）状态值函数V

在上面那个迷宫的例子中，通过状态价值函数可以得到下面这个表，先不考虑如何获得这个表。只要获得这个表，无论随机出现在哪里都可以选择自己周边奖励绝对值最小的路径作为自己的下一个状态，最后就会尽快到达终点。比如出现在左下角，可以选择向上和向左尽快到达终点。

迭代公式
状态价值函数可以通过定义推导出一个迭代公式

（2）动作-状态值函数Q

迷宫的例子可以无论选择上下左右都可以确定到达对应状态，但是吃饭“饱”“饿”的例子就无法保证切换状态。那么我们就要使用动作-状态价值函数，在当前状态下选择价值最高的动作，而不是状态。

迭代公式

4、贝尔曼期望公式（4种形式）

• 贝尔曼期望公式描述了V和Q之间的关系以及计算式

（1）

（2）

这里涉及到一个新的奖励R，是在S状态时做出动作a动作的价值期望

（3）环境已知情况下，更新V的理论基础（解线性方程和迭代法）

把（2）带入（1）得到（3）

• s和s’分别是t和t+1时刻的状态，如果这两个状态的值相同，则V（s）和V（s‘）相同
  根据上面贝尔曼期望方程的第三个公式得到下式：
  
  
• 上面这个式子说明在转移概率和回报概率已知（环境已知）的情况，则可以直接计算当前的状态价值函数V
• 除了解算线性方程，也可以使用迭代法

（4）

把（3）带入（2）得到（4）

5、贝尔曼最优公式和最优策略（策略改进的基础）

• 上面讲的都是价值函数的定义、性质和关系，但我们的目的还是通过价值函数求出最优策略，下面是价值函数和最优策略的关系和定义。
  
• 根据最优策略获得的价值函数就是最优价值函数和最优动作价值函数，可以通过最优策略获得最优价值函数。反之，最优价值函数在贪心算法的指引下，会得到最优策略。最优策略和价值会最终收敛到一起，这一点成为了策略改进的基础。

（二）如何获得最优策略

• 最优策略是分为两步进行的，策略评估和策略改进。策略评估主要是通过价值函数，策略改进主要通过贪心策略。
• 至于如何获得价值函数有两种思路，一种是通过解线性方程，这种方法计算量大，条件多（可逆、全知），另一种就是迭代，常见的有动态规划、蒙特卡洛法、时间差分法。
• 而策略改进的方法就只有一点点改进了，通过在每一个状态选择当前价值最大的动作进行策略改进，改进后会获得新的价值函数，循环往复即可获得最优策略。
  

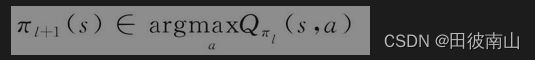
一、动态规划算法

1、策略迭代算法

（1）策略评估

计算V和Q使用贝尔曼期望方程（（3）的迭代形式）：

（2）策略改进

更新策略：
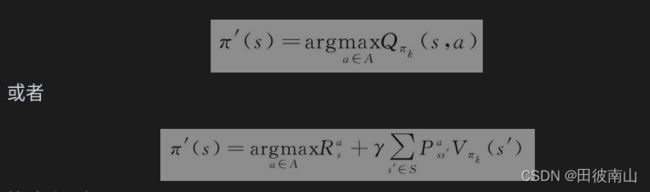基本上在获得最优值函数后，都是使用贪心策略获得策略，之后无变化就不再赘言。

2、值迭代算法

（1）策略评估

• 如果在根据贪心策略修改状态，那么max（Q）=V
• 不进行策略修改，而用行为价值函数Q=状态价值函数V单独进行值迭代
  
  在值函数迭代后，即代表获得最优值函数，再通过贪心算法获得最优策略

3、动态规划的最优值函数代码实现

• 这份代码使用的是值迭代的方法，但是没有用Q的最大值代替V，而是使用策略迭代那里的方法通过状态代价的迭代完成状态价值函数的优化。

# encoding=utf-8
'''
Author: Haitaifantuan
Create Date: 2020-09-07 23:10:17
Author Email: [email protected]
Description: Should you have any question, do not hesitate to contact me via E-mail.
'''
import numpy as np
import copy

#状态是4X4的格子
TOTAL_ROWS = 4       
TOTAL_COLUMN = 4
#动作有4种
TOTAL_ACTIONS_NUM = 4  # 0代表上，1代表右，2代表下，3代表左
ACTION_DICT = {0: '上', 1: '右', 2: '下', 3: '左'}
#初始策略
FOUR_ACTION_PROBABILITY = {'上': 0.25, '右': 0.25, '下': 0.25, '左': 0.25}  # 分别是走上、下、左、右的概率。
#动作->状态
IDX_CHANGE_DICT = {'上': (-1, 0), '右': (0, 1), '下': (1, 0), '左': (0, -1)}  # 左边这个是行的索引的改变，右边这个是列的索引的改变

STOP_CRITERION = 1e-4  #停止标志
GAMMA = 1              #折扣量
REWARD_SETTING = -1    #奖励

def get_current_reward_and_next_state(current_state, action):
    '''
    根据当前的状态，以及行为，计算当前行为的奖励以及下一个状态
    奖励只有0和-1两种
    '''
    # 1、先判断是否到了终点，如果是终点，不管执行什么操作奖励都是0，并且都会回到终点
    row_idx, column_idx = current_state
    if (row_idx == 0 and column_idx == 0):
        return 0, (0, 0)

    if (row_idx == 3 and column_idx == 3):
        return 0, (3, 3)

    # 2、否则的话就计算下下一步的state和reward
    next_row_idx = row_idx + IDX_CHANGE_DICT[action][0]
    next_column_idx = column_idx + IDX_CHANGE_DICT[action][1]

    # 3、再判断是否在边缘，如果是的话，那就回到该位置。
    if next_row_idx < 0 or next_row_idx > TOTAL_ROWS - 1 or next_column_idx < 0 or next_column_idx > TOTAL_COLUMN - 1:
        return REWARD_SETTING, (row_idx, column_idx)      
    else:
        return REWARD_SETTING, (next_row_idx, next_column_idx)


# 初始化状态价值函数V
V = np.zeros((TOTAL_ROWS, TOTAL_COLUMN))

# 开始迭代更新状态价值函数
iteration = 0   #迭代次数
flag = True     #标志
while flag:
    #两个变量都是用来计算是否收敛
    delta = 0
    old_V = copy.deepcopy(V)   #原来的价值函数
    # 遍历每一个状态，对其进行更新
    for row_idx in range(TOTAL_ROWS):
        for column_idx in range(TOTAL_COLUMN):
            new_final_value = 0
            # 根据sutton的《强化学习》第72页公式4.5进行更新
            for each_action in range(TOTAL_ACTIONS_NUM):    #在每个位置都遍历四个动作
                action = ACTION_DICT[each_action]                                                                     #动作
                action_proba = FOUR_ACTION_PROBABILITY[action]                                                        #概率
                current_action_reward, next_state = get_current_reward_and_next_state((row_idx, column_idx), action)  #奖励和状态
                #####关键就是这里，这是状态价值函数的迭代
                new_final_value = new_final_value + action_proba * (1 * (current_action_reward +GAMMA * V[next_state[0]][next_state[1]]))   #对当前动作累积回报
            V[row_idx][column_idx] = new_final_value  #存入回报

    #价值函数是否收敛
    delta = max(delta, abs(old_V - V).max())
    if delta < STOP_CRITERION:  
        flag = False

    iteration += 1

print(V)
print(iteration)

二、蒙特卡洛算法

• 动态规划中是有模型的强化学习算法，即有下面这个公式：
  

• 有模型的算法更偏向于优化，动态规划或者解方程都不需要环境的数据，就像MPC一样，是一种优化算法。而无模型的算法则更像从环境中获得数据并学习。

• 实际问题中往往没有状态转移和回报函数，这个时候可以考虑使用无模型的强化学习算法，无模型的强化学习往往生成一部分数据再进行学习，即通过采样的方法代替策略评估。说白了就是通过大数定律通过回报的平均值等于回报的期望。

1、基于采样的策略估计

（1）初次访问蒙特卡洛方法和每次蒙特卡洛方法

这里所说的均值有两种方法，初次访问蒙特卡洛方法和每次蒙特卡洛方法。

（2）迭代形式

如果每个都计算，存储数据太多，可以写成迭代形式：
V本身就是G的期望

（3）用状态-动作价值函数Q代替状态价值函数V

• 因为要通过行为状态价值函数得到策略，所以要估计的应该是行为状态价值函数，使用下面这个公式
  
• 因为基于采样的蒙特卡洛没有马尔科夫性，所以无法从V到Q，只能直接估计Q
• 整个计算过程都与V的无异

2、策略提升

• 因为数据刚开始往往不全，要采用有探索性的策略
• 基于采样的Q估计和不确定性策略一起组成蒙特卡洛方法
• 这里采用的是在线蒙特卡洛算法

3、蒙特卡洛方法分类

在线和离线的区别就在与产生数据的策略和要优化的策略是否是同一个策略

（1）在线蒙特卡洛方法

（2）离线蒙特卡洛方法

4、蒙特卡洛算法的代码实现

这里的代码只实现了值函数的计算，所以无所谓在线与离线，是每次访问类型。因为针对的是迷宫例子，所以动作的奖励都相同

# encoding=utf-8
'''
Author: Haitaifantuan
Create Date: 2020-09-08 23:47:11
Author Email: [email protected]
Description: Should you have any question, do not hesitate to contact me via E-mail.
'''
import numpy as np
import random
import time
import matplotlib.pyplot as plt
from matplotlib.table import Table

# 解决plt显示中文的问题
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False

class Every_Visit_Monte_Carlo_Policy_Evaluation(object):
    def __init__(self):
        self.total_rows = 4             
        self.total_columns = 4
        self.total_action_num = 4    # 0代表上，1代表右，2代表下，3代表左
        self.reward_each_step = -1   #奖励
        self.action_dict = {0: '上', 1: '右', 2: '下', 3: '左'}
        self.reversed_action_dict = {'上': 0, '右':1, '下':2, '左': 3}
        # 分别是走上、下、左、右的概率。随机数命中某个数字如49，那就是向右。随机数只在0-100随机选数字。
        self.four_action_probability = {'上': range(0, 25), '右': range(25, 50), '下': range(50, 75), '左': range(75, 100)}
        self.idx_change_dict = {'上': (-1, 0), '右': (0, 1), '下': (1, 0), '左': (0, -1)}  # 左边这个是行的索引的改变，右边这个是列的索引的改变
        self.episode = 100000  # 共采集TOTAL_ITERATION幕数据

        # 初始化状态价值函数V


    def get_current_reward_and_next_state(self, current_state, action):
        '''
        根据当前的状态，以及行为，计算当前行为的奖励以及下一个状态
        '''
        row_idx, column_idx = current_state

        # 计算下下一步的state和reward
        next_row_idx = row_idx + self.idx_change_dict[action][0]
        next_column_idx = column_idx + self.idx_change_dict[action][1]

        # 先判断是否到了终点，如果是终点，不管执行什么操作
        # 奖励都是0，并且都会回到终点

        if (next_row_idx == 0 and next_column_idx == 0):
            return 0, (0, 0)

        if (next_row_idx == 3 and next_column_idx == 3):
            return 0, (3, 3)

        # 再判断是否在边缘，如果是的话，那就回到该位置。
        if next_row_idx < 0 or next_row_idx > self.total_rows - 1 or next_column_idx < 0 or next_column_idx > self.total_columns - 1:
            return self.reward_each_step, (row_idx, column_idx)
        else:
            return self.reward_each_step, (next_row_idx, next_column_idx)


    def generate_initial_state(self, total_rows, total_columns):
        row_idx = random.randint(0, total_rows - 1)
        column_idx = random.randint(0, total_columns - 1)

        while (row_idx == 0 and column_idx == 0) or (row_idx == 3 and column_idx == 3):
            row_idx = random.randint(0, total_rows - 1)
            column_idx = random.randint(0, total_columns - 1)

        return (row_idx, column_idx)


    def generate_one_episode_data(self, init_state):  #根据状态随机选择动作，输出状态、动作、奖励
        one_episode_data = []
        current_state = init_state
        while not ((current_state[0] == 0 and current_state[1] == 0) or (current_state[0] == 3 and current_state[1] == 3)):
            # 根据概率产生一个动作
            rand_int = random.randint(0, 99)
            for each in self.four_action_probability.items():
                if rand_int in each[1]:
                    action = each[0]
                    break

            # 根据要走的动作得到奖励以及获取下一个状态
            reward, next_state = self.get_current_reward_and_next_state(current_state, action)
            # （当前状态，当前行为，当前行为的奖励）
            one_episode_data.append((current_state, self.reversed_action_dict[action], reward))

            current_state = next_state

        # while循环出来的时候，最后一个terminal状态没加进去。
        one_episode_data.append((current_state, None, None))

        return one_episode_data


    def fire_calculation(self):
        # 计算“状态价值”
        # 创建一个字典保存出现的状态以及奖励
        begin_time = time.time()

        episode_record_dict = {}             #生成的数据的记录
        final_state_reward_dict = {}         #最终的状态的奖励字典
        final_state_count_dict = {}          #最终的状态的次数字典
        for episode in range(self.episode):
            #1、生成数据
            # 随机生成一个起始状态
            init_state = self.generate_initial_state(self.total_rows, self.total_columns)
            # 生成一幕数据
            current_generated_episode = self.generate_one_episode_data(init_state)#当前状态、随机动作、奖励
            episode_record_dict[episode] = current_generated_episode      #数据存储
            #2、使用数据
            #2.1 将数据存入timeStep_state_reward_dict
            # 对这幕数据进行遍历，然后将出现过的状态进行统计
            timeStep_state_reward_dict = {}  # 记录每一个状态当前的总共的reward
            for timeStep, eachTuple in enumerate(current_generated_episode):
                # 先判断是不是到了终点，如果是的话就跳出循环
                if timeStep == len(episode_record_dict[episode])-1:
                    break

                # 将state和timeStep组合成字符串，方便作为dict的key
                timeStep_state_combination = str(timeStep) + str(eachTuple[0][0]) + str(eachTuple[0][1])

                # 对state_action_reward_dict()里的所有的key都累加当前的reward。
                for key in timeStep_state_reward_dict.keys():
                    timeStep_state_reward_dict[key] += eachTuple[2]

                # 检测当前这一幕该状态和动作组合是否出现过
                if timeStep_state_combination not in timeStep_state_reward_dict.keys():
                    # 如果不存在在timeStep_state_reward_dict.keys()里，那就把它加进去。
                    # 其实每一个时间点都会被添加进去，因为这是“每次访问型蒙特卡罗策略估计”。
                    timeStep_state_reward_dict[timeStep_state_combination] = eachTuple[2]

            # 2.2 将该募最后统计到总的变量里。
            for timeStep_state, in timeStep_state_reward_dict.items():
                # 把timeStep剥离开，取出state
                state = timeStep_state[-2:]
                if state not in final_state_reward_dict.keys():  #如果此状态是第一次出现
                    final_state_reward_dict[state] = reward  # 将该状态-动作计数设为reward
                    final_state_count_dict[state] = 1  # 将该状态-动作计数设为1
                else:
                    # 否则说明其他幕中出现过该状态，并且曾经统计到final_state_action_reward_dict和final_state_action_count_dict变量里面
                    # 直接累加就好了。
                    final_state_reward_dict[state] += reward
                    final_state_count_dict[state] += 1

            if episode % 100 == 0:
                print("第{}个episode已完成=====已花费{}分钟".format(episode, (time.time() - begin_time) / 60))

        # 计算下最终的状态价值
        # 由于是按概率采样，因此可能会导致某些动作-状态没有出现过，这个时候就需要一些方法去解决了。
        # 一种方法是增加采样次数，这种方法相当于是暴力解决。
        # 另一种方法可以参考sutton的《强化学习第二版》的98页的5.4内容
        self.averaged_state_value_dict = {}
        for state, reward in final_state_reward_dict.items():
            self.averaged_state_value_dict[state] = reward / final_state_count_dict[state]   #计算V

        print(self.averaged_state_value_dict)


    def draw_value_picture(self):
        fig, ax = plt.subplots()

        ax.set_axis_off()

        tbl = Table(ax, bbox=[0, 0, 1, 1])

        width = 1.0 / (self.total_columns + 1)
        height = 1.0 / (self.total_rows + 1)

        # 给表格的中间赋值，赋值为该状态的价值
        for row_idx in range(self.total_rows):
            for column_idx in range(self.total_columns):
                if (row_idx == 0 and column_idx == 0) or (row_idx == 3 and column_idx == 3):
                    value = 0
                else:
                    value = self.averaged_state_value_dict[str(row_idx)+str(column_idx)]

                tbl.add_cell(row_idx+1, column_idx+1, width, height,
                             text=value,
                             loc='center', facecolor='white')

        # 给表格行加上索引
        for row_idx in range(self.total_rows):
            tbl.add_cell(row_idx+1, 0, width, height, text=row_idx, loc='right', edgecolor='none', facecolor='none')

        # 给表格列加上索引
        for column_idx in range(self.total_columns):
            tbl.add_cell(0, column_idx+1, width, height/4, text=column_idx, loc='center', edgecolor='none', facecolor='none')

        ax.add_table(tbl)
        plt.show()


obj = Every_Visit_Monte_Carlo_Policy_Evaluation()    #每次访问蒙特卡洛策略估计
obj.fire_calculation()        #开始计算 
obj.draw_value_picture()      #开始画图

三、时间差分算法

1、算法原理

• 用Rt+1+γV(st+1)代替G，
• 蒙特卡罗需要完整未来轨迹，时间差分则只需要一步

• 注意这个图中，是向未来期望价值的计算

2、算法分类

3、代码实现

# encoding=utf-8
'''
Author: Haitaifantuan
Create Date: 2020-09-08 23:47:11
Author Email: [email protected]
Description: Should you have any question, do not hesitate to contact me via E-mail.
'''
import numpy as np
import random
import time


class Q_Learning(object):
    def __init__(self):
        # 创建一个q函数，其实就是Q表格
        # 一共6个状态，每个状态都有合法的action
        # 这个列代表当前所处的状态，行代表即将到达的状态
        self.q_function = np.zeros((6, 6))
        # 这个字典记录了在哪个状态（房间），可以到达哪个状态（房间）
        self.available_action = {0:[4], 1:[3, 5], 2:[3], 3:[1, 2, 4], 4:[0, 3], 5:[1]}
        self.destination_reward = 100
        self.episode = 10000  # 共采集TOTAL_ITERATION幕数据
        self.initial_epsilon = 0.5
        self.epsilon_decay_ratio = 0.90
        self.final_epsilon = 0.01
        self.alpha = 0.8
        self.gamma = 0.9
        print("q_function为：{}".format(self.q_function))
        print("============================================================")


    def generate_initial_state(self):
        state = random.randint(0, 5)
        while state == 0 or state == 5:
            state = random.randint(0, 5)
        return state


    def generate_action_and_get_reward_and_next_state(self, current_state):
        # 使用ε-greedy的方法以及贪婪的方法选取一个动作以及做一个动作并获得回报
        if random.random() < self.epsilon:
            # 根据当前的状态，随机选取一个动作
            next_state = random.choice(self.available_action[current_state])
        else:
            # 找到当前可到达的下一个状态
            available_next_state_list = self.available_action[current_state]
            # 根据可到达的下一个状态，使用贪婪的策略找到使得获得最大收益的那个动作对应的下一个状态
            # 拿到可行的下一个状态的回报
            available_next_state_reward_list = self.q_function[current_state][available_next_state_list]
            # 找到最大的那个回报的索引，如果有多个同样大小的值，就随机选取一个
            max_value = np.max(available_next_state_reward_list)
            indices = list(np.where(available_next_state_reward_list == max_value)[0])
            idx = random.choice(indices)
            # 根据这个索引找到最大回报的下一个状态是什么
            next_state = available_next_state_list[idx]

        # 判断下是否到达4号房间或者5号房间
        if next_state == 4 or next_state == 5:
            reward = 100
            finished_flag = True
        else:
            reward = 0
            finished_flag = False


        return next_state, reward, finished_flag


    def fire_calculation(self):
        # 对每一个episode进行循环
        self.epsilon = self.initial_epsilon

        for episode in range(self.episode):
            # 随机生成一个起始状态
            current_state = self.generate_initial_state()
            finished_flag = False

            while not finished_flag:
                # 使用ε-greedy的方法以及贪婪的方法选取一个动作以及做一个动作并获得回报
                next_state, current_state_reward, finished_flag = self.generate_action_and_get_reward_and_next_state(current_state)

                # 根据下一个状态，使用ε-greedy的方法以及贪婪的方法选取一个动作以及做一个动作并获得回报
                # 这里不需要管finished_flag是否为True，因为我们只是根据next_state拿到next_state情况下最大的下下个状态的奖励值
                next_next_state, next_state_reward, next_state_finished_flag = self.generate_action_and_get_reward_and_next_state(next_state)

                # 根据公式更新q函数
                self.q_function[current_state][next_state] = self.q_function[current_state][next_state] + \
                    self.alpha * (current_state_reward + self.gamma * (next_state_reward) - self.q_function[current_state][next_state])

                current_state = next_state

            # 一个episode结束后更新epsilon的值
            if self.epsilon > self.final_epsilon:
                self.epsilon = self.epsilon * self.epsilon_decay_ratio

            if episode % 3000 == 0:
                print("第{}个episode已经结束".format(episode))
                print("当前的q_function是：{}".format(self.q_function))


    def show_policy(self):
        print("当前的q_function是：{}".format(self.q_function))
        self.policy = {}

        print("策略是：")
        shape = np.shape(self.q_function)
        for current_state in range(shape[0]):
            max_reward_state = np.argmax(self.q_function[current_state])
            self.policy[current_state] = max_reward_state
            if current_state == 4 or current_state == 5:
                continue
            print("如果你在{}号房间，那就往{}号房间走".format(current_state, max_reward_state))



obj = Q_Learning()
obj.fire_calculation()
obj.show_policy()

（三）基于DQN的倒立摆

• 这是一个完整使用gym实现的基于DQN的强化学习应用，使用全连接网络逼近Q函数，使用Q-learning算法

# import required modules
import gym
import random
import numpy as np
import math

import torch
import torch.nn as nn
class Net(nn.Module):
    def __init__(self, n_states, n_actions):
        super().__init__()
        
        self.fc1 = nn.Linear(n_states, 10)
        self.fc2 = nn.Linear(10, n_actions)
        
        self.fc1.weight.data.normal_(0,0.1)
        self.fc2.weight.data.normal_(0,0.1)
        
    def forward(self, inputs):
        x = self.fc1(inputs)
        x = nn.functional.relu(x)
        outputs = self.fc2(x)
        
        return outputs
# define DQN
class DQN:
    def __init__(self, n_states, n_actions):
        # two nets
        self.eval_net = Net(n_states, n_actions)
        self.target_net = Net(n_states, n_actions)
        
        self.loss = nn.MSELoss()
        
        self.optimizer = torch.optim.Adam(self.eval_net.parameters(), lr=0.01)
        
        self.learn_step = 0
        
        self.n_states = 4
        self.n_actions = 2
        
        # define variables for history data storage
        self.history_capacity = 5000
        self.history_data = np.zeros((self.history_capacity, 2*n_states+2)) # state, action, reward, next_state
        self.history_index = 0
        self.history_num = 0
        
    def random_action(self):
        r = random.random()
        if r >= 0.5:
            action = 1
        else:
            action = 0
        
        return action
    
    def choose_action(self, state, epsilon):
        r = random.random()
        if r > epsilon:
            action = self.random_action()
        else:
            state = torch.FloatTensor(state)
            state = torch.unsqueeze(state, 0)
            
            evals = self.eval_net.forward(state)
            action = np.argmax(evals.data.numpy())
            
        return action
    
    # function to calculate reward
    def get_reward(self, state):
        pos, vel, ang, avel = state
        
        pos1 = 1.0
        ang1 = math.pi/9
        
        r1 = 5-10*abs(pos/pos1)
        r2 = 5-10*abs(ang/ang1)
        if r1 < -5.0:
            r1 = -5.0
        if r2 < -5.0:
            r2 = -5.0
            
        return r1+r2
    
    # definition of game end
    def gg(self, state):
        pos, vel, ang, avel = state
        
        bad = abs(pos) > 2.0 or abs(ang) > math.pi/4
        
        return bad

	# function to store history data    
    def store_transition(self, prev_state, action, reward, state):
        transition = np.hstack((prev_state, action, reward, state))
        self.history_data[self.history_index] = transition
        
        self.history_index = (self.history_index + 1)%self.history_capacity
        
        if self.history_num < self.history_index:
            self.history_num = self.history_index

	# learn
    def learn(self):
        # random choose a batch of sample indices
        indices = np.random.choice(self.history_num, 64)
        
        samples = self.history_data[indices, :]
        state = torch.FloatTensor(samples[:, 0:self.n_states])
        action = torch.LongTensor(samples[:, self.n_states:self.n_states+1])
        reward = torch.FloatTensor(samples[:, self.n_states+1:self.n_states+2])
        next_state = torch.FloatTensor(samples[:, self.n_states+2:])

        q_eval = self.eval_net(state).gather(1, action)
        q_next = self.target_net(next_state)
        
        # calculate target q values
        q_target = 0.9*q_next.max(1).values.unsqueeze(1) + reward
        
        loss = self.loss(q_eval, q_target)
        
        # backward training
        self.optimizer.zero_grad()
        loss.backward()
        self.optimizer.step()
        
        self.learn_step += 1
        
        # update target net every 50 learn steps
        if self.learn_step % 50 == 0:
            self.target_net.load_state_dict(self.eval_net.state_dict())
# create cartpole model
env = gym.make('CartPole-v1', render_mode='human')

# reset state of env
state, _ = env.reset()

# crate DQN model
model = DQN(4, 2)

# parameters
max_sim_step = 100000

# simulate
for i in range(max_sim_step):
    env.render()
    #选择动作
    epsilon = 0.7 + i / max_sim_step * (0.95 - 0.7)
    action = model.choose_action(state, epsilon)
    
    prev_state = state
    state, reward, _, _, _ = env.step(action)
    
    reward += model.get_reward(state)

    model.store_transition(prev_state, action, reward, state)

	# perform model learning every 10 simulation steps    每10个模拟步骤进行模型学习
    if i>1000 and i%10 == 0:
        model.learn()   

    if model.gg(state):
        state, _ = env.reset()

env.close()