Unity使用mesh绘制模型

基本概念

首先要知道模型是如何产生的?

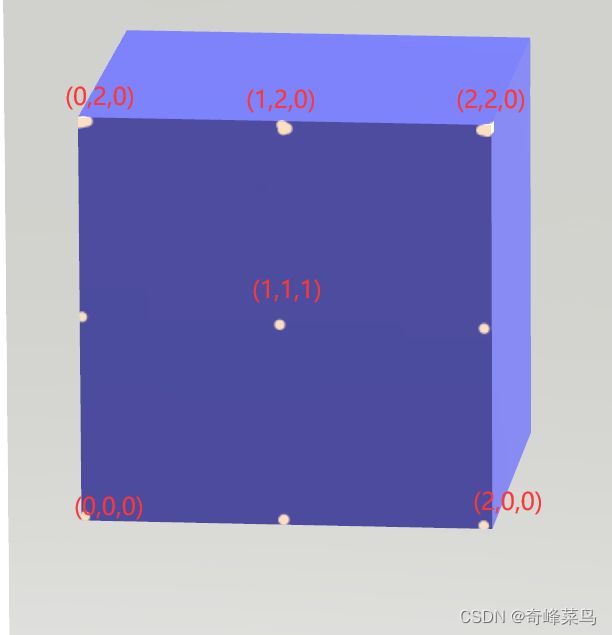
比如说我们在一个3*3的空间创建这样9个点(vector3)

 这9个点构成了我们模型的范围

三点成三角，三角呈面

 然后由面绘制出体

用这种方法可以绘制我们想要的图形

理论转为实践!

第一步：绘制点

先将刚才的正方体转为代码吧

可以看到我们的正方体有9个点(3*3)

所以,我们建立一个X和Y都为3的数组来包含这9个顶点

  /// 

    /// 矩阵x，y位置
    /// 
    public Vector3[,] Out;

    private void OnEnable()
    { Generate();
    }

    private void Generate()
    {
        Out=new Vector3[3,3];//几行?几列?
        for (int x = 0; x < 3; x++)
        {
            for (int y = 0; y < 3;y++)
            {
                Out[x, y] = new Vector3(x, y,0);
            }
         
        }
    }

 这个方法帮我们为这个数组附了值,从(0,0,0)到(2,2,0)

顶点已经构建好了.如何证明(可视化)呢?

    private void OnDrawGizmos()
    {
        Gizmos.color = Color.black;
        for (int x = 0; x < 3; x++)
        {
            for (int y = 0; y < 3;y++)
            {
                Gizmos.DrawSphere(transform.TransformPoint(Out [x,y]),0.1f);
            }
        }
    }

OnDrawGizmos api帮助我们解决这个问题

这个方法在编辑模式里也会反复执行,为我们绘制顶点(因为在编辑模式也运行,所以现在这样写不启动的话会报空)

运行!

 这9个顶点如我们所想被绘制出来了

顶点位置确认无误，我们让当前的这个cube持有这些顶点

    private void Generate()
    {   
       
        Out=new Vector3[3,3];//几行?几列?
        for (int x = 0; x < 3; x++)
        {
            for (int y = 0; y < 3;y++)
            {
                Out[x, y] = new Vector3(x, y,0);   Debug.Log(x.ToString()+y.ToString());
            }
        }
        mesh= GetComponent().mesh;
        mesh.Clear();//清理原顶点数据
        mesh.vertices = TwoD_1(Out);//赋予新的顶点数据
    }
    
    public static T[] TwoD_1(T[,] obj)
    {
        T[] obj2 = new T[obj.Length];
        for (int i = 0; i < obj.Length; i++)
            obj2[i] = obj[i / obj.GetLength(1), i % obj.GetLength(1)];
        return obj2;
    }

进行到这里,我们在运行程序,发现物体已经从正方体变为正方形了(因为目前的顶点数据z轴都为0)

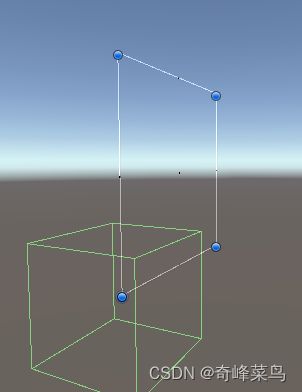
第二步：三点连为三角形

在上一步骤中,我们已经成功将顶点数据保存了

在这里,我们只要调用顶点数据即可

        mesh.triangles = new int[] {a,b,c};

这段代码意为绘制一个三角形,顶点为a,b,c

 

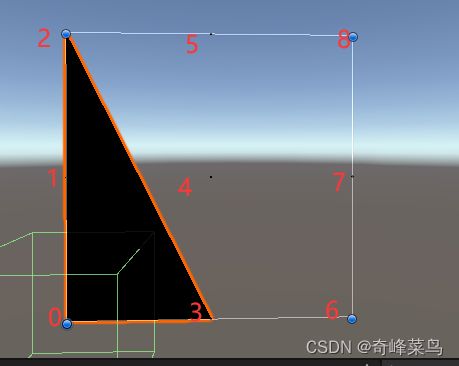
 注意：这样绘制的三角形只有一面（跑到后面就看不到了）

顺时针绘制三角形正面可见，逆时针绘制背面可见

快速知道自己的三角形正面可见或正面可见的方法是：

从第一个顶点到第三个顶点以顶点1~顶点2距离为半径顺时针画圆是否经过第二个顶点。如果经过就是正面可见，否则背面可见

如果要绘制另一面，需要将数组反转

比如【0，2，3】绘制一个正面可见的三角形，【3，2，0】绘制一个背面可见的三角形

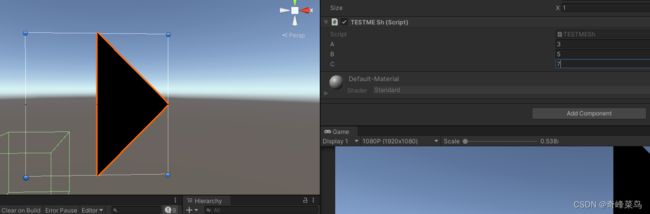
第三步：多个三角形构建一个面

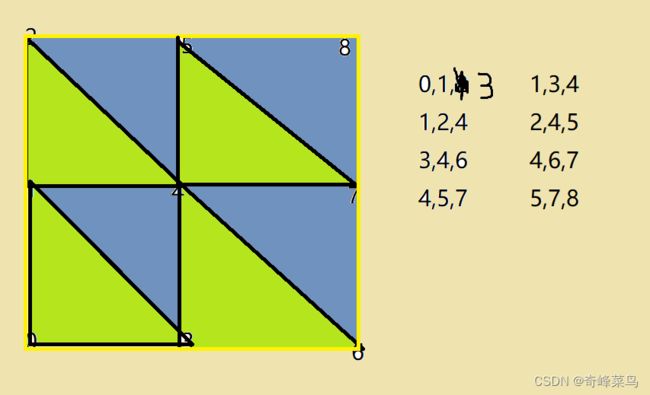
现在,我们遍历三角形将这个面铺满

 找到规律转为算法写到脚本

        int[] Triangles = new int[(3-1)*(3-1)*3*2];//根据顶点可知2x2个三角形可以铺满这个正方形
        int T_x = 0;//第一个三角形的第一个顶点坐标为0
        for (int i = 0; i < 12;)//遍历三角形
        {
            Triangles[i++] = T_x;
            Triangles[i++] = T_x + 1;
            Triangles[i++] = T_x + 3;
            T_x++;//开始构建下一个三角形
            if ((T_x+1)%3==0)//顶点不能是3的倍数,因为3在最上面一行
            { 
                T_x++;
            }
        }

       T_x = 1;
        for (int i = 12; i < 24; )
        {
         
            Triangles[i++] = T_x;
            Triangles[i++] = T_x + 3;
            Triangles[i++] = T_x + 2;
            T_x++;//开始构建下一个三角形
            if ((T_x)%3==0)//顶点不能是3的倍数,因为3在最上面一行
            { 
                T_x++;
            }
        }
        mesh.triangles = Triangles;
        

 第四步：多面成体

现在，我们已经成功做出一面，学mesh当然不只为做一面了，肯定是为了做模型

将多面拼起来就可以获得模型

现在重新改点坐标，做一个立体模型,就像这样

 

 计算每一个面所需要的三角形位置,拼接到数组就可以实现了

如果模型黑色或透明,有两种方式:

①为mesh贴uv，然后附材质球。材质球就会根据uv来渲染

uv数组的大小应该与顶点相同，他将会把每4个顶点视为一个正方形（面）

然后你就可以为面附贴图

        for (int i = 0; i < uvs.Length; i += 3)
        {
            //正常贴图
            uvs[i] = new Vector2(0, 0);
            uvs[i + 1] = new Vector2(0, 1);
            uvs[i + 2] = new Vector2(1, 1);
        }     mesh.uv = uvs;

 ②写一个shader，获取顶点和法线直接渲染，然后将shader附给材质，再贴给材质球

// Upgrade NOTE: replaced 'mul(UNITY_MATRIX_MVP,*)' with 'UnityObjectToClipPos(*)'

Shader "Custom/NewSurfaceShader"
{
 
    Properties{
        _Color("ColorRange",Color)=(1.0,1.0,1.0,1.0)
           
        }
   SubShader{
      
      Pass{
          CGPROGRAM
          #pragma vertex vert
          #pragma fragment frag
        fixed4 _Color;


          
          struct a2v
          {
              float4 vertex : POSITION;
              float3 normal : NORMAL;
            //  float4 texcoord : TEXCOORD0;
          };
          
          struct v2f
          {
              float4 pos:SV_POSITION;
              fixed3 color: COLOR0;
          };

v2f vert(a2v v)
{
    v2f o;
    o.pos=UnityObjectToClipPos(v.vertex);
    o.color=v.normal*0.5f+fixed3(0.5,0.5,0.5);
    return o;
}
          fixed4 frag(v2f i):SV_Target{
fixed3 c=i.color;
              c*=_Color.rgb;

              return  fixed4(c,1.0);
          }
          
          ENDCG
          }
     
       
       }
}

参考文章：

(38条消息) Unity网格篇Mesh（一）_类人_猿的博客-CSDN博客_unity 网格

(38条消息) C#数组维度转换：一维数组&二维数组&三维数组相互转换_水为痕的博客-CSDN博客_c# 一维数组转二维数组