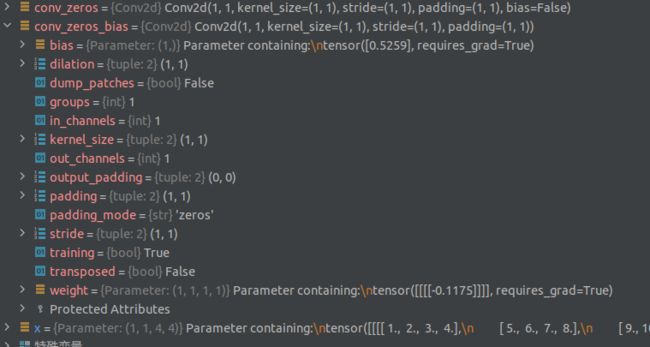
pytorch 中 nn.Conv2d 解释
1. pytorch nn.Con2d 中填充模式
torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode=‘zeros’, device=None, dtype=None)
1.1 padding 参数的含义
首先 ,padd = N, 代表的是 分别在 上下,左右 这四个方向上都填充 N 个数值;
举例, 如果 padd = N = 1, 那么代表是 在 上下左右 都填充1 个数值, 那么 此时原始的输入矩阵便会增加 2* N 行, 2* N 列, 这里便是增加了 2行2 列;
这样 我们 就会理解, 为什么 计算2维 卷积的输出的时候,
是
[ i + 2 ∗ p a d d i n g − k e r n e l s i z e ] 下取整 / s t r i d e + 1 ; [ i + 2*padding -kernel_{size} ]下取整 / stride + 1; [i+2∗padding−kernelsize]下取整/stride+1;
1.2 padding_mode 参数
该参数便是规定了, padding 的时候 如何生成这些padding 的具体数值,
即以何种方法 生成padding 数值;
PyTorch二维卷积函数 torch.nn.Conv2d() 有一个“padding_mode”的参数,可选项有4种:‘zeros’, ‘reflect’,
‘replicate’ or ‘circular’,其默认选项为’zeros’,也就是零填充。这四种填充方式到底是怎么回事呢?
padding_mode (string, optional): `'zeros'`, `'reflect'`,
`'replicate'` or `'circular'`. Default: `'zeros'`
为了直观的观察这4种填充方式,我们定义一个1*1卷积,并将卷积核权重设置为1,这样在进行不同填充方式的卷积计算后,我们即可得到填充后的矩阵。本例中我们生成一个由1~16组成的4*4矩阵,对其进行不同填充方式的卷积计算。
In [51]: x = torch.nn.Parameter(torch.reshape(torch.range(1,16),(1,1,4,4)))
In [52]: x
Out[52]:
Parameter containing:
tensor([[[[ 1., 2., 3., 4.],
[ 5., 6., 7., 8.],
[ 9., 10., 11., 12.],
[13., 14., 15., 16.]]]], requires_grad=True)
1.‘zeros’
'zeros’就是最常见的零填充,即在矩阵的高、宽两个维度上用0进行填充,填充时将在一个维度的两边都进行填充。
In [53]: conv_zeros = torch.nn.Conv2d(1,1,1,1,padding=1,padding_mode='zeros',bias=False)
In [54]: conv_zeros
Out[54]: Conv2d(1, 1, kernel_size=(1, 1), stride=(1, 1), padding=(1, 1), bias=False)
In [55]: conv_zeros.weight = torch.nn.Parameter(torch.ones(1,1,1,1))
In [56]: conv_zeros.weight
Out[56]:
Parameter containing:
tensor([[[[1.]]]], requires_grad=True)
In [57]: conv_zeros(x)
Out[57]:
tensor([[[[ 0., 0., 0., 0., 0., 0.],
[ 0., 1., 2., 3., 4., 0.],
[ 0., 5., 6., 7., 8., 0.],
[ 0., 9., 10., 11., 12., 0.],
[ 0., 13., 14., 15., 16., 0.],
[ 0., 0., 0., 0., 0., 0.]]]], grad_fn=)
x = torch.nn.Parameter(torch.reshape(torch.range(1,16),(1,1,4,4)))
conv_zeros = torch.nn.Conv2d(1,1,1,1,padding=1,padding_mode='zeros',bias=False)
conv_zeros_bias = torch.nn.Conv2d(1,1,1,1,padding=1,padding_mode='zeros',bias=True)
conv_zeros.weight = torch.nn.Parameter(torch.ones(1,1,1,1))
conv_zeros(x)
tensor([[[[ 0., 0., 0., 0., 0., 0.],
[ 0., 1., 2., 3., 4., 0.],
[ 0., 5., 6., 7., 8., 0.],
[ 0., 9., 10., 11., 12., 0.],
[ 0., 13., 14., 15., 16., 0.],
[ 0., 0., 0., 0., 0., 0.]]]],
grad_fn=<MkldnnConvolutionBackward>)
conv_zeros_bias(x)
tensor([[[[ 0.5259, 0.5259, 0.5259, 0.5259, 0.5259, 0.5259],
[ 0.5259, 0.4084, 0.2909, 0.1734, 0.0559, 0.5259],
[ 0.5259, -0.0616, -0.1791, -0.2966, -0.4141, 0.5259],
[ 0.5259, -0.5316, -0.6492, -0.7667, -0.8842, 0.5259],
[ 0.5259, -1.0017, -1.1192, -1.2367, -1.3542, 0.5259],
[ 0.5259, 0.5259, 0.5259, 0.5259, 0.5259, 0.5259]]]],
grad_fn=<MkldnnConvolutionBackward>)
那么问题来了, 设置 bias 是否为 True,
同样的 输入, 同样的 可学习参数权重,
只要设置 bias , 将会得到不同的 结果?
那么 bias 到底 起到什么作用呢?
2.‘reflect’
'reflect’是以矩阵边缘为对称轴,将矩阵中的元素对称的填充到最外围。
In [58]: conv_reflect = torch.nn.Conv2d(1,1,1,1,padding=1,padding_mode='reflect',bias=False)
In [59]: conv_reflect.weight = torch.nn.Parameter(torch.ones(1,1,1,1))
In [60]: conv_reflect(x)
Out[60]:
tensor([[[[ 6., 5., 6., 7., 8., 7.],
[ 2., 1., 2., 3., 4., 3.],
[ 6., 5., 6., 7., 8., 7.],
[10., 9., 10., 11., 12., 11.],
[14., 13., 14., 15., 16., 15.],
[10., 9., 10., 11., 12., 11.]]]], grad_fn=)
3.‘replicate’
'replicate’将矩阵的边缘复制并填充到矩阵的外围。
In [61]: conv_reflect = torch.nn.Conv2d(1,1,1,1,padding=1,padding_mode='replicate',bias=False)
In [62]: conv_reflect.weight = torch.nn.Parameter(torch.ones(1,1,1,1))
In [63]: conv_replicate(x)
Out[63]:
tensor([[[[ 1., 1., 2., 3., 4., 4.],
[ 1., 1., 2., 3., 4., 4.],
[ 5., 5., 6., 7., 8., 8.],
[ 9., 9., 10., 11., 12., 12.],
[13., 13., 14., 15., 16., 16.],
[13., 13., 14., 15., 16., 16.]]]], grad_fn=)
4.‘circular’
顾名思义,'circular’就是循环的进行填充,怎么循环的呢?先看例子:
In [64]: conv_reflect = torch.nn.Conv2d(1,1,1,1,padding=1,padding_mode='circular',bias=False)
In [65]: conv_reflect.weight = torch.nn.Parameter(torch.ones(1,1,1,1))
In [66]: conv_circular(x)
Out[66]:
tensor([[[[16., 13., 14., 15., 16., 13.],
[ 4., 1., 2., 3., 4., 1.],
[ 8., 5., 6., 7., 8., 5.],
[12., 9., 10., 11., 12., 9.],
[16., 13., 14., 15., 16., 13.],
[ 4., 1., 2., 3., 4., 1.]]]], grad_fn=)
如果将输入矩阵从左到右,从上到下进行无限的重复延伸,即为下面这种形式:
tensor([[[[ 1., 2., 3., 4., 1., 2., 3., 4., 1., 2., 3., 4.],
[ 5., 6., 7., 8., 5., 6., 7., 8., 5., 6., 7., 8.],
[ 9., 10., 11., 12., 9., 10., 11., 12., 9., 10., 11., 12.],
[13., 14., 15., 16., 13., 14., 15., 16., 13., 14., 15., 16.],
[ 1., 2., 3., 4., 1., 2., 3., 4., 1., 2., 3., 4.],
[ 5., 6., 7., 8., 5., 6., 7., 8., 5., 6., 7., 8.],
[ 9., 10., 11., 12., 9., 10., 11., 12., 9., 10., 11., 12.],
[13., 14., 15., 16., 13., 14., 15., 16., 13., 14., 15., 16.],
[ 1., 2., 3., 4., 1., 2., 3., 4., 1., 2., 3., 4.],
[ 5., 6., 7., 8., 5., 6., 7., 8., 5., 6., 7., 8.],
[ 9., 10., 11., 12., 9., 10., 11., 12., 9., 10., 11., 12.],
[13., 14., 15., 16., 13., 14., 15., 16., 13., 14., 15., 16.]]]])
image.png
看出来了吗?如果无限延伸的话这样就是对原始的4*4矩阵的循环,上面的矩阵就是在高和宽维度上都填充4个单位的结果,如果只填充1个单位,那就只截取填充一个单位后的矩阵:
image.png
这就是例子中只填充1个单位的结果。
refer
https://www.jianshu.com/p/a6da4ad8e8e7