算法刷题2【剑指offer系列之字符串】

2020.05.28

1、字符串的全排列

输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。
输入一个字符串,长度不超过9(可能有字符重复),字符只包括大小写字母。
思路：这道题在华为2020年春招的笔试题考了原题。
（1）首先考虑字符不重复的情况
输入：abc
输出：abc acb bac bca cab cba
考虑把复杂的问题分解成小的问题。比如，**把一个字符串看成由两部分组成：第一部分是它的第一个字符；第二部分是后面的所有字符。**而我们求整个字符串的排列，可以看成两步。
第一步求所有可能出现在第一个位置的字符，即把第一个字符和后面所有的字符交换（全排列）。
第二步是固定第一个字符，求后面所有字符的排列。这时候我们仍把后面的所有字符分成两个部分：后面字符的第一个字符，以及这个字符之后的所有字符。然后把第一个字符和它后面的所有字符交换。（相当于是子问题）
这里需要注意的是在递归交换下一个位置以后，还需要多一次交换。第二个swap的目的是使得字符数组的顺序回到进入递归前的状态，这样才不会影响后面的遍历顺序。因为在第一次交换后进入递归运算的时候，字符数组的顺序改变了，例如“abc”， i = 0时对应‘a’，j = 1时对应 ‘b’，进行一次交换，此时的字符数组的顺序为 “bac”，从递归返回时，顺序依然是“bac”，则进行第二次交换使得 “bac” -> “abc”，这样在后续才可以和j=2进行交换，即’a’与’c’的交换，确保不会落下某一种情况。
（2）接下来考虑字符重复的情况： 比如

输入：acc 
输出：acc cac cca

也就是后面两个c是重复的，我们可以先不管重复的，出了结果再进行去重，但是这样的效率会比较低，因为产生了很多没有必要的结果。

public class AllPermutation {
   
    public static void main(String[] args) {
   
        AllPermutation permutation=new AllPermutation();
        String str="abc";
        ArrayList<String> strings = permutation.Permutation(str);
        for (String s:strings){
   
            System.out.println(s);
        }
    }
    ArrayList<String> res = new ArrayList<>();
    public ArrayList<String> Permutation(String str) {
   
        if (str == null || str.length() == 0) {
   
            return res;
        }
        char[] chars = str.toCharArray();
        judge(chars, 0);
        //使用treeSet完成去重（aa,aa只输出一个）+按字典排序
        TreeSet<String> set=new TreeSet<String>(new Comparator<String>() {
   
            @Override
            public int compare(String o1, String o2) {
   
                return o1.compareTo(o2);
            }
        });
        for (String temp:res){
   
            if (!set.contains(temp)){
   
                set.add(temp);
            }
        }
        return new ArrayList<>(set);
    }

    /**
     * 遍历到的字符串位置
     *
     * @param chars
     * @param i
     */
    private void judge(char[] chars, int i) {
   
        if (i == chars.length) {
   
            res.add(String.valueOf(chars));
            return;
        }
        for (int j=i;j<chars.length;j++){
   
            swap(chars,i,j);
            //递归
            judge(chars,i+1);
            //回到递归前的状态
            swap(chars,i,j);

        }
    }

    private void swap(char[] chars, int i, int j) {
   
        char temp=chars[i];
        chars[i]=chars[j];
        chars[j]=temp;
    }

}

**更好的方法：**包含重复元素的问题，只需要将遍历到的每一个字符，放入set集合中即可。举个例子:对abb，第1个数a与第2个数b交换得到bab，然后变回abb，考虑第1个数与第3个数交换，此时由于第3个数等于第2个数，所以第1个数就不再用与第3个数交换了，这个逻辑可以使用set来判断，j遍历的时候判断字符是否已经出现过。最后我们再考虑bab，它的第2个数与第3个数交换可以解决bba。此时全排列生成完毕，但是题目要求字典序输出，因此我们还需要进一步处理。

public class Test {
   

    public static void main(String[] args) {
   
        Test test=new Test();
        ArrayList<String> acc = test.Permutation("acc");
        PrintUtils.printList(acc);
    }

    /**
     * res一定要放在外面，不然每次递归都初始化，是错的
     */
    ArrayList<String> res = new ArrayList<>();
    public ArrayList<String> Permutation(String str) {
   
        if (str == null || str.length() == 0) {
   
            return res;
        }
        char[] chars = str.toCharArray();
        judge(chars, 0);
        //还需要res进行按照字典序输出
        Collections.sort(res, new Comparator<String>() {
   
            @Override
            public int compare(String o1, String o2) {
   
                return o1.compareTo(o2);
            }
        });
        return res;
    }

    /**
     * @param chars
     * @param i
     * @return
     */
    private void judge(char[] chars, int i) {
   
        int len = chars.length;
        if (i == len) {
   
            res.add(String.valueOf(chars));
            return;
        }
        HashSet<Character> set = new HashSet<>();
        /**
         * 对abb，第一个数a与第二个数b交换得到bab，然后考虑第一个数与第三个数交换，
         * 此时由于第三个数等于第二个数，所以第一个数就不再用与第三个数交换了。
         * 再考虑bab，它的第二个数与第三个数交换可以解决bba。此时全排列生成完毕！
         */
        for (int j = i; j < len; j++) {
   
            if (!set.contains(chars[j])) {
   
                set.add(chars[j]);
                swap(chars, i, j);
                judge(chars, i + 1);
                swap(chars, i, j);
            }
        }
    }

    private void swap(char[] chars, int i, int j) {
   
        char temp = chars[i];
        chars[i] = chars[j];
        chars[j] = temp;
    }

扩展1：求字符串的所有组合（全部子序列）

思路:因为ab和ba是算一个组合的，所以其实求字符串的所有组合就是相当于求字符串的所有子序列。比如abc，子序列有"",a,b,c,ab,ac,bc,abc
这种字符串的递归特别注意的是结束条件，必须是string.length，不需要-1.因为这样才是将最后的那个字符也算进去。还有就是本题中的递归函数传入的参数还是有点难想，需要包括整个字符数组（字符串），到了第i个字符、当前的结果。而上题只需要字符数组和遍历到的位置，结果是记录到全局的res中。

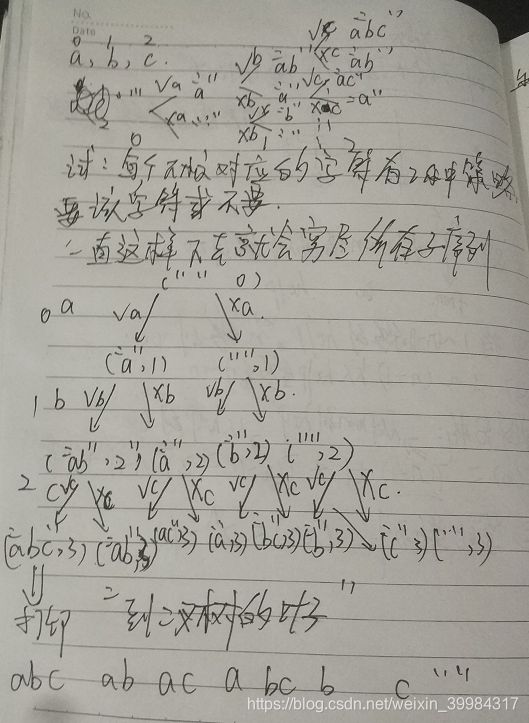
public class PrintAllSubsquences {
   
    public static void main(String[] args) {
   
        //一开始的中间结果为空
        process("abc".toCharArray(),0,"");
        PrintUtils.printList(res);
    }

    private static ArrayList<String> res = new ArrayList<>();

    /**
     * @param chars 输入的字符数组(字符串)
     * @param i     遍历到的位置
     * @param temp  字符串的中间结果
     */
    public static void process(char[] chars, int i, String temp) {
   
        if (chars.length == i) {
   
            res.add(temp);
            return;
        } else {
   
            //每个字符有两个决策，要或者不要
            //1.要
            process(chars, i + 1, temp + chars[i]);
            //2、不要
            process(chars, i + 1, temp);
        }

    }

}

扩展2、输入一个含有8个数字的数组，判断有没有可能把这8个数字分别放到正方体的8个顶点上，使得正方体三组相对的面上的4个顶点的和都相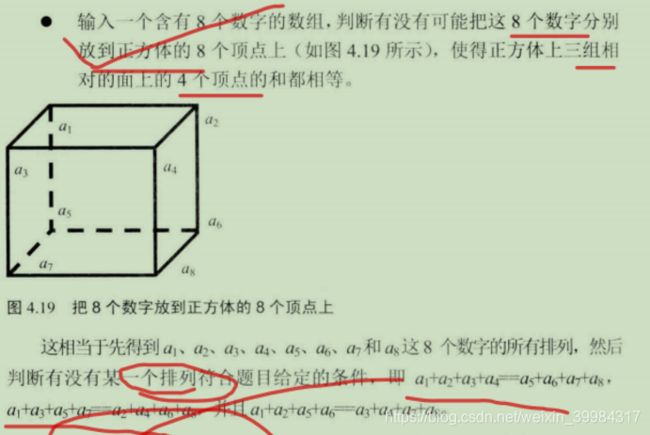

其实这道题跟字符串的排列是一样的，相当于先得到a1,a2,a3,a4,a5,a6,a7,a8这8个数字的所有排列，然后判断有没有某一个排列符合题目给定的条件，即
a1 + a2 + a3 + a4== a5 + a6 + a7 + a8
a1 + a3 + a5 + a7== a2 + a4 + a6 + a8
a1 + a2 + a5 + a6 == a3 + a4 + a7 + a8