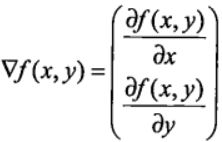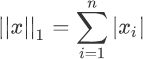Python机器学习算法入门教程（第二部分）

接着Python机器学习算法入门教程（第一部分），继续展开描述。

七、梯度下降求极值

在Python机器学习算法入门教程（第一部分）中的第六部分：线性回归：损失函数和假设函数一节，从数学的角度解释了假设函数和损失函数，我们最终的目的要得到一个最佳的“拟合”直线，因此就需要将损失函数的偏差值减到最小，我们把寻找极小值的过程称为“优化方法”，常用的优化方法有很多，比如共轭梯度法、梯度下降法、牛顿法和拟牛顿法。你可能对于上述方法感到陌生，甚至于害怕，其实大可不必，它们只不过应用了一些数学公式而已。

本节我们重点学习梯度下降法（Gradient Descent），在认识该方法之前，我们先复习一下高中时的数学知识。

1、导数

导数也叫导函数，或者微商，它是微积分中的重要基础概念，从物理学角度来看，导数是研究物体某一时刻的瞬时速度，比如你开车从家 8:00 出发到公司上班，9:00 到到达公司，这一个小时内的平均车速是 80km/h，而途中8:15:30这一时刻的速度，就被称为瞬时速度，此刻的速度可能是 100km/h，也可能是 20km/h。而从几何意义上来讲，你可以把它理解为该函数曲线在一点上的切线斜率。

导数有其严格的数学定义，它巧妙的利用了极限的思想，也就是无限趋近于 0 的思想。设函数 y=f(x) 在点 x0 的某个邻域内有定义，当自变量 x 在 x0 处有增量 Δx，(x0+Δx）也在该邻域内时，相应地函数取得增量 Δy=f(x0+Δx)-f(x0)；如果 Δy 与 Δx 之比当 Δx→0 时极限存在，则称函数 y=f(x) 在点 x0 处可导，并称这个极限为函数 y=f(x) 在点 x0 处的导数记做 ：

​

那么什么样的函数具有导数呢？是不是所有的函数都有导数？当然不是，而且函数也不一定在其所有点上都有导数。如果某函数在某一点导数存在，则称其在这一点可导，否则称为不可导。可导的函数一定连续；不连续的函数一定不可导。

导数的发明者是伟大的科学家牛顿与布莱尼茨，它是微积分的一个重要的支柱。在机器学习中，我们只需会用前辈科学家们留下来的知识就行了，比如熟悉常见的导函数公式，以下列举了常用的导数公式：

​

关于导数的的推断过程详细可参见百度百科。

2、偏导数

偏导数虽然和导数只有一字之差，但是却相差甚多，从它们的定义来看，偏导数是指对含有两个自变量的函数中的一个自变量求导，也就是说偏导数要求函数必须具备两个自变量。比如拿 z=f(x,y) 举例，如果只有自变量x变化，而自变量y固定（即看作常量），这时它就是x的一元函数，这函数对x的导数，就称为二元函数z对于x的偏导数，记做 fx(x,y) 。

有如下函数 z = x2 + 3xy + y2，分别求 z 对于 x 、y 的偏导数。如下所示：

fx(x,y) = 2x + 3y # 关于 x 的偏导数

fy(x,y) = 3x + 2y # 关于 y 的偏导数

当求 x 的偏导时就要把 y 当做常数项来对待，而当求 y 的偏导时就要把 x 当做常数项对待。关于偏导数还会涉及到高阶偏，如果感兴趣的话可以点击了解一下。

3、梯度下降

梯度下降是机器学习中常用的一种优化方法，主要用来解决求极小值的问题，某个函数在某点的梯度指向该函数取得最大值的方向，那么它的反反向自然就是取得最小值的方向。在解决线性回归和 Logistic（逻辑） 回归问题时，梯度下降方法有着广泛的应用。

梯度是微积分学的术语，它本质上是一个向量，表示函数在某一点处的方向导数上沿着特定的方向取得最大值，即函数在该点处沿着该方向变化最快，变化率最大。梯度下降法的计算过程就是沿梯度方向求解极小值，当然你也可以沿梯度上升的方向求解极大值。

那么如何能够更好的理解“梯度下降”呢？如果不考虑其他外在因素，其实你可以把它想象成“下山”的场景，如何从一个高山上以最快的时间走到山脚下呢？其实很简单，以你所在的当前位置为基准，寻找该位置最陡峭的地方，然后沿着此方向向下走，并且每走一段距离，都要寻找当前位置“最陡峭的地方”，反复采用上述方法，最终就能以最快的时间抵达山脚下。

在这个下山的过程中，“寻找所处位置最陡峭的地方，并沿此位置向下走”最为关键，如果把这个做法对应到函数中，就是找到“给定点的梯度”而梯度的方向就是函数值变化最快的方向。

​

图1：示意图

从上述描述中，你可能感觉到平淡无奇，其实每一个词语都蕴含着数学知识，比如“以当前所在位置为基准，找到最陡峭的地方”从数学角度来讲就是找到所在点的“切线”方向，也就是对这点“求导”，然后循着切线轨迹点反复使用此方法，就可以到达极小值点。

在第六部分：线性回归：损失函数和假设函数一节，我们讲解了线性回归的损失函数，而梯度下降作为一种优化方法，其目的是要使得损失值最小。因此“梯度下降”就需要控制损失函数的w和b参数来找到最小值。比如控制 w 就会得到如下方法：

w新=w旧 - 学习率 * 损失值

通过梯度下降计算极小值时，需要对损失函数的w求偏导求得，这个偏导也就是“梯度”，通过损失值来调节w，不断缩小损失值直到最小，这也正是梯度下降的得名来由。

“学习率”是一个由外部输入的参数，被称为“超参数”，可以形象地把它理解为下山时走的“步长”大小，想要 w 多调整一点，就把学习率调高一点。不过学习率也不是越高越好，过高的学习率可能导致调整幅度过大，导致无法求得真正的最小值。当损失函数取得极小值时，此时的参数值被称为“最优参数”。因此，在机器学习中最重要的一点就是寻找“最优参数”。

梯度下降是个大家族，它有很多成员，比如批量梯度下降（BGD）、随机梯度下降（SGD）、小批量梯度下降（MBGD），其中批量梯度下降是最常用的，相关内容后续会详细介绍。  

八、sklearn应用线性回归算法

Scikit-learn 简称 sklearn 是基于 Python 语言实现的机器学习算法库，它包含了常用的机器学习算法，比如回归、分类、聚类、支持向量机、随机森林等等。同时，它使用 NumPy 库进行高效的科学计算，比如线性代数、矩阵等等。

Scikit-learn 是 GitHub 上最受欢迎的机器学习库之一，其最新版本是 2020 年12 月发布的 scikit-learn 0.24.1。

提示：Scikit-learn 官方网站：

scikit-learn: machine learning in Python — scikit-learn 1.3.2 documentation

Scikit-learn 涵盖了常用的机器学习算法，而且还在不断的添加完善，对于本教程所涉及的机器学习算法它都做了良好的 API 封装，以供直接调用。你可以根据不同的模型进行针对性的选择。下面介绍 sklearn 中常用的算法库：

• ·linear_model：线性模型算法族库，包含了线性回归算法，以及 Logistic 回归算法，它们都是基于线性模型。
• .naiv_bayes：朴素贝叶斯模型算法库。
• .tree：决策树模型算法库。
• .svm：支持向量机模型算法库。
• .neural_network：神经网络模型算法库。
• .neightbors：最近邻算法模型库。

1、实现线性回归算法

下面我们是基于 sklearn 实现线性回归算法，大概可以分为三步，首先从 sklearn 库中导入线性模型中的线性回归算法，如下所示：

from sklearn import linear_model

其次训练线性回归模型。使用  fit() 喂入训练数据，如下所示：

model = linear_model.LinearRegression()
model.fit(x,y)

最后一步就是对训练好的模型进行预测。调用 predict() 预测输出结果， “x_”为输入测试数据，如下所示：

model.predict(x_)

你可能会感觉 so easy，其实没错，使用 sklearn 算法库实现线性回归就是这么简单，不过上述代码只是一个基本的框架，要想真正的把这台“机器”跑起来，我们就得给它喂入数据，因此准备数据集是必不可少的环节。数据集的整理也是一门专业的知识，会涉及到数据的收集、清洗，也就是预处理的过程，比如均值移除、归一化等操作，如果熟悉 Pandas 的话应该了解， 因此这里不做重点讲解。

（1）准备数据

下面我们手动生成一个数据集，如下所示：

# 使用numpy准备数据集
import numpy as np
# 准备自变量x
x = np.linspace(3,6,40)
#准备因变量y，这一个关于x的假设函数
y = 3 * x + 2

（2） 实现算法

#使用matplotlib绘制图像，使用numpy准备数据集
import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model

#准备自变量x，生成数据集，3到6的区间均分间隔30份数
x = np.linspace(3,6,40)

#准备因变量y，这一个关于x的假设函数
y = 3 * x + 2

#由于fit 需要传入二维矩阵数据，因此需要处理x，y的数据格式,将每个样本信息单独作为矩阵的一行
x=[[i] for i in x]
y=[[i] for i in y]
# 构建线性回归模型
model=linear_model.LinearRegression()
# 训练模型，"喂入"数据
model.fit(x,y)
# 准备测试数据 x_，这里准备了三组，如下：
x_=[[4],[5],[6]]
# 打印预测结果
y_=model.predict(x_)
print(y_)

#查看w和b的
print("w值为:",model.coef_)
print("b截距值为:",model.intercept_)

#数据集绘制,散点图，图像满足函假设函数图像
plt.scatter(x,y)
plt.show()

通过线性回归得到的线性函数图像，如下所示：

​

图1：线性回归函数图像

打印输出结果如下所示：

测试集输出结果：

[[14.]

[17.]

[20.]]

w值为: [[3.]]

b截距值为: [2.]

通过上述代码我们就实现“线性回归”的过程，但是在实际情况中，我们要面临的数据集要复杂的多，绝大多数情况不会这样理想，都会存在一些波动。在生成数据集的代码段内添加以下代码，如下所示：

#准备自变量x，生成数据集，3到6的区间均分间隔30份数
x = np.linspace(3,6，40)

#准备因变量y，这一个关于x的假设函数
y = 3 * x + 2

# 添加代码，扰乱点的分布
x = x + np.random.rand(40)

利用 NumPy 的 random. rand() 随机生成 0 - 1 之前的波动数值，从而改变数据点的分布情况，如下所示：

​

图2：修改后的散点分布

虽然做标签散乱分布，但是使用线性回归算法学习依然可以得到线性函数，此时 w 与 b 的输出结果如下所示：

w值为: [[2.68673744]]

b截距值为: [0.80154335]

绘制最佳拟合直线，程序代码如下：

#使用matplotlib绘制图像，使用numpy准备数据集
import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model

#准备自变量x，生成数据集
x = np.linspace(3,6.40)
#准备因变量y，这一个关于x的假设函数
y=3 * x + 2
#添加代码，扰乱点的分布
x = x + np.random.rand(40)
#由于fit 需要传入二维矩阵数据，因此需要处理x，y数据格式,将每个样本信息单独作为矩阵的一行
x=[[i] for i in x]
y=[[i] for i in y]

model=linear_model.LinearRegression()
model.fit(x,y)
#准备测试数据 x_，这里准备了三组，如下：
x_=[[4],[5],[6]]
# 打印预测结果
y_=model.predict(x_)
print(y_)

#查看w和b的
print("w值为:",model.coef_)
print("b截距值为:",model.intercept_)

#数据集绘制,散点图，图像满足函假设函数图像
plt.scatter(x,y)
#绘制最佳拟合直线
plt.plot(x_,y_,color="red",linewidth=3.0,linestyle="-")
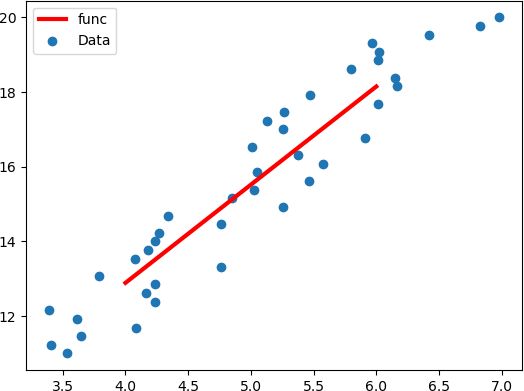
plt.legend(["func","Data"],loc=0)
plt.show()

函数图像如下所示：

​

图3：拟合直线绘制

2、线性回归步骤

通过上述代码了解了如何使用 Python  sklearn 实现线性回归，下面从总整体出发再次审视该算法：掌握线性回归算法的具体步骤。

线性回归适用于有监督学习的回归问题，首先在构建线性模型前，需要准备好待输入的数据集，数据集按照需要可划分为训练集和测试集，使用训练集中的向量 X 与向量 Y 进行模型的训练，其中向量 Y 表示对应 X 的结果数值(也就是“参考答案”)；而输出时需要使用测试集，输入测试 X 向量输出预测结果向量 Y。

其实线性回归主要解决了以下三个问题：

• 第一，为假设函数设定了参数 w，通过假设函数画出线性“拟合”直线。
• 第二，将预测值带入损失函数，计算出一个损失值。
• 第三，通过得到的损失值，利用梯度下降等优化方法，不断调整 w 参数，使得损失值取得最小值。我们把这个优化参数值的过程叫做“线性回归”的学习过程。

线性回归算法简单，且容易理解，但这并不影响它的广泛应用，比如经济金融领域实现股票的预测，以及著名的波士顿房价预测，这些都是线性回归的典型应有，因此我们要走出一个误区，不要感觉算法简单就不重要，机器学习虽然算法众多，但每一种算法都有其存在的理由，而掌握了线性回归就相当于拿到了算法世界的入场券。

九、Logistic回归算法（分类问题）

我们知道有监督学习分为“回归问题”和“分类问题”，前面我们已经认识了什么是“回归问题”，从本节开始我们将讲解“分类问题”的相关算法。在介绍具体的算法前，我们先聊聊到底什么是分类问题。

1、什么是分类问题？

其实想要理解“分类”问题非常的简单，我们不妨拿最简单的“垃圾分类处理”的过程来认识一下这个词。现在考虑以下场景：

小明拎着两个垃圾袋出门倒垃圾，等走到垃圾回收站的时候，小明发现摆放着两个垃圾桶，上面分别贴着“可回收”与“不可回收”。小明经过自己的判断后，把自己右手的垃圾放进了贴有“不可回收”的垃圾桶内，而左手的垃圾袋放进了“可回收”的垃圾桶内，最终完成了这次倒垃圾的过程。

其实上述“倒垃圾”的案例就说明了“分类问题”的过程。“可回收”与“不可回收”是两种预测分类，而小明是主观判断的个体，他通过自己日常接触的知识对“垃圾种类”做出判断，我们把这个程称作“模型训练”，只有通过“训练”才可以更加准确地判断“垃圾”的种类。小明进行了两次投放动作，每一次投放都要对“垃圾”种类做出预先判断，最终决定投放到哪个垃圾桶内。这就是根据模型训练的结果进行预测的整个过程。

下面对上述过程做简单总结：

• 类别标签：“可回收”与“不可回收”。
• 模型训练：以小明为主体，把他所接受的知识、经验做为模型训练的参照。
• 预测：投放垃圾的结果，预测分类是否正确。并输出预测结果。

分类问题是当前机器学习的研究热点，它被广泛应用到各个领域，比图像识别、垃圾邮件处理、预测天气、疾病诊断等等。“分类问题”的预测结果是离散的，它比线性回归要更加复杂，那么我们应该从何处着手处理“分类问题”呢，这就引出了本节要讲的 Logistic 回归分类算法。

2、Logistic回归算法（解决二分类问题）

多分类问题采用softmax函数

也许乍一看算法名字，你会认为它是用来解决“回归问题”的算法，但其实它是针对“分类问题”的算法。

Logistic 回归算法，又叫做逻辑回归算法，或者 LR 算法（Logistic Regression）。分类问题同样也可以基于“线性模型”构建。“线性模型”最大的特点就是“直来直去”不会打弯，而我们知道，分类问题的预测结果是“离散的”，即对输出数据的类别做判断。比如将类别预设条件分为“0”类和“1”类（或者“是”或者“否”）那么图像只会在 “0”和“1”之间上下起伏，如下图所示：

​

图1：离散型数据

此时你就可能会有很多疑问，线性回归函数不可能“拟合”上述图像。没错，所以接下来我们要学习另一个线性函数 Logistic 函数。

注意：在机器学习中，Logistic 函数通常用来解决二元分类问题，也就是涉及两个预设类别的问题，而当类别数量超过两个时就需要使用 Softmax 函数来解决。

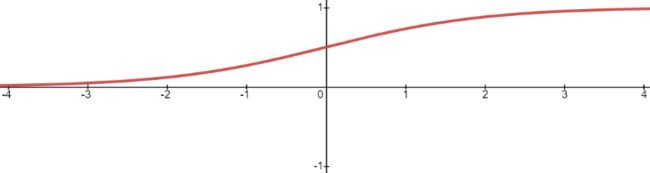
19 世纪统计学家皮埃尔·弗朗索瓦·韦吕勒发明了 Logistic 函数，该函数的叫法有很多，比如在神经网络算法中被称为 Sigmoid 函数，也有人称它为 Logistic 曲线。其函数图像如下所示：

​

图2：Logistic曲线函数

该函数图像的数学表达式如下：

​

e 称为自然常数，也就是一个固定值的“常量”， 是以 e 为底、z 为变量的指数函数，还可以写为，在编写程序代码时，通常将其写为 exp(-x)。至于这个表达式是如何推断出来的，我们没有必要深究，学会站在“巨人”的肩膀上学习也是一种难得的品质。

Logistic 函数也称为 S 型生长曲线，取值范围为 (0,1)，它可以将一个实数映射到 (0,1) 的区间，非常适合做二元分类。当 z=0 时，该函数的取值为 0.5，随着 z 的增大，对应的函数值将逼近于 1；而随着 z 的减小，其函数值将逼近于 0。

对于 Logistic 函数而言，坐标轴 0 是一个有着特殊意义坐标，越靠近 0 和越远离 0 会出现两种截然不同的情况：任何大于 0.5 的数据都会被划分到 “1”类中；而小于 0.5 会被归如到 “0”类。因此你可以把 Logistic 看做解决二分类问题的分类器。如果想要 Logistic 分类器预测准确，那么 x 的取值距离 0 越远越好，这样结果值才能无限逼近于 0 或者 1。

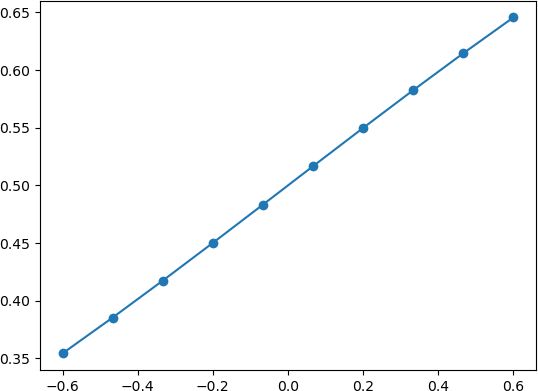
下面通过极限的思想进一步对上述函数展开研究：我们可以考虑两种情况：当 x 轴坐标取值缩小时就会出现以下图像：

​

图3：Logistic函数

由此可见 Logistic 回归算法属于“线性”模型。而当 x 逐渐放大时则会出现以下情况：

​

图4：Logistic函数

由上图可知，当 x 增大到一定程度时，Logistic 函数图像变成了“台阶”式图像，由此可知，该函数能够很好的“拟合”二分类问题函数图像。在数学上，我们把具有如图 4 所示，这种“阶梯式”图像的函数称为“阶跃函数”。

本节我们重点讲解了什么是分类问题，并且还花费了较大的篇幅讲解了 Logistic 函数，该函数解决二元分类问题的关键所在。Logistic 函数至关重要后续还会做相应介绍。

十、数学解析Logistic回归算法

在第九节，我们学习了 Logistic 回归算法，并且重点认识了 Logistic 函数。我们知道分类问题的预测结果是离散型数据，那么我们在程序中要如何表述这些数据呢，再者我们要如何从数学角度理解 Logistic 算法，比如它的损失函数、优化方法等。

1、分类数据表示形式

（1） 向量形式

在机器学习中，向量形式是应用最多的形式，使用向量中的元素按顺序代表“类别”。现在有以下三个类别分别是 a/b/c，此时就可以使用 [1,2,3] 来分别代表上述三类，预测结果为哪一类，向量中的元素就对应哪个元素，比如当预测结果为 c 类的时候，则输出以下数据：

[0,0,3]

（2） 数字形式

数字形式是一种最简单的分类方式，我们可以用 0 代表“负类”（即 x < 0时的取值），而用“1”代表正类（即 x>0 时的取值），那么当预测结果输出“1”就代表正类，而预测结果输出“0”代表“负类”。当然这里选择的数字只是形式，你可以选择任意其他数字，不过按照约定俗成，我们一般采用 “1”代表正类，而 “-1”或者“0”代表“负类”。 如果用代码的表示数字形式的中心思想，如下所示：

#以 0 为节将其分开
if (logistic函数输出的是连续值>0):
    return 1

else:
    return 0

（3） 概率形式

在有些实际场景中，我们无法准确的判断某个“样本”属于哪个类别，此时我们就可以使用“概率”的形式来判断“样本”属于哪个类别的几率大，比如对某个“样本”有如下预测结果：

[0.8,0.1,0.1]

从上述输出结果不难看出，该样本属于 a 类的概率最大，因此我们可以认定该样本从属于 a 类。

2、Logistic函数数学解析

（1） 假设函数

经过上一节的学习得知 Logistic 函数能够很好的拟合“离散数据”，因此可以把它看做“假设函数”，但是还需要稍稍的改变一下形式，如下所示：

​

上述公式和 Logistic 函数基本一致，只不过我们它换成了关于x的表达式，并将幂指数x换成了 “线性函数”表达式。H(x) 的函数图像呈现 S 形分布，从而能够预测出离散的输出结果。

（2） 损失函数

LogIstic 回归算法的损失函数有点复杂，也许你会感动莫名其妙，损失函数的表达式如下：

​

想要理解损失函数，我们需要继续分析假设函数。我们知道假设函数的值域是从 (0,1) 之间的数值，而这个数据区间恰好与概率值区间不谋而合。如果我们把预测结果看做概率，则可以得到另外一种写法的损失函数：

​

上述函数是根据概率设计出来的，它由 ​ 和 ​两部分组成，由于 y 值的取值只会是 0 或者 1，所以每次只有一个部分输出值，因此可以达到分类的目的。

我们知道 y 输出值概率值只能为 0 或者 1，因此上述函数只会有一部分输出数值。即当 y=1 时候，1-y 就等于 0，因此上述表达式的第二部分，也就是​ 的值为 1，相乘后并不会对函数值产生影响。当 y = 0 时，同理。

综上所述：当 y=1 时，如果预测正确，预测值则无限接近 1，也即 ​的值为 1，损失值则为 -1；如果预测错误，​的值为 0，损失值也为 0。预测错误的损失值确实比预测正确的损失值大（0 > -1），满足要求。

虽然上述函数能够表达预测值和实际值之间的偏差，但它有一个缺点就是不能使用梯度下降等优化方法。因此，在机器学习中要通过取对数的方法来解决此问题，这样就得到了最开始的损失函数。如下所示：

​

（3） 优化方法

如果将 Logistic 函数的输出记做 z 可得如下公式：

z = w0x0+w1x1<+....+wnxn

采用向量的形式可以写为：

它表示将这两个数值向量对应元素相乘然后全部加起来即得到 z 值。其中的 x 是分类器的输入数据，向量 w （最佳参数）会使得分类器尽可能的精确。为了寻找该最佳参数就需要用到优化方法，下面我们简单介绍梯度上升优化方法。

3、梯度上升优化方法

梯度上升与梯度下降同属于优化方法，它们两者有着异曲同工之妙，梯度下降求的是“最小值”，而梯度上升求的是“最大值”。梯度上升基于的思想是：要找到某函数的最大值，最好的方式是沿着该函数的梯度方向寻找，如果把梯度记为▽，那么关于 f(x,y) 有以下表达式：

​

上述公式是其实并不难理解，该函数分别对 x 与 y 求的偏导数，其中关于 x 的偏导数表示沿着 x 的方向移动，而关于 y 的偏导数一个表示沿 y 的方向移。其中，函数f(x,y) 必须要在待计算的点上可导。在梯度上升的过程中，梯度总是指向函数值增长最快的方向，我们可以把每移动一次的“步长”记为α 。用向量来表示的话，其公式如下：

​

在梯度上升的过程中，上述公式将一直被迭代执行，直至达到某个停止条件为止，比如达到某个指定的值或者某个被允许的误差范围之内。

十一、sklearn应用Logistic回归算法

在 Scikit-Learn 机器学习库中，有关线性模型的算法族都在linear_model模块下，不同的算法又会分化为很多类，但它们都是经过几种基本算法调整和组合而成，因此基本上都是大同小异，换汤不换药，下面介绍经常用到回归类算法，其中就包含了 Logistic 回归算法。在这之前我们需要先熟悉几个概念，比如“正则化”。

1、什么是范数？

范数又称为“正则项”，它是机器学习中会经常遇到的术语，它表示了一种运算方式，“范数”的种类有很多，不过常见的范数主要分为两种：L1 和 L2。下面我们来分别认识一下它们。

（1） L1范数

L1 范数非常容易理解，它表示向量中每个元素绝对值的和，根据定义，L1 范数的计算分两步，首先逐个求得元素的绝对值，然后相加求和即可。下面给出了 L1 范数正则化定义的数学表达式，如下所示：

​

注意：此时两个绝度值符号，是符合范数规定的，两个绝对值符号表示范数。

（2） L2范数

L2 范数出现的频率更高，表示向量中每个元素的平方和的平方根。根据定义，L2 范数的计算分三步，首先逐个求得元素的平方，然后相加求和，最后求和的平方根。L2范数正则化定义的数学表达式如下：

​

2、回归类算法

除了“线性回归算法” 也就是“最小二乘法”之外，还有以下常用算法：

（1） Ridge类

Ridge 回归算法，又称“岭回归算法”主要用于预测回归问题，是在线性回归的基础上添加了 L2 正则项，使得权重 w 的分布更加均匀，其损失函数如下：

​

损失函数的左侧与线性回归算法的损失函数一致。只是在最后添加右侧的 L2 正则项，其中 a  只是一个常数，需要根据经验设置。

注意，线性回归函数的 1/n 在优化过程的运算中不会影响结果，它只是一个常量而已，而常量的导数是 0。

（2） Lasso类

Lasso 回归算法：我们知道，常用的正则项有 L1 和 L2，而使用了 L1 正则项的线性回归是 Lasso 回归算法，它可以预测回归问题，其损失函数的表达式如下（求最小损失值）： 

​

上述表达式的左侧与 Ridge 回归算法的损失函数基本一致，只是将右侧的 L2 范数替换成了 L1 范数，而且左侧式子相比线性回归表达式而言，多了一个1/2，但实际的优化过程中，它并不会对权重 w 产生影响。

3、实现Logistic回归

下面使用 skleran 库实现 Logistic 回归算法，首先导入一下模块：

from sklearn.linear_model import LogisticRegression

sklearn 库中自带了许多种类的内建数据集，比如波士顿房价数据集，手写数字识别数据集，鸢尾花数据集，糖尿病数据集等，这些数据集对我们学习机器学习算法提供了很好的帮助，节省了我们收集、整理数据集的时间。下面我们以鸢尾花数据集对 Logistic 回归算法进行简单的应用。

#logistic算法
#从 scikit-learn库导入线性模型中的logistic回归算法
from sklearn.linear_model import LogisticRegression
#导入sklearn 中的自带数据集 鸢尾花数据集
from sklearn.datasets import load_iris
# skleran 提供的分割数据集的方法
from sklearn.model_selection import train_test_split

#载入鸢尾花数据集
iris_dataset=load_iris()

# data 数组的每一行对应一朵花，列代表每朵花的四个测量数据，分别是：花瓣的长度，宽度，花萼的长度、宽度
print("data数组类型: {}".format(type(iris_dataset['data'])))
# 前五朵花的数据
print("前五朵花数据:\n{}".format(iris_dataset['data'][:5]))

#分割数据集训练集，测试集
X_train,X_test,Y_train,Y_test=train_test_split(iris_dataset['data'],iris_dataset['target'],random_state=0)

#训练模型
#设置最大迭代次数为3000，默认为1000.不更改会出现警告提示
log_reg = LogisticRegression(max_iter=3000)
#给模型喂入数据
clm=log_reg.fit(X_train,Y_train)

#使用模型对测试集分类预测,并打印分类结果
print(clm.predict(X_test))
#最后使用性能评估器，测试模型优良，用测试集对模型进行评分
print(clm.score(X_test,Y_test))

输出结果如下：

data 数组类型:

前五朵花数据:

[[5.1 3.5 1.4 0.2]

[4.9 3. 1.4 0.2]

[4.7 3.2 1.3 0.2]

[4.6 3.1 1.5 0.2]

[5. 3.6 1.4 0.2]]

测试集划分结果：

[2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0 2 1 0 2 2 1 0 2]

模型评分：

0.9736842105263158

scikit-learn 中的 train_test_split 函数可以打乱数据集，并对其进行拆分。该函数默认将 75% 的行数据及对应标签作为训练集，另外 25% 数据作为测试集。

注意：75% 和 25% 这两个数值可以根据实际的情况做相应的调整。

最后，我们对 Logistic 算法做一下简单总结：

首先 Logistic 算法适用于分类问题，该算法在处理二分类问题上表现优越，但在多分类（二个以上）问题上容易出现欠拟合。

Logistic 算法除了适用于回归分类问题，还可以作为神经网络算法的激活函数（即 Sigmoid 函数）。

机器学习中有许多的算法，我们不能评价一个算法的优劣性，因为算法只有合适与不合适，每个算法都有其适用的场景。因此，我们不能仅依据模型评分来评价模型的好与坏。这就好比从每个班级中选出数学非常优秀的学生去参加数学竞赛一样，如果竞赛的第一名只得了 60 分，而其余学生都不及格，那你会说他们都是是个差生吗，因此，在后续学习机器学习算法的过程中要牢记这一点。

十二、KNN最邻近分类算法

未知样本用与它最近邻的k个已知样本来表示

本节继续探机器学习分类算法——K 最近邻分类算法，简称 KNN（K-Nearest-Neighbor），它是有监督学习分类算法的一种。所谓 K 近邻，就是 K 个最近的邻居。比如对一个样本数据进行分类，我们可以用与它最邻近的 K 个样本来表示它，这与俗语“近朱者赤，近墨者黑”是一个道理。

在学习 KNN 算法的过程中，你需要牢记两个关键词，一个是“少数服从多数”，另一个是“距离”，它们是实现 KNN 算法的核心知识。

1、KNN算法原理

为了判断未知样本的类别，以所有已知类别的样本作为参照来计算未知样本与所有已知样本的距离，然后从中选取与未知样本距离最近的 K 个已知样本，并根据少数服从多数的投票法则（majority-voting），将未知样本与 K 个最邻近样本中所属类别占比较多的归为一类。这就是 KNN 算法基本原理。

在 scikit-learn 中 KNN 算法的 K 值是通过 n_neighbors 参数来调节的，默认值是 5。

KNN 算法原理：如果一个样本在特征空间中存在 K 个与其相邻的的样本，其中某一类别的样本数目较多，则待预测样本就属于这一类，并具有这个类别相关特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

KNN 算法简单易于理解，无须估计参数，与训练模型，适合于解决多分类问题。但它的不足是，当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有很能导致当输入一个新样本时，该样本的 K 个邻居中大容量类的样本占多数，而此时只依照数量的多少去预测未知样本的类型，就会可能增加预测错误概率。此时，我们就可以采用对样本取“权值”的方法来改进。

2、KNN算法流程

下面对 KNN 算法的流程做简单介绍。KNN 分类算法主要包括以下 4 个步骤：

• 准备数据，对数据进行预处理 。
• 计算测试样本点（也就是待分类点）到其他每个样本点的距离（选定度量距离的方法）。
• 对每个距离进行排序，然后选择出距离最小的 K 个点。
• 对 K 个点所属的类别进行比较，按照少数服从多数的原则（多数表决思想），将测试样本点归入到 K 个点中占比最高的一类中。

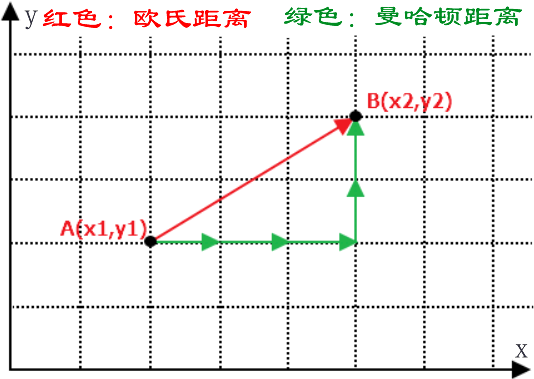
注意：在机器学习中有多种不同的距离公式，下面以计算二维空间 A(x1,y1)，B(x2,y2) 两点间的距离为例进行说明，下图展示了如何计算欧式距离和曼哈顿街区距离。（PS:要理会名字，名字都是纸老虎）如下图所示：

​在前面提到过欧氏距离，它表示两点之间最短的距离，其计算公式如下：

​
曼哈顿街区距离计算公式如下：

​
那么你会考虑它们两者的区别是什么呢？其实很容易理解，我们知道两点之前线段最短，A 和 B 之间的最短距离就是“欧式距离”，但是在实际情况中，由于受到实际环境因素的影响，我们有时无法按照既定的最短距离行进，比如你在一个楼宇众多的小区内，你想从 A 栋达到 B 栋，但是中间隔着其他楼房，因此你必须按照街道路线行进（图中红线），这种距离就被称作“曼哈顿街区距离”。

注意：除上述距离外，还有汉明距离、余弦距离、切比雪夫距离、马氏距离等。在 KNN 算法中较为常用的距离公式是“欧氏距离”。

3、KNN预测分类

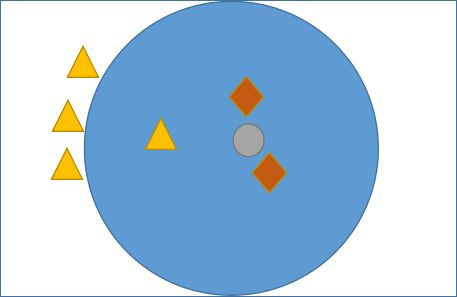
通过上述介绍我们理解了 KNN 算法的基本工作流程，它主要利用“多数表决思想”与“距离”来达到分类的目的，那么我们应该如何确定 K 值呢？因为不同的 K 值会影响分类结果，如下所示：

​图1：KNN算法分类核心

如图 1 所示，有三角形和菱形两个类别，而“灰色圆”是一个未知类别，现在通过 KNN 算法判断“灰色圆”属于哪一类。如果当 K 的取值为 3 时，按照前面讲述的知识，距离最近且少数服从多数，那“灰色圆”属于菱形类，而当 K= 6 时，按照上述规则继续判断，则“灰色圆”属于三角形类。

KNN 分类算法适用于多分类问题、OCR光学模式识别、文本分类等领域。

下一部分将在Python机器学习算法入门教程（第三部分）展开描述。