【算法】【排序】10大常见排序算法解析(附大量图片演示+完整测试代码)
首先聊一聊什么是排序?
所谓排序
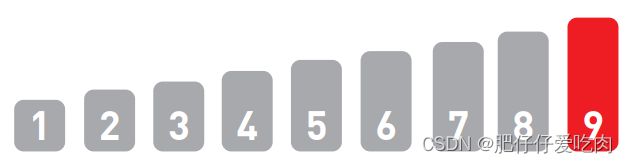
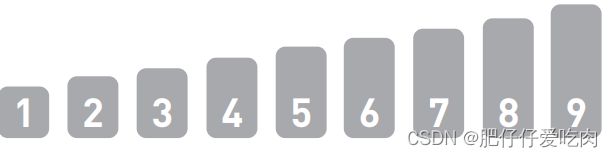
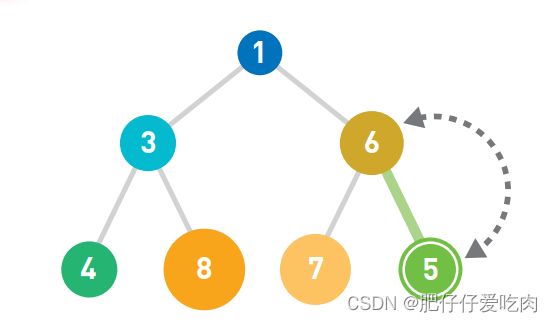
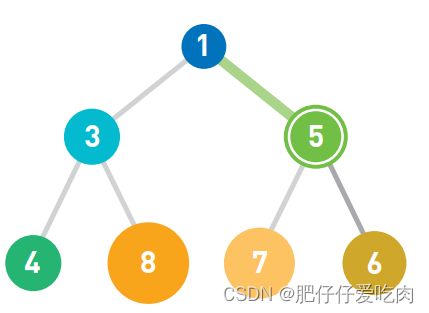
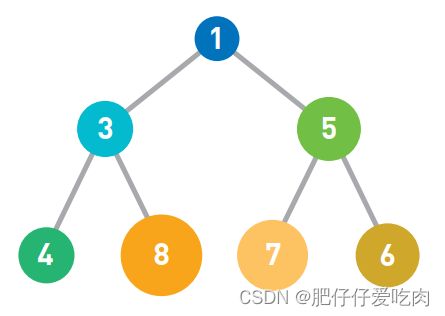
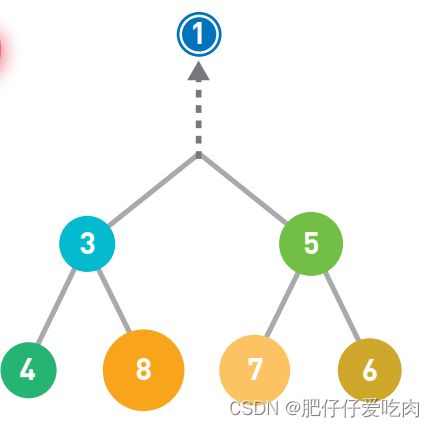
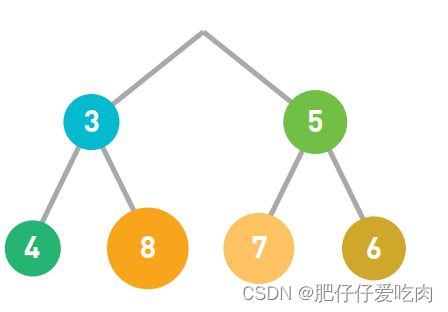
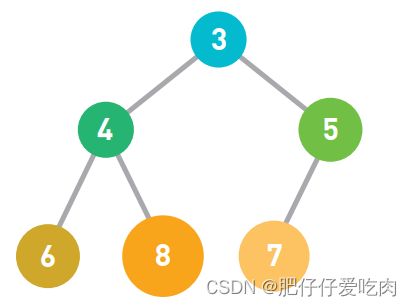
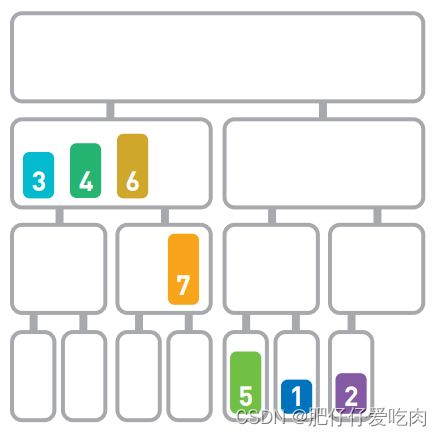
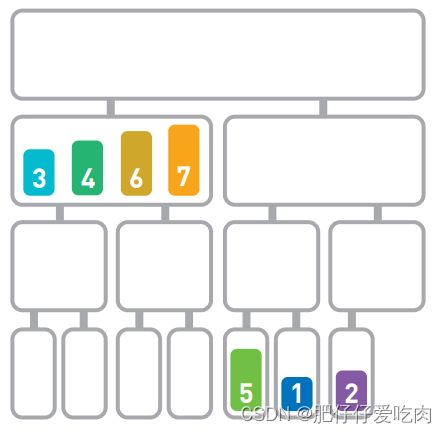
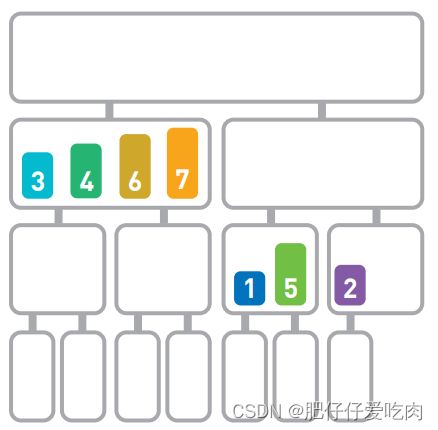
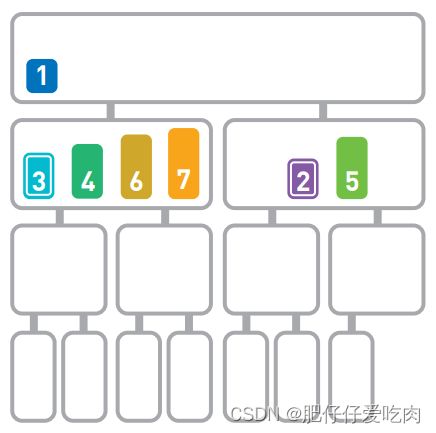
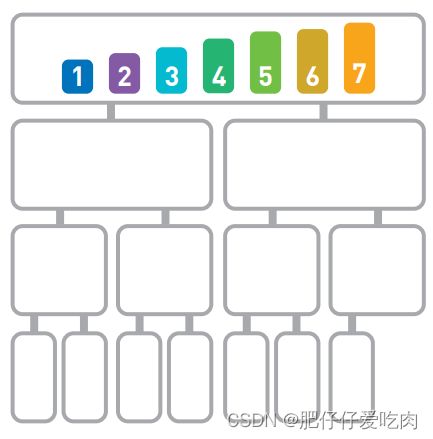
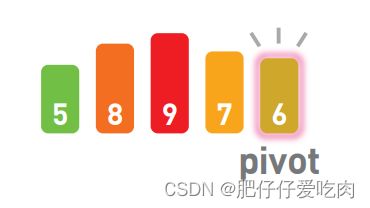
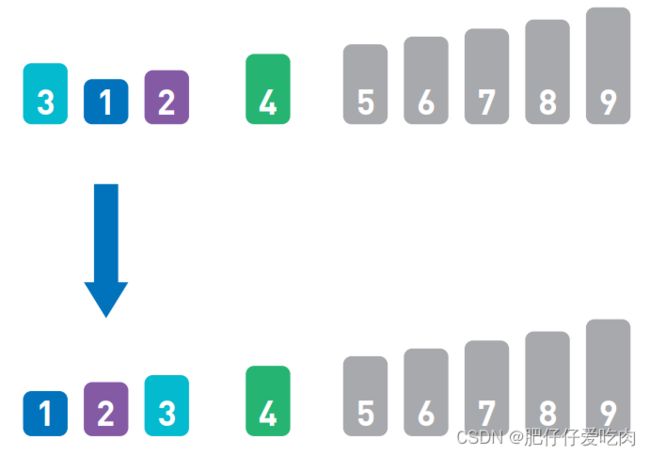
排序就是将输入的数字按照从小到大的顺序进行排列。这里我们用柱形来表示数字,数字越大,柱形就越高。
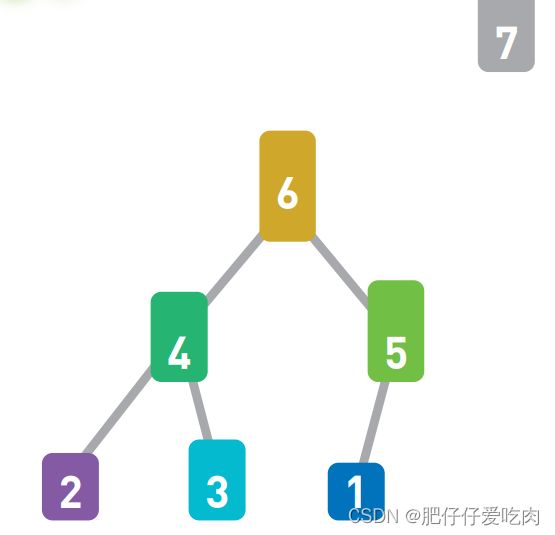
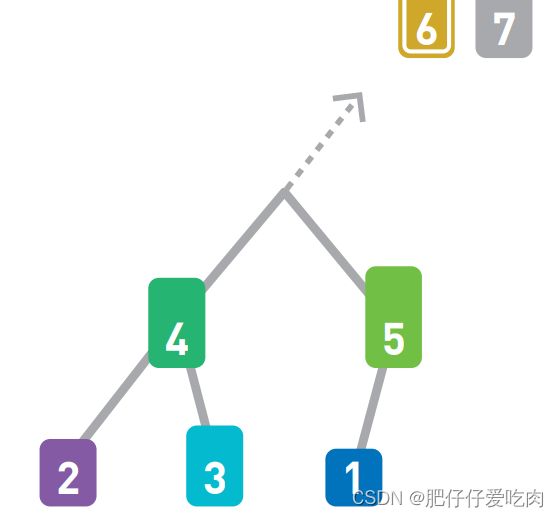
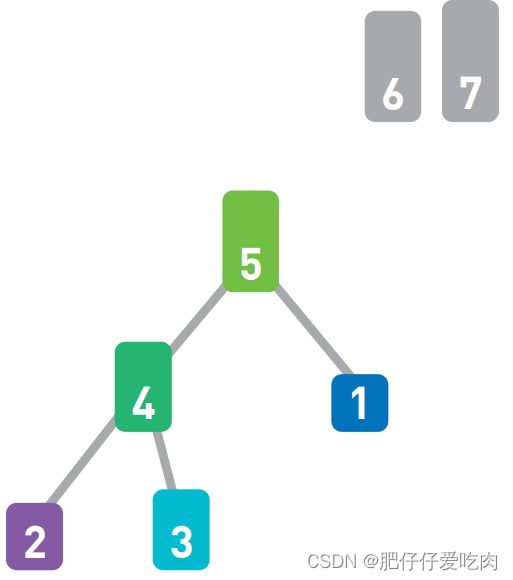
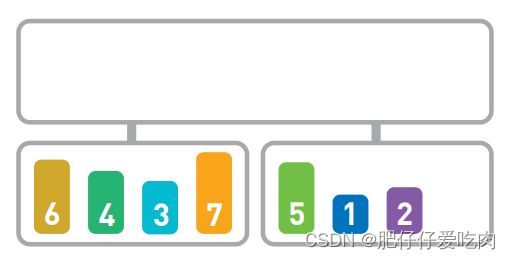
假设现在有如上图所示的输入数据,那么我们的目标就是将它们像下图一样,按从小到大的顺序从左边开始依次排列。
如果只有10 个数字,手动排序也能轻松完成,但如果有10000个数据,排序就不那么容易 了。这时,使用高效率的排序算法便是解决问题的关键
各种各样的排序算法:
| 排序算法 | 时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 | 排序方式 | 稳定性 | 排序类型 |
| 1.冒泡排序 | O(n^2) | O(n) | O(n^2) | O(1) | In-place | 稳定 | 比较 |
| 2.选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | In-place | 不稳定 | 比较 |
| 3.插入排序 | O(n^2) | O(n) | O(n^2) | O(1) | In-place | 稳定 | 比较 |
| 4.堆排序 | O(n logn) | O(n logn) | O(n logn) | O(1) | In-place | 不稳定 | 比较 |
| 5.归并排序 | O(n logn) | O(n logn) | O(n logn) | O(n) | Out-place | 稳定 | 比较 |
| 6.快速排序 | O(n logn) | O(n logn) | O(n^2) | O(logn) | In-place | 不稳定 | 比较 |
| 7.希尔排序 | O(n^1.5) | O(n logn) | O(n^2) | O(1) | In-place | 不稳定 | 比较 |
| 8.计数排序 | O(n+k) | O(n+k) | O(n+k) | O(k) | Out-place | 稳定 | 非比较 |
| 9.桶排序 | O(n+k) | O(n+k) | O(n^2) | O(n+k) | Out-place | 稳定 | 非比较 |
| 10.基数排序 | O(n*k) | O(n*k) | O(n*k) | O(n+k) | Out-place | 稳定 | 非比较 |
名词解释:
时间复杂度:一个算法执行所耗费的时间。
空间复杂度:运行完一个程序所需内存的大小。
内排序:所有排序操作都在内存中完成。
外排序:由于数据太大,因此把数据放在磁盘中,而排序通过磁盘和内存的数据传输才能进行。
稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
不稳定:如果a原本在b的前面,而a=b,排序之后a可能会出现在b的后面。
目录
首先聊一聊什么是排序?
所谓排序
各种各样的排序算法:
名词解释:
十种排序算法
1.冒泡排序
看图理解:
核心代码1:
核心代码2:
测试代码:
2.选择排序
看图理解:
核心代码:
测试代码:
3.插入排序
看图理解:
核心代码:
测试代码:
4.堆排序
堆的了解:
看图理解:
核心代码:
测试代码:
5.归并排序
看图理解:
核心代码:
测试代码:
6.快速排序
看图理解:
核心代码:
测试代码:
7.希尔排序
看图理解:
核心代码:
测试代码:
8.计数排序
看图理解:
完整代码:
9.桶排序
看图理解:
完整代码:
10.基数排序
看图理解:
完整代码:
参考书籍:
前言:本章篇幅较长,大家可以点击目录快速找到自己需要了解的排序算法。
本章每种排序算法主要由“看图理解”、“核心代码”和“测试代码”三部分组成,看图理解可以快速了解算法原理,核心代码是排序算法实现(干货可多看看),加上测试代码可以运行测试对应的排序算法。
推荐:另外推荐大家读一下《我的第一本算法书》,书中通过大量图示的方式描述了多种排序算法的实现过程。《挑战程序设计竞赛2》,该书中满满都是干货,本章中大量代码实现都有参考该书籍。
十种排序算法
1.冒泡排序
冒泡排序就是重复“从序列右边开始比较相邻两个数字的大小,再根据结果交换两个数字的位置”这一操作的算法。在这个过程中,数字会像泡泡一样,慢慢从右往左“浮”到序列的 顶端,所以这个算法才被称为“冒泡排序”。
看图理解:
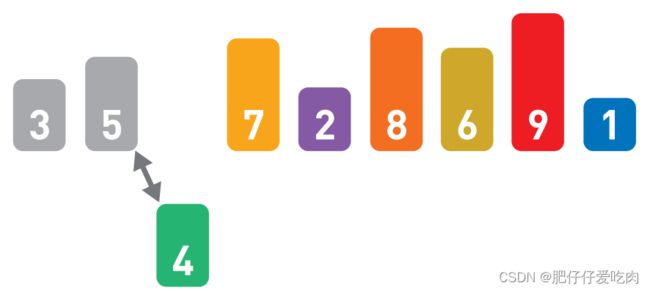
1.1在序列的最右边放置一个天平,比较天平两边的数字。如果右边的数字较小,就交换这两个数字的位置。
1.2由于6<7,所以交换这两个数字。
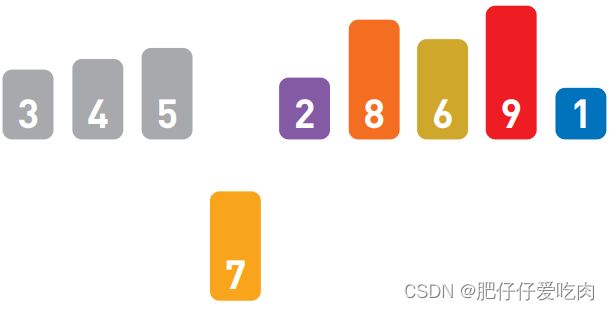
1.3完成后,天平往左移动一个位置,比较两个数 字的大小。此处4<6,所以无须交换。
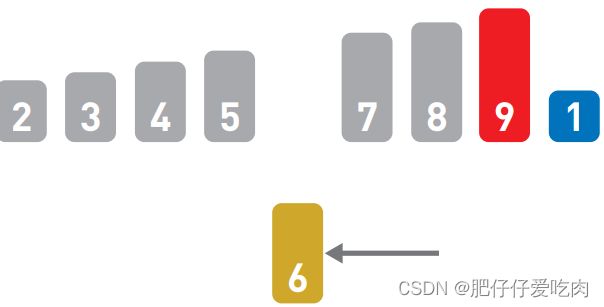
1.4继续将天平往左移动一个位置并比较数字。重复同样的操作直到天平到达序列最左边为止。
1.5不断对数字进行交换,天平最终到达了最左边。通过这一系列操作,序列中最小的数字就会移动到最左边
1.6最左边的数字已经归位。
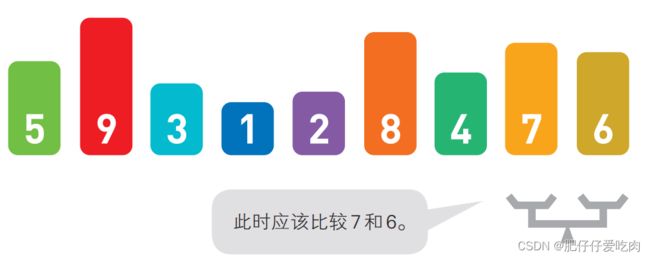
1.7将天平移回最右边,然后重复之前的操作,直到天平到达左边第2个位置为止。
1.8当天平到达左边第2个位置时,序列中第2小的数字也就到达了指定位置。
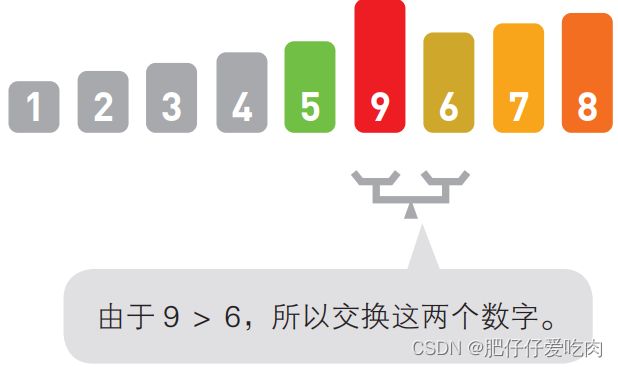
1.9将天平再次移回最右边,重复同样的操作直到所有数字都归位为止。
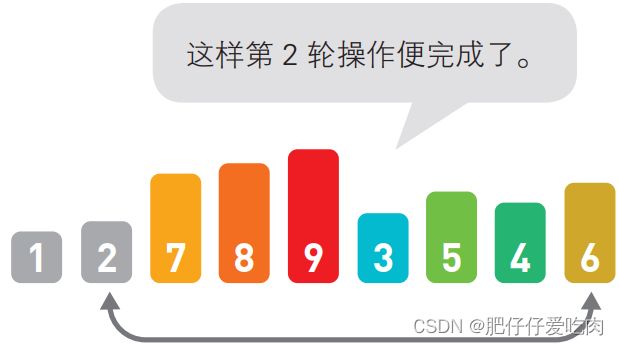
1.10排序中……
1.11排序中……
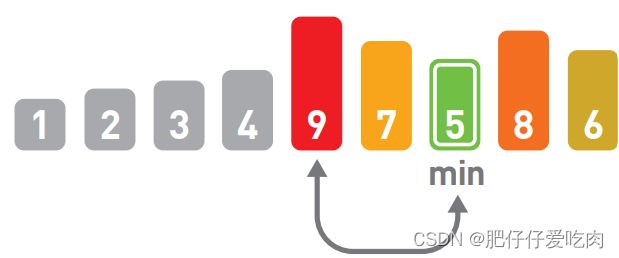
1.12排序完成。
核心代码1:
/* 冒泡排序--普通版 */
void BubbleSort1(int arr[], int len)
{
int i, j;
/*循环遍历*/
for (i = 0; i < len; i++)
{
for (j = len - 1; j >= i + 1; j--)
{
if (arr[j] < arr[j - 1])
{
/* 交换数据 */
int temp=arr[j];
arr[j]=arr[j-1];
arr[j-1]=temp;
/* 调用swap函数交换数据,效率会更高 */
//swap(arr[j], arr[j - 1]);
}
}
}
}核心代码2:
/* 冒泡排序--升级版 */
void BubbleSort2(int arr[],int len)
{
int i, j;
/* flag用来作为标记 */
bool flag = true;
/* 若flag为true说明有过数据交换,若没有数据交换,falg为false则数据已经全部是顺序的了 */
for (i = 0; flag; i++)
{
/* 初始为false */
flag = false;
for (j = len - 1; j >= i+1; j--)
{
if (arr[j] < arr[j - 1])
{
/* 交换数据 */
int temp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = temp;
/* 调用swap函数交换数据,效率会更高 */
//swap(arr[j], arr[j - 1]);
/* 如果有数据交换,则flag为true */
flag = true;
}
}
}
}测试代码:
#include
#include
using namespace std;
int main()
{
int arr[100];
int len;
cout << "请输入数组个数:";
cin >> len;
cout << "请依次输入"<> arr[i];
}
#if 0 //为0则选用BubbleSort2(arr, len);为1则选用BubbleSort1(arr, len);
BubbleSort1(arr, len);
#else
BubbleSort2(arr, len);
#endif
/*打印数组*/
for (int i = 0; i < len; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
} 2.选择排序
选择排序就是重复“从待排序的数据中寻找最小值,将其与序列最左边的数字进行交换” 这一操作的算法。在序列中寻找最小值时使用的是线性查找。
看图理解:
2.1对数字1~9进行排序。
2.2使用线性查找在数据中寻找最小值,于是我们找到了最小值 1。
2.3将最小值 1 与序列最左边的 6 进行交换,最小值 1 归位。不过,如果最小值已经在最左端,就不需要任何操作。
2.4在余下的数据中继续寻找最小值。这次我们找到了最小值2。
2.5将数字 2 与左边第 2 个数字 6 进行交换,最小值 2归位。
2.6重复同样的操作直到所有数字都归位为止。
2.7排序完成。
核心代码:
/* 选择排序 */
void selectionSort(int arr[], int len) {
int i, j;
int minj;
for (i = 0; i < len - 1; i++) {
/*minj标记最小数据的下标*/
minj = i;
for (j = i; j < len; j++) {
if (arr[j] < arr[minj]) {
minj = j;
}
}
/*每循环一次找到一个最小值,当最小值下标是其他位置时,进行交换*/
if (i != minj) {
int temp = arr[i];
arr[i] = arr[minj];
arr[minj] = temp;
/* 调用swap函数交换数据,效率会更高 */
//swap(arr[i], arr[minj]);
}
}
}测试代码:
#include
#include
using namespace std;
int main()
{
int arr[100];
int len;
cout << "请输入数组个数:";
cin >> len;
cout << "请依次输入" << len << "个数组元素,以空格分开,回车结束" << endl;
for (int i = 0; i < len; i++) {
cin >> arr[i];
}
selectionSort(arr, len);
/*打印数组*/
for (int i = 0; i < len; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
} 3.插入排序
插入排序是一种从序列左端开始依次对数据进行排序的算法。在排序过程中,左侧的数据陆续归位,而右侧留下的就是还未被排序的数据。插入排序的思路就是从右侧的未排序区域内取出一个数据,然后将它插入到已排序区域内合适的位置上。
看图理解:
3.1此处同样对数字1~9进行排序。
3.2首先,我们假设最左边的数字5已经完成排序,所以此时只有5是已归位的数字。
3.3接下来,从待排数字(未排序区域)中取出最左边的数字 3,将它与左边已归位的数字进行比较。若左 边的数字更大,就交换这两个数字。重复该操作,直到左边已归位的数字比取出的数字更小,或者取 出的数字已经被移到整个序列的最左边为止。
3.4由于5>3,所以交换这两个数字。
3.5对数字3的操作到此结束。此时3和5已归位,还剩下右边7个数字尚未排序。
3.6接下来是第3轮。和前面一样,取出未排序区域中最左边的数字4,将它与左边的数字5进行比较。
3.7由于 5 > 4,所以交换这两个数字。交换后再把 4 和左边的 3 进行比较,发现 3 < 4,因为出现了比自己 小的数字,所以操作结束。
3.8于是4也归位了。此时3、4、5都已归位,已 排序区域也得到了扩大。
3.9遇到左边的数字都比自己小的情况时……
3.10不需要任何操作即可完成排序。
3.11重复上述操作,直到所有数字都归位。
3.12对所有数字的操作都结束时,排序也就完成了。
核心代码:
/* 插入排序 */
void insertionSort(int arr[], int len) {
int i, j;
int v;
/* 循环从第二个元素(arr[1])开始,第一个元素(arr[0])本身看作是有序的 */
for (i = 1; i < len; i++) {
/* v保存的是最新待排序的数据 */
v = arr[i];
/* j为已排序区域最右端数据下标 */
j = i - 1;
/* 循环比较,直到找到v待插入的位置 */
while (arr[j] > v) {
/* 待插入v数据值较小,较大数据往后移动一位 */
arr[j + 1] = arr[j];
j--;
}
/* 此时的arr[j]>v不成立,即v下标位置为j+1 */
arr[j + 1] = v;
}
}测试代码:
#include
#include
using namespace std;
int main()
{
int arr[100];
int len;
cout << "请输入数组个数:";
cin >> len;
cout << "请依次输入" << len << "个数组元素,以空格分开,回车结束" << endl;
for (int i = 0; i < len; i++) {
cin >> arr[i];
}
insertionSort(arr, len);
/*打印数组*/
for (int i = 0; i < len; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
} 4.堆排序
堆排序的特点是利用了数据结构中的堆。
注:下面先了解堆实现过程,若已了解可略过。
堆的了解:
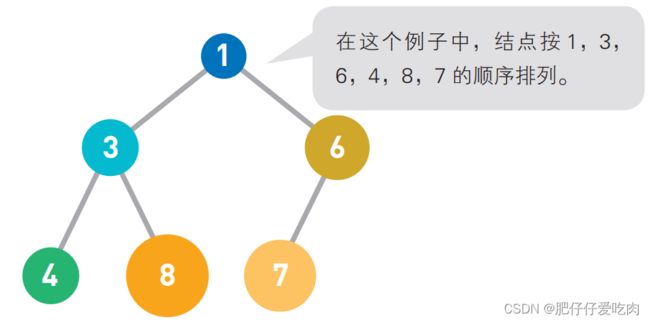
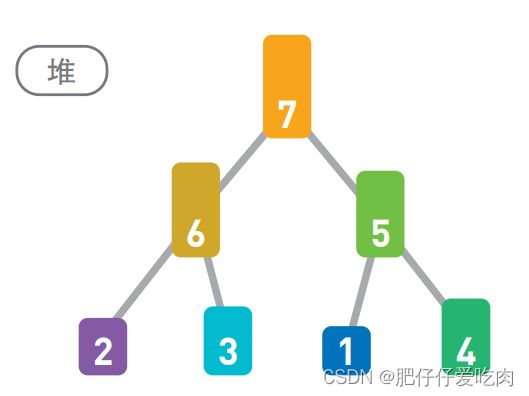
4.01这就是堆的示例。结点内的数字就是存储的数据。堆中的每个结点最多有两个子结点。树的形状取决于数据的个数。另外,结点的排列顺序为从上到下,同一行里则为从左到右。
4.02在堆中存储数据时必须遵守这样一条规则 :子结点必定大于父结点。因此,最小值被存储在顶端的根结点中。往堆中添加数据时,为了遵守这条规则,一般会把新数据放在最下面一行靠左 的位置。当最下面一行里没有多余空间时,就再往下另起一行, 把数据加在这一行的最左端。
![]()
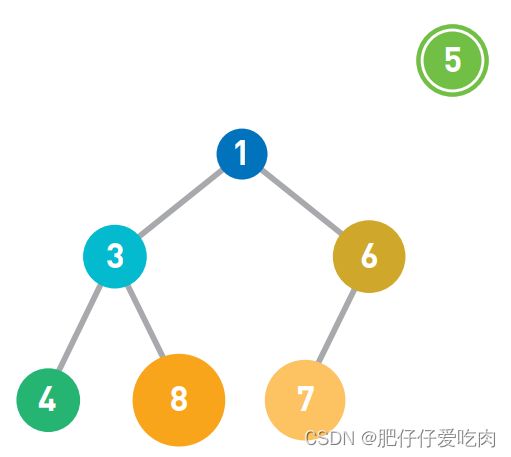
4.03我们试试往堆里添加数字5。
4.04首先按照4.02的说明寻找新数据的位置。该图中最下面一排空着一个位置,所以将数据加在此处。
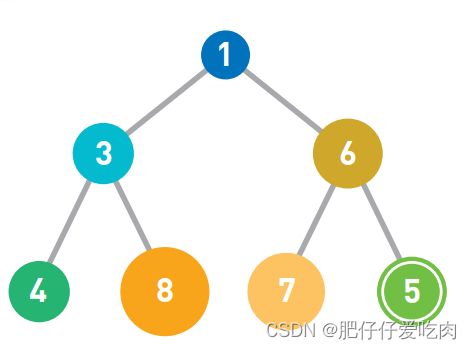
4.05如果父结点大于子结点,则不符合上文提到的规则,因此需要交换父子结点的位置。
4.06这里由于父结点的6大于子结点的5,所以交换了这两个数字。重复这样的操作直到数据都符合规则,不再需要交换为止。
![]()
4.07现在,父结点的 1 小于子结点的 5,父结点的数字更小,所以不再交换。
4.08这样,往堆中添加数据的操作就完成了。
4.09从堆中取出数据时,取出的是最上面的数据。 这样,堆中就能始终保持最上面的数据最小。
4.010由于最上面的数据被取出,因此堆的结构也需要重新调整。
4.011按照01中说明的排列顺序,将最后的数据(此处为6)移动到最顶端。
4.012如果子结点的数字小于父结点的,就将父结点 与其左右两个子结点中较小的一个进行交换。
4.013这里由于父结点的6大于子结点(右)的5大于子 结点(左)的3,所以将左边的子结点与父结点进行交换。重复这个操作直到数据都符合规则,不再需要交换为止。
4.014现在,子结点(右)的 8 大于父结点的 6 大于子结点(左)的 4,需要将左边的子结点与父结点进行交换。
4.015这样,从堆中取出数据的操作便完成了。
以上为堆的了解。
看图理解:
4.1首先,在堆中存储所有的数据,并按降序来构建堆。
4.2现在,所有数据都存进堆里了。为了排序,需要再从堆中把数据一个个取出来。
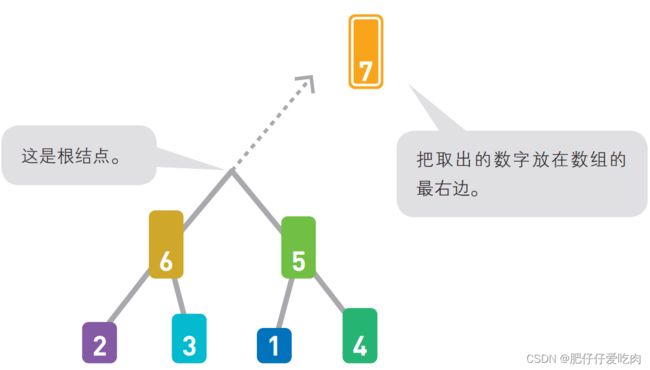
4.3我们来试一试吧。首先取出根结点的数字7。
4.4重新构造堆。
4.5同样地,取出根结点的数字6,将它放在右数 第2个位置上。
4.6重新构造堆。
4.7重复上述操作直到堆变空为止。
4.8排序中……
4.9从堆中取出了所有数字,排序完成。
![]()
核心代码:
void heapSet(int arr[], int start, int end) {
// 建立父节点指标和子节点指标
int dad = start;
int son = dad * 2 + 1;
while (son <= end) {
/* 先比较两个子节点大小,选择最大的 */
if (son + 1 <= end && arr[son] < arr[son + 1]) {
son++;
}
/* 如果父节点大于子节点代表调整完毕,直接跳出函数 */
if (arr[dad] > arr[son]) {
return;
}
else { /* 否则交换父子內容再继续子节点和父节点比较 */
int temp = arr[dad];
arr[dad] = arr[son];
arr[son] = temp;
/* 调用swap函数交换数据,效率会更高 */
//swap(arr[dad], arr[son]);
dad = son;
son = dad * 2 + 1;
}
}
}
void heapSort(int arr[], int len) {
int i;
/* 构造堆 */
for (i = len / 2 - 1; i >= 0; i--) {
heapSet(arr, i, len - 1);
}
/* 先将第一个元素和已排好元素前一位做交换,再重新调整,直到排序完毕 */
for (i = len - 1; i > 0; i--) {
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
/* 调用swap函数交换数据,效率会更高 */
//swap(arr[0], arr[i]);
heapSet(arr, 0, i - 1);
}
}测试代码:
#include
using namespace std;
int main() {
int arr[100];
int len;
cout << "请输入数组个数:";
cin >> len;
cout << "请依次输入" << len << "个数组元素,以空格分开,回车结束" << endl;
for (int i = 0; i < len; i++) {
cin >> arr[i];
}
heapSort(arr, len);
/*打印数组*/
for (int i = 0; i < len; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
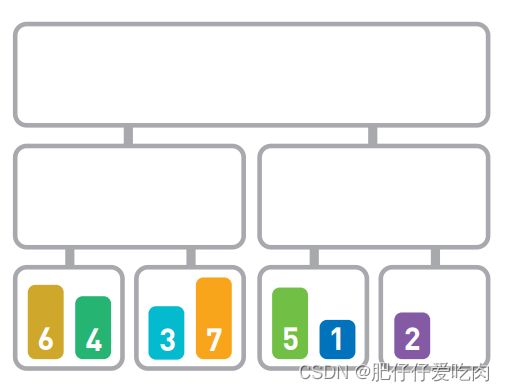
5.归并排序
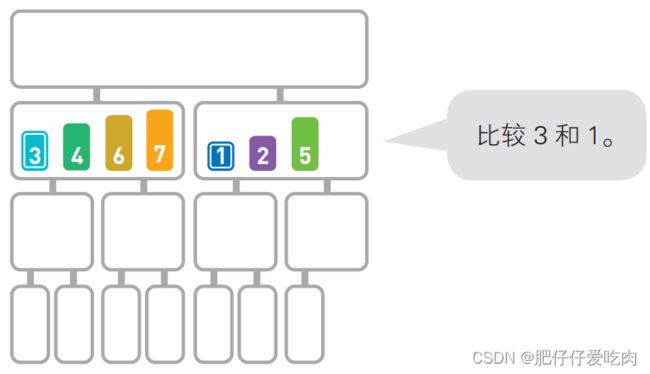
归并排序算法会把序列分成长度相同的两个子序列,当无法继续往下分时(也就是每个子序列中只有一个数据时),就对子序列进行归并。归并指的是把两个排好序的子序列合并成一个有序序列。该操作会一直重复执行,直到所有子序列都归并为一个整体为止。
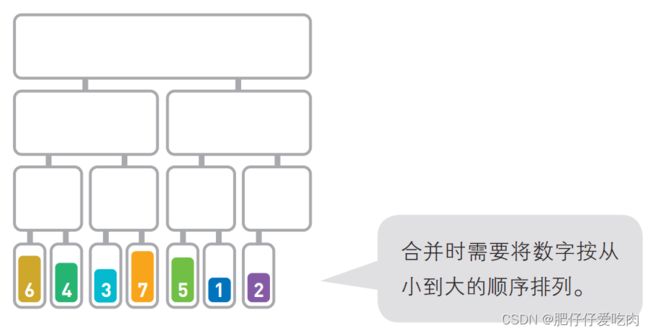
看图理解:
5.1首先,要把序列对半分割。
5.2先分成两段……
5.3再继续往下分……
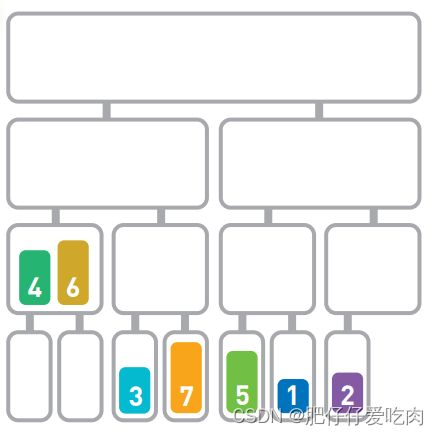
5.4分割完毕。接下来对分割后的元素进行合并。
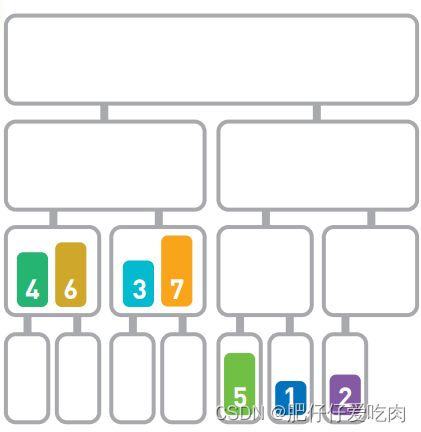
5.5把6和4合并,合并后的顺序为[4, 6]。
5.6接下来把3和7合并,合并后的顺序为[3, 7]。
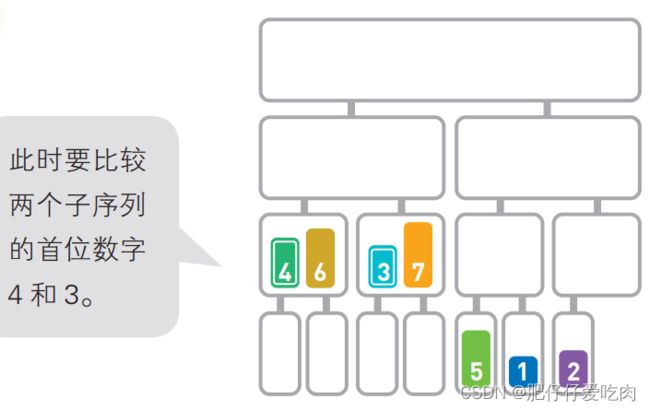
5.7下面,我们来看看怎么合并 [4, 6]和[3, 7]。合并这种含 有多个数字的子序列时,要 先比较首位数字,再移动较 小的数字。
5.8由于4>3,所以移动3。
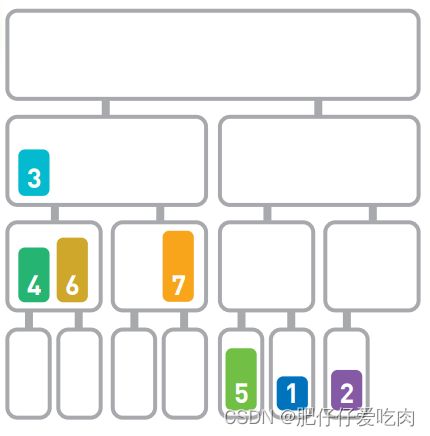
5.9同样地,再次比较序列中剩下的首位数字。
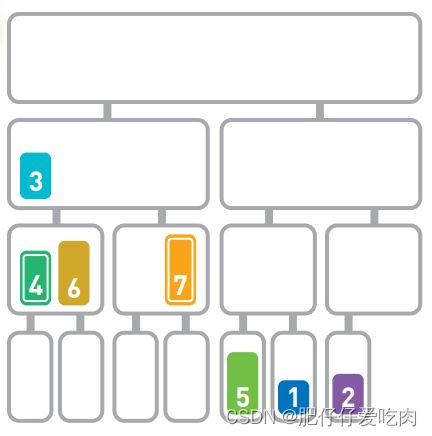
5.10由于4<7,所以移动4。
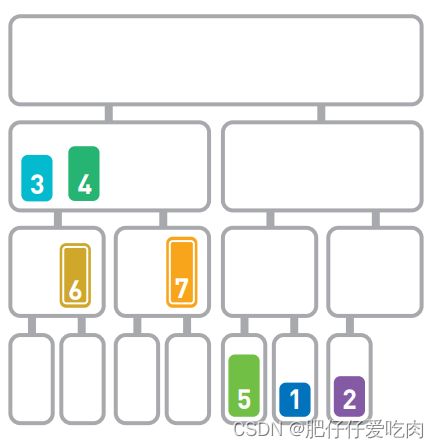
5.11由于6<7,所以移动6。
5.12最后移动剩下的7。
5.13递归执行上面的操作,直到所有的数字都合为 一个整体为止。
5.14这里也要比较两个子序列中的 首位数字。
5.15由于3>1,所以移动1。继续操作……
5.16合并完成,序列的排序也就完成了。
核心代码:
#define MAX 500000
#define SENTINEL 2000000000
int L[MAX / 2 + 2], R[MAX / 2 + 2];
void merge(int arr[], int len, int left, int mid, int right) {
int i, j, k;
int len1 = mid - left;
int len2 = right - mid;
/* 左边数据临时存储 */
for (i = 0; i < len1; i++) {
L[i] = arr[left + i];
}
/* 右边数据临时存储 */
for (i = 0; i < len2; i++) {
R[i] = arr[mid + i];
}
L[len1] = R[len2] = SENTINEL;
i = 0;
j = 0;
/* 排序合并左右两边的数据 */
for (k = left; k < right; k++) {
if (L[i] <= R[j]) {
arr[k] = L[i++];
}
else {
arr[k] = R[j++];
}
}
}
void mergetSort(int arr[],int len, int left, int right) {
if (left + 1 < right) {
int mid = (left + right) / 2;
/* 递归分左边 */
mergetSort(arr, len, left, mid);
/* 递归分右边 */
mergetSort(arr, len, mid, right);
/* 将左右两部分数据合并排序 */
merge(arr, len, left, mid, right);
}
}测试代码:
#include
using namespace std;
int main()
{
int arr[100];
int len;
cout << "请输入数组个数:";
cin >> len;
cout << "请依次输入" << len << "个数组元素,以空格分开,回车结束" << endl;
for (int i = 0; i < len; i++) {
cin >> arr[i];
}
mergetSort(arr, len,0,len);
/*打印数组*/
for (int i = 0; i < len; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
} 6.快速排序
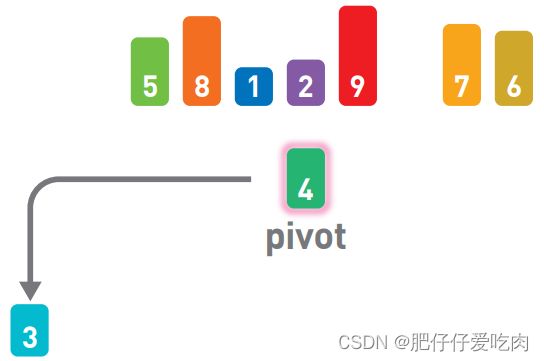
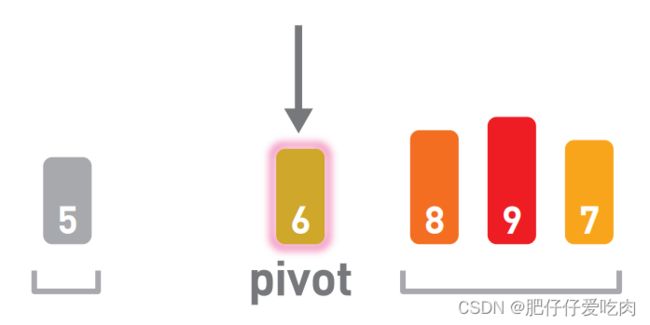
快速排序算法首先会在序列中随机选择一个基准值(pivot),然后将除了基准值以外的数分 为“比基准值小的数”和“比基准值大的数”这两个类别,再将其排列成以下形式。
[ 比基准值小的数 ] 基准值 [ 比基准值大的数 ]
接着,对两个“[ ]”中的数据进行排序之后,整体的排序便完成了。对“[ ]”里面的数据 进行排序时同样也会使用快速排序。
看图理解:
6.1下面我们就来看看快速排序的步骤。
6.2在序列中随机选择一个基准值。这里选择了4。
6.3将其他数字和基准值进行比较。小于基准值的往左移,大于基准值的往右移。
6.4首先,比较3和基准值4。
6.5因为3<4,所以将3往左移。
6.6接下来,比较5和基准值4。
6.7因为5>4,所以将5往右移。
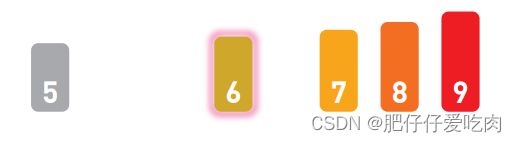
6.8对其他数字也进行同样的操作,最终结果如上图所示。
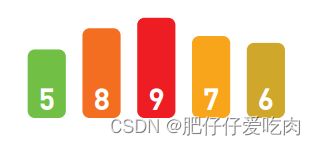
6.9把基准值 4 插入序列。这样,4 左边就是比它小 的数字,右边就是比它大的数字。
6.10分别对左边和右边的数据进行排序后,就能完 成整体的排序。
6.11两边的排序操作也和前面的一样。首先来看看 如何对右边的数据进行排序吧。
6.12随机选择一个基准值。这次选择6。
6.13把其余数据分别和基准值6进行比较,小于基 准值的就往左移,大于的就往右移。
![]()
6.14完成了大小比较和位置移动。
6.15和前面一样,对左右两边分别进行排序,进而完成整体排序。但是此时左边只有 5,所以已经是排序完 成的状态,不需要任何操作。而右边就和前面一样,先选出基准值。
6.16选择8作为基准值。
6.17将9和7分别与基准值8进行比较后,两个数字 的位置便分好了。8的两边都只有一个数据,因 此不需要任何操作。这样7、8、9便完成排序了。
6.18回到上一行,由于7、8、9完成了排序,所以 5、6、7、8、9也完成了排序。
6.19于是,最初选择的基准值4的右边排序完毕。
6.20左边也以相同的操作进行排序,整体的排序工作也就完成了。
核心代码:
int partition(int arr[], int len, int p, int r) {
int i, j;
int x;
int temp;
/* 默认x为基准值 */
x = arr[r];
i = p - 1;
/* 从下标为p到r-1进行for循环对比 */
for (j = p; j < r; j++) {
/* 以基准值x做对比,找到左边区域数据 */
if (arr[j] <= x) {
i++;
/* 交换数据,左边p开始为基准值左值区域*/
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
/* 调用swap函数交换数据,效率会更高 */
//swap(arr[i], arr[j]);
}
}
/* 别忘了将基准值放在左区域与右区域的中间 */
temp = arr[i + 1];
arr[i + 1] = arr[r];
arr[r] = temp;
/* 调用swap函数交换数据,效率会更高 */
//swap(arr[i+1], arr[r]);
/* 返回基准值所在下标 */
return i + 1;
}
void quickSort(int arr[], int len, int p, int r) {
int q;
/* 先判断是否还可以继续划分左右区域 */
if (p < r) {
/* 以基准值划分左右区域后,返回基准值下标位置q */
q = partition(arr, len, p, r);
/* 递归快排基准值左边数据 */
quickSort(arr, len, p, q - 1);
/* 递归快排基准值右边数据 */
quickSort(arr, len, q + 1, r);
}
}测试代码:
#include
using namespace std;
int main()
{
int arr[100];
int len;
cout << "请输入数组个数:";
cin >> len;
cout << "请依次输入" << len << "个数组元素,以空格分开,回车结束" << endl;
for (int i = 0; i < len; i++) {
cin >> arr[i];
}
/* 注意第三、第四个参数均为数组有效下标 */
quickSort(arr, len, 0, len-1);
/*打印数组*/
for (int i = 0; i < len; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
} 7.希尔排序
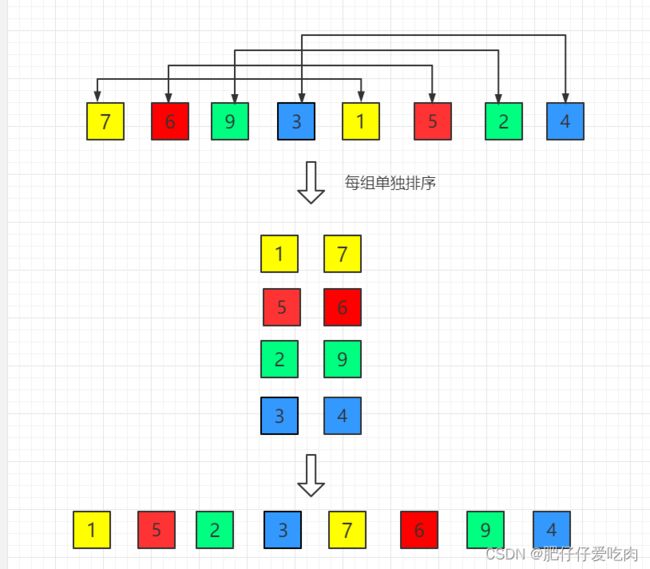
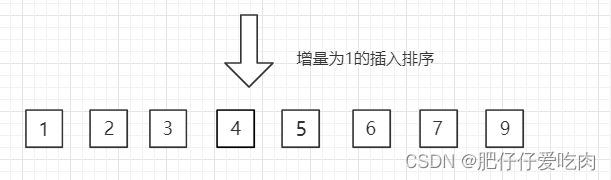
我们之前提到过插入排序算法,而希尔排序算法是充分发挥插入排序法的高速算法。希尔排序法中,程序会重复进行以间隔为g的元素为对象的插入排序。
看图理解:
1.分两组初始增量第一趟 gap = length/2 = 4。
2.第二趟,增量缩小为 2。
3.第三趟,增量缩小为 1,得到最终排序结果。
核心代码:
vector G;
/* 指定了间隔g的插入排序 */
void insertionSort(int arr[], int len,int g) {
int i, j;
int v;
for (i = g; i < len; i++) {
/* v保存的是最新待排序的数据 */
v = arr[i];
/* j为已排序区域最右端数据下标 */
j = i - g;
/* 循环比较,直到找到v待插入的位置 */
while (arr[j] > v) {
/* 待插入v数据值较小,较大数据往后移动一位 */
arr[j + g] = arr[j];
j-=g;
}
/* 此时的arr[j]>v不成立,即v下标位置为j+g */
arr[j + g] = v;
}
}
void shellSort(int arr[], int len) {
for (int h = 1;;) {
if (h > len) {
break;
}
G.push_back(h);
h = 2 * h;
}
for (int i = G.size() - 1; i >= 0; i--) {
insertionSort(arr, len, G[i]);
}
} 测试代码:
#include
#include
#include
using namespace std;
int main()
{
int arr[100];
int len;
cout << "请输入数组个数:";
cin >> len;
cout << "请依次输入" << len << "个数组元素,以空格分开,回车结束" << endl;
for (int i = 0; i < len; i++) {
cin >> arr[i];
}
shellSort(arr, len);
/*打印数组*/
for (int i = 0; i < len; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
} 8.计数排序
计数排序是一种稳定的排序算法,计数排序是一个非基于比较的排序算法,它的优势在于在对一定范围内的整数排序时,它的复杂度为Ο(n+k)(其中k是整数的范围),快于任何比较排序算法。 当然这是一种牺牲空间换取时间的做法,而且当O(k)>O(n*log(n))的时候其效率反而不如基于比较的排序。
看图理解:
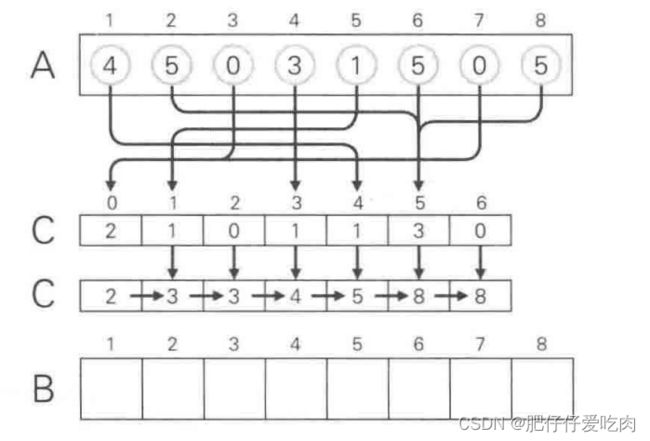
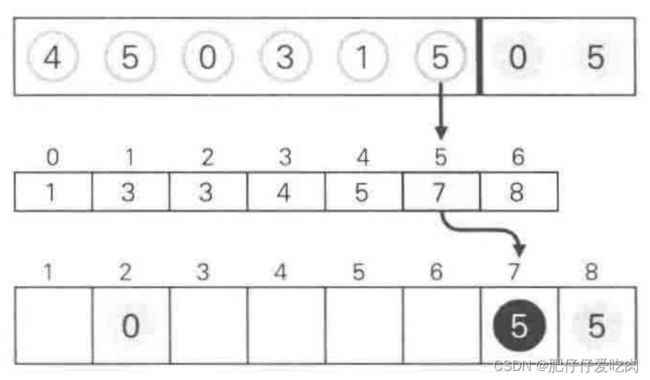
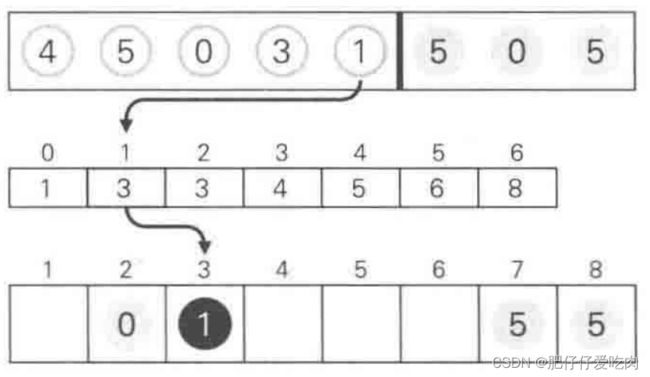
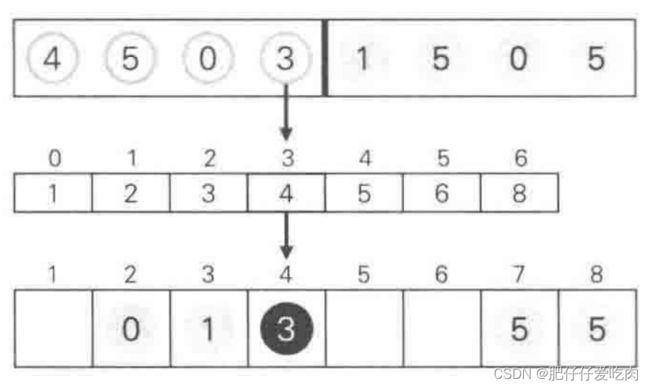
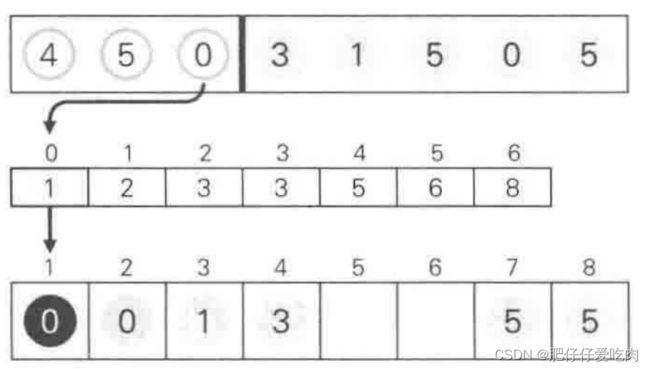
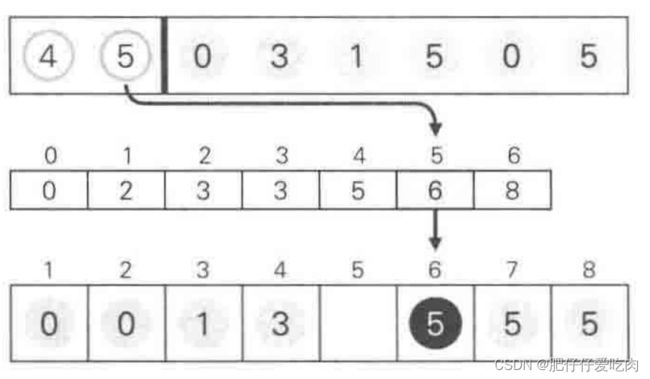
8.1找出待排序的数组中最大数据5和最小数据0,统计数组中每个值为i的元素出现的次数,存入数组C的第i项,对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加)。
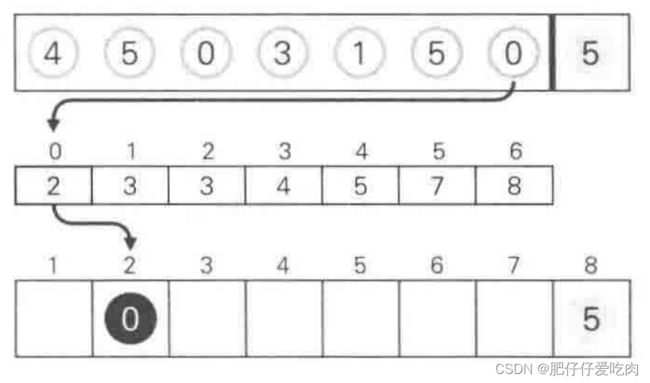
8.2 反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1,从最右边放第一个数据5。
8.3放数据0
8.4放数据5
8.5放数据1
8.6放数据3
8.7放数据0
8.8放数据5
8.9 放数据4,新数组B中数据已排序完成。
完整代码:
#include
using namespace std;
const int MAXN = 100000;
const int k = 1000; // range(范围)
int arr[MAXN],brr[MAXN];
int crr[MAXN] = { 0 };
int main() {
int len;
cout << "请输入数组个数:";
cin >> len;
cout << "请依次输入" << len << "个数组元素,以空格分开,回车结束" << endl;
for (int i = 0; i < len; ++i) {
cin >> arr[i];
crr[arr[i]]++;
}
for (int i = 1; i < k; ++i)
crr[i] += crr[i - 1];
for (int i = len - 1; i >= 0; --i)
brr[--crr[arr[i]]] = arr[i];
for (int i = 0; i < len; ++i)
cout << brr[i] << " ";
cout< 9.桶排序
桶排序的思想就是把待排序的数尽量均匀地放到各个桶中,再对各个桶进行局部的排序,最后再按序将各个桶中的数输出,即可得到排好序的数。
看图理解:
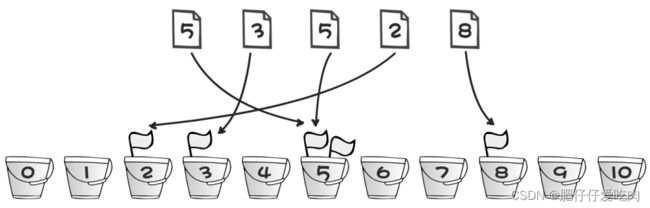
这个算法就好比有 11 个桶,编号从 0~10。每出现一个数,就在对应编号的桶中放一个小旗子,最后只要数数每个桶中有几个小旗子就 OK 了。
例如 2 号桶中有 1 个小旗子,表示 2 出现了一次;3 号桶中有 1 个小旗子,表示 3 出现了一次;5 号桶中有 2 个小旗子,表示 5 出现了两次;8 号桶中有 1 个小旗子,表示 8 出现了一次。
完整代码:
#include
using namespace std;
#define max 101
void bucketSort(int arr[], int len, int buck[]) {
for (int i = 0; i < max; i++) {
for (int j = 0; j < buck[i]; j++) {
cout << i << " ";
}
}
cout << endl;
}
int main() {
int arr[max-1];
int len;
int buck[max] = { 0 };
cout << "请输入数组个数:";
cin >> len;
cout << "请依次输入" << len << "个数组元素,以空格分开,回车结束" << endl;
for (int i = 0; i < len; i++) {
cin >> arr[i];
buck[arr[i]]++;
}
bucketSort(arr, len,buck);
return 0;
}
10.基数排序
基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数。
它是这样实现的:将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零。然后从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。
看图理解:
完整代码:
#include
#include
using namespace std;
/* 辅助函数,求数据的最大位数 */
int maxbit(int arr[], int len)
{
int maxData = arr[0];
/* 先求出最大数,再求其位数 */
for (int i = 1; i < len; ++i)
{
if (maxData < arr[i])
maxData = arr[i];
}
int d = 1;
int p = 10;
while (maxData >= p)
{
maxData /= 10;
++d;
}
return d;
}
void radixsort(int arr[], int len) {
int d = maxbit(arr, len);
int* tmp = new int[len];
int* count = new int[10];
int i, j, k;
int radix = 1;
for (i = 1; i <= d; i++) {
for (j = 0; j < 10; j++) {
/* 每次分配前清空计数器 */
count[j] = 0;
}
for (j = 0; j < len; j++){
/* 统计每个桶中的记录数 */
k = (arr[j] / radix) % 10;
count[k]++;
}
for (j = 1; j < 10; j++) {
/* 将tmp中的位置依次分配给每个桶 */
count[j] = count[j - 1] + count[j];
}
/* 将所有桶中记录依次收集到tmp中 */
for (j = len - 1; j >= 0; j--) {
k = (arr[j] / radix) % 10;
tmp[count[k] - 1] = arr[j];
count[k]--;
}
/* 将临时数组的内容复制到arr中 */
for (j = 0; j < len; j++) {
arr[j] = tmp[j];
}
radix = radix * 10;
}
delete[]tmp;
delete[]count;
}
int main()
{
int arr[100];
int len;
cout << "请输入数组个数:";
cin >> len;
cout << "请依次输入" << len << "个数组元素,以空格分开,回车结束" << endl;
for (int i = 0; i < len; ++i) {
cin >> arr[i];
}
radixsort(arr, len);
/*打印数组*/
for (int i = 0; i < len; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
参考书籍:
1.石田宝辉 宫崎修一:《我的第一本算法书》
2.渡部有隆:《挑战程序设计竞赛2》
2.啊哈磊:《啊哈!算法》
3.王晓华:《算法的乐趣》
4.托马斯.克尔曼等:《算法导论》