ELIC: Efficient Learned Image Compression with Unevenly Grouped Space-Channel Contextual Adaptive
文章目录
-
-
- ELIC: Efficient Learned Image Compression with Unevenly Grouped Space-Channel Contextual Adaptive Coding
-
- Abstract
- Introduction
- Related works
-
- Learned lossy image compression
- Backward-adaptive entropy models
- Parallel multi-dimension context modeling
- Information compaction property
-
- Unevenly grouped channel-wise context model
- SCCTX: space-channel context model
- ELIC: efficient learned image compression with scalable residual nonlinearity
-
- Stacking residual blocks for nonlinearity
- Architecture of ELIC
- Quickly decoding thumbnail-preview
- Experiments
-
- Settings
-
ELIC: Efficient Learned Image Compression with Unevenly Grouped Space-Channel Contextual Adaptive Coding
三大贡献:
一是提出了非均匀分组的空间通道联合上下文SCCTX;二是实验证明了GDN可被卷积残差块替换,
并在此基础上结合SCCTX给出了新的变换网络结构设计思路及一个设计实例ELIC,为LIC提供了新的SOTA方案;三是提出了预览图快速解码问题,并结合SCCTX的能量集中特性设计了一个快速解码网络,进一步拓展了ELIC的实用性。
论文中的实验是如何设计的?
实验是如何设计的
我们的实验主要用于验证非均匀分组SCCTX的有效性及残差块替代GDN的可行性。
实验表明,采用非均匀分组的通道上下文时,无论是否引入空间上下文,解码的网络推理速度均比均匀分组有显著提升。当引入空间上下文时,模型的率失真性能显著优于无空间上下文的模型,且非均匀分组的SCCTX解码速度比无空间上下文的均匀分组方案还要快。
当使用单个残差块替代GDN时,模型在GPU上的推理速度几乎没有变化,而率失真表现小幅度提升。这初步验证了我们的假设,即GDN可以被试做非线性层,并可被其他非线性层替代。我们推测速度的变化较小是因为卷积运算可以被BLAS库充分加速,而GDN层引入了昂贵的平方根倒数(rsqrt)。为了进一步完善实验结论,我们在CPU上重复了该实验并得到了类似的结论。我们已将相关数据报告到论文的补充材料中。当进一步堆叠残差块时,模型率失真性能得到了直接的提升,而当我们尝试堆叠GDN后,模型在训练中产生了数值稳定性问题导致训练失败。这进一步补充说明了将GDN替换为简单残差块的优势。
论文中的实验及结果有没有很好地支持需要验证的科学假设?
我们认为Q6中简述的实验结果良好的支持了Q3中所提及的科学假设:空间上下文与通道上下文存在正交性,两者可以有机结合并进一步改善LIC模型;GDN可以被替换为卷积残差块,使得模型从率失真性能、推理速度、可伸缩性以及训练稳定性四个角度获益
Abstract
Recently, learned image compression techniques have achieved remarkable performance, even surpassing the best manually designed lossy image coders. They are promising to be large-scale adopted. For the sake of practicality, a thorough investigation of the architecture design of learned image compression, regarding both compression performance and running speed, is essential. In this paper, we first propose uneven channel-conditional adaptive coding, motivated by the observation of energy compaction in learned image compression. Combining the proposed uneven grouping model with existing context models, we obtain a spatial-channel contextual adaptive model to improve the coding performance without damage to running speed. Then we study the structure of the main transform and propose an efficient model, ELIC, to achieve state-of- the-art speed and compression ability. With superior performance, the proposed model also supports extremely fast preview decoding and progressive decoding, which makes the coming application of learning-based image compression more promising.
最近,学习的图像压缩技术已经取得了显着的性能,甚至超过了最好的手动设计的有损图像编码器。它们有望被大规模采用。出于实用性的考虑,对学习图像压缩的架构设计(包括压缩性能和运行速度)进行彻底的研究是至关重要的。在本文中,我们首先提出了不均匀通道条件自适应编码,其灵感来自于学习图像压缩中能量压缩的观察。将所提出的不均匀分组模型与现有的上下文模型相结合,我们获得了空间通道上下文自适应模型,以在不损害运行速度的情况下提高编码性能。然后我们研究了主变换的结构,并提出了一种有效的模型 ELIC,以实现最先进的速度和压缩能力。凭借优越的性能,所提出的模型还支持极快的预览解码和渐进解码,这使得基于学习的图像压缩的未来应用更具前景。
Introduction
In the past years, lossy image compression based on deep learning develops rapidly [4, 5, 15, 20, 22, 24, 29, 39, 40, 49, 50].They have achieved remarkable progress on improving the rate-distortion performance, with usually much better MS-SSIM [47] than conventional image formats like JPEG [26] and BPG [8], which indicates better subjective quality. Some very recent works [18–20, 22, 49, 50] even outperform the still image coding of VVC [2], one of the best hand-crafted image and video coding standards at present, on both PSNR and MS-SSIM. These results are encouraging, as learned image compression has been proved as a strong candidate for next generation image compression techniques. In the near future, it is quite possible to deploy this line of image compression models in industrial applications. Yet, to make these approaches practical, we must carefully assess the running speed, especially the decoding speed of learned image compression
在过去的几年里,基于深度学习的有损图像压缩发展迅速[4,5,15,20,22,24,29,39,40,49,50]。他们在提高压缩率方面取得了显着的进展。失真性能,通常 MS-SSIM [47] 比 JPEG [26] 和 BPG [8] 等传统图像格式要好得多,这表明主观质量更好。一些最近的作品 [18–20, 22, 49] , 50] 在 PSNR 和 MS-SSIM 上甚至优于 VVC [2] 的静态图像编码,VVC 是目前最好的手工图像和视频编码标准之一。这些结果令人鼓舞,因为学习图像压缩已被证明下一代图像压缩技术的有力候选者。在不久的将来,很有可能在工业应用中部署这一系列图像压缩模型。然而,为了使这些方法实用,我们必须仔细评估运行速度,尤其是学习图像压缩的解码速度
One of the most important techniques in learned image compression is the joint backward-and-forward adaptive entropy modeling [15,20,22,29,39,40,48–50].It helps convert the marginal probability model of coding-symbols to a joint model by introducing extra latent variables as prior [5, 39, 40], leading to less redundancy and lower bit- rate. However, the backward-adaptive models along spatial dimension significantly break the parallelism,which inevitably slows down the decoding. To address the issue, He et al.[24]proposes to adopt checkerboard convolution as a parallel replacement to the serial autoregressive context model, which has a much better degree of parallelism with constant complexity. Minnen et al.[40]proposes to adopt a context model along channel dimension instead of the serial-decoded spatial ones, which also improves the parallelism. However, to achieve a non-trivial bit-saving with this channel-conditional model, the symbols are divided to 10groups and coded progressively, which still slows down the overall inference. It is promising to delve into parallel multi-dimension contextual adaptive coding by combing these two models to achieve better coding ability [24], constituting one of the motivation of our work. In this paper,we investigate an uneven grouping scheme to speed up the channel-conditional method, and further combine it with a parallel spatial context model, to promote RD performance while keeping a fast running speed
学习图像压缩中最重要的技术之一是联合后向和前向自适应熵建模[15,20,22,29,39,40,48–50]。它有助于转换边际概率模型通过引入额外的潜在变量作为先验[5,39,40],将编码符号转换为联合模型,从而减少冗余和降低比特率。然而,沿空间维度的后向自适应模型显著破坏了并行性,这不可避免地减慢了解码速度。为了解决这个问题,He 等人[24]提出采用棋盘卷积作为串行自回归上下文模型的并行替代,其具有更好的并行度和恒定的复杂度。Minnen等人[40]建议采用沿通道维度的上下文模型,而不是串行解码的空间模型,这也提高了并行性。然而,为了用这种通道条件模型实现非平凡的比特节省,符号被划分为 10分组并逐步编码,这仍然减慢了整体推理的速度。通过结合这两种模型来深入研究并行多维上下文自适应编码以获得更好的编码能力[24],这构成了我们工作的动机之一。在本文中,我们研究了一种不均匀分组方案来加速通道条件方法,并进一步将其与并行空间上下文模型相结合,以在保持快速运行速度的同时提高RD性能
More and more complex transform networks also slow down the inference. As learned image compression is formulated as a sort of nonlinear transform coding [3, 21], another plot improving coding performance is the development of main transform. Prior works introduce larger networks [15, 20, 22, 32], attention modules [15, 22, 33, 35] or invertible structures [37, 50] to main analysis and synthesis networks. These heavy structures significantly improve the RD performance but hurt the speed. We notice that, with a relative strong and fast adaptive entropy estimation (i.e. the above mentioned adaptive coding approaches with hyperprior and context model), we can re-balance the computation between main transform and entropy estimation, to obtain low-latency compression models. This further motivates us to promote the contextual modeling technique
越来越复杂的变换网络也会减慢推理速度。由于学习图像压缩被公式化为一种非线性变换编码[3, 21],另一个提高编码性能的方案是主变换的开发。先前的工作将更大的网络[15,20,22,32]、注意力模块[15,22,33,35]或可逆结构[37,50]引入到主要分析和综合网络中。这些重型结构显着提高了 RD 性能,但降低了速度。我们注意到,通过相对强大和快速的自适应熵估计(即上述具有超先验和上下文模型的自适应编码方法),我们可以重新平衡主变换和熵估计之间的计算,以获得低延迟压缩楷模。这进一步激励我们推广上下文建模技术
Learned image compression is growing mature and tends to be widely used, but its lack of efficiency is still a critical issue.In this paper, we contribute to this field from following perspectives:
- We introduce information compaction property as an inductive bias to promote the expensive channel- conditional backward-adaptive entropy model.Combining it with the spatial context model, we propose a multi-dimension entropy estimation model named Space-Channel ConTeXt (SCCTX) model, which is fast and effective on reducing the bit-rate.
- With the proposed SCCTX model, we further propose ELIC model. The model adopts stacked residual blocks as nonlinear transform, instead of GDN layers [4].It surpasses VVC on both PSNR and MS- SSIM, achieving state-of-the-art performance regarding coding performance and running speed (Figure 1 and Table 2).
- We propose an efficient approach to generate preview images from the compressed representation.To our knowledge, this is the first literature addressing the very-fast preview issue of learned image compression
图像压缩技术已经日趋成熟并趋于广泛应用,但其效率低下仍然是一个关键问题。在本文中,我们从以下角度为该领域做出了贡献:
- 我们引入信息压缩特性作为归纳偏差,以推广昂贵的通道条件后向自适应熵模型。将其与空间上下文模型相结合,我们提出了一种多维熵估计模型,称为空间通道ConTeXt(SCCTX)模型,该模型快速有效地降低了比特率。
- 在提出的SCCTX模型的基础上,我们进一步提出了ELIC模型。该模型采用堆叠残差块作为非线性变换,而不是 GDN 层[4]。它在 PSNR 和 MS-SSIM 方面均超过了 VVC,在编码性能和运行速度方面实现了最先进的性能(图 1 和表 2)。
- 我们提出了一种从压缩表示生成预览图像的有效方法。据我们所知,这是第一篇解决学习图像压缩的快速预览问题的文献
Related works
Learned lossy image compression
Learned lossy image compression [5, 15, 22, 24, 35, 39] aims at establishing a data-driven rate-distortion optimization (RDO) approach. Given input image x and a pair of neural analyzer ga and neural synthesizer gs, this learning- based RDO is formulated as:
学习有损图像压缩[5,15,22,24,35,39]旨在建立数据驱动的率失真优化(RDO)方法。给定输入图像 x 和一对神经分析器 ga 和神经合成器 gs,这个基于学习的 RDO 公式为:
(1)
where ˆy = ⌈ga(x)⌋ represents the discrete coding-symbols to be saved and ⌈·⌋ is the quantization operator.Balancing the estimated bit-rate R and image reconstruction distortion D with a rate-controlling hyper-parameter λ, we can train a set of neural networks ga, gs to obtain various pairs of im- age en/de-coding models, producing arate-distortion curve.
其中 ˆy = ⌈ga(x)⌋ 表示要保存的离散编码符号,⌈·⌋ 是量化运算符。通过速率控制超参数 λ 来平衡估计的比特率 R 和图像重建失真 D,我们可以训练一组神经网络 ga、gs 以获得各种图像编码/解码模型对,从而产生率失真曲线。
Ball ́e et al.[4] proposes to adopt a uniform noise estimator and a parametric entropy model to approximate the probability mass function p ˆy , so that its expected negative entropy −E[log p ˆy ( ˆy)] can be supervised as the R( ˆy) term in eq.1 in a differentiable manner with gradient-decent-based optimization.Later, the entropy model is further extended to a conditioned Gaussian form [5, 39]
鲍尔等人。 [4]提出采用均匀噪声估计器和参数熵模型来逼近概率质量函数 p ˆy ,从而使其期望负熵 −E[log p ˆy ( ˆy)] 可以监督为式中的 R( ˆy) 项1 以可微分的方式通过基于梯度下降的优化。后来,熵模型进一步扩展到条件高斯形式 [5, 39]
(2)
where the entropy parameters Θ = (μ, σ2) are calculated from extra computed or stored prior.Ball ́e et al.[5] adopts hyperprior ˆz to calculate the entropy parameters.ˆz is calculated from unquantized symbols y with a hyper analyzer ha.It can be seen as side-information introduced to the neural coder, acting as the forward-adaptive method.
其中熵参数 θ = (μ, σ2) 是根据之前额外计算或存储的值计算得出的。鲍尔等人 [5]采用超先验^z来计算熵参数。 ˆz 是使用超级分析器 ha 根据未量化符号 y 计算得出的。它可以被视为引入神经编码器的辅助信息,充当前向自适应方法。
To painlessly improve the coding efficiency, several training, inference, and encoding-time optimizing ap- proaches are proposed [23, 52, 54].They can improve the RD performance without slow down the decoding, and can be used together with various coding architectures.
为了轻松提高编码效率,提出了几种训练、推理和编码时间优化方法[23,52,54]。它们可以提高 RD 性能而不减慢解码速度,并且可以与各种编码架构一起使用。
Backward-adaptive entropy models
向后自适应熵模型
Backward-adaptive coding is also introduced to learned image compression, including spatial context models [22, 24,29,39] and channel-conditional models [40].Correlating current decoding symbols with already decoded symbols, this sort of approaches further save the bits.
A spatial context model refers to observable neighbors of each symbol vector ˆyi at the i-th location:
向后自适应编码也被引入到学习图像压缩中,包括空间上下文模型[22,24,29,39]和通道条件模型[40]。将当前解码符号与已解码符号相关联,这种方法进一步节省了比特。
空间上下文模型指的是每个符号向量 ˆyi 在第 i 个位置的可观察邻居:
(3)
(4)
where the context model gsp(·) is an autoregressive convolution [39, 42].Each context representation Φsp,i is used to jointly predict entropy parameters accompanied by the hyperprior ˆz.This approach demands symbol vectors ˆy1, …, ˆyHW to be decoded serially, which critically slows down the decoding [24, 35, 39].He et al.[24] proposes to separate the symbols into anchors and non-anchors
其中上下文模型 gsp(·) 是自回归卷积 [39, 42]。每个上下文表示 Φsp,i 用于联合预测伴随超先验 ˆz 的熵参数。这种方法需要符号向量 ^y1… ˆyHW 被串行解码,这严重减慢了解码速度[24,35,39]。He等人 [24]建议将符号分为锚点和非锚点
(5)
and adopts a checkerboard convolution as gsp(·), so the decoding of both anchors and non-anchors can be in parallel.Another scheme to perform parallel backward adaption is to reduce the redundancy among channels. Minnen et al.[40] proposes to group the symbol channels to K chunks as the channel-wise context:
并采用棋盘卷积作为gsp(·),因此锚点和非锚点的解码可以并行。执行并行后向自适应的另一种方案是减少通道之间的冗余。Minnen 等人[40]建议将符号通道分组为 K 个块作为通道上下文:
(6)
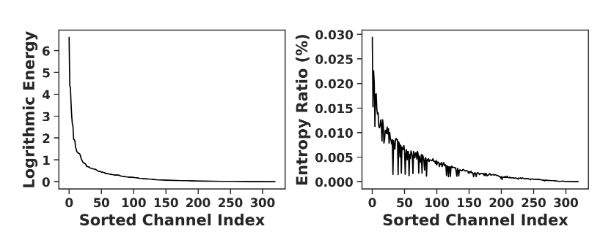
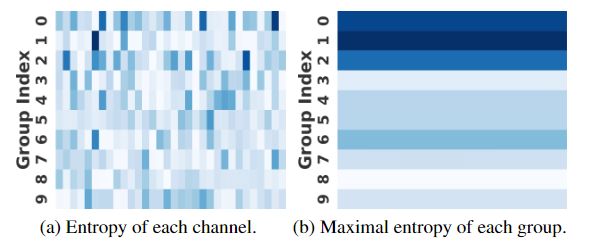
where ˆy 其中 ˆy Multi-dimension adaptive coding approaches have been proposed but all of them still suffer from the slow-speed issue, to our knowledge. Liu et al.[33] proposes a 3D context model which performs a 3D convolution passing by all the channels. Li et al.[31] proposes a multi-dimension context model with non-constant complexity. Guo et al.[22] uses 2-chunk contextual modeling with serial global-and-local adaptive coding. Ma et al.[36] propose a cross-channel context model which uses a even denser referring scheme than 3D context models 多维自适应编码方法已经被提出,但据我们所知,所有这些方法仍然存在速度慢的问题。刘等人 [33]提出了一种 3D 上下文模型,该模型执行经过所有通道的 3D 卷积。李等人[31]提出了一种具有非恒定复杂度的多维上下文模型。郭等人 [22]使用具有串行全局和局部自适应编码的2块上下文建模。马等人 [36]提出了一种跨通道上下文模型,该模型使用比 3D 上下文模型更密集的引用方案 Energy compaction is an essential property of transform coding [21], e.g.DCT-based JPEG. With decomposed coefficients extremely concentrated on lower frequencies, describing most structural and semantic information of the original image, higher frequencies can be compressed more heavily by using larger quantization steps to achieve a better rate-distortion trade-off 能量压缩是变换编码的一个基本属性[21],例如基于 DCT 的 JPEG。由于分解系数极其集中在较低频率上,描述了原始图像的大多数结构和语义信息,因此可以通过使用更大的量化步长来更严重地压缩较高频率,以实现更好的率失真权衡 We find this compaction also exists in learned analysis transform.We visualize each latent feature map ˆy(ℓ) of the mean-scale joint model, Minnen2018 [39], as its scaled magnitude (Figure 2) and draw the distribution of energy and entropy along channels (Figure 3).More strongly activated, the beginning channels have much larger average energy.Since the entropy distribution correlates to the energy distribution, it indicates an information compaction property.This phenomenon exists in all of the 5 models we test: Ball ́e2018 [5], Minnen2018 [39], Cheng2020 [15] and their parallel versions [24].The information compaction in those models is orderless because the supervision conducted on the analyzer output channels is symmetric. 我们发现这种压缩也存在于学习分析变换中。我们将平均尺度联合模型 Minnen2018 [39] 的每个潜在特征图 ˆy(ℓ) 可视化为其缩放幅度(图 2),并绘制沿通道的能量和熵分布(图 3)。起始通道的激活越强烈,其平均能量就越大。**由于熵分布与能量分布相关,因此它表明了信息压缩特性。**这种现象存在于我们测试的所有 5 个模型中:Ball ́e2018 [5]、Minnen2018 [39]、Cheng2020 [15] 及其并行版本 [24]。这些模型中的信息压缩是无序的,因为对分析器输出通道进行的监督是对称的。 Figure 2. Visualization of sorted channels with the top-10 largest average energy.Left 1: the original image (kodim19.png).Lighter regions correspond to larger symbol magnitudes |ˆy|.It can been seen from the figures that most strong activation concentrates in the first channel (left 2) and the remained channels become sparse gradually 图2:具有前 10 最大平均能量的排序通道的可视化。左 1:原始图像 (kodim19.png)。较亮的区域对应于较大的符号幅度 |ˆy|。从图中可以看出,最强的激活集中在第一个通道(左2),其余通道逐渐变得稀疏 Figure 3. Energy and entropy distribution along channels.The results are evaluated with Minnen2018 [39] model, on Kodak.The channels are sorted by energy averaged over all 24 images 图 3.:沿通道的能量和熵分布。结果在 Kodak 上使用 Minnen2018 [39] 模型进行评估。通道按所有 24 个图像的平均能量排序 When adopting a channel-conditional approach, this property induces a group-level order.See Figure 4. Particular channels in the earlier encoded groups have much larger entropy, so they are allocated more bits. As the beginning channels are more frequently referred to by following channels, the major information implicitly concentrates on the beginning channels to help eliminate more channel-wise redundancy.The progressive coding results [40] also experimentally prove this, since we can reconstruct the main semantics of images only from the beginning channels 当采用通道条件方法时,此属性会产生组级顺序。参见图 4。早期编码组中的特定通道具有更大的熵,因此它们被分配更多的比特。经常被后续通道引用,主要信息隐式地集中在开始通道上,以帮助消除更多的通道冗余。渐进编码结果[40]也通过实验证明了这一点,因为我们只能从开始通道重建图像的主要语义 We tend to understand this information compaction property of learned image compression from the perspective of sparse representation learning [41, 44, 45], yet the theoretical analysis and explanation of it are beyond the topic of this paper.We view it as a strong prior knowledge that helps us introduce inductive bias to improve the model design 我们倾向于从稀疏表示学习的角度来理解学习图像压缩的信息压缩特性[41,44,45],但其理论分析和解释超出了本文的主题。我们将其视为强大的先验知识,可以帮助我们引入归纳偏差来改进模型设计 **Figure 4.**A case study of adopting the 10-slice channel- conditional adaptive coding [40].Deeper colors denote larger values.The entropy of each channel group is implicitly sorted.The beginning groups contain channels with the largest entropy.The results are from evenly grouped model trained with λ = 0.045, evaluated on kodim08 from Kodak 图4:采用10片通道条件自适应编码的案例研究[40]。颜色越深表示值越大。每个通道组的熵是隐式排序的。开始组包含具有最大熵的通道。结果来自使用 λ = 0.045 训练的均匀分组模型,在 Kodak 的 kodim08 上进行评估 The visualization in Figure 4 shows that the later encoded channels contain less information, and they are less frequently used to predict following groups. Therefore, we can reduce the cross-group reference to speed up, by merging more later encoded channels into larger chunks.On the other hand, because of the information compaction, with less channel, the earlier encoded channel groups may still well help reduce the entropy of the following channels.Thus, a more elaborate channel grouping scheme may further improve this entropy estimation module by rebalancing the channel numbers of different groups.Yet, existing approaches often simply group the channels to chunks with the same size [22, 40] or adopt per-channel grouping [33, 36]. We propose an uneven grouping scheme, allocating finer granularity to the beginning chunks by using fewer channels and grow coarser gradually for the following chunks by using more channels. Thus, for symbols ˆy with M channels, we split them along the channel dimension to 5 chunks ˆy(1), …, ˆy(5) with 16, 16, 32, 64, M −128 channels respectively. Figure 5 shows the channel-conditional model with this uneven allocation. It only requires 5 times of parallel calculation to decode all the slices ˆy(k), which saves the running time 图 4 中的可视化显示,较晚编码的通道包含较少信息,并且它们较少用于预测后续组。因此,我们可以通过将更多稍后编码的通道合并成更大的块来减少跨组引用以加快速度。另一方面,由于信息压缩,在通道较少的情况下,较早编码的通道组仍然可以很好地帮助减少后续通道的熵。因此,更精细的信道分组方案可以通过重新平衡不同组的信道数量来进一步改进该熵估计模块。然而,现有的方法通常简单地将通道分组为具有相同大小的块[22, 40]或采用按通道分组[33, 36]。 我们提出了一种不均匀的分组方案,通过使用较少的通道为开始的块分配更细的粒度,并通过使用更多的通道为后续的块逐渐变得更粗。因此,对于具有 M 个通道的符号 ˆy,我们将它们沿着通道维度分割为 5 个块 ˆy(1),…。 。 。 , ˆy(5) 分别有 16, 16, 32, 64, M −128 个通道。图 5 显示了具有这种不均匀分配的信道条件模型。只需要5次并行计算即可解码所有切片ˆy(k),节省了运行时间 Figure 5. Proposed uneven grouping for channel-conditional (CC) adaptive coding.The M -channel coding-symbols ˆy are grouped into 5 chunks with gradually increased number of channels Ck 图 5. 针对信道条件 (CC) 自适应编码提出的不均匀分组。 M 通道编码符号 ^y 被分为 5 个块,通道数量逐渐增加 Ck Spatial context model and channel-conditional model eliminate redundancy along spatial and channel axes. As those dimensions are orthogonal, we assume the redundancy in those dimensions is orthogonal too. Thus, we combine the two models for a better backward-adaptive coding. 空间上下文模型和通道条件模型消除了沿空间和通道轴的冗余。由于这些维度是正交的,我们假设这些维度的冗余也是正交的。因此,我们结合这两个模型以获得更好的后向自适应编码。 Figure 6 shows our space-channel context model (SC- CTX).In the k-th unevenly grouped chunk, we apply a spatial context model g(k) sp to recognise spatial redundancy (eq. 4).It could be an autoregressive convolution [39] or its two-pass parallel adaption [24].We introduce gch net- works to model the channel-wise context Φ(k) ch (Figure 5 and eq. 6).The output of spatial and channel branches at the (k, i)-th location, Φ(k) sp,i and Φ(k) ch , will be concatenated with hyperprior representation Ψ and fed into a location- wise aggregation network to predictthe entropy parameters Θ(k) i = (μ(k) i , σ(k) i ) for the following en/decoding of ˆy(k) i .Then the just obtained ˆy(k) i will be used as context to com- pute Φ(k) sp,(i+1) or Φ(k+1) ch , till en/decoding the entire ˆy 图 6 显示了我们的空间通道上下文模型 (SC-CTX)。在第 k 个不均匀分组的块中,我们应用空间上下文模型 g(k) sp 来识别空间冗余(等式 4)。它可以是自回归卷积[39]或其两遍并行自适应[24]。我们引入 gch 网络来对通道上下文 Φ(k) ch 进行建模(图 5 和等式 6)。第 (k, i) 个位置处的空间和通道分支的输出 Φ(k) sp,i 和 Φ(k) ch 将与超先验表示 Ψ 连接并馈入位置明智的聚合网络以进行预测熵参数 θ(k) i = (μ(k) i , σ(k) i ) 用于以下 ˆy(k) i 的编码/解码。然后将刚刚获得的 ˆy(k) i 作为上下文来计算 Φ(k) sp,(i+1) 或 Φ(k+1) ch ,直到对整个 ˆy 进行编码/解码 Figure 6. Diagram of proposed space-channel context model As shown in Table 1, by default we use the parallel checkerboard [24] model as the spatial context for SCCTX, which is only applied inside each channel chunk to be more efficient 如表1所示,默认情况下我们使用并行棋盘[24]模型作为SCCTX的空间上下文,该模型仅应用于每个通道块内部以提高效率 For a long period, generalized divisive normalization (GDN) is one of the most frequently used techniques in learned image compression [5, 15, 22, 29, 50].It introduces point-wise nonlinearity to the model [6], which aggregates information along the channel axis and scales feature vectors at each location. Different from linear affine normalization techniques like batch normalization or layer normalization, this nonlinear GDN performs more similarly to point-wise attention mechanism. Thus, we propose to investigate other nonlinear transform layers as alternatives of GDN. Note that this is different from existing investigations that view GDN as activation function [14, 15, 17, 27]. We replace the GDN/IGDN layers with stacks of residual bottleneck blocks [25].Earlier works also investigate pure convolution networks for visual compression [11–14] and here we revisit it from the layer-level perspective. We observe that the performance further improves when the number of stacked blocks increases, because of the enhanced nonlinearity. Thus, a network with strong enough nonlinearity can express the intermediate features better for rate- distortion trade-off, even without GDN layers. A similar structure is also investigated by Chen et al.[11], as a part of non-local attention module. We experimentally prove that, even without attention mechanism, the RD performance can still be improved by simply stacking the residual blocks 长期以来,广义除法归一化(GDN)是学习图像压缩中最常用的技术之一[5,15,22,29,50]。它向模型[6]引入了逐点非线性,该模型沿着通道轴聚合信息并缩放每个位置的特征向量。与批量归一化或层归一化等线性仿射归一化技术不同,这种非线性 GDN 的表现与逐点注意力机制更相似。因此,我们建议研究其他非线性变换层作为 GDN 的替代品。请注意,这与将 GDN 视为激活函数的现有研究不同 [14,15,17,27]。 我们用残留瓶颈块堆栈替换 GDN/IGDN 层 [25]。早期的工作还研究了用于视觉压缩的纯卷积网络[11-14],在这里我们从层的角度重新审视它。**我们观察到,当堆叠块数量增加时,由于非线性增强,性能进一步提高。**因此,即使没有 GDN 层,具有足够强非线性的网络也可以更好地表达中间特征以进行率失真权衡。 Chen 等人也研究了类似的结构。 [11],作为非局部注意力模块的一部分。我们通过实验证明,即使没有注意力机制,通过简单地堆叠残差块仍然可以提高RD性能 Stacking residual blocks allows us to better conduct scalable model profiling. It is also expected to benefit from modern training and boosting techniques like network architecture search [34, 53] and loss function search [30, 46], though they are out of the bound of this work.Residual block is also easier to be extended for dynamic or slimmable inference, while GDN requires special handling [51] 堆叠残差块使我们能够更好地进行可扩展的模型分析。它还有望受益于现代训练和增强技术,如网络架构搜索 [34, 53] 和损失函数搜索 [30, 46],尽管它们超出了这项工作的范围。残差块也更容易扩展用于动态或可精简推理,而 GDN 需要特殊处理 [51] We summarize the above-mentioned techniques in our proposed model named ELIC (see Figure 7), to build an efficient learned image compression model with strong compression performance. We use the proposed SCCTX module to predict the entropy parameters Θ = (μ, σ) of a mean-scale Gaussian entropy model [39].Using this more powerful backward-adaptive coding allows adopting lighter transform networks compared with recent prior works [15, 20, 22, 50].In the main transforms, we simply adopt stride-2 convolutions to de/increase the feature map sizes, following earlier settings [5, 39] 我们在我们提出的名为 ELIC 的模型中总结了上述技术(见图 7),以构建具有强大压缩性能的高效学习图像压缩模型。我们使用提出的 SCCTX 模块来预测平均尺度高斯熵模型的熵参数 θ = (μ, σ) [39]。与最近的先前工作相比,使用这种更强大的后向自适应编码可以采用更轻的变换网络[15,20,22,50]。在主要变换中,我们简单地采用 stride-2 卷积来减少/增加特征图大小,遵循早期的设置 [5, 39] The major bottleneck of decoding process is the synthesis inference, which runs a heavy network to reconstruct the full-resolution image. When applying learned image compression, however, we do not always want to decode the full-resolution image. For instance, when looking through images saved on a server, we require the decoder to quickly generate thousands of thumbnail-preview images which have much lower resolution but keep the structure and semantics of the original images. Another case is progressive decoding preview, investigated in prior literature [40].When the image is progressively and partially decoded step by step, frequently invoking the heavy synthesizer will critically slow down the overall decoding process. On these occasions, image quality is far less important than decoding speed. Thus, directly decoding the full-resolutionimages using the heavy synthesizer is impractical 解码过程的主要瓶颈是合成推理,它运行一个重型网络来重建全分辨率图像。然而,当应用学习到的图像压缩时,我们并不总是想要解码全分辨率图像。例如,当查看服务器上保存的图像时,我们要求解码器快速生成数千张缩略图预览图像,这些图像的分辨率要低得多,但保留原始图像的结构和语义。是渐进式解码预览,在先前的文献[40]中进行了研究。当图像逐步逐步部分解码时,频繁调用繁重的合成器将严重减慢整个解码过程。在这些情况下,图像质量是远不如解码速度重要。因此,使用重型合成器直接解码全分辨率图像是不切实际的 We propose to train an additional tiny network, called thumbnail synthesizer, to reconstruct low-resolution images as thumbnail-preview. When adopting SCCTX, most semantic information is compacted in the earlier decoded channels. Hence we propose to generate the preview image only from the first 4 chunks (i.e. the first 128 channels). The structure of our proposed thumbnail synthesizer is shown in Figure 8. After training the main models, we freeze all the learned parameters and change the main synthesizer to initialized thumbnail synthesizer. Then we restart the distortion optimization to train the model. As the proposed thumbnail synthesizer is extremely light, its decoding only requires a few microseconds (w.r.t. 768 × 512 images).Compared with obtaining the preview image by down-sampling from the entirely reconstructed full-resolution image, using the proposed model to obtain the thumbnail-preview images is much more efficient. 我们建议训练一个额外的微型网络,称为缩略图合成器,以将低分辨率图像重建为缩略图预览。当采用 SCCTX 时,大多数语义信息被压缩在较早解码的通道中。因此,我们建议仅从前 4 个块(即前 128 个通道)生成预览图像。 我们提出的缩略图合成器的结构如图8所示。在训练主模型之后,我们冻结所有学习的参数并将主合成器更改为初始化的缩略图合成器。然后我们重新启动畸变优化来训练模型。 由于所提出的缩略图合成器非常轻,其解码只需要几微秒(w.r.t. 768 × 512 图像)。与通过从完全重建的全分辨率图像下采样来获取预览图像相比,使用所提出的模型来获取缩略图预览图像要高效得多。 Figure 8. Structure of the proposed thumbnail synthesizer.Bilin- ear module denotes three bilinear upsampling layers by factor 2. 图 8:所提出的缩略图合成器的结构。双线性模块表示三个双线性上采样层,因子为 2。 We train the models on the largest 8000 images picked from ImageNet [16] dataset.A noising-downsampling pre-processing is conducted following prior works [5, 24].We use Kodak [28] and CLIC Professional [1] for evaluation. The training settings are accordingly sketched from existing literature [5, 15, 24, 39].For each architecture, we train models with various λ standing for different quality presets. We set λ = {4, 8, 16, 32, 75, 150, 300, 450}×10−4 for each model when optimizing MSE. Empirically, on Kodak, models trained with these λ values will achieve average bits-per-pixel (BPP) ranging from 0.04 to 1.0.We set the number of channels N = 192 and M = 320 for all models. We train each model with an Adam optimizer with β1 = 0.9, β2 = 0.999.We set initial learning-rate to 10−4, batch-size to 16 and train each model for 2000 epochs (1M iterations, for ablation studies) or 4000 epochs (2M iterations, to finetune the reported ELIC models), and then decay the learning-rate to 10−5 for another 100-epoch training. 我们在从 ImageNet [16] 数据集中挑选的最大 8000 张图像上训练模型。噪声下采样预处理是按照先前的工作[5, 24]进行的。我们使用 Kodak [28] 和 CLIC Professional [1] 进行评估。 训练设置相应地从现有文献中勾勒出来[5,15,24,39]。对于每种架构,我们训练具有代表不同质量预设的各种 λ 的模型。在优化 MSE 时,我们为每个模型设置 λ = {4, 8, 16, 32, 75, 150, 300, 450}×10−4。根据经验,在 Kodak 上,使用这些 λ 值训练的模型将实现 0.04 到 1.0 之间的平均每像素位数 (BPP)。我们为所有模型设置通道数 N = 192 和 M = 320。我们使用 Adam 优化器(β1 = 0.9、β2 = 0.999)训练每个模型。我们将初始学习率设置为 10−4,批量大小设置为 16,并将每个模型训练 2000 轮(1M 迭代,用于消融研究)或 4000 轮(2M 迭代,以微调报告的 ELIC 模型),然后对于另一个 100 时期的训练,将学习率衰减到 10−5。Parallel multi-dimension context modeling
Information compaction property
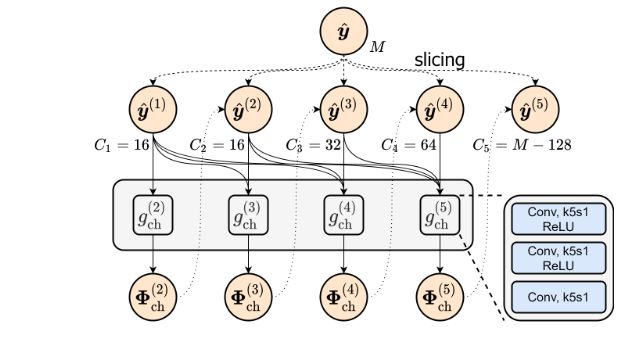
Unevenly grouped channel-wise context model
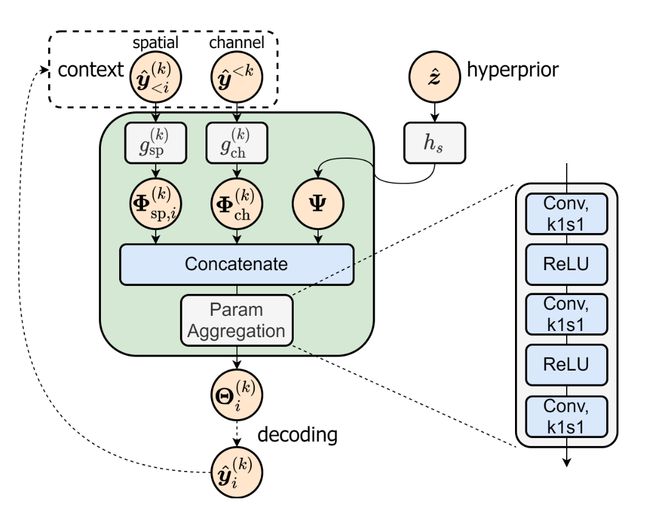
SCCTX: space-channel context model
ELIC: efficient learned image compression with scalable residual nonlinearity
Stacking residual blocks for nonlinearity
Architecture of ELIC
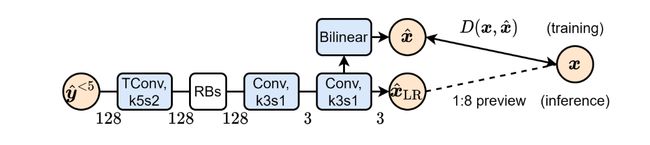
Quickly decoding thumbnail-preview
Experiments
Settings