编译原理学习笔记

引论

什么是编译程序

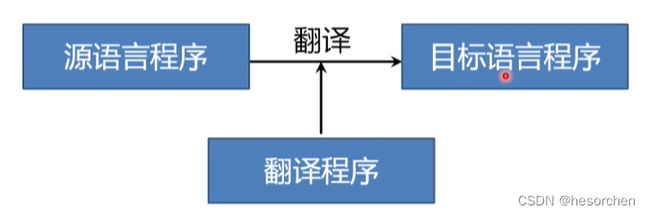
翻译程序：把某一种语言程序（源语言程序）等价地转换成另一种语言程序（目标语言程序）的程序。

编译程序：编译程序也是一种翻译程序，把某一种高级语言等价的转换为另一种低级语言程序（如汇编语言或机器语言程序）的程序。

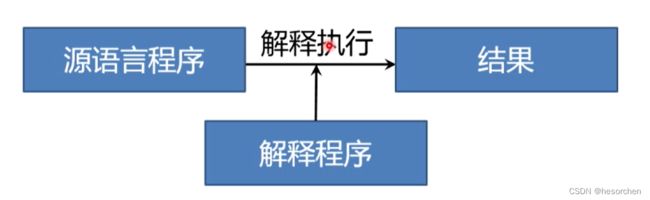
解释程序：解释程序也是一种翻译程序，把源语言的源程序作为输入，但不产生目标程序，而是边解释边执行源程序。

为什么要学习编译原理

从计算机科学与技术中学什么？

一系列广泛的计算机科学的思维方法：

• 抽象
• 自动化
• 问题分解
• 递归
• 权衡
• 保护、冗余、容错、纠错、恢复
• 利用启发式推理来寻求解答
• 在不确定情况下的规划、学习和调度
  … …

这些方法在日常生活中也会产生作用。

编译原理是理论和实践相结合的最好典范。

抽象

• 忽略一个主题中与当前问题（或目标）无关的那些方面，以便更充分地注意与当前问题（或目标）有关的方面

• 以众多的事物中抽取出共同、本质性的特征，舍弃其非本质的特征

• 是一种从个体把握一般、从现象把握本质的认知过程和思维方法

• 图灵机

自动化

• 有限自动机、预测分析程序、算符优先分析、LR分析

问题分解

• 将大规模的复杂问题分解成若干个较小规模、更简单的问题加以解决

• 层次化管理

• 编译程序引入中间语言

• 编译过程分成多个阶段（语法分析、词法分析等）

递归

• 问题的解决依赖于类似问题的解决，只不过后者的复杂度更小

• 一旦将问题的复杂程度和规模化简化到足够小时，问题的解法非常简单。

• 递归下降分析法

• 基于树遍历的属性计算

• 语法制导翻译

权衡

• 理论可实现 VS 实际可实现

• 理论研究重在探寻问题求解的方法，对于理论成果的研究运用有需要在能力和运用中做出权衡

• 用上下文无关文法来描述和处理高级程序语言

• 优化措施的选择

编译原理的应用

Html、xml分析、语言处理工具、Shell、http、SQL、翻译

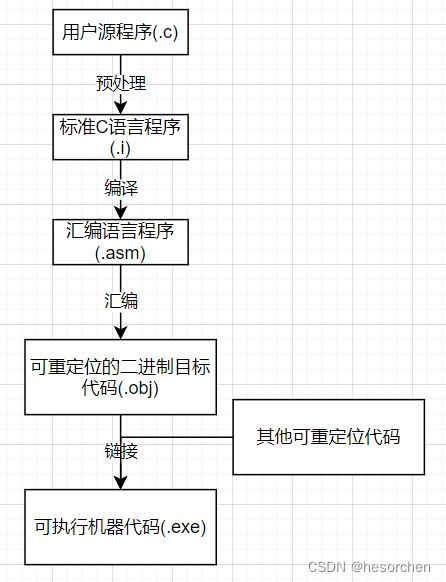
编译过程

用中英文翻译类比

中英文翻译	编译
识别出句子中的一个个单词	词法分析
分析句子的语法结构	语法分析
根据句子的含义进行初步翻译	语义分析、中间代码生成
对译文进行修饰	优化
写出最后的译文	目标代码产生

编译程序的结构

编译程序总框

遍

所谓“遍”，是指对程序扫描一遍。

阶段与遍是不同的概念

一遍可以包含若干个阶段 - 词法分析、语法分析
一个阶段也可以分成多遍 - 优化

编译前后端

• 前端

与源语言有关，如词法分析，语法分析，语义分析与中间代码产生，与机器无关的优化

• 后端

与目标机有关的优化，目标代码的产生

• 带来的好处

可移植性更强、程序逻辑结构清晰

高级程序设计语言概述

常用的高级程序设计语言

语言	特点
Fortran	数值计算
Cobol	事务处理
Pascal	结构化程序设计
Lisp	函数式程序设计
Prolog	逻辑程序设计
C	系统程序设计
Smalltalk	面向对象程序设计
Java	Internet应用
Python	解释型语言

相对于机器语言或汇编语言，高级程序设计语言。

• 更接近于数学语言和工程语言，更直观、自然和易于理解
• 更容易验证其正确性
• 编写程序的效率更高
• 更容易移植

程序设计语言的定义

• 词法规则

一般包括：常数、标识符、基本字、算符、界符等

描述工具：有限自动机

• 语法规则

语法单位通常包括：表达式、语句、分程序、过程、函数、程序等

描述工具：上下文无关文法

E -> i ：一个标识符可以单独构成一个算术表达式

E -> E + E：一个算术表达式可以由两个算术表达式构成

E -> E * E：一个算术表达式可以由两个算术表达式构成

E -> (E)：一个算术表达式加上括号还是一个算术表达式

高级程序设计语言的一般特性

高级语言的分类

• 过程式语言
• 应用式语言
• 基于规则的语言
• 面向对象的语言

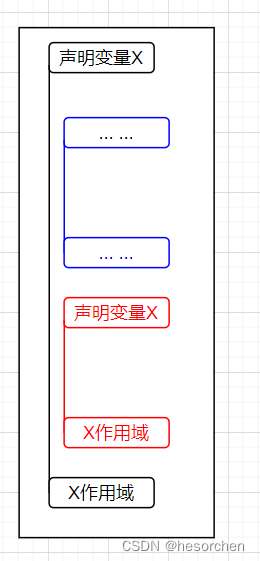
最近嵌套原则

1. 一个在子程序B1中说明的名字只在B1中有效
2. 如果B2是B1的一个内层子程序且B2中对标识符X没有新的说明，则原来的名字X在B2中仍然有效。【蓝色部分】
3. 如果B2对X重新做了说明，那么，B2对X的任何引用都是指重新说明过的这个X。【红色部分】

数据类型与操作

数据类型三要素

• 数据对象的属性
• 数据对象的取值
• 可用于数据对象的操作

常见语句类型：

1. 数值类型
   整形、浮点型
   可使用+、-、*、/

2. 布尔类型
   true、false
   可使用&、|

标识符与名字

名字的绑定是指将标识符与所代表的程序数据或代码进行关联

静态绑定：在编译过程中的绑定称为静态绑定。如声明一个整形变量。
动态绑定：在运行时的绑定称为动态绑定。如C++中的多态性、虚函数。

• 标识符

语法概念

以字母开头的，由数字和字母组成的字符串。

• 名字

语义概念

名字有确切的意义和属性。

数据结构

• 数组

数组是有同一类型数据组成的某种n维矩形结构，沿着每一维的距离，称为下标。

编译时确定长度的称为不可变数组，否则称为可变数组。

还分为按行存放、按列存放。

• 记录

由已知的数据组合在一起的一种结构

record{
   char name[20];
   interger age;
}cards[1000];

访问：cards[k].name

其他常用数据结构：字符串、栈、队列、表格、链表等。

表格：本质上是记录数组

抽象数据类型

对类型对象的封装，即，除了使用类型中所定义的运算外，用户不能对这些对象进行操作。

高级程序设计语言的语法描述

上下文无关文法

• 字母表：一个有穷字符集，记为$\Sigma$

• 字母表中每个元素称为字符

• $\Sigma$上的字（也叫字符串）是指由$\Sigma$中的字符所构成的一个又穷序列。

• 不包含任何字符的序列称为空字，记为 $\epsilon$

• $\Sigma$* 表示$\Sigma$上的所有字的全体，包含$\epsilon$

例如， $\Sigma$={a，b}，则 $\Sigma$={$\epsilon$，a，b，aa，ab，ba，bb，aaa，… …}*

• $\Sigma$*的子集$U$和$V$的连接（积）定义为$UV$={$\alpha \beta$|$\alpha \in U\&\beta \in V$}

例如，$U$={$a，b$}，$V$={$c，d$}，则$UV$={$ac，ad，bc，bd$}

• 一个字符集 $V$ 的$n$次积记作 $V^n=VV...V$（共n个$V$）。特别的，$V^0$={$\epsilon$}

• $V$ *是$V$的闭包：$V$ * = $V^0 \cup V^1 \cup V^2 \cup … … $

• $V$+是$V$的正规闭包：$V$+ =$VV$ *

闭包与正规闭包的区别：假设V中不包含空字 $\epsilon$，那么闭包中包含空字，而正规闭包中不包含空字

上下文无关文法G是一个四元组 $G=(V_T,V_N,S,P)$，其中

$V_T$：终结符（Terminator）集合
$V_N$：非终结符（Nonterminator）集合
$P$：产生式
$S$：文法开始的符号，这是一个特殊的非终结符

一般约定：

1. 第一条产生式的左部是开始符号。
2. 用大写字母表示非终结符，小写字母表示终结符
3. 设文法G开始符号为S，我们可以将文法写成G[S]
4. 为了简洁，将相同左部的多个产生式，右部用“|”符号连接

有时候不需要将文法G的四元组显式地表示出来，只将产生式写出即可。因为产生式中已经包含了所有非终结符、终结符。

下面几种文法的表示方法都是等价的：

G=({S,A},{a,b},P,S)
其中P：
    S -> Ad
    A -> a
    A -> b
    A -> c

G[S]:
    S -> Ad
    A -> a
    A -> b
    A -> c

G[S]:
    S -> Ad
    A -> a|b|c

文法与语言

推导

推导：将某个非终结符用某个产生式的右部进行替换展开，直到产生式中全部为终结符为止，这个过程称为推导。

对文法G(E):E->E+E|E*E|i|(E)进行推导：

$E\Rightarrow E+E\Rightarrow i+E\Rightarrow i+i$

句型、句子和语言

• 文法G推导过程中产生的所有符号串称为句型。
• 仅包含终结符的句型称为句子。
• 所有句子的集合称为文法G的语言。

证明i*(i+i)是文法E->(E)|E*E|E+E|i的一个句子：

$E\Rightarrow E\ast E\Rightarrow E\ast (E)\Rightarrow E\ast (E+E)\Rightarrow i\ast (E+E)\Rightarrow i\ast (i+E)\Rightarrow i\ast (i+i)$

利用递归思维，解决 给出语言求文法、给出文法求语言 相关问题：

• 请求出{$a^n{b}^n|n>0$}的文法
• 请求出文法G(E):
  E -> ab
  E -> aEb
  产生的语言

语法树与二义性

最左推导和最右推导

从一个句型到另一个的推导往往不唯一

$E\Rightarrow E+E\Rightarrow i+E\Rightarrow i+i$

$E\Rightarrow E+E\Rightarrow E+i\Rightarrow i+i$

最左推导：任何一步推导都是对当前句型中的最左非终结符进行替换

最右推导：任何一步推导都是对当前句型中的最右非终结符进行替换

语法树

$E\Rightarrow E\ast E\Rightarrow E\ast (E)\Rightarrow E\ast (E+E)\Rightarrow i\ast (E+E)\Rightarrow i\ast (i+E)\Rightarrow i\ast (i+i)$

以下是上述文法的语法树

最左推导和最右推导最后得到的语法树是一样的，只不过生长顺序不同。

二义性：

• 文法的二义性：如果一个文法存在某个句子对应两颗不同的语法树，则说这个文法是二义的。

• 语言的二义性：如果能找到一个二义性的、能产生该语言的文法，该语言是二义的。

形式语言鸟瞰

0/1/2/3型文法，四种文法都包含终结符、非终结符、开始符号，但是对产生式的限制不一样。

词法分析

词法分析的概述

词法分析器的功能：输入源程序，输出单词符号。

词法分析器的输出

输出的单词符号的表示形式：二元组（单词种别，单词自身的值）

单词种别通常用整数编码表示。

如果该单词种别只有一个单词，那么只需要知道单词种别就能唯一确定单词符号。

理论上可以一遍遍历来进行词法分析。但是实际上，词法分析器由语法分析器来驱动，语法分析器需要某个单词时，再由词法分析器去分析。

词法分析器的设计

预处理子程序：剔除无用的空格、回车、换行等字符。

扫描缓冲区：两个半区互补使用，一个半区的长度为该语言限制的最大单词长度。这样能保证一个单词肯定能在两个半区内找到。

超前搜索

有时候需要超前往后处理，才能处理出标识符。

解决方法：

1. 将基本字设置为保留字，用户不能用他们作为标识符。

2. 基本字作为特殊的标识符，设置保留字表。

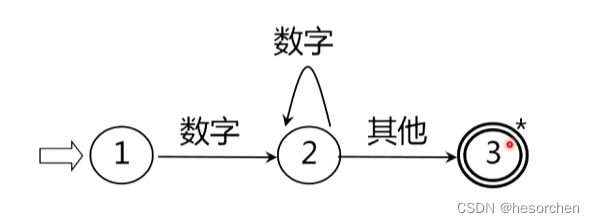
状态转换图

结点表示状态，用圆圈表示

状态之间用箭弧连接，箭弧上的字符表示输入的字符和字符类。

一张转换图只包含有限个状态，其中有一个为初态，用箭头标识，至少一个为终态，用双圈标识。

状态转换图可用于识别一定的字符串。

若存在一条从初态到某一终态的道路，且这条路上所有弧上的标记符连接成的字等于字符串$\alpha$，那么称$\alpha$被该状态转换图接受。

正规式和正规集

正规集可以用正规式表示
正规式是表示正规集的一种方法

假定$e_1$和$e_2$都是$\Sigma$上的正规式，他们所表示的正规集为$L(e_1)$和$L(e_2)$，则

• $(e_1|e_2)$ 为正规式，他所表示的正规集为$L(e_1)\cup L(e_2)$
• $(e_1\cdot e_2)$ 为正规式，他所表示的正规集为$L(e_1)L(e_2)$
• $(e_1)$* 为正规式，他所表示的正规集为$L(e_1)$*

正规式的等价性

若两个正规式所表示的正规集相同，则称这两个正规式等价。

如$b(ab)$* = $(ba)$*$b$

确定性有限状态自动机

确定性有限状态自动机是对状态图的一种形式化定义。

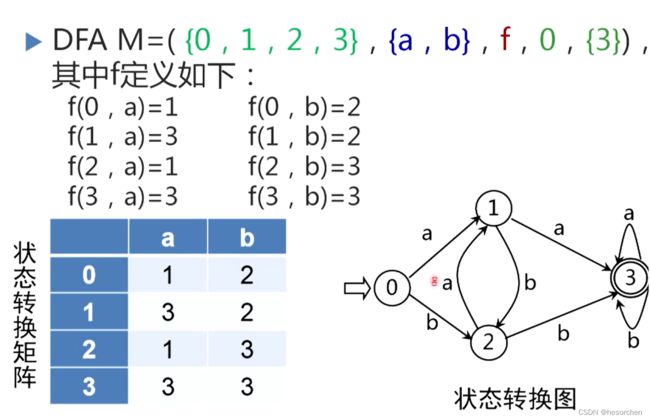
确定性有限自动机M是一个五元式 $M=(S,\Sigma ,f,S_0,F)$，其中：

• $S$ ：有穷状态集

• $\Sigma$：输入字母表

• $f$：状态转换函数，为$S \times \Sigma $ ->$S$的单值部分映射，$f(s,a)=s^{\prime }$表示：先行状态为$s$，输入字符为$a$时，状态转换为$s^{\prime }$，$s^{\prime }$为$s$的一个后继状态。

• $S_0$：$S_0\in S$，表示初态。

• $F$：$F\in S$，表示终态，可以为空。

DFA表示为状态转换图：

• 假定DFA M含有m个状态和n个输入字符
• 对应的状态转换图含有m个状态结点，每个结点顶多含有n条箭弧射出，且每条箭弧用$\Sigma$上的不同的输入字符来做标记。

若存在一条从初态到某一终态的道路，且这条路上所有弧上的标记符连接成的字等于字符串$\alpha$，那么称$\alpha$被该DFA M接受。

非确定性有限状态自动机

非确定性有限自动机M是一个五元式 $M=(S,\Sigma ,f,S_0,F)$，其中：

• $S$ ：有穷状态集

• $\Sigma$：输入字母表

• $f$：状态转换函数，为$S \times \Sigma $ ->$S$的单值部分映射，$f(s,\alpha )=s^{\prime }$表示：先行状态为$s$，输入字为$\alpha$时【而非一个字符】，状态转换为$s^{\prime }$，$s^{\prime }$为$s$的一个后继状态。

• $S_0$：$S_0\in S$，表示初态集。

• $F$：$F\in S$，表示终态，可以为空。

与确定性状态自动机的区别：

• NFA的箭弧上，可以是字符、字、正规集，DFA只能是字符。

• NFA的初始态可以有多个，另一者最多一个。

• DFA是NFA的一个特例。

若存在一条从某个初态到某一终态的道路，且这条路上所有弧上的标记符连接成的字等于字符串$\alpha$，那么称$\alpha$被该NFA M接受

DFA与NFA

如果两个有限自动机$M_1$和$M_2$，如果L(M)=L(M’)，则称M与M’等价。

自动机理论中有一个重要的结论：判定两个自动机等价性的算法是存在的

DFA与NFA识别能力相同

对于每个NFA $M_1$都存在一个DFA $M_2$与之等价。

DFA与NFA的等价性证明

对NFA进行改造：

• 引入新的初态结点X和终态结点Y，从初态结点X到所有NFA上的初态结点射出一条$\epsilon$弧，所有NFA上的终态结点射出一条$\epsilon$弧到终态结点Y。这样就使得该NFA只有一个初态结点和终态结点。

• 引入中间状态，对字进行拆解。

NFA确定化-子集法

用于解决$\epsilon$弧和转换关系

设 $I$ 是状态集的一个子集，定义 $I$ 的$\epsilon$-闭包 为$\epsilon$-closure(I)

即 $I^{\prime }$ = $\epsilon$-closure(I)，且状态集 $I^{\prime }$ 由状态集 $I$ 经过若干条$\epsilon$弧转换而来。

$I_a$运算：$I_a$ = $\epsilon$-closure(J)。其中状态集$J$为状态集$I$经过一条$a$弧到达的状态集。

状态集的转换表

用新的状态表示来替换原来的状态集，得到DFA：

DFA的化简

对于给定的DFA M，寻找一个状态数比M少的DFA M’，使得L(M)=L(M’)

• 状态的等价性
  假设s和t为M的两个状态，称s和t等价：如果从状态s出发能读出某个字$\alpha$而停止于终态，那么同样，从t出发也能读出$\alpha$而停止于终态；反之亦然。

把状态集划分为一些不相交的子集，使得任意两个不同子集的状态是可区别的，而同一子集的任何两个状态是等价的。这样每个子集选出一个代表，可以使得DFA最小化。

假定状态$s_1$和$s_2$当前是两个不可区别的状态，并且他们经过一条弧$a$可以到达两个可区别的状态$t_1,t_2$（即$t_1,t_2$分属两个不同的子集）那么$s_1$和$s_2$就可以划分为两个不同的子集。原因如下：

• 因为状态$t_1,t_2$分属两个子集，那么说明存在一个字$\alpha$，$t_1$读入$\alpha$之后到达终态，而$t_1$读入$\alpha$之后不能到达终态，或者反之。那么对于字$a\alpha$，状态$s_1,s_2$同理。

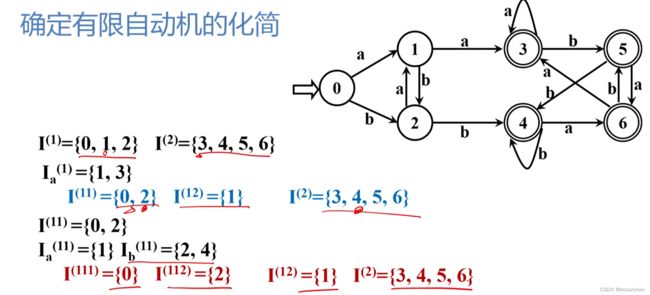
化简过程如下：

首先作初始划分，将DFA中的状态分为终态集和非终态集。
得到{I1,I2,I3 ...} {I4,I5,I6 ...}
依次考察每个子集中的状态，读入字符集中的某个字符是否可以区分该子集。
可区分则划分该集合。
循环考察，直到所有集合都不可再划分。
每个子集选出一个状态来取代所有状态。化简完成。

正规式与有限自动机的等价性

一个正规式r与一个有限自动机等价：L®=L(M)

L®：一个正规式的正规集
L(M)：有限自动机M能生成的字集

定理：对于任意的NFA M，都存在一个正规式r与之等价。

使用以下三条规则，为NFA构造对应的正规式：

将所有弧和状态消除，仅保留状态$X、Y$之后，$X$到$Y$上的弧就是该NFA 对应的正规式。

定理：对于任意的正规式r，都存在一个NFA M与之等价。

使用以下三条规则，为正规式构造对应的NFA：

关键点：构造几个相互独立的NFA，用$\epsilon$连接起来。

语法分析——至上而下分析

自上而下分析的基本问题

句子、句型和语言

• 文法G推导过程中产生的所有符号串称为句型。
• 仅包含终结符的句型称为句子。
• 所有句子的集合称为文法G的语言。

语法分析器的功能

• 按照文法的产生式，识别输入字是否是合法程序

语法分析器的地位

• 在编译器中占主导地位

自上而下(Top-down)分析法

• 从文法的开始符号出发，反复使用各种产生式，寻找"匹配"的推导
• 推导:根据文法的产生式规则，把串中出现的产生式的左部符号替换成右部
• 从树的根开始，构造语法树
• 递归下降分析法、预测分析程序

自下而上(Bottom-up)分析法

• 从输入串开始，逐步进行归约，直到文法的开始符号
• 归约:根据文法的产生式规则，把串中出现的产生式的右部替换成左部符号
• 从树叶节点开始，构造语法树
• 算符优先分析法、LR分析法

自上而下分析面临的问题：

1. 回溯问题：某个产生式左部有多个匹配的右部时，当前选择的匹配可能是错误的，需要回溯重新匹配。

2. 文法左递归问题：可能出现树无限生长的情况。

消除文法左递归

直接左递归的消除
核心思想：观察左递归产生式生成规律，借助新非终结符、右递归来消除。

间接左递归的消除
核心思想：先进行代换，然后转换成了直接左递归，用上面的方法进行直接左递归的消除。

A -> Bc|c
B -> Cd|d
C -> Aa|a
将C代入B，得到
A -> Bc|c
B -> Aad|aa|d
将B代入A，得到
A -> Aadc|aac|dc|c
消除直接左递归，得到
[消除思路]：观察发现该文法必然以aac或dc或c开头,连接若干个adc。
A -> aacA'|dcBA'|cBA'
A' -> adcA'|空字

消除回溯

回溯的产生是因为对于某个非终结符的多个候选式，可能有相同的前缀，导致不一定能选择出正确的候选式。可以使用提取公共左因子的方法进行消除：

A -> aa|ab|ac|bx|by|bz
提取因子a，得到
A -> aA'|bx|by|bz
A' -> a|b|c
提取因子b，得到
A -> aA'|bB'
A' -> a|b|c
B' -> x|y|z

First集

令G是一个不含左递归的文法，对G的所有非终结符的每个候选式$A$定义他的终结首符集$First(A)$为：

$$First(A)=a|A{\Rightarrow }^{\ast }a...\&a\in V_T$$

用人话说，$First$集是候选式$A$最后推导出的所有可能的字的第一个字符的集合。好像还是很毒瘤

这名字至少起的还行：
终结 - 最后推导出的所有可能的字
首 - 第一个
符 - 字符
集 - 集合

特别的，$\epsilon$也可以在first集中。

First集的构造算法

理解算法的核心：把握好First集合的意义——如果选择当前该文法符号，所有可能的终结字的first字符的集合。

对于每一个文法符号，连续使用下面的规则，直至每个First集合不再增大为止：

1. 若$a\in V_T$，则$First(a)=\{a\}$【我本身是终结符，first集合当然只有我自己】
2. 如果$X\in V_N$，$a\in V_T$，且有产生式$X\to a...$ ，则把$a$加入到$First(X)$中；若还有产生式$X\to \epsilon$，则把$\epsilon$也加入到$First(X)$中。【候选式的第一个字符就是终结符，再怎么折腾first字符也只能是这个字符】
3. 若$X\to Y...$ ，$X\in V_N,$$Y\in V_N$，则把$First(Y)$中的所有非$\epsilon$元素全部加入$First(X)$中。【之所以不能加入$\epsilon$，是因为Y后面可能有终结符】
4. 若$X\to Y_1{Y}_2...Y_{i-1}{Y}_i...Y_k$ ，$X\in V_N,$$Y\in V_N$，对于任何$j$，$1\le j\le i-1$，$First(Y_j)$中都含有$\epsilon$，则把$First(Y_i)$中的所有非$\epsilon$元素全部加入$First(X)$中。【我前面的都取$\epsilon$，那么我就可能作为First】如果对于所有的$First(Y)$都含有$\epsilon$，则把$\epsilon$加入到$First(X)$中。【这种情况下，所有非终结符都取$\epsilon$，最终就能得到$\epsilon$】

Follow集

令G是一个不含左递归的文法，对G的所有非终结符的每个候选式$A$定义他的$First(A)$集为：

$$Follow(A)=a|A{\Rightarrow }^{\ast }...Aa...\&a\in V_T$$

用人话说，$Follow$集是候选式$A$推导结束之后的字的后面的一个非终结符的可能的集合。

Follow集的构造算法

1. 对于文法的开始符号$S$，将#加入到$Follow(S)$中。【#表示句子的结尾，S作为开始符号，S产生的必然是一个句子，他后面自然是#】

2. 若$A\to \alpha B\beta$是一个产生式，则把除了$\epsilon$的$First(\beta )$字符加入到$Follow(B)$中。【显然】

3. 若$A\to \alpha B$是一个产生式，或$A\to \alpha B\beta$是一个产生式且$\epsilon \in First(\beta )$，则把 $Follow(A)$的字符加入到$Follow(B)$中。【第一种情况：产生式右部以B结尾，因此，A的follow必然可以是B的follow。第二种情况：$\beta$可以为$varepsilon$，因此可以转换为第一种情况。】

LL(1)分析法

消除左递归、提取最左公因子、构造First集、Follow集

LL(1)分析法的条件

1. 文法不含左递归
2. 每个非终结符A的各个产生式的候选首符集两两不相交
3. 对于每个非终结符A，若它存在某个候选首符集包含$\epsilon$，则$First(A)\cap Follow(A)$=空集

如果一个文法G满足以上条件，则称该文法为LL(1)文法，其中LL代表从左到右扫描输入串、最左推导，1表示每次分析一个输入串的一个符号。

语法分析——自下而上分析

自下而上(Bottom-up)分析法

• 从输入串开始，逐步进行归约，直到文法的开始符号
• 归约:根据文法的产生式规则，把串中出现的产生式的右部替换成左部符号
• 从树叶节点开始，构造语法树
• 算符优先分析法、LR分析法

算符优先分析法：

• 按照算符的优先关系和结合性质进行语法分析
• 适合分析表达式

LR 分析法：

• 规范归约：句柄作为可规约串。

移进规约法

设置一个栈，不断地将输入符号串中的第一个字符移进到符号栈中，一旦栈顶形成某个产生式的右部时，就用该产生式左部的非终结符代替，这个过程称为规约。

短语和直接短语和句柄

令G是一个文法，S是文法的开始符号，假定$\alpha \beta \theta$是文法G的一个句型，如果有

$$S{\Rightarrow }^{\ast }\alpha \beta \theta 且A{\Rightarrow }^{\ast }\beta$$

则称$\beta$是句型$\alpha \beta \theta$的短语（且是相对于非终结符A的）【短语可以进行规约】

如果$\beta$由A一步推出，则为直接短语。【直接短语可以在下一步进行规约】

一个句型的最左直接短语称为该句型的句柄。

规范规约

简而言之，每次只对句柄进行规约。

规范规约是最左规约，他的逆过程是最优推导，因此，最优推导被称为规范推导。

LR分析法

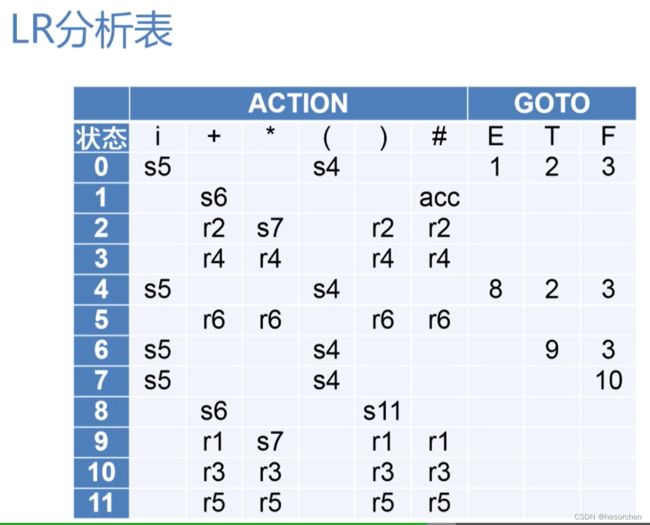
LR分析法先用分析表产生器产生一张LR分析表，LR分析表是LR分析法的核心，有了LR分析表，我们只需自动化的根据输入的单词对照分析表进行分析即可。

在LR分析过程中，我们新增了一个状态栈，每次要加入新的单词时，我们用二元组（状态栈栈顶元素，输入串的首字符）来查找LR分析表。

LR分析表的列表示状态，行表示现在要加入的字符，和上面提到的二元组对应。行分为了两部分：

• Action 表示接受输入串首字符的状态转换。
• GOTO 表示规约的状态转换。

LR分析表中有四种内容：

1. 空白：表示语法错误
2. $sa$：表示将状态a和输入串的首字符压入栈
3. $ra$：表示利用第a条产生式进行规约，将第a条产生式右部及其状态都弹出栈之后，状态转换为（新的状态栈栈顶状态，GOTO中的第a条产生式的左部）
4. $acc$：accept表示接受该句子

LR文法

如果一个文法，能够构造一张分析表，使得他的每个入口均是唯一确定的，则这个文法就称为LR文法。

如果一个文法，能够用一个每步顶多向前检查K个输入符号的LR分析器进行分析，则这个文法称为LR(K)文法。

字的前缀、活前缀

字的前缀：是指字的任意首部，如字$abc$的前缀有$\epsilon$、$a$、$ab$、$abc$

活前缀：是指规范句型的一个前缀，这种前缀不含句柄之后的任何符号。即，对于规范句型$\alpha \beta \theta$，$\beta$为句柄，如果$\alpha \beta =u_1{u}_2{u}_3...u_r$，则符号串$u_1{u}_2...u_i(1\le i\le r)$都是$\alpha \beta \theta$的活前缀。

LR(0)项目

在每个产生式的右部添加一个圆点，圆点左边的部分表示已经接受，右边部分表示期望接受。

$A\to XYZ$有四个项目：

$A\to \cdot XYZ$
$A\to X\cdot YZ$
$A\to XY\cdot Z$
$A\to XYZ\cdot$

$A \rightarrow \alpha · $称为规约项目。
$S \rightarrow \alpha · $称为接受项目，S为文法开始符号。
$A \rightarrow \alpha ·b $称为移进项目。【移进终结符b】
$A \rightarrow \alpha · B $称为待约项目。【等待B规约完成】

构造识别文法所有活前缀的DFA

1. 构造识别文法所有活前缀的NFA
2. 将NFA确定化

这种方法构造识别活前缀的DFA的方法为：写出项目、构造NFA、NFA确定化。工作量大，在此不写过程，建议直接学习下面的方法。

通过构造项目集规范簇来构造识别文法所有活前缀的DFA

项目集的闭包Closure：

• 假定$I$是文法$G$的任一项目集。定义和构造$I$的闭包$Closure(I)$如下：

1. $I$的任何项目都属于$Closure(I)$；
2. 若$A\to \alpha \cdot B\beta$属于$Closure(I)$，那么对于任何关于$B$的产生式$B\to \theta$，都属于$Closure(I)$

把握算法核心：其实和之前NFA的$\epsilon$-闭包定义一样，闭包是经过若干条$\epsilon$弧能到达的其他项目。

项目集的状态转换函数GO：

为了识别活前缀，我们定义一个状态转换函数$GO$。$I$是一个项目集，$X$是一个文法符号。函数值$GO(I,X)$定义为：

$$GO(I,X)=Closure(J)$$

把握算法核心：也和之前NFA的定义$I_X$一样，经过一条$X$弧能到达的其他项目。

算法步骤：

1. 拓广文法，添加产生式$0:S^{\prime }\to S$
2. 写出项目集0，将产生式$0:S^{\prime }\to S$的闭包写入。
3. 计算已有项目集的所有GO函数，拓广项目集。
4. 循环步骤3，直到项目集不再增加。

构造LR(0)分析表

【用人话说】

1. 这是个移进项目，所以LR(0)分析表上指令是移进，且状态栈压入新的项目集编号。
2. 这是个规约项目，所以LR(0)分析表上指令是规约
3. 这是个接受项目（也即文法开始符号作为左部的规约项目）
4. DFA的回溯使用，用图论的话说，相当于建立一条反边？
5. 其余位置都说明语法错误。

然后我们就可以愉快的利用LR(0)分析表分析文法啦~

四元式

这里写出几个常用的四元式

(jnz,a, ,row) // 如果a为真，跳转到第row行
(j>,a,b,row) // 如果a>b，跳转到第row行
(j<,a,b,row) // 如果a

两个重要的框架【有了这俩框架，啥都能写出来】

• $if-else$框架

用a和b中的大值减小值的四元式序列：
if(a > b) T = a - b;
else T = b - a;

1 (j>,a,b,3) //if(a>b)跳转到第3行
2 (j, , ,4) //else 跳转到第5行
3 (-,a,b,T) 
4 (j, , ,6) //退出
5 (-,b,a,T)
6

• $while$框架

当a>0，循环自减的四元式序列：
while(a > 0) a = a - 1;

1 (j>,a,0,3) //while(j>0)跳转到第3行
2 (j, , ,6) //else 退出
3 (-,a,1,T) //T=a-1
4 (=,T, ,a) //a=T
5 (j, , ,1) //跳转回1
6

参考资料

1. 中国大学mooc-国防科技大学-编译原理