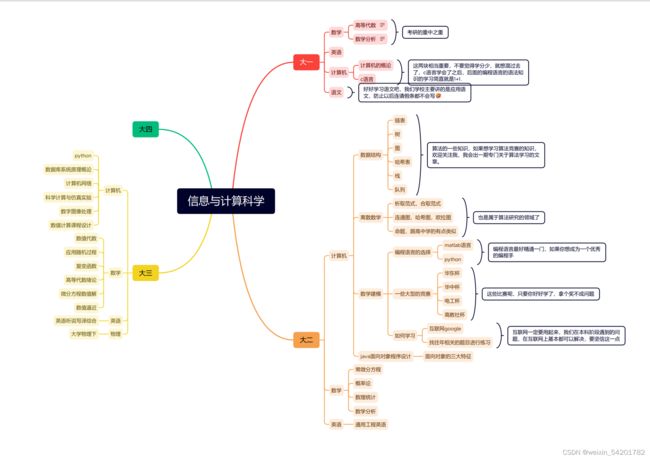
一图帮你了解什么是信息与计算科学专业
本人介绍:双非一本大三混子,有点后悔自己没有在大学一开始就选定自己的方向。侥幸在大学时期获得过校级数模三等奖,校级ACM二等奖,市场调查分析大赛省级二等奖。综合测评班级第一,获得过国家励志奖学金,校级一等奖学金;大一两个学期无脑通关英语四六级,计算机二级。
信息与计算科学学习内容:
在此之前想说的一些话:
(1)选择方向很重要,大学里面空余的时间会很多,一定要不断的去尝试,从而找到自己喜欢研究的领域或者未来想要从事的工作。如果是家中有矿的,当我没说。
(2)大学里面的很多课程都是帮助我们拓宽视野的,比如说数据库系统概论,学校开设这门课程不是为了能够帮助我们找到工作的,而是为了找到自己在研究生方面的研究领域的。找工作和选择升学,就相当于鱼与熊掌不可兼得。
(3)珍惜时间,大学除了学习课程上面的东西,还有很多是值得我们去学习的。不要all in 课程。毕竟大学生活还是很丰富精彩的,学生会的工作,社团的活动在大一的时候还是可以去尝试一下,多多认识优秀的人,更重要的是学习在为人处事上面的方式方法,这一点是终生受益的。
(4)自学能力相当重要。本科期间就是在不断的锻炼你的自学能力的过程。---授人以鱼不如授人以渔。
(5)这里引用以下《肖申克的救赎》里面的一段话“你知道,有些鸟儿注定不会被关在牢笼里的,它们的每一片与羽毛都闪耀着自己的光辉”。
下面是一些大学时期需要学习的内容(思维导图):
因为目前我还是正在读大三,并且大三下的时候我打算去实习,所以在大三和大四的部分就有点儿省略了,后期到我大四的时候我会去修改的。
数学:高等代数、数学分析、常微分方程、概率论、数理统计、应用随机过程、离散数学,运筹学。计算机:c语言、matlab、python、java面向对象、数据结构、计算机网络、数据库系统概论、离散数学(这个有点计算机的意思)英语学习:通用工程英语视听说、通用工程英语读写。语文:大学应用语文。
英语四六级:正常情况下能够在大一的时候通过,就努把力通过,到了后面你不要指望每周一次的英语课就可以带你英语突飞猛进。很多人大一没有通过,后面就真的不会过了。
计算机二级:这个东西我当时c语言也是没学完,就去报了一个计算机二级的证,还优秀通过了,说真的,这个证在计算机专业来说就真没啥含金量。我大一的时候学习能力贼差劲,基本的word文档如何自动生成目录都不会的那种,都可以用差不多一个月的时间通过,所以你也一定可以的。
一些课程的介绍:
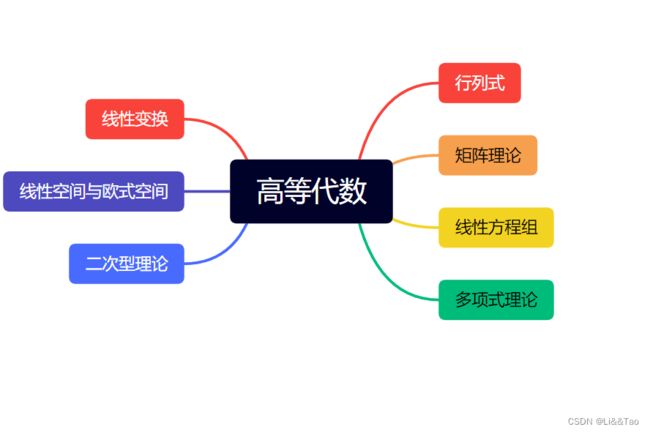
(1)高等代数:这里先引用以下官方的解释
初等代数从最简单的一元一次方程开始,初等代数一方面进而讨论二元及三元的一次方程组,另一方面研究二次以上及可以转化为二次的方程组。沿着这两个方向继续发展,代数在讨论任意多个未知数的一次方程组,也叫线性方程组的同时还研究次数更高的一元方程组。发展到这个阶段,就叫做高等代数。高等代数是代数学发展到高级阶段的总称,它包括许多分支。现在大学里开设的高等代数,一般包括两部分:线性代数、多项式代数。
(2)数学分析:数学分析 (英语: mathematical analysis )区别于其他非数学类学生的 高等数学 内容,是分析学中最古老、最基本的分支,一般指以 微积分学 、 无穷级数 和 解析函数 等的一般理论为主要内容,并包括它们的理论基础( 实数 、 函数 、 测度 和 极限 的基本理论)的一个较为完整的数学学科。. 它也是大学数学专业的一门基础课程。. 数学分析研究的内容包括 实数 、 复数 、实函数及复变函数。. 数学分析是由微积分演进而来,在微积分发展至现代阶段中,从应用中的方法总结升华为一类综合性分析方法,且初等微积分中也包括许多数学分析的基础概念及技巧,可以认为这些应用方法是高等微积分生成的前提。. 数学分析的方式和其几何有关,不过只要任一数学空间有定义邻域( 拓扑空间 ...)
个人学习的感受:数学分析和高等代数是大学的数学,不像高中的数学知识,尤其是数学分析,从一开始学极限的时候,你就会感受到它不是运用数学知识的,而是不断的证明数学知识,根据一个又一个的定理来证明数学定理的。高等代数就有点类似于不断的再教你一些高级的运算技巧,具体的比如矩阵的行列式的计算技巧,行列式运算的一些性质,除此之外高等代数也有很多的证明题目,但是不是像复旦大学这种数学学习氛围极强的高校的话,不会去考大量的证明题目的,毕竟高等代数的很多的计算问题涉及道的知识点有很多很多,单纯的计算能力和记忆能力就会刷掉很多人了。一个数字没有计算对,就会导致整个行列式的错误,毕竟大学的数学,是要学会计算精确的值的,大学要开设数学课程的目的是为了培养出一个有一个对数学感兴趣,喜欢研究数学严谨性的人才的。
本人成绩的话每个学期学的高等代数和数学分析平均起来也有个85分了,我们学院里面还是有很多的大佬,平均分都能拿90分的,所以相比之下我好像是个菜鸡。
想给大一新生的一些建议:数学分析和高等代数的学习都不会是一帆风顺的,这是学习过程中必须要接受的现实。如果你连这点困难都克服不了的话,我劝你还是不要去研究一些研究生接触到的数学了,至于大学的计算机的话:最难熬的便是c语言程序设计,c语言的指针,结构体,函数,文件操作,这些东西一定要搞清楚。学习编程就必须要实验,对我就是当时没有多多实验,而是选择一个看书的办法去学习编程的,并且编程的时候也是照抄别人写的代码,现在才知道当时如果编程的时候多自己实现以下,自己可能就拿到ACM的大奖了。你现在遇到的问题,遇到一个就去解决一个,这样你才会不断进步。如果你是想着期末飘过的话,那么选择去问问学长有没有计算机期末编程的题目,这样子背一背答案就可以过了。
想给大二学弟学妹的一些建议:学好数据结构和离散数学,java面向对象程序设计。对于以后参加数模竞赛,ACM竞赛都会有帮助的。因为数据结构如果你考研的话,选择的是计算机方向的,那么数据结构是必考的。如果你是打算找工作的话,学习数据结构主要是学一些算法,学习这些常用的数据结构去解决一些算法的问题。所以我强烈推荐学好数据结构。 都说大一打基础,大二干嘛?大二打比赛啊!哈哈,我认为一点都没有错。
算法学习过程中会遇到的问题:
1.我写这个算法题目写了一个小时了,还是没有一点思路怎么办?
没有思路,一个小时了,如果你是一直在不断的思考,想了一个小时了,还是没有相处来,那么我建议你可以去看相关的题解,一定会有收获的,看完之后,最忌讳的事情就是去做cv操作,不要这样子,因为这个算法不是你实现的,你需要理解它的思路,然后从零开始构建的去学习,去编程,不要去记忆你要参考的代码。这个过程中你会发现自己的脑阔异常的疼,但进步也会立马就来了,你只有这么不断的去训练,不断的积累,坚持,我相信你一定可以拿下ACM奖牌的。
2.算法知识这么多,我这么会学的玩呢?
一定要有一个长远的目标,即我要达到什么样的目标,我要在什么时候拿到什么奖,然后就是去不断的执行和调整就很好了。
3.每次打比赛总是排名很靠后,没有信心?
别人比你付出了很多的时间和精力,凭什么比你要差呢?你所要做的就是不断的提升自己的水平,现在的算法能力没有它强,那么我一年之后后,我坚持每天写个2道算法题目,坚持一年之后,再看看,你已经把别人甩的很远了。所以一定要有长远的眼光。现在是不是觉得高中的政治有用了。
一些重要的比赛:
(1)程序设计类的:
ACM程序设计大赛、蓝桥杯(涉及的算法知识很多)
算法学习的平台:
个人推荐牛客网上面有一个新手入门题单,我刷了有200多道题目吧,感觉里面的题目加上在线的oj平台非常适合我这种类型的选手,强烈不建议到杭电OJ去刷题,这个网站延迟会很大,一个程序提交之后,会很卡。(这里强烈推荐牛客OJ和洛谷的OJ)
牛客网的训练网址:https://ac.nowcoder.com/discuss/817596?f=b
洛谷网站:首页 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
对算法学习感兴趣的,我会在专栏中不断更新自己在学习算法过程中走过的心路,帮助更多的朋友少走点弯路。
算法的学习是一个持续的过程,需要每日坚持刷题来增强手感。刚入门你会发现你有很多的程序都时写不出来的,刚开始的时候,我连最基本的判断一个数是不是素数我都不会写,一个return 1;到底时什么都不知道。后面随着你编程经验的积累,你会发现这些不会写的逐渐都会写了。再接着之后,你学会了一些基本的循环语句,条件语句,掌握一些简单的数论,高精度的一些知识,可以去参加牛客网每周举办的小白周赛,很多大佬就产自于周赛。[手动狗头]。如果你真的特别喜欢算法竞赛,不满足于在学校里面拿个奖,那么参加到学校的ACM协会将会是一个不错的选择,祝你成功。
(2)数学建模:
数学建模大赛,每个学校举办的流程都不一样,会参加的比赛也都不一样,但是获奖率会很高,然而这有一个条件就是:大一时你的编程能力需要达到一定的水平,比如说用一个matlab绘制出一个爱心,用c语言编程出一个贪吃蛇的程序....
一些可以找到优秀论文的网址:数学建模论文 - 中国大学生在线
最后想说的:
学习是一个终生的过程,我们每一天都要在学习,不论是在课堂上面,还是在以后的工作生活中。然后希望每个想我一样焦虑的同学,都能有一个充实的大学生活,每天把自己的生活安排好,不去担心哪些不确定的未来,活在当下,去学习,去感悟,四年后你一定会遇到一个不一样的自己。Make some actual use of your life.希望看到这篇文章的你,哪怕对你只有一点点的帮助,也许是某一段的几个文字给你带来了不一样的体验,让你的大学生活过的丰富且精彩。这就是我在不断创作的动力了。
最后还是引用一下肖申克救赎里面的一段话:“你知道,有些鸟儿注定不会被关在牢笼里的,它们的每一片与羽毛都闪耀着自己的光辉”。本文只是对我所学的专业的大致的一个概述,如果有大佬不喜欢,或者我有哪些不对的地方都可以在评论区下方留言。
文献引用:
数学分析的概念:https://zh.wikipedia.org/
高等代数的概念:高等代数(数学课程)_百度百科