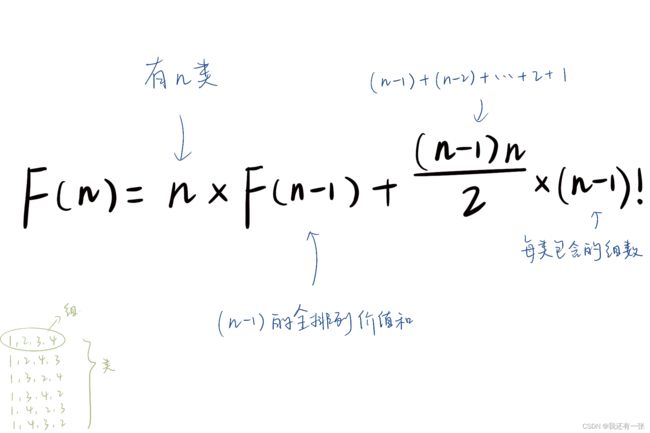蓝桥杯2022年第十三届省赛真题-全排列的价值
题目描述
对于一个排列 A = (a1, a2, · · · , an),定义价值 ci 为 a1 至 ai−1 中小于 ai 的数的个数,即 bi = |{aj | j < i, aj < ai}|。定义 A 的价值为
![]()
给定 n,求 1 至 n 的全排列中所有排列的价值之和。
输入格式
输入一行包含一个整数 n 。
输出格式
输出一行包含一个整数表示答案,由于所有排列的价值之和可能很大,请输出这个数除以 998244353 的余数。
样例输入
3
样例输出
9
提示
1 至 3 构成的所有排列的价值如下:
(1, 2, 3) : 0 + 1 + 2 = 3 ;
(1, 3, 2) : 0 + 1 + 1 = 2 ;
(2, 1, 3) : 0 + 0 + 2 = 2 ;
(2, 3, 1) : 0 + 1 + 0 = 1 ;
(3, 1, 2) : 0 + 0 + 1 = 1 ;
(3, 2, 1) : 0 + 0 + 0 = 0 ;
故总和为 3 + 2 + 2 + 1 + 1 = 9。
对于 40% 的评测用例,n ≤ 20 ;
对于 70% 的评测用例,n ≤ 5000 ;
对于所有评测用例,2 ≤ n ≤ 106 。
解决思路
刚开始拿到这个题目没什么思路,就拿手写了一下。
n=2时,
(1, 2) : 0 + 1 = 1;
(2, 1) : 0 + 0 = 0;
故总和为1 + 0 = 1。
n=3时,
(1, 2, 3) : 0 + 1 + 2 = 3 ;
(1, 3, 2) : 0 + 1 + 1 = 2 ;
(2, 1, 3) : 0 + 0 + 2 = 2 ;
(2, 3, 1) : 0 + 1 + 0 = 1 ;
(3, 1, 2) : 0 + 0 + 1 = 1 ;
(3, 2, 1) : 0 + 0 + 0 = 0 ;
故总和为 3 + 2 + 2 + 1 + 1 = 9。
n=4时,
(1, 2, 3, 4) : 0 + 1 + 2 + 3 = 6 ;
(1, 2, 4, 3) : 0 + 1 + 2 + 2 = 5 ;
(1, 3, 2, 4) : 0 + 1 + 1 + 3 = 5 ;
(1, 3, 4, 2) : 0 + 1 + 2 + 1 = 4 ;
(1, 4, 2, 3) : 0 + 1 + 1 + 2 = 4 ;
(1, 4, 3, 2) : 0 + 1 + 1 + 1 = 3 ;
... ...
(4, 1, 2, 3) : 0 + 0 + 1 + 2 = 3 ;
(4, 1, 3, 2) : 0 + 0 + 1 + 1 = 2 ;
(4, 2, 1, 3) : 0 + 0 + 0 + 2 = 2 ;
(4, 2, 3, 1) : 0 + 0 + 1 + 0 = 1 ;
(4, 3, 1, 2) : 0 + 0 + 0 + 1 = 1 ;
(4, 3, 2, 1) : 0 + 0 + 0 + 0 = 0 ;
故总和为72。
不妨可以自己列一下试试看……
在当我列到(4,1,2,3)时,我突然意识到,以4开头的这6组排列的价值和,不正和n=3时的价值和一模一样吗?都是3+2+2+1+1+0=9。
所以固定一个数在首位,后面的剩余的3个数的全排列价值和,正是n=3时的全排列价值和。这时只需要再考虑,后三位与首位之间的大小关系即可。
以1开头的6组为例,4>3>2>1,后三位均大于首位,所以每一组的价值都要再加3,所以以1开头的6组价值和为(3+3)+(2+3)+(2+3)+(1+3)+(1+3)+(0+3)=27。
同理,以2开头的6组,由于4>3>2,后三位中只有2位大于首位,所以每一组的价值都要再加2,所以以2开头的6组价值和为(3+2)+(2+2)+(2+2)+(1+2)+(1+2)+(0+2)=21。
同理,以3开头的6组,由于只有4>3,所以每一组的价值都要再加1,所以以3开头的6组价值和为(3+1)+(2+1)+(2+1)+(1+1)+(1+1)+(0+1)=15。
同理,以4开头的6组,后三位中没有数大于首位,所以直接就是(3+0)+(2+0)+(2+0)+(1+0)+(1+0)+(0+0)=9。
我们把以1开头、以2开头、以3开头、以4开头这样的设为一大类。
设全排列的价值和为F(n),这样就可以推导出F(n)和F(n-1)的关系式了。
不妨可以用n=3和n=2时的情况来验证下。
代码
# 符合题目逻辑的代码
N = int(input())
F = 1
G = 1
for n in range(3,N+1):
p1 = n*F
G = G*(n-1)
T = (n-1)*n/2
p2 = G*T
F = (p1+p2)
print(int(F%998244353))
问题
仅仅像上面这么写肯定是不行的,因为数字很大会超出范围,所以要提前就对公式的每一部分做除余操作,于是我又写了
# 符合题目要求的代码
N = int(input())
F = 1
G = 1
for n in range(3,N+1):
p1 = (n*F) %998244353
G = (G*(n-1)) %998244353
T = ((n-1)*n/2) %998244353
p2 = (G*T) %998244353
F = (p1+p2) %998244353
print(int(F))但是通过率只有59%,当数字变大到21的时候,代码段2和代码段1的结果就不一样了,想了半天都不知道问题出在哪,求大佬帮助。