leetCode 2915. 和为目标值的最长子序列的长度 + 动态规划 +01背包 + 空间优化 + 记忆化搜索 + 递推

2915. 和为目标值的最长子序列的长度 - 力扣（LeetCode）

---

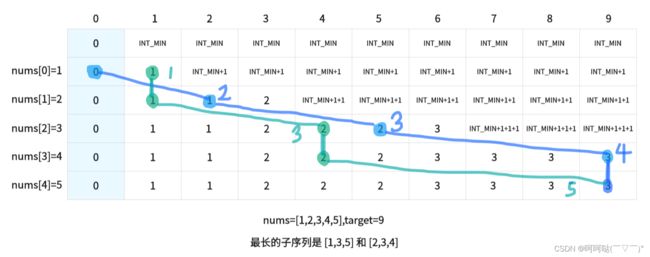
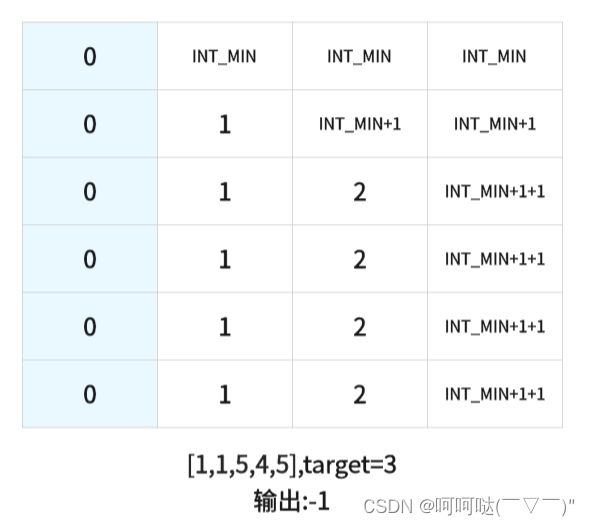
给你一个下标从 0 开始的整数数组 nums 和一个整数 target 。返回和为 target 的 nums 子序列中，子序列 长度的最大值 。如果不存在和为 target 的子序列，返回 -1 。子序列 指的是从原数组中删除一些或者不删除任何元素后，剩余元素保持原来的顺序构成的数组。

（一）回溯 

• f(i,j) 表示在物品集 nums 的前 i 个选取物品，使得装满容量为 j 的背包有最多个物品
• 也就是f(i,j) 表示在数组 nums 的前 i 个的选取元素，使得这些元素之和等于 j 的 最长子序列长度
• 

class Solution {
public:
    // 递归搜索
    int lengthOfLongestSubsequence(vector& nums, int target) {
        int n = nums.size();
        functiondfs=[&](int i,int s) -> int {
            if(i<0) { 
                if(s==0) return 0;
                else return INT_MIN;
            }
            return max(dfs(i-1,s),dfs(i-1,s-nums[i])+1);
        };
        int ans = dfs(n-1,target);
        return ans<0?-1:ans;
    }
};

（二） 递归搜索 + 保存计算结果 = 记忆化搜索

class Solution {
public:
    // 记忆化递归搜索
    int lengthOfLongestSubsequence(vector& nums, int target) {
        int n = nums.size();
        vector> memo(n,vector(target+1,-1));
        functiondfs=[&](int i,int s) -> int {
            if(i<0) { 
                if(s==0) return 0;
                else return INT_MIN;
            }
            int& res = memo[i][s];
            if(res != -1) return res;
            if (s < nums[i]) return res = dfs(i-1,s);
            return res = max(dfs(i-1,s),dfs(i-1,s-nums[i])+1);
        };
        int ans = dfs(n-1,target);
        return ans<0?-1:ans;
    }
};

class Solution {
public:
    // 记忆化递归搜索
    int lengthOfLongestSubsequence(vector& nums, int target) {
        int n = nums.size();
        vector> memo(n+1,vector(target+1,-1));
        functiondfs=[&](int i,int s) -> int {
            if(i<0) { 
                if(s==0) return 0;
                else return INT_MIN;
            }
            int& res = memo[i+1][s];
            if(res != -1) return res;

            // 不选
            int& x = memo[i][s];
            if(x == -1) x=dfs(i-1,s);
            if (s < nums[i]) return res=x;

            // 选
            int& y = memo[i][s-nums[i]];
            if(y == -1) y=dfs(i-1,s-nums[i]);
            return res = max(x,y+1);
        };
        int ans = dfs(n-1,target);
        return ans<0?-1:ans;
    }
};

（三）1:1 翻译成递推

• 
• 
• 

class Solution {
public:
    // 递推
    int lengthOfLongestSubsequence(vector& nums, int target) {
        int n = nums.size();
        vector> f(n+1,vector(target+1,INT_MIN));
        f[0][0]=0;
        for(int i=0;i=nums[i]) f[i+1][j] = max(f[i][j],f[i][j-nums[i]]+1);
                // else f[i+1][j] = f[i][j];
                f[i+1][j] = f[i][j];
                if(j>=nums[i]) f[i+1][j] = max(f[i][j],f[i][j-nums[i]]+1);
            }
        }
        int ans = f[n][target];
        return ans<0?-1:ans;
    }
};

进一步优化:

class Solution {
public: 
    // 递推 + 优化
    int lengthOfLongestSubsequence(vector& nums, int target) {
        int n = nums.size();
        vector> f(n+1,vector(target+1,INT_MIN));
        int sum=0;
        for(int i=0;i=nums[i]) f[i+1][j] = max(f[i][j],f[i][j-nums[i]]+1);
            }
        }
        int ans = f[n][target];
        return ans<0?-1:ans;
    }
};

>>空间优化

• 1、二维数组空间优化

class Solution {
public:
    // 二维空间优化
    int lengthOfLongestSubsequence(vector& nums, int target) {
        int n = nums.size();
        vector> dp(2,vector(target+1,INT_MIN));
        int sum=0;
        for(int i=0;i= nums[i]) dp[(i+1)%2][j] = max(dp[i%2][j],dp[i%2][j-nums[i]]+1);
                else dp[(i+1)%2][j] = dp[i%2][j];
            }
        }
        int ans = dp[n%2][target];
        return ans<0?-1:ans;
    }
};

• 2.一维空间优化

class Solution {
public:
    // 一维空间优化
    int lengthOfLongestSubsequence(vector& nums, int target) {
        int n = nums.size();
        vector dp(target+1,INT_MIN);
        dp[0]=0;
        int sum=0;
        for(int i=0;i=nums[i];j--) {
                dp[j] = max(dp[j],dp[j-nums[i]]+1);
            }
        }
        int ans = dp[target];
        return ans<0?-1:ans;
    }
};

内容总结来自B站这位up主（Horn_JoJo）的视频简介：（总结得超棒！！！）

动态规划之选或者不选 通过「选」或「不选」，确定子问题与原问题的联系。子问题又可以通过同样的「选」或者「不选」来再次找到子子问题与子问题的联系。这样就可以不断将问题拆成子问题。就构成了一个搜索树。当拆分到一定程度时，则找到了最容易解决的子问题。这样就可以先将子问题解决掉，然后反过来解决较大的子问题。这样就可以解决原问题了。

• 树的根结点时原问题。树的叶子结点是边界或者最小子问题。
• 自顶向下：直接递归(满二叉树本，有重复子问题)， 记忆化搜索(递归+记录)减少重复计算。
• 自底向上：省略「递」的过程，直接「归」的过程中计算。

推荐和参考文章、视频： 

116双周赛T3复盘_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1Zg4y197BR/?spm_id_from=333.788.top_right_bar_window_history.content.click&vd_source=a934d7fc6f47698a29dac90a922ba5a3

动态规划入门：从记忆化搜索到递推_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1Xj411K7oF/?spm_id_from=333.788&vd_source=a934d7fc6f47698a29dac90a922ba5a3

2915. 和为目标值的最长子序列的长度 - 力扣（LeetCode）https://leetcode.cn/problems/length-of-the-longest-subsequence-that-sums-to-target/solutions/2502839/mo-ban-qia-hao-zhuang-man-xing-0-1-bei-b-0nca/我的往期文章：

leetCode 198.打家劫舍 动态规划入门:从记忆化搜索到递推-CSDN博客https://blog.csdn.net/weixin_41987016/article/details/134179583?spm=1001.2014.3001.5501