算法通关村第六关-白银挑战树

大家好我是苏麟 , 今天聊聊树 .

树的概念

树是我们计算机中非常重要的一种数据结构，同时使用树这种数据结构，可以描述现实生活中的很多事物，例如家谱、单位的组织架构、等等。
树是由n（n>=1）个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

更好的理解 :

如企业里的职级关系 :

如一本书的目录 :

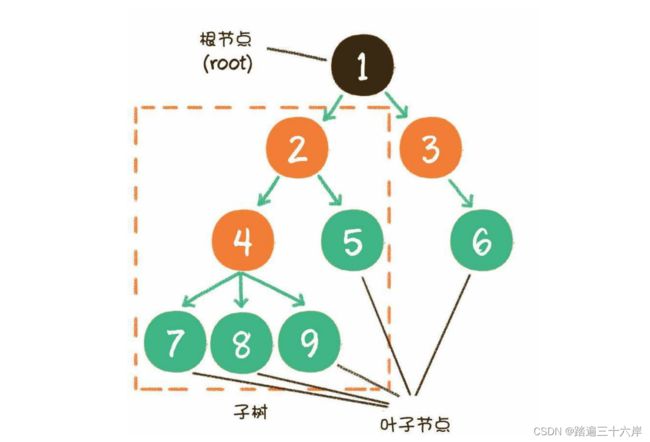
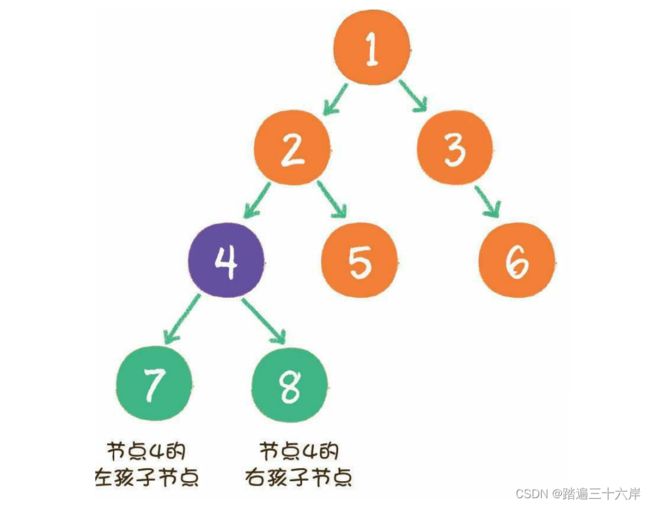
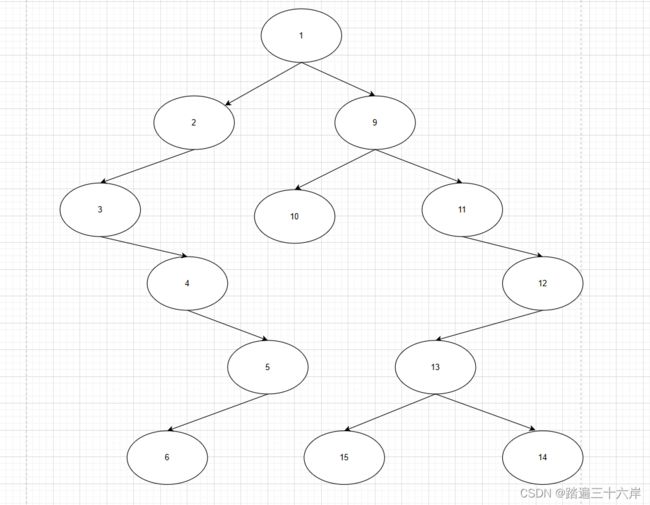
下面这张图，就是一个标准的树结构 :

树具有以下特点：

1.每个结点有零个或多个子结点
2.没有父结点的结点为根结点
3.每一个非根结点只有一个父结点
4.每个结点及其后代结点整体上可以看做是一棵树，称为当前结点的父结点的一个子树

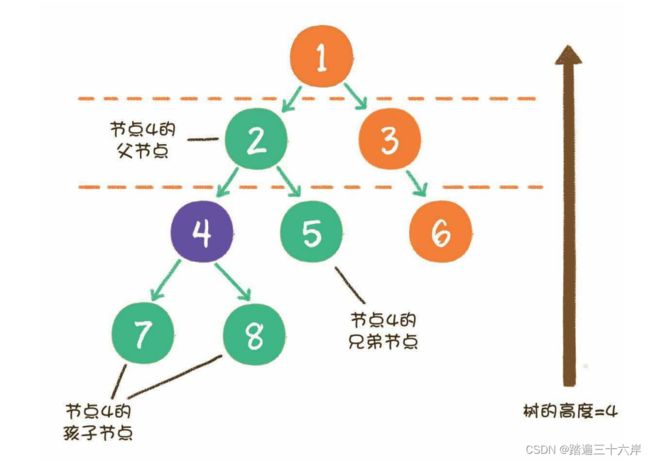
参考上面的结构，可以很方便的理解树的如下概念:

1.节点的度:一个节点含有的子节点的个数称为该节点的度
2.树的度:一棵树中，最大的节点的度称为树的度，注意与节点度的区别
3.叶节点或终端节点: 度为0的节点称为叶节点
4.非终端节点或分支节点:度不为0的节点
5.双亲节点或父节点:若一个节点含有子节点，则这个节点称为其子节点的父节点
6.孩子节点或子节点: 一个节点含有的子树的根节点称为该节点的子节点
7.兄弟节点: 具有相同父节点的节点互称为兄弟节点
8.节点的祖先: 从根到该节点所经分支上的所有节点
9.子孙: 以某节点为根的子树中任一节点都称为该节点的子孙
10.森林: 由m(m>=0)棵互不相交的树的集合称为森林
11.无序树:树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树
12.有序树:树中任意节点的子节点之间有顺序关系，这种树称为有序树
13.二又树:每个节点最多含有两个子树的树称为二叉树

二叉树

二叉树（binary tree）是树的一种特殊形式。二叉，顾名思义，这种树的每个节点最多有2个孩子节点。注意，这里是最多有2个，也可能只有1个，或者没有孩子节点。

二叉树的结构如图所示 :

二叉树节点的两个孩子节点，一个被称为左孩子（left child），一个被称为右孩子（right child）。这两个孩子节点的顺序是固定的，就像人的左手就是左手，右手就是右手，不能够颠倒或混淆。

此外，二叉树还有两种特殊形式，一个叫作满二叉树，另一个叫作完全二叉树。

满二叉树

一个二叉树的所有非叶子节点都存在左右孩子，并且所有叶子节点都在同一层级上，那么这个树就是满二叉树。

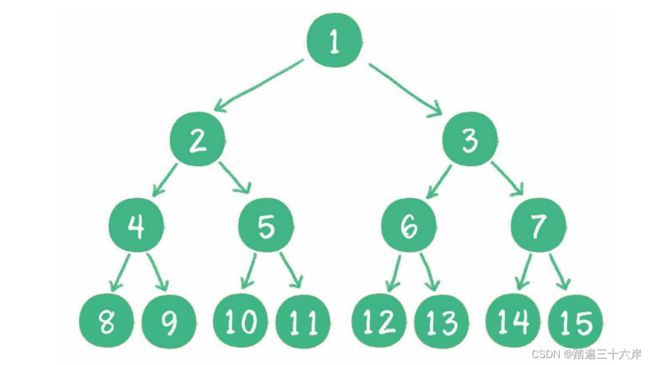
简单点说，满二叉树的每一个分支都是满的。

完全二叉树

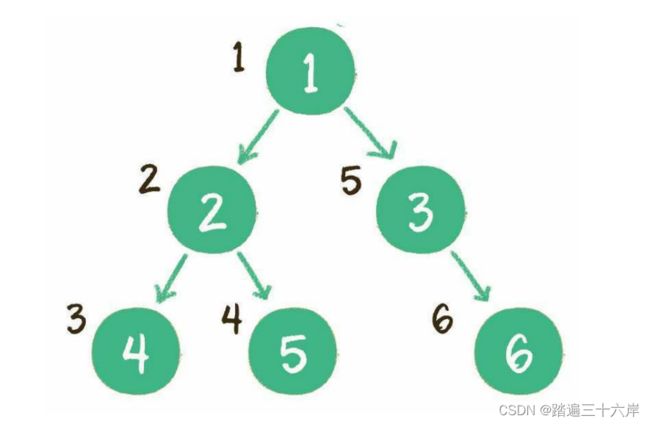
对一个有n个节点的二叉树，按层级顺序编号，则所有节点的编号为从1到n。如果这个树所有节点和同样深度的满二叉树的编号为从1到n的节点位置相同，则这个二叉树为完全二叉树。

如图 :

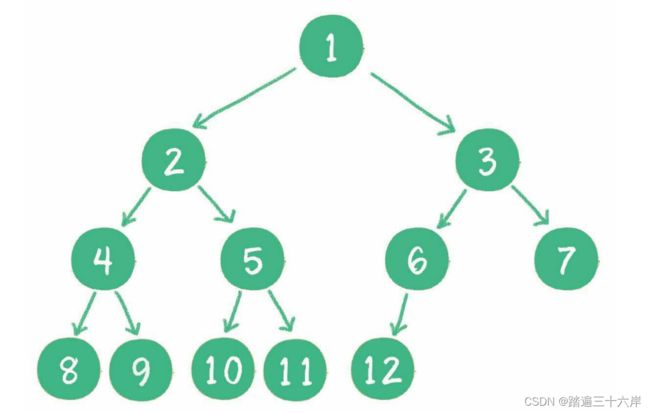
在上图中，二叉树编号从1到12的12个节点，和前面满二叉树编号从1到12的节点位置完全对应。因此这个树是完全二叉树。

完全二叉树的条件没有满二叉树那么苛刻：满二叉树要求所有分支都是满的；
而完全二叉树只需保证最后一个节点之前的节点都齐全即可。

树的性质

性质1: 在二又树的第i层上至多有2^(i-1)个结点 (i>0)
性质2: 深度为k的二又树至多有2^k - 1个结点 (k>0)
性质3: 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则NO=N2+1:
性质4:具有n个结点的完全二叉树的深度必为 log2(n+1)
性质5:对完全二又树，若从上至下、从左至右编号，则编号为i 的结点，其左孩子编号必为2i.
其右孩了编号必为2i+1;其双亲的编号必为i/2 (i= 1 时为根,除外)满二又树和完全二叉树是经常晕的问题，我们有必要单独看一下。满二又树就是如果一棵二叉树只有度为0的节点和度为2的节点，并且度为0的节点在同一层上，则这棵二又树为满二叉树。

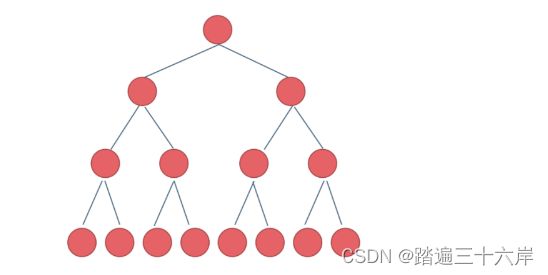
这棵二又树为满二又树，也可以说深度为k=4，有2^k-1=15个节点的二又树。完全二叉树的定义如下:在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大 值并且最下面一层的节点都集中在该层最左边的若千位置这个定义最邪乎了，估计大部分看了之后还是不懂什么是完全二叉树，看这个图就知道了:

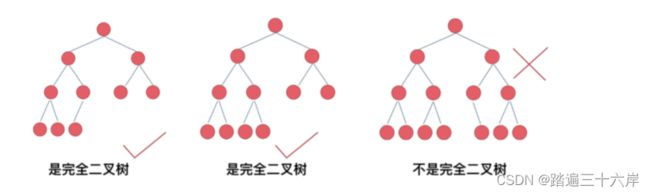
前面两棵树的前n-1层都是满的，最后一层所有节点都集中在左侧区域，而且节点之间不能有空隙。最后个为什么不是?因为有一节点缺了一个左子节点。

树的定义与存储方式

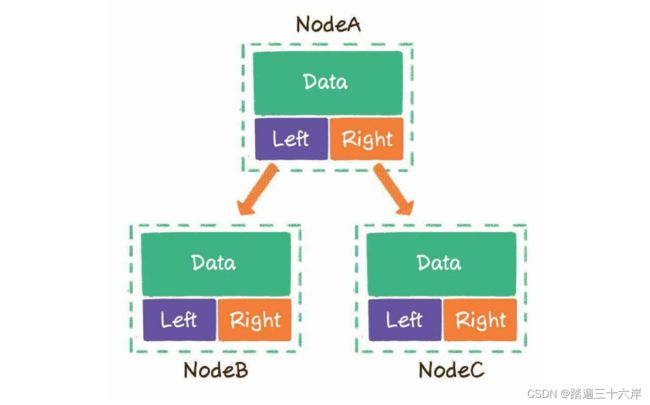
定义二叉树 : 一个节点最多可以指向左右两个孩子节点，所以二叉树的每一个节点包含3部分。

• 存储数据的data变量
• 指向左孩子的left指针
• 指向右孩子的right指针

public class Node{
	int value;
	Node left;
	Node right;
}

链式存储结构

数组存储

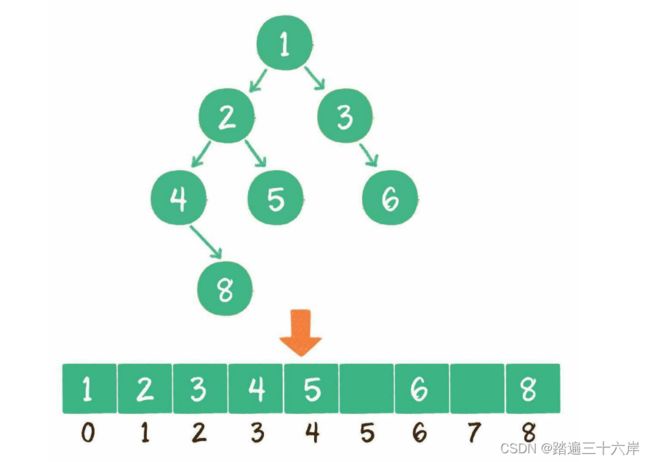
使用数组存储时，会按照层级顺序把二叉树的节点放到数组中对应的位置上。如果某一个节点的左孩子或右孩子空缺，则数组的相应位置也空出来。

对于一个稀疏的二叉树来说，用数组表示法是非常浪费空间的。

树的遍历

二叉树的遍历分为4种 :

1. 前序遍历
2. 中序遍历
3. 后序遍历
4. 层序遍历

从更宏观的角度来看，二叉树的遍历归结为两大类 :

1. 深度优先遍历（前序遍历、中序遍历、后序遍历）

2. 广度优先遍历（层序遍历）

这两种遍历方式不仅仅是二叉树，N叉树也有这两种方式的，图结构也有，只不过我们更习惯叫广度优先和深度优先，本质是一回事。深度优先又有前中后序三种，有同学总分不清这三个顺序，问题就在不清楚这里前中后是相对谁来说的。记住一点:前指的是中间的父节点在遍历中的顺序，只要大家记住 前中后席指的就是中间节点的位置就可以了。

二叉树的前序遍历，输出顺序是根节点、左子树、右子树。

二叉树的中序遍历，输出顺序是左子树、根节点、右子树。

二叉树的后序遍历，输出顺序是左子树、右子树、根节点。

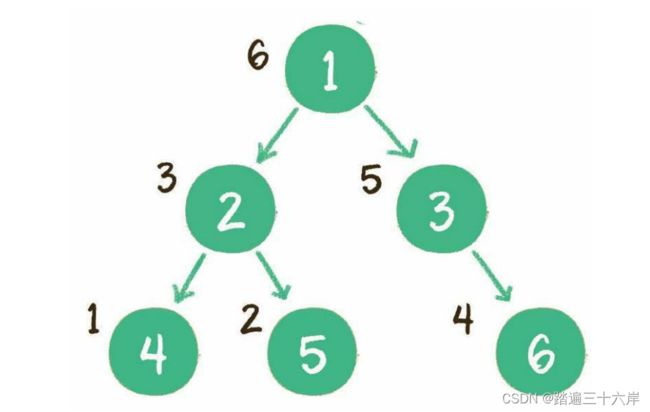
后面大量的算法都与这四种遍历方式有关，有的题目根据处理角度不同，可以用层次遍历，也可以用一种甚至两种深度优先的方式来实现。

通过序列构造二叉树

前面我们已经介绍了前中后序遍历的基本过程，现在我们看一下如何通过给出的序列来恢复原始二叉树看三个序列:

(1)前序: 1 2 3 4 5 6 8 7 9 10 11 12 13 15 14
(2)中序: 3 4 8 6 7 5 2 1 10 9 11 15 13 14 12
(3) 后序: 8 7 6 5 4 3 2 10 15 14 13 12 11 9 1

前中序列遍历

我们先看如何通过前中序列复原二叉树

(1)前序: 1 2 3 4 5 6 8 7 9 10 11 12 13 15 14
(2) 中序: 3 4 8 6 7 5 2 1 10 9 11 15 13 14 12

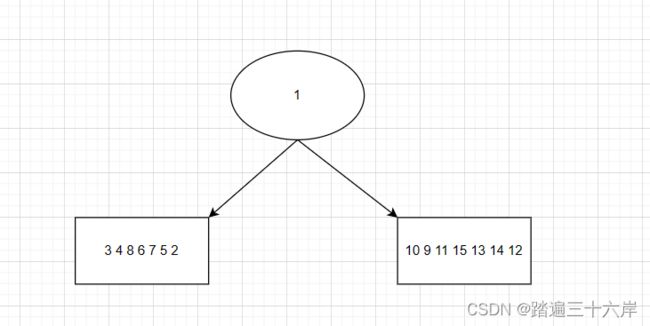
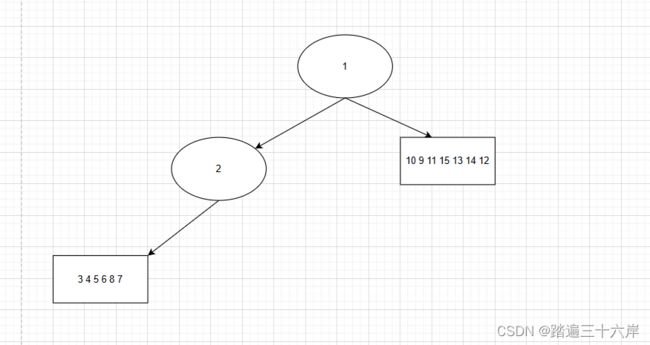
我们知道前序第一个访问的就是根节点，所以根节点就是1。中序遍历的特点是根节点的左子树的元素都在根节点的左侧，右子树的元素都在根节点的右侧，从中序遍历序列我们可以划分成如下结构:

中序序列划分:
[3 4 8 6 7 5 2] 1[ 10 9 11 15 13 14 12]
前序序列划分为:
1 [2 3 4 5 6 8 7 ] [9 1 11 12 13 15 14]

上面前序席列第一个括号里的都是左子树的元素，第二个括号一定都是右子树的元素那这里怎么知道两个括号从哪里分开呢? 是参照中序的两个数组划分的。我们看到前序中7之前的元素都在中序第一个数组中，9之后的所有元素就在第二个数组种，所以我们从7和9之间划分。由此，画图表示一下此时知道的树的结构为:

我们先看两个序列的第一个数组:
前序: 2 3 4 5 6 8 7
中序: 3 4 8 6 7 5 2
此时又可以利用上面的结论划分了: 根节点是2，然后根据2在中序中的位置可以划分为:

前序: 2 [3 4 5 6 8 7 ]
中序: [3 4 8 6 7 5 ]2

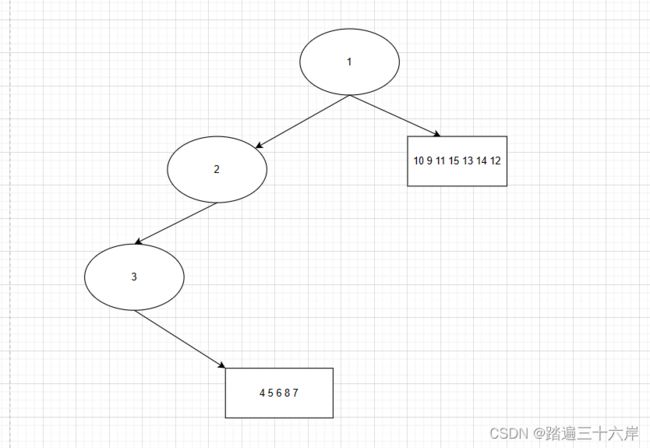
对 3 4 5 6 8 7 继续划分:

前序: 3 [4 5 6 8 7]
中序: 3 [4 8 6 7 5]

此时结构为:

对 4 5 6 8 7 继续划分:

前序: 4 [5 6 8 7]
中序: 4 [8 6 7 5]

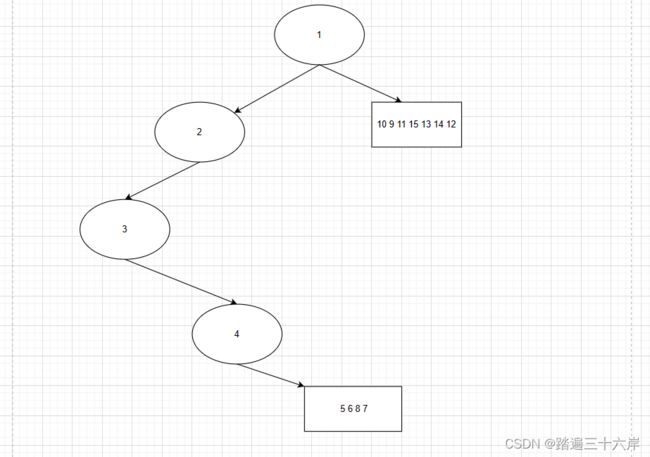
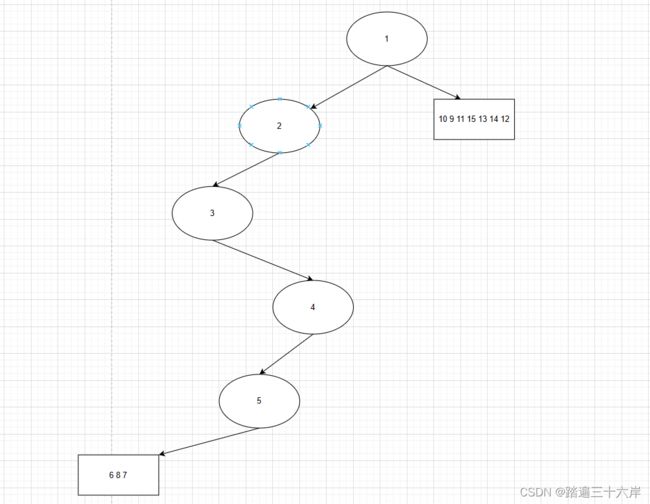
对 5 6 8 7 继续划分:
前序: 5 [6 8 7]
中序: [8 6 7] 5

对 6 8 7 继续划分:
前序: 6 [8 7]
中序: [8 ]6 [7]

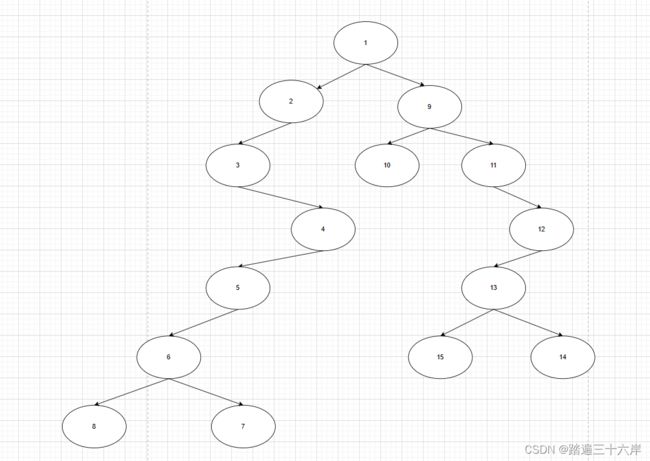
右边也是一样的 , 大家自己动手试试看 …
直接给出最终版本 :

中后序列遍历

我们先看如何通过前中序列复原二叉树

(2)中序: 3 4 8 6 7 5 2 1 10 9 11 15 13 14 12
(3) 后序: 8 7 6 5 4 3 2 10 15 14 13 12 11 9 1

• 第一轮

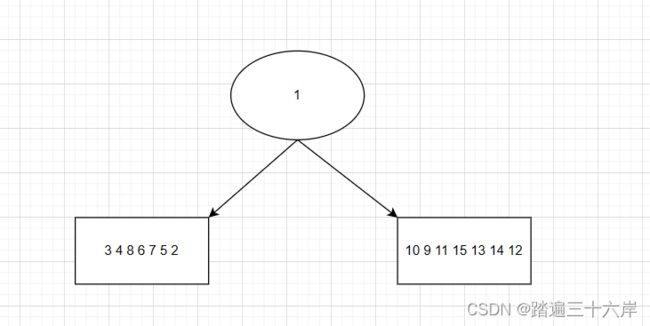
我们知道后序最后一个访问的就是根节点，所以根节点就是1.

中序遍历的特点是根节点的左子树的元素都在根节点的左侧，右子树的元素都在根节点的右侧，从中序遍历序列我们可以划分成如下结构:

中序划分
[3 4 8 6 7 5 2] 1 [10 9 11 15 13 14 12]
后序划分
[8 7 6 5 4 3 2] [10 15 14 13 12 11 9] 1

上面后序序列第一个括号里的都是左子树的元素，第二个括号一定都是右子树的元素.

那这里怎么知道两个括号从哪里分开呢? 是参照中序的两个数组划分的。我们看到前序中7之前的元素都在中序第一个数组中，9之后的所有元素就在第二个数组种，所以我们从7和9之间划分。

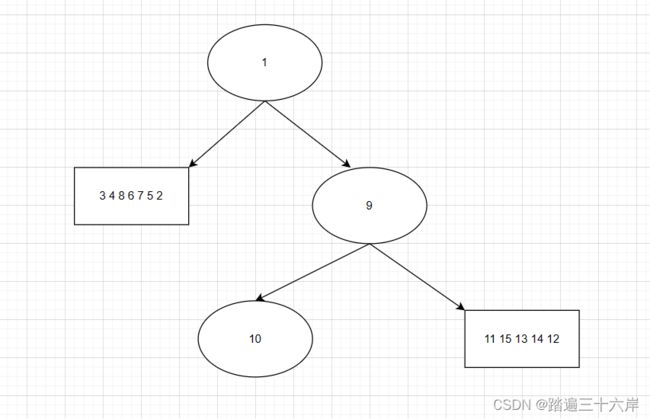
• 第二轮

中序 : [10 9 11 15 13 14 12]
后序 : [10 15 14 13 12 11 9]

此时划分 :

[10 ] 9 [11 15 13 14 12]
[10 15 14 13 12 11 ] 9

此时树的结构 :

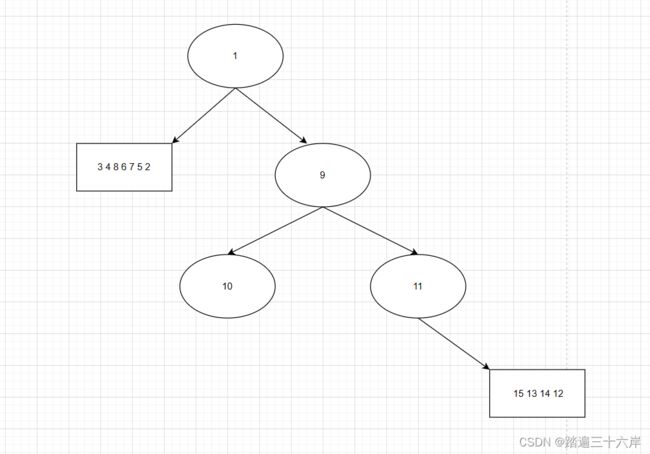
• 第三轮

中序 : 11 [15 13 14 12]
后序 : [10 15 14 13 12 ] 11

此时划分 :

[] 11 [ 15 13 14 12]
[15 14 13 12 ] 11

此时结构为 :

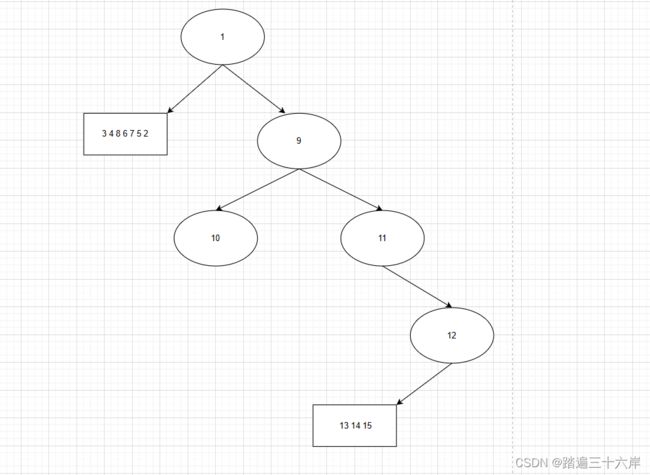
• 第三轮

中序 : [ 15 13 14 12]
后序 : [15 14 13 12 ]

此时划分 :

[15 13 14 ] 12 []
[15 14 13 ] 12 

此时结构 :

• 第四轮

中序 : [ 15 13 14]
后序 : [15 14 13 ]

此时划分 :

[15] 13 [14]
[15 14] 13

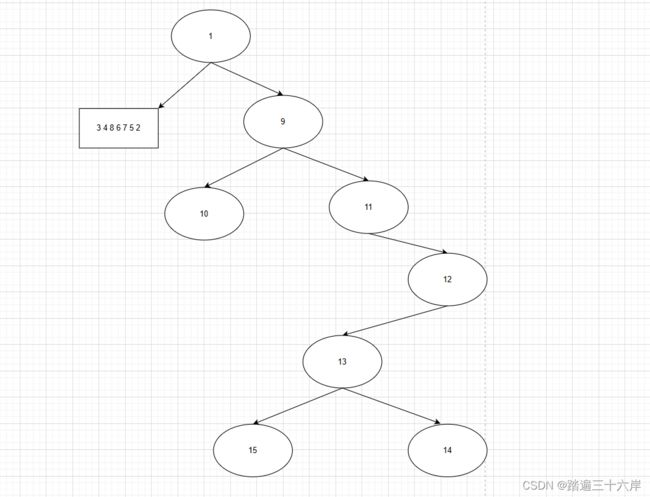
左边也是一样的 , 这里就不展示了 , 大家自己动手试试 …
直接展示完整版 :

这期就到这里 , 下期再见!