【3】强化学习之动态规划（策略迭代和价值迭代）

给定一个马尔科夫决策过程（MDP）$<\mathcal{S},\mathcal{A},\mathcal{P},\mathcal{R},\gamma >$，根据状态转移概率$\mathcal{P}$是否已知，强化学习可分为基于模型（Model-based）和无模型（Model-free）的两种学习方法。而动态规划是基于模型的强化学习方法，分为策略迭代（policy iteration）和价值迭代（value iteration）两种。

1. 策略迭代

策略迭代包括策略评估和策略改进。

1) 策略评估

策略评估的目的是给定一个策略$\pi$，计算出每个状态在该策略下的价值函数，即评估每个状态的好坏。
我们首先给出当前状态$s\in \mathcal{S}$的价值函数与后继状态$s^{\prime }$的价值函数之间的关系：
$$v_{\pi }(s)=\sum _a\pi (a|s)\left(\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\pi }(s^{\prime })]\right)\text{\hspace{1em}(1)}$$
其中，$\pi (a|s)$为待评估的策略，是已知的。奖励$r\in \mathcal{R}$，折扣因子$\gamma$，转移概率$p(s^{\prime },r|s,a)$也是已知的。因此方程(1)中唯一的未知数是状态价值函数$v_{\pi }(s^{\prime })$，且有$|\mathcal{S}|$个未知数和$|\mathcal{S}|$个等式的线性方程组。理论上，该方程可以被直接解出来，但计算过程较复杂，因此我们采用迭代的方式来解决此问题，这里选择高斯-赛德尔迭代法：

$$v_{k+1}(s)=\sum _{a\in \mathcal{A}}\pi (a|s)\left(\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_k(s^{\prime })]\right)\text{\hspace{1em}(2)}$$
其中下标$k$为迭代次数，给定方程一个初始解，例如$(0,0,...,0)$，通过迭代直到收敛到一个最优解。
以下为策略评估的伪代码：
\rule[0pt]{17.8cm}{0.2em} 输入待评估的策略$\pi$，设置一个决定评估精度的$\theta >0$，初始化非终止状态$s\in {\mathcal{S}}^{+}$的价值$V(s)$，而终止状态的价值$V(terminal)=0$

$\text{Loop:}$
  $\Delta \leftarrow 0$
  $\text{Loop for each }s\in S:$
    $v\leftarrow V(s)$
    $V(s)\leftarrow {\sum }_a\pi (a|s)\left({\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma V(s^{\prime })]\right)$
    $\Delta \leftarrow \max (\Delta ,|v-V(s)|)$
$\text{Until}\Delta <\theta$

\rule[0pt]{17.8cm}{0.2em}

\\[30pt]

• 例1 ：考虑下面4×4的网格图
  
  该MDP描述为：
  • $\mathcal{S}$：非终止状态集$\mathcal{S}=\{1,2,...,14\}$
  • $\mathcal{A}$：对于$\mathcal{S}$中的每个状态有4种可能的动作$\mathcal{A}=\{\text{up,down,left,right}\}$
  • $\mathcal{P}$：当前状态$s$选择任一动作$a$后只有一个确定的下一个状态和收益，即$s^{\prime }和r$唯一。因此我们有$p(s^{\prime },r|s,a)=1$
  • $\mathcal{R}$：到达终止状态之前，所有的动作收益$R=-1$
  • $\gamma$：$\gamma =1$，即无折扣

注意，每个动作会导致状态转移，但当动作会导致智能体移出网格时，状态保持不变。假定我们需要评估的策略为均等的随机策略，即：
$$\pi (\text{up}|s)=\pi (\text{down}|s)=\pi (\text{left}|s)=\pi (\text{right}|s)=0.25,\forall s\in \mathcal{S}$$
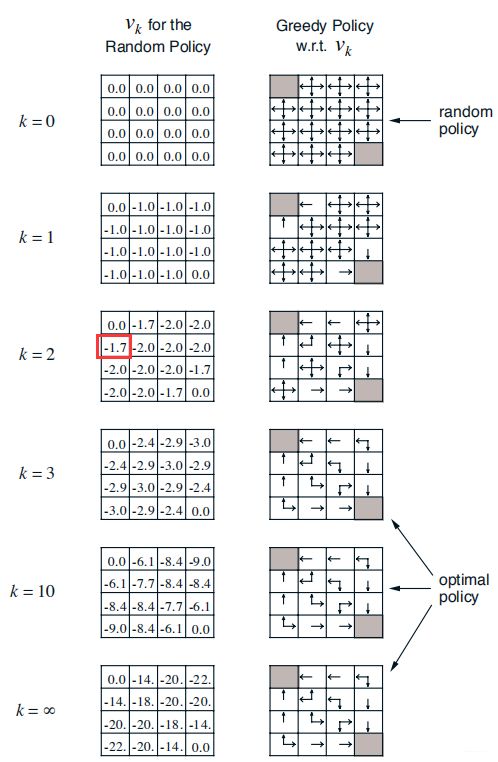
下图为迭代过程中14个状态的价值函数变化过程，我们可以看出当k=3时，已经达到了optimal policy。

根据公式(2)，我们计算k=2时，状态4的价值函数：
$$v_2(4)=0.25\times (-1+0)+0.25\times (-1-1)+0.25\times (-1-1)+0.25\times (-1-1)=-1.75$$
保留两位有效数字便是-1.7。

2) 策略改进

计算一个给定策略下的价值函数的目的是为了找出更好的策略。假定对于给定的一个策略，我们已经计算出在该策略下所有状态的价值函数$v_{\pi }(s),s\in S$。对于某个状态$s$，我们想知道是否应该选择一个不同于给定的策略的动作$a\ne \pi (s)$。一个很自然的方法是当已知当前策略下的价值函数时，在每个状态处采用贪婪策略对当前策略进行改进，即
$${\pi }_{l+1}(s)=\underset{a}{\mathrm{argmax}}{q}_{{\pi }_l}(s,a)=\underset{a}{\mathrm{argmax}}\left(\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\pi }(s^{\prime })]\right)\text{\hspace{1em}(3)}$$
假定在策略评估阶段我们迭代10次（k=10）来计算策略${\pi }_0$下所有状态的价值函数，随后进行策略改进。下图为k=10时的价值函数以及对应的贪婪策略，我们以状态4和5为例来说明怎样做策略改进：

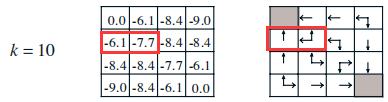
• 状态4：
  $$\begin{array}{rl}{\pi }_1(4)& =\underset{a}{\mathrm{argmax}}\{q_{{\pi }_0}(4,\text{up}),q_{{\pi }_0}(4,\text{down}),q_{{\pi }_0}(4,\text{left}),q_{{\pi }_0}(4,\text{right})\}\\ & =\underset{a}{\mathrm{argmax}}\{-1+0,-1-8.4,-1-6.1,-1-7.7\}\\ & =\{\text{up}\}\end{array}$$
  根据以上的计算可知在状态4的改进策略为：
  $$\pi (\text{up}|4)=1，\pi (\text{down}|4)=\pi (\text{left}|4)=\pi (\text{right}|4)=0$$
• 状态5：
  $$\begin{array}{rl}{\pi }_1(5)& =\underset{a}{\mathrm{argmax}}\{q_{{\pi }_0}(5,\text{up}),q_{{\pi }_0}(5,\text{down}),q_{{\pi }_0}(5,\text{left}),q_{{\pi }_0}(5,\text{right})\}\\ & =\underset{a}{\mathrm{argmax}}\{-1-6.1,-1-8.4,-1-6.1,-1-8.4\}\\ & =\{\text{up,left}\}\end{array}$$
  根据以上的计算可知在状态5的改进策略为：
  $$\pi (\text{up}|5)=\pi (\text{left}|5)=0.5，\pi (\text{down}|4)=\pi (\text{right}|4)=0$$

3) 策略迭代过程

策略迭代包括策略评估和策略改进两个步骤。在策略评估中，对于给定的一个策略，通过迭代法计算得到该策略下所有状态的价值函数；然后在策略改进中利用该价值函数和贪婪策略得到新的策略。如此循环下去，最终得到最优策略。下面为策略迭代的流程。

\rule[0pt]{17.8cm}{0.2em}

1. 初始化
   对$s\in S$，任意设定$V(s)\in \mathbb{R}$以及策略${\pi }_0$，一个决定评估精度的$\theta >0$
2. 策略评估
   $\text{Loop:}$
     $\Delta \leftarrow 0$
     $\text{Loop for each }s\in S:$
       $v\leftarrow V(s)$
       $V(s)={\sum }_{s^{\prime },r}p(s^{\prime },r|s,\pi (s))[r+\gamma V(s^{\prime })]$
       $\Delta =\max (\Delta ,|v-V(s)|)$
   $\text{Until}\Delta <\theta$
3. 策略改进
   $policy\text{-}stable=true$
   $\text{For each}s\in S:$
     $old\text{-}action=\pi (s)$
     $\pi (s)=\underset{a}{\mathrm{argmax}}\left({\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)+[r+\gamma v(s^{\prime })\right)$
     如果$old\text{-}action\ne \pi (s)$，那么 $policy\text{-}stable=false$
   如果 $policy\text{-}stable$为$true$，那么停止并$v\approx v^{\ast }$，以及$\pi \approx {\pi }^{\ast }$；否则跳转到步骤2

\rule[0pt]{17.8cm}{0.2em}

\\[30pt]

2. 价值迭代

从策略迭代的流程来看，进行策略改进之前要得到价值函数的收敛，而价值函数的收敛需要迭代多次，那么问题来了，在进行策略改进之前我们是否需要等到价值函数的收敛呢？回答是肯定的。如果我们在评估一次策略之后就进行策略改进，这种方法称为价值迭代（value iteration）。
\rule[0pt]{17.8cm}{0.2em} 初始化
  对$s\in S$，任意设定$V(s)\in \mathbb{R}$，一个决定估计精度的$\theta >0$
$\text{Loop}:$
  $\Delta \leftarrow 0$
  $\text{Loop for each}s\in S:$
    $v\leftarrow V(s)$
    $V(s)\leftarrow \underset{a}{\max }\left({\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma V(s^{\prime })]\right)$
    $\Delta =\max (\Delta ,|v-V(s)|)$
$\text{Until}\Delta \leftarrow \theta$
输出$\pi (s)=\underset{a}{\mathrm{argmax}}\left({\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma V(s^{\prime })]\right)$

\rule[0pt]{17.8cm}{0.2em}

\\[30pt]

3. 寻宝问题

下面的代码是解决以下寻宝问题，其中红色圆圈为智能体，黑色方框为陷阱，箱子为宝藏。
策略迭代和价值迭代的python代码

参考资料：
（1）Richard S. Sutton and Andrew G. Barto著, 俞凯译《强化学习》第二版
（2）张斯俊. 欢迎大家入坑Reinforcment Learning【知乎】
（3）郭宪, 方勇纯. 《深入浅出强化学习：原理入门》