强化学习实战之策略迭代
Policy Iteration
在动态规划那一章我们知道在给定完备的环境模型的情况下可以用策略迭代的方式来求解最优策略,这次我们主要用gym中的FrozenLake-v0环境来试验策略迭代。
from gym import envs
import gym
import numpy as np
import time
from IPython.display import clear_output
我们首先导入必要的包然后熟悉一下gym
# show all environments
total_env = envs.registry.all()
env_ids = [i.id for i in total_env]
print(len(env_ids))
[out]:
859
可以看到gym中总共有859个环境,我们选择FrozenLake-v0环境,并将它渲染出来。
#show the FrozenLake-v0 environment
try:
env = gym.make('FrozenLake-v0')
except:
print("unable to load env!")
env.render()
env.close()
[out]:
SFFF
FHFH
FFFH
HFFG
其中S表示Start,是Agent开始运动的地方;G是Goal,是Agent的目标,到达G之后一幕结束;F是Frozen代表冰面,是Agent可以行走的地方;H代表Hole,一旦Agent掉进去这一幕就结束了。整个游戏过程中只有走到G才会获得一个reward,在其他地方行走包括遇到H都不会获得reward,另外有一点必须要注意:在该环境中,设计者考虑到了冰面很滑,所以Agent采取某个动作后并不一定会到达预期的位置!
# several key points of the environment
action_space = env.action_space
observation_space = env.observation_space
print(action_space, type(action_space))
print(observation_space, type(observation_space))
print(action_space.sample()) # randomly sample from 0,1,2,3
print(observation_space.contains(14)) # judge wheather the state is in the state set
print(action_space.n) # number of actions
print(env.nA, env.nS) # number of actions in this env, number of states in this env.1
[out]:
Discrete(4)
Discrete(16)
0
True
4
4 16
可以看到动作和状态都是离散的值,该环境总共共有16个状态,4个动作。状态从左往右,从上往下为 [ 0 , … , 15 ] [0, \dots , 15] [0,…,15] ,动作为 [ 0 , 1 , 2 , 3 ] [0,1,2,3] [0,1,2,3] ,分别代表左、下、右、上。
'''
check the 14th state's dynamic
each state has four actions: 0=>up; 1=>down; 2=>left; 3=>right
Notice that dynamic is different from policy.
Policy determins the probability of choosing a action at a specific state.
Dynamic relates to the environment, for example, imagine there's a boat driving on
the lake, at a specific state it turned left, however, the place it finally reached
is determined by the whole environment such as wind, stream, etc.
When arrived at state[15], get 1 reward, then the episode is finished.
When agent stuck into a "Hole" the episode finishs without any reward!
'''
print("state 14")
for key, value in env.P[14].items():
print(key,':', value)
print('\n'*2)
print('state 4')
for key, value in env.P[4].items():
print(key, ':', value)
print("state 5")
for key, value in env.P[5].items():
print(key, ':', value)
[out]:
state 14
0 : [(0.3333333333333333, 10, 0.0, False), (0.3333333333333333, 13, 0.0, False), (0.3333333333333333, 14, 0.0, False)]
1 : [(0.3333333333333333, 13, 0.0, False), (0.3333333333333333, 14, 0.0, False), (0.3333333333333333, 15, 1.0, True)]
2 : [(0.3333333333333333, 14, 0.0, False), (0.3333333333333333, 15, 1.0, True), (0.3333333333333333, 10, 0.0, False)]
3 : [(0.3333333333333333, 15, 1.0, True), (0.3333333333333333, 10, 0.0, False), (0.3333333333333333, 13, 0.0, False)]
[out]:
state 4
0 : [(0.3333333333333333, 0, 0.0, False), (0.3333333333333333, 4, 0.0, False), (0.3333333333333333, 8, 0.0, False)]
1 : [(0.3333333333333333, 4, 0.0, False), (0.3333333333333333, 8, 0.0, False), (0.3333333333333333, 5, 0.0, True)]
2 : [(0.3333333333333333, 8, 0.0, False), (0.3333333333333333, 5, 0.0, True), (0.3333333333333333, 0, 0.0, False)]
3 : [(0.3333333333333333, 5, 0.0, True), (0.3333333333333333, 0, 0.0, False), (0.3333333333333333, 4, 0.0, False)]
[out]:
stat 5
0: [(1.0, 5, 0, True)]
1: [(1.0, 5, 0, True)]
2: [(1.0, 5, 0, True)]
3: [(1.0, 5, 0, True)]
可以看到在不同的”状态—动作“二元组有其对应的动态特性,在每一块冰面上每个动作都对应3个动态特性,分别以元组的形式给出,代表了 transition_probability,next_state,reward,done。注意,只有当Agent掉入Hole或者达到Goal时done才为True。在Hole状态无论采取什么动作都无济于事,状态不会改变,收益为0,并且游戏结束。
熟悉完了环境我们就正式开始写policy iteration!
我们首先来写一个在一幕中执行策略的函数,该函数返回这一幕的总步数和回报。
# define policy execute one episode similar to MC
def execute_policy(env, policy, render=False):
total_steps,total_reward, steps = 0, 0, 0
observation = env.reset()
while True:
if render:
env.render()
clear_output(wait=True)
time.sleep(0.3)
action = np.random.choice(action_space.n, p=policy[observation])
observation, reward, done, _ = env.step(action)
steps += 1
total_steps += 1
total_reward += reward
if done:
if render:
print('total steps: %d' % steps)
print("return of this episode: ", total_reward)
time.sleep(3)
clear_output()
break
return total_steps, total_reward
在策略迭代中第一步是策略评估。
def evaluate_policy(env, policy, gamma=1.0, threshold=1e-10):
value_table = np.zeros(env.nS)
while True:
delta = 0.0
# for each state
for state in range(env.nS):
Q = []
for action in range(env.nA): # full backup
# the dynamic of each (state, action) tuple
q = sum([trans_prob*(reward + gamma*value_table[next_state]*(1.0 - done)) \
for trans_prob, next_state, reward, done in env.P[state][action]])
Q.append(q)
vs = sum(policy[state] * Q)
delta = max(delta, abs(vs-value_table[state]))
value_table[state] = vs
if delta < threshold:
break
return value_table
对应着书中的算法和公式一起看:

v k + 1 ( s ) ≐ E π [ R t + 1 + γ v k ( S t + 1 ) ∣ S t = s ] = ∑ a π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v k ( s ′ ) ] (1) \begin{aligned}v_{k+1}(s) & \doteq \mathbb{E}_{\pi}\left[R_{t+1}+\gamma v_{k}\left(S_{t+1}\right) | S_{t}=s\right] \\&=\sum_{a} \pi(a | s) \sum_{s^{\prime}, r} p\left(s^{\prime}, r | s, a\right)\left[r+\gamma v_{k}\left(s^{\prime}\right)\right]\end{aligned}\tag{1} vk+1(s)≐Eπ[Rt+1+γvk(St+1)∣St=s]=a∑π(a∣s)s′,r∑p(s′,r∣s,a)[r+γvk(s′)](1)
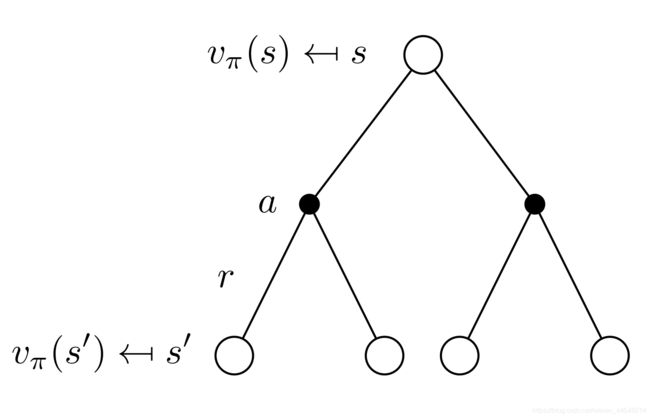
v π ( s ) = ∑ a ∈ A π ( a ∣ s ) ⋅ q π ( s , a ) (2) \begin{aligned}v_{\pi}(s)=\sum_{a \in \mathcal{A}} \pi(a | s) \cdot q_{\pi}(s, a)\end{aligned}\tag{2} vπ(s)=a∈A∑π(a∣s)⋅qπ(s,a)(2)
q π ( s , a ) = r ( s , a ) + γ ∑ s ′ ∈ S p ( s ′ ∣ s , a ) ⋅ v π ( s ′ ) (3) \begin{aligned}q_{\pi}(s, a)&=r(s,a)+\gamma \sum_{s^{\prime} \in \mathcal{S}} p\left(s^{\prime} | s, a\right)\cdot v_{\pi}\left(s^{\prime}\right)\\\end{aligned}\tag{3} qπ(s,a)=r(s,a)+γs′∈S∑p(s′∣s,a)⋅vπ(s′)(3)
我们首先初始化value_table,将每个状态价值都设为0。”Loop“即代码中的 whiel True:我们反复循环也就是不停地利用 v k , v k + 1 v_{k},v_{k+1} vk,vk+1 迭代,直到满足threshold的限定条件。还记得DP的特点是期望更新,每一次更新状态价值都用到了所有单步后继状态,因此要对每个状态的每个动作运算!
需要注意 sum()是对列表中的所有元素求和,所以在计算q时sum内部用了一个比较的列表解析;在计算vs时,Q和policy[state]是相同维度的,其中Q是list,policy[state]是ndarray,这两者相乘是对应位置相乘,得到的结果仍然是ndarray,每个元素分别是 π ( a ∣ s ) ⋅ q π ( s , a ) \pi(a | s) \cdot q_{\pi}(s, a) π(a∣s)⋅qπ(s,a) ,再来一个 sum就得到了vs
==注意:==当采取某个确定策略 π ( s ) = a τ \pi(s)=a_{\tau} π(s)=aτ 时,即 π ( a = a τ ∣ s ) = 1 \pi(a=a_{\tau}|s)=1 π(a=aτ∣s)=1 ,此时 v π ( s ) = q π ( s , a ) v_{\pi}(s)=q_{\pi}(s,a) vπ(s)=qπ(s,a) !在DP中策略是确定的,所以有些代码中q和v的计算公式相同。
while True:
delta = 0
# For each state, perform a "full backup"
for s in range(env.nS):
v = 0
# Look at the possible next actions
for a, action_prob in enumerate(policy[s]):
# For each action, look at the possible next states...
for prob, next_state, reward, done in env.P[s][a]:
# Calculate the expected value. Ref: Sutton book eq. 4.6.
v += action_prob * prob * (reward + discount_factor * V[next_state])
# How much our value function changed (across any states)
delta = max(delta, np.abs(v - V[s]))
V[s] = v
# Stop evaluating once our value function change is below a threshold
if delta < theta:
break
策略评估的主循环也可以这么来写,用了enumerate来获取动作和其对应的概率。
接下来是策略改进部分。
# policy improvement
def improve_policy(env, value_table, policy, gamma=1.0):
optimal = True
execute_policy(env, policy, render=True)
# calculate q
for state in range(observation_space.n):
Q_table = np.zeros(env.nA)
for action in range(action_space.n):
Q_table[action] = sum([trans_prob*(reward + gamma*value_table[next_state]*(1.0-done)) \
for trans_prob, next_state, reward, done in env.P[state][action]])
a = np.argmax(Q_table)
if policy[state][a] != 1.:
optimal = False
policy[state] = 0.
policy[state][a] = 1.
return optimal
对每个位置的每个动作计算q,并选择最大的那一个获取它的动作然后把对应的概率设置成1,不断循环直到每个位置都选出了最优动作,做出了策略改进为止。
最后综合这两个过程就是策略迭代了。
# policy iteration
def iterate_policy(env, gamma=1.0, threshold=1e-10):
policy = np.ones((env.nS, env.nA)) / env.nA
for i in range(1000):
print('{:=^80}'.format('iteration %i'%(i+1)))
time.sleep(3)
value_table = evaluate_policy(env, policy, gamma, threshold)
if improve_policy(env, value_table, policy, gamma):
print("iterated %d times" %(i+1))
break
return policy, value_table
从上面的代码不难看出策略改进要等到策略评估完全进行完了以后才能开始,这也是策略迭代比较耗时的地方,之后的价值迭代将会在此处有一个改进。
得到了所谓的最优策略之后不妨测试一下它的表现,运行一定次数看看有多少次是能够成功走到G,平均每一次要走多少步。
# check the so called optimal policy's performance
def check_policy(policy, episodes=100):
successed_nums = 0
total_steps = 0
for i in range(episodes):
one_episode_steps, one_episode_return = execute_policy(env, policy)
total_steps += one_episode_steps
if one_episode_return == 1.0:
successed_nums += 1
return total_steps / episodes, successed_nums / episodes
运行策略迭代,获得最优策略和相应的价值函数
optimal_policy, optimal_value_tabel = iterate_policy(env)
print("policy: ", optimal_policy, sep='\n')
print("value_tabel: ", optimal_value_tabel, sep='\n')
[out]:
iterated 3 times
policy:
[[1. 0. 0. 0.]
[0. 0. 0. 1.]
[0. 0. 0. 1.]
[0. 0. 0. 1.]
[1. 0. 0. 0.]
[1. 0. 0. 0.]
[1. 0. 0. 0.]
[1. 0. 0. 0.]
[0. 0. 0. 1.]
[0. 1. 0. 0.]
[1. 0. 0. 0.]
[1. 0. 0. 0.]
[1. 0. 0. 0.]
[0. 0. 1. 0.]
[0. 1. 0. 0.]
[1. 0. 0. 0.]]
value_tabel:
[0.82352941 0.82352941 0.82352941 0.82352941 0.82352941 0.
0.52941176 0. 0.82352941 0.82352941 0.76470588 0.
0. 0.88235294 0.94117647 0. ]
测试表现,平均步数和准确率如下,可以看出来还有很多改进的空间。
ave_steps, acc = check_policy(optimal_policy, episodes=5000)
print("ave_steps: ", ave_steps)
print("acc: ", acc)
[out]:
ave_steps: 44.3846
acc: 0.7452
代码地址
policy iteration.py
policy iteration.ipynb
参考资料
《强化学习原理与Python实现》肖智清