初见安~好久好久没写博客了……感觉还是有必要写的。
拿去年济南的题目训练了一下，状态还不错，写一下自己写过了的题目的题解。
M Best Carry Player
题意：给你n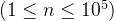
个数，交换他们的顺序使依次相加后总的进位次数最少（十进制），并输出进位次数。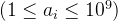
很显然，加法中两数相加最多进位进1；单看每一位就能发现，其实进位次数跟顺序压根没关系。
所以写一个高精加法模拟加法过程算进位次数就完了。
注意数据范围，最多可以达到14位数。
#include
#include
#include
#include
#include
#include
#include
#include
#include
E Identical Parity
题意：T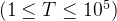
组数据，每次给定一个n和k
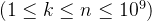，问是否存在一个n的排列，满足所有长度为k的子区间内的数的和的奇偶性相同。
显然我们只需要考虑这长度为n的排列中每个数的奇偶个数能否满足。
有一些特殊情况容易想到：
- k=1时，除非n=1，否则都无法满足题意；
- k为偶数时，一定可以满足题意（奇偶交错的排列均可）；
- k为奇数(k != 1)时，我们需要额外进行讨论了。
因为若长度为n的排列是满足奇偶性的条件，那么任意长度为l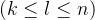
的区间都满足区间奇偶性的条件。（不一定满足为一个合法排列，即奇数个数=偶数个数（+1）的条件）所以我们首要考虑奇偶性的条件如何满足。
首先考虑第一个长度为k的区间，k是奇数，故一定是奇数个数大于偶数个数（否则凑不了多少长度），不妨令x+1为奇数个数，则x为偶数个数。（2x+1=k）
令此时的构造排列为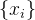
，其中xi为0或者1表示为偶数or奇数。
假设我们已经构造好了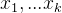
，对于下一个区间
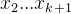，相当于在前一个区间的基础上减去x1加上x_{k+1}，且sum的奇偶性不变。换言之，
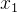与
奇偶性相同。也就是说：对于任意长度的排列，我们构造好了前k个的奇偶性后，之后每一位的奇偶性都是确定的。也可以说：每个区间内奇数和偶数个数都是一样的。
所以我们只需要考虑如何对这x+1个奇数和x个偶数如何进行排序。
易知n=2k时，即奇数比偶数多两个，一定无法构造出来；推出n=tk时，奇数会比偶数多t个。所以要满足题意，我们需要在后面补至少t-1个偶数。也就是说此时构造的x序列，至少前t-1个可以是偶数。即：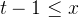
。
同理，假如我们补完所有0后继续往后面补1，至多可以补多少个1呢？那就是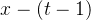
个，也就是多了多少个0就可以补多少个1。
所以我们可以得出当![n \in[tk, (t+1)k]](http://img.e-com-net.com/image/info8/98ac692ab36546ba9470bf8728a175f3.png)
时，只有![n \in [tk+t-1,tk+x+x-(t-1)]](http://img.e-com-net.com/image/info8/2045b9d3d1204f3cb6ec0c3675de1b7e.png)
时构造有解。
举个例子：k=3时，我们容易想到n=3,4,5都构造有解。而n=7就是最大的一个满足情况的n。
我们只能构造奇偶序列如：011 011 0，把0放在最前面，这样会优先把0复制在最后。
再比如k=5时，我们可以构造前5个为00111，这样可以满足n=11~13，17的情况。
代码就是公式抄一遍。
#include
#include
#include
#include
#include
#include
#include
#include
#include
D Frozen Scoreboard
题意：
（bushi）
n个题目m个队伍，你有一个封榜前的榜单，已知每个队伍（相互独立）每个题目的状态和最终通过提数和罚时，问你是否存在一个终榜满足这些条件并构造出来。（具体的看原题目吧）
说白了就是模拟……没通过和没提交的题目没有任何作用，原样输出就好；+的题目要记得加上wa的罚时，剩下的就是？的题目看要选哪些通过。
n很小啊只有13，那就最多13个？。我们把？全取出来，需要通过的题目数是已知的，最坏情况是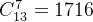
，m又只有1e3，所以暴力枚举。枚举完了过后考虑如何分配剩余的罚时。
首先每个题目240罚时起步；其次20，20地尽量把赛后的未通过提交的罚时用完，最后再用每个题剩的59min去凑零碎的剩余罚时。
思路很简单但是实现起来挺恶心的……要存的东西很多。
以及对于No的判定，要提前把 ？不够多；罚时不够减；罚时凑不上等一看就凑不出来的情况判掉。
上代码了
#include
#include
#include
#include
#include
#include
#include
#include
#include
