最后我们来探究红黑树的删除算法,相比插入操作,它的情况更复杂一些。因此直接考虑很容易撞到南墙,我们更需要利用转化与化归的思想(还记得高中数学四大思想方法吧,这里一样适用),通过提升变化,把红黑树映射成一颗B-树,并站在后者的角度,反过来理解前者的原理。但我们更需要关心重构操作,也就是一系列的旋转和修复过程,并在此过程中留意他的重构次数都是$O\left( 1 \right)$级别的。
这个删除操作还挺复杂的。。。可以说繁琐到了让人恶心的地步,各位做好心理准备。可以在旁边准备个塑料袋或者盆什么的,省的没地方。。。
先给出一些辅助函数,方便后续使用
Position p=NULL; //用于存储父节点的地址 Position SearchIn(Position v,int e,Position& parent){//返回指向父节点指针的引用,因为后续要做左值 if (!v || (e == v->value)) return v; //递归基,如果直接命中或不存在则返回 parent=v; //一般情况则是先记下当前节点,然后深入一层。 return SearchIn((e < v->value ? v->left : v->right), e, parent); }//返回值指向命中节点,parent为其父。 Position Search(int target,RedBlackTree T){ return SearchIn(T, target, p); } Position GetParentOf(int e){ Search(e, fir); return p; } //由于我写的结构体里没有parent指针,所以通过这个函数等效获取。 Position GetParentOf(Position T){ //得到T的父节点 Search(T->value, fir); return p; } int IsLChild(Position p){ //判断p点是否为某个节点的左孩子 if (GetParentOf(p) != fir && GetParentOf(p)->left == p) return 1; else return 0; } Position& FromParentTo(Position p){ //返回某个节点来自父亲的指针 if(GetParentOf(p) == fir) return p; //处理P是根的情况 if (GetParentOf(p) ->left ==p) // p is leftChild return GetParentOf(p)->left; else return GetParentOf(p)->right; }
红黑树的删除也类似BST删除,自顶向下(参看前面二叉树实现一文),如果被删除节点X并非叶子,我们会考虑用它的直接后继(右子树上的最小元素)代替,这样X顶多有一个右孩子,或者X被转移到叶子的位置,直接删除即可。但有一些情况需要仔细分析,因为红黑树规则有其他的限制。
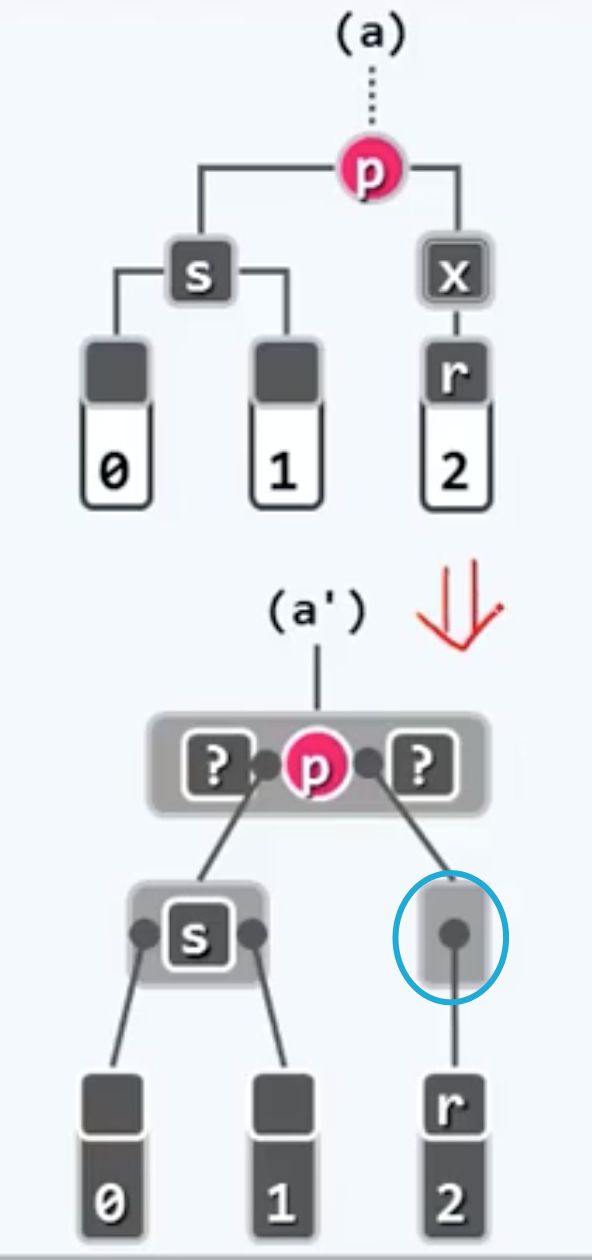
比如在这副图中节点x在被删除之后,将由它的某一个后代r来替代,这样一来红黑树的性质就未必都能继续满足了,验证一下:首先红黑树的根、外部节点没有受影响,但在此局部有可能会出现两个连续的红色节点,而更重要的是在被删除节点所在的路径上,黑节点的数目 可能变化,第四条规则不一定能满足了。另外有一大类的情况,还是非常容易处理的。就是被删除节点x 与它的替代者r之间有一个是红的(当然不可能全红),如上下这两张图的情况。
这种情况只要把替代者r染为黑色即可,就保证第4条规则不受影响了。原因在于,从删除操作之前的树结构可见,在此局部都包含一条指向红节点的虚边,上篇说过这类虚边对于黑高度是没有影响的,因此在把r染黑之后,都相当于删除了一条虚边,因此所有外部节点的黑深度不受影响。红色叶子的删除还好说,问题就在于如果这叶子是黑色的,删除之后规则4就被破坏了。解决思路就是:保证从上到下删除期间树叶始终是红色的。下面详细分析一下这一类情况。
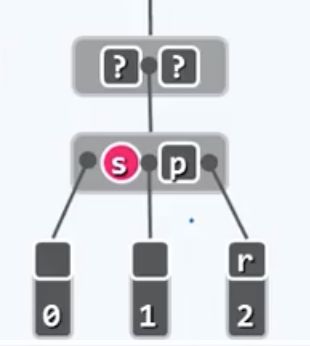
有可能被删除节点和替代者都是黑色的,
这种情况我们也称之为双黑,此时这两个节点所属的那条路径而言黑长度必然会减少一个单位,从而必然违背红黑树的第四条规则。而且不幸的是,前面简明的方法,也不再有效。在给出新的方法之前,我们或需要从另一个角度来体会,问题究竟出在哪。什么角度呢 ?当然啦,就是B树。如果x和r都是黑色的,那么在对应的4阶B树中,x将独自成为一个内部节点
于是在唯一的这个关键码被删除之后,这个节点也就发生下溢。因此我们的调整算法与其说是在红黑树中修复双黑缺陷,不如说是在B树中修复下溢缺陷。为此我们需要考察两个节点:首先是删除之后,节点r的父亲p;此外我们还需要在原树中考察节点r的兄弟S。
先给出在某处删除节点的办法,和BST很像
Position removeAt(Position x){ Position temp; if (x->left && x->right) { temp=FindMin(x->right); x->value=temp->value; x->right=removeAt(x->right); } else{ temp=x; if(!x->left) x=x->right; else if (!x->right) x=x->left; free(temp); } return x; }//返回被删除节点的位置
以下我们就分4种情况分别处置
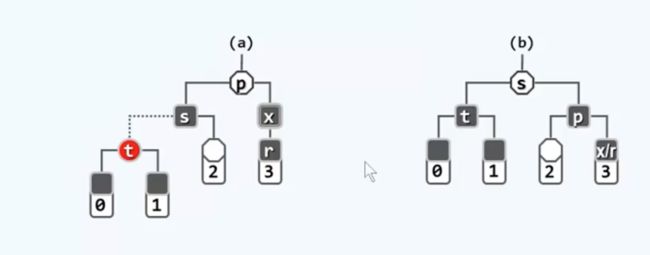
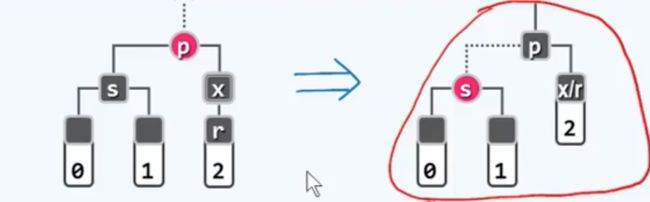
第一种情况:S为黑,且至少有一个红色孩子
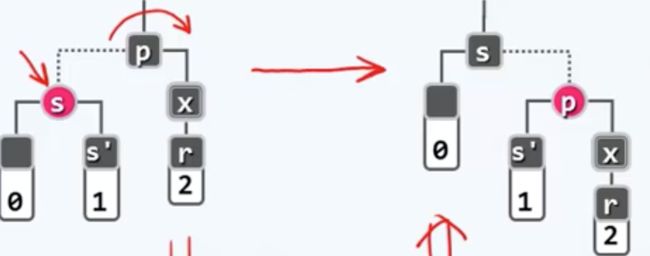
以一字型为例(左),其余的情况都与之对称或相似。调整办法就是做相应旋转和重新染色(右)。染色规则是:r继续保持黑色,而t和p都染黑,而s将继承此前根节点p的颜色。
这里的4棵子树其黑高度都是一样的,因此调整之后红黑树的所有性质都恢复了。这一转换方法并非偶然,而是有着深刻的原理,就是B树。接下来就让我们转到B树的角度,来反观这种变换的效果。
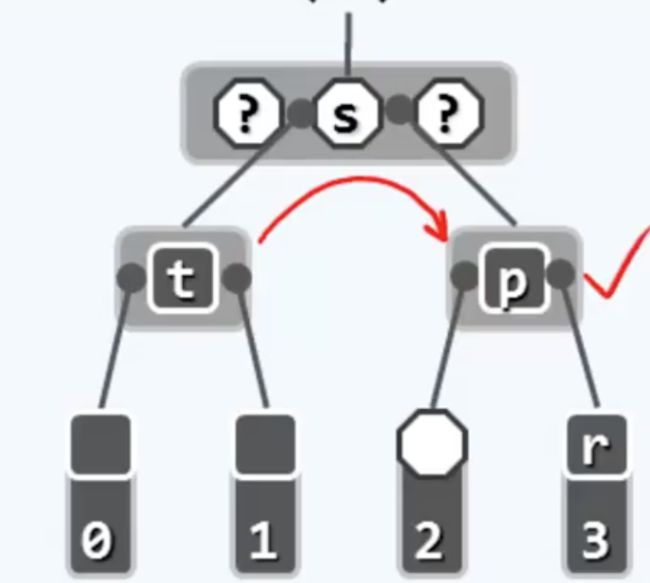
可以看到,双黑缺陷对应于一次下溢,所幸的是,发生下溢的这个节点拥有一个足够富有的兄弟,可以通过旋转消除下溢。具体来说下溢节点将从父亲那借得一个关键码,而父亲再向那个兄弟借入一个关键码以填补空缺。
经过这样的旋转,可以看到下溢节点得到了修复。
接下来把修复之后的B树,还原为对应的那棵红黑树即可,与直接在红黑树上所做的变换是完全一致的。
新的这个关键码 会依然继承它前任的颜色,所以绝对不会在其他位置再次造成双黑。从这个意义上讲,这种情况是相对简单的,体现在可以仅通过一次旋转完成。换句话说至少有一个红色孩子。那这种情况既然是简单的,我们也很容易得知:更难的情况是没有一个孩子为红。那又该如何应对呢?
第二种情况:S为黑,两个孩子都为黑。但是P是红色。
这种情况又进而分为两种子情况,它们的区别就在于:此时的父节点P究竟是红还是黑,我们先讨论红色的情况。
首先将此前的红黑树 转换为对应的B树,依然在这个位置上发生了一次下溢。此时我们并不能实施旋转调整,原因是此时的兄弟节点s已经没有余粮了,自己已经处于下溢的边缘试探了,并不足以借出任何的关键码。还记得之前怎么处理的吧,合并。从父节点中取出一个元素,并且以它作为粘合剂,将左和右两个节点合二为一。修复的结果如下:
然后变换回对应的红黑树,就可以得到在红黑树中的一种可行调整方案:
现在站在红黑树的角度来观察这个过程,结果相当于r保持此前的黑色,而s由黑转红,同时p由红转黑。所以在红黑树中的上述调整过程,完全等效于在B树中某个节点通过与它的兄弟合并来消除下溢。而且这一个局部双黑缺陷的修复,也意味着红黑树的性质能够得以在全局得到恢复,一次修复,彻底修复。
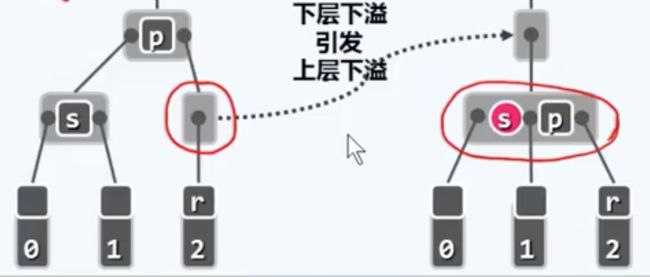
第三种情况:S为黑,两个孩子都为黑。而且P是黑色。
同样的站在B树的角度来看,此时依然会发生一次下溢,而且同样只能通过兄弟节点的合并来加以消除。
与第二种情况的不同之处在于,此时的元素p是独自成为一个内部节点,因此当这个唯一的元素p被借出之后,此前的父节点将注定发生下溢。也就是说,在这种情况下双黑缺陷有可能会向上传播一层,甚至继续上传,直到最后的树根。如果还采用老办法修复,至多也就发生logn次,那问题来了,拓扑结构也会随之变化logn次?这可不是个好消息。
其实只要回到红黑树,就可以形象地理解这个复杂的调整
需要再次强调的是:经过这样的调整,红黑树的拓扑结构没有实质变化。也就是说 整个调整过程所执行的重构操作,不超过O(1)依然有可能落实。以下 我们只剩下最后一种情况。也就是兄弟节点s有可能不是黑色,而是红色。
第四种情况:S为红,孩子均为黑
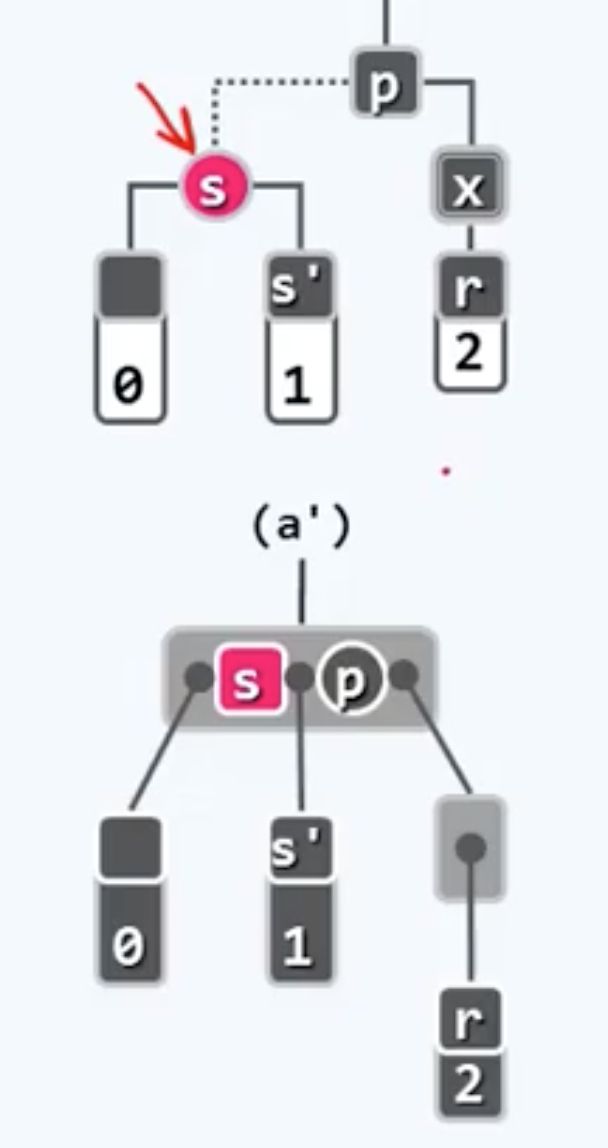
参照普通BST的删除,我们只需要转化为之前的某种情况就行了,而不用另起炉灶。为此我们需要再次站在对应B树的角度:
此时的p和s共同的结为一个3分支的内部节点,在此时的B树中,只需令s和p互换颜色,而无需做任何实质的结构调整。当然在对应的红黑树中,需要做一次结构调整。具体来说就是要围绕节点p旋转,同时翻转s和p的颜色。
到这里我们或许有些失望,因为问题并没有解决。比如原先黑高度的异常依然存在。然而实际上这步转换并非没有意义,因为此前的矛盾焦点在于节点r的兄弟s为红色,现在在无形中r已经拥有了一个黑的兄弟s',于是此后必然会跳出第四种情况,而转入此前所讨论的3种情况。而更好的消息是,下面只可能转入其中的第1或者第2种情况,而不会是第3种。因为第3种的特征是父节点p必须是黑的,经过刚才的变换,p已经悄然变成红色。而1,2的情况的计算复杂度更小,因为不会向上蔓延。所以经过如此调整之后,只需再做一轮递归,整个红黑树必然会完整修复。
那么具体的代码实现就是:
void solveDoubleBlack(Position x){ //双黑缺陷的修复 Position p=GetParentOf(x); //r的父亲 if(!p) return; Position sibling= (x==p->left)? p->right : p->left;//r的兄弟 if (sibling -> col==black){ //兄弟为黑 Position temp=NULL; if( sibling ->left && sibling->left->col==red) temp=sibling->left; else if (sibling ->right && sibling->right->col==red) temp=sibling->right; if (temp) { //情况1:黑s有红色孩子 Color oldCol=p->col;//备份原来的根p的颜色, FromParentTo(p) =Rotate(sibling->value,p);//做重平衡 Position b=FromParentTo(p); //然后把新子树的左右孩子染黑 if(b->left) b->left->col=black; if(b->right) b->right->col=black; b->col=oldCol; //新树根继承原来的颜色 } else{ //情况2、3:黑s无红色孩子 sibling->col=red; //s转红 sibling->Height--; if(p->col ==red) //情况2 p->col=black; else{ //情况3 p->Height--; //颜色保持,但是黑高度减1 solveDoubleBlack(p); }}} else{ //情况4:兄弟为红 sibling->col=black; p->col=red; //s转黑,p转红 Position t= IsLChild(sibling)?sibling->left:sibling->right; FromParentTo(p)=Rotate(sibling->value,p); } solveDoubleBlack(x); } //正式的删除过程 void Delete(int e,RedBlackTree T) { Position X = Search(e, T); //X指向被删除节点 if(!X) printf("%d not found!",e); Position r=removeAt(X); if(GetParentOf(r) ==fir)//如果是根节点,将其染黑 r->col=black; if (r->col==red) //如果r为红色,直接染黑就行 r->col=black; //以下情况:原来的x(现在的r,因为被删除了嘛,然后替换了)均为黑色 solveDoubleBlack(r); }
看起来就很。。。一言难尽。这个代码暂时还有一些小问题,但是足够帮助我们理解删除过程了,可以暂且当成伪代码。 本来想着先不放上来吧,但是光看图理解的话,似是而非,所以还是看看代码实现吧。
现在作一总结,以下是删除的情况分析:
每一次删除操作 在每一高度上至多只会花费常数时间,由此可知红黑树的删除时间复杂度不会超过$O\left( \log n \right)$。通过以上概括可以发现,红黑树的删除至多只需做$\log n$次的重染色,以及常数次的结构调整。这也是红黑树优于AVL树的一个重要方面。还记得吧,在介绍红黑树伊始就提到过,这个特性对于持久性结构的实现是至关重要的。