详解优先级队列（上）【模拟实现优先级队列】

✨hello，愿意点进来的小伙伴们，你们好呐！
✨ 系列专栏：【数据结构】
本篇内容：详解优先级队列 PriorityQueue
作者简介:一名现大二的三非编程小白

引入

在前文，我们学习到了队列这种数据结构，队列中有先进先出的特性足以解决生活中的一些问题，但是美中不足的是：操作的数据可能带有优先级，一般出队列时，可能需要优先级高的元素先出队列，比如你在玩游戏的时候，有人打电话给你，这个时候手机就要优先处理打进来的电话，这种场景下，队列显然无法处理，那么我们可以使用优先级队列来处理。
那什么是优先级队列呢？ 接下来让我来好好介绍，优先级队列的介绍会分为上篇与下篇噢！

什么是优先级队列呢

优先级队列的底层是用堆来实现的，什么是堆呢？
堆其实就是在二叉树的基础上多了一些特殊的性质：
一颗完全二叉树如果它的所有元素满足，根节点的元素大小全部大于其子节点，或者根节点的元素大小全部小于其子节点。这种特殊的完全二叉树就叫做堆。
而根节点最大的就是大根堆，根节点最小的就是小根堆。

大根堆

小根堆

接下来让我们来模拟实现一下优先级队列，首先先来模拟堆的实现。

模拟实现优先级队列

堆的存储方式

从概念上，我们可以得知堆是一个完全二叉树，因此我们可以用层序遍历的方法来较高效的存储，将元素存储到数组当中。
为什么会说完全二叉树用数组存储的话比较高效呢？让我来举个例子就懂了
完全二叉树数组存储：

非完全二叉树数组存储：

我们通过对比可以得出结论：完全二叉树存储进数组中，数组的每一个位置都会存储到元素，然而非完全二叉树存储进数组时，数组中的位置会存储进null，因此浪费了不少空间，这样的话空间利用率较低。
将元素存储到数组中，有利于我们对二叉树进行还原。

堆的创建

我们想创建模拟堆的实现应该怎么做呢？
我们想来实现大根堆。

实现堆的初步思路就是这样子，我们来优化一些细节，我们先创建一个 TestHeap 类

public class TestHeap {

    public int[] elem;
    public int usedSize;//有效的数据个数

    public static final int DEFAULT_SIZE = 10;

    public TestHeap() {
        elem = new int[DEFAULT_SIZE];
    }
}

接下来将没有通过调整的数组元素添加入elem数组

public void initElem(int[] array){
    for (int i = 0; i < array.length; i++) {
        elem[i] = array[i];
        usedSize++;
    }
}

接下来我们来看看该如何调整数组使改数组符合堆的形式。

通过该图，可以发现我们所需要调整的根节点最大值为 4 ，且递减。而 4 就是 （usedSize - 1 - 1）/ 2，所以我们可以用for循环遍历从 4 递减的元素，将它们调整。

public void creatHeap(){
    for (int parent = (usedSize - 1 - 1) / 2; parent >= 0; parent--) {
        //统一的调整方法
        shiftDown(parent,usedSize);
    }

}

然后调整的方法 shiftDown（）中 先找到根节点的孩子节点，再对该树进行调整。

public void shiftDown(int parent,int len){
    int child = 2 * parent + 1;
    while(child < len){
        //判断孩子节点谁是最大的
        if(child + 1 < len && elem[child] < elem[child + 1]){
            child++;
        }

        if(elem[child] > elem[parent]){//判断是否需要调整
            int tmp = elem[parent];
            elem[parent] = elem[child];
            elem[child] = tmp;
            parent = child;//往下继续判断
            child = 2 * parent + 1;
        }else{
            break;
        }
    }
}

总代码

public class TestHeap {

    public int[] elem;
    public int usedSize;//有效的数据个数

    public static final int DEFAULT_SIZE = 10;

    public TestHeap() {
        elem = new int[DEFAULT_SIZE];
    }

    public void initElem(int[] array){
        for (int i = 0; i < array.length; i++) {
            elem[i] = array[i];
            usedSize++;
        }
    }

    public void creatHeap(){
        for (int parent = (usedSize - 1 - 1) / 2; parent >= 0; parent--) {
            //统一的调整方法
            shiftDown(parent,usedSize);
        }

    }

    /**
     *
     * @param parent 每颗子树的根节点
     * @param len  每颗子树调整的结束位置 不能大于 len
     */
    public void shiftDown(int parent,int len){
        int child = 2 * parent + 1;
        while(child < len){
            //判断孩子节点谁是最大的
            if(child + 1 < len && elem[child] < elem[child + 1]){
                child++;
            }

            if(elem[child] > elem[parent]){
                int tmp = elem[parent];
                elem[parent] = elem[child];
                elem[child] = tmp;
                parent = child;
                child = 2 * parent + 1;
            }else{
                break;
            }
        }
    }
}

这样子堆就创建好了，那创建堆的算法的复杂度该怎么算呢？接下来让我们来分析。

创建堆时间复杂度

假设树的高度为h，那么根节点需要调整的次数为h-1次，第二层节点需要调节的次数为h-2次…

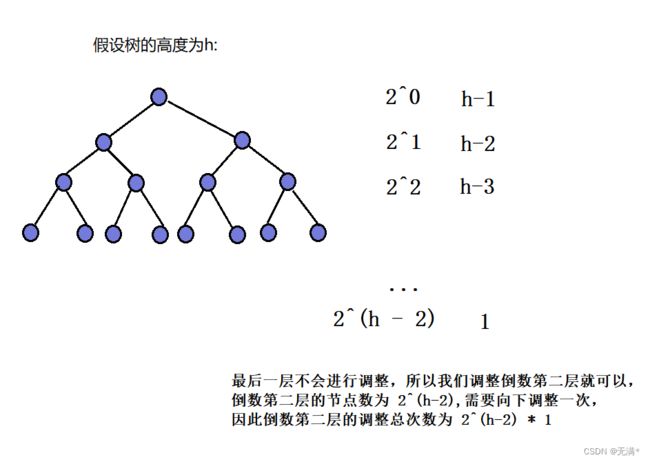
我们可以通过发现的规律得：创建堆最坏的情况下所需要的时间复杂度的计算公式。

错位相减得：T（n）= 2^h - 1 - h
因为 结点公式n = 2 ^ h - 1,所以可得 h = log（n + 1）
所以时间复杂度为：T（n）= n - log（n + 1）

堆的插入

接下来我们来对堆进行插入元素的操作。
思路：

1. 在插入的时候，先将元素放到堆的最底层空间，若空间不够就扩容
2. 再将插入后的新的堆进行调节，使它满足堆的特性。

比如插入元素10：

插入最底层的堆后，再对堆进行调整。

代码如下：

public void offer(int val){
    if(isFull()){
        //满了扩容
        elem = Arrays.copyOf(this.elem,2 * this.elem.length);
    }
    elem[usedSize] = val;
    usedSize++;
    //要重新调整为堆
    shiftUp(usedSize - 1);
}

public void shiftUp(int child){
 //再这个方法内向上调整
 int parent = (child - 1) / 2;
 while(child != 0 && elem[parent] < elem[child]){
     int tmp = elem[parent];
     elem[parent] = elem[child];
     elem[child] = tmp;
     child = parent;
     parent = (child - 1) / 2;
 }

堆的删除

删除堆顶元素
思路：

1. 我们可以将堆顶的元素与堆底的元素交换。
2. 然后再向下调节根节点为 0 的树。
3. 堆中的元素个数减少一个
   代码如下：

public boolean isFull(){
     return usedSize == elem.length;
 }
public int pop(){
   if(isEmpty()){//如果为null，返回-1
       return -1;
   }
   //将堆顶元素与最后一个元素交换，usedSize--；
   int tmp = elem[0];
   elem[0] = elem[usedSize - 1];
   elem[usedSize - 1] = tmp;
   usedSize--;

   //向下调整父亲节点为0 的树
   shiftDown(0,usedSize);
   return tmp;
}
public void shiftDown(int parent,int len){
    int child = 2 * parent + 1;
    while(child < len){
        //判断孩子节点谁是最大的
        if(child + 1 < len && elem[child] < elem[child + 1]){
            child++;
        }

        if(elem[child] > elem[parent]){
            int tmp = elem[parent];
            elem[parent] = elem[child];
            elem[child] = tmp;
            parent = child;
            child = 2 * parent + 1;
        }else{
            break;
        }
    }
}

这章就先将堆介绍到这里，下一章开始手撕PriorityQueue原码。