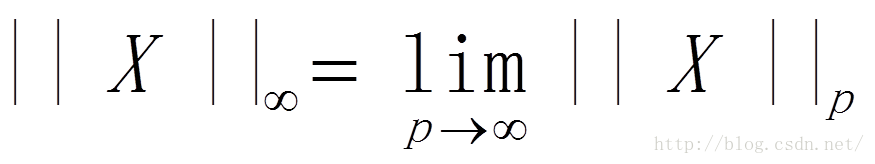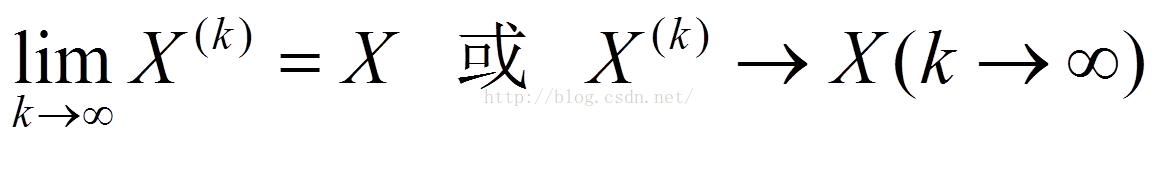什么是范数-学习
一、向量范数
对N维度的空间Rn中任意一个向量X,按照一定的法则,有一个确定的实数与之相对应,该实数记作║x║,如果║x║满足下面的三个性质,那么我们就称║x║为向量x的向量范数。
令x为向量:( x1,x2,…,xn)T
常用向量范数有4种
①1-范数:║x║1=│x1│+│x2│+…+│xn│②2-范数:║x║2=(│x1│^2+│x2│^2+…+│xn│^2)^1/2
③∞-范数:║x║∞=max(│x1│,│x2│,…,│xn│)
④p-范数:║x║p=(│x1│^p+│x2│^p+…+│xn│^p)^1/p
前三种范数都是p-范数的特殊情况,其中,
向量范数的连续性:
定理3.3 设f(X)=||X||为Rn上的任一向量范数,则f(X)为X的分量x1,x2,…,xn的连续函数
定理3.4 若||X||p与||X||q为Rn上任意两种范数,则存在C1,C2>0,使得对任意X∈Rn,都有:
C1||X||p≤ ||X||q ≤C2||X||p
注:同样有下列结论:存在C3,C4>0使得:
C3||X||q≤ ||X||p ≤C4||X||q
注:上述性质,称为向量范数的等价性。也就是说,Rn上任意两种范数都是等价的。在讨论向量序列的收敛性时要用到向量范数的等价性。
向量序列的收敛问题
定义:假定给定了Rn空间中的向量序列X(1),X(2),...,X(k),...,简记为{X(k)},其中X(k)=(x1(k),x2(k),...,xn(k))T,若X(k)的每一个分量xi(k)都存在极限xi,即
则称向量X= (x1,x2,...,xn)T为向量序列{X(k)}的极限,或者说向量序列{X(k)}收敛于向量X,记为
定理3.5 在空间Rn中,向量序列{X(k)}收敛于向量X的充要条件是对X的任意范数||·||,有:
二、矩阵范数
设A是n×n阶矩阵,A∈Rn×n
X∈Rn,||X||为Rn中的某数,称
为矩阵A的从属于该向量范数的范数,或称为矩阵A的算子,记为||A||。
设A是n×n矩阵,║A║是n维向量范数则
常用的三种向量范数诱导出的矩阵范数是
1-范数:║A║1= max{ ∑|ai1|, ∑|ai2| ,…… ,∑|ain| } (i=1,2,...n)(列范数,A每一列元素绝对值之和的最大值)
(其中∑|ai1|第一列元素绝对值的和∑|ai1|=|a11|+|a21|+...+|ann|,其余类似)
2-范数:║A║2=( max{ λi(ATA) } ) ^1/2 ( 谱范数,即ATA特征值λi中最大者λm的平方根,其中AT为A的转置矩阵).
∞-范数:║A║∞=max{ ∑|a1j|, ∑|a2j| ,..., ∑|ann| } (行范数,A每一行元素绝对值之和的最大值)
(其中为∑|a1j| 第一行元素绝对值的和,其余类似)
Frobenius范数: 它与向量2-范数相容.但非向量范数诱导出的矩阵范数.
F-范数:||A||F= ( ∑∑ aij^2 )^1/2 (F范数,A全部元素平方和的平方根)