数据结构4 - 树
树的常见问题:
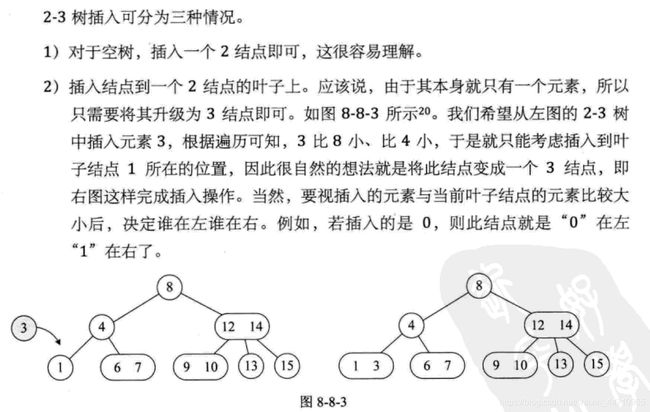
- B+树和B-树?
- 怎么求一个二叉树的深度?
- 二叉树层序遍历,要求每层打印出一个转行符。
- 二叉树任意两个结点之间路径的最大长度
- 如何打印二叉树每层的结点
1. 树的基本概念
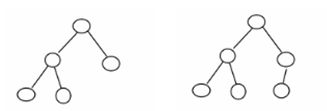
如图,(a)是一棵只有一个根节点的树,(b)是一棵只含一棵子树的树,©是一棵含有3棵子树的树
1.1 树的常用术语
1) 树的结点
树的结点是由一个数据元素及关联其子树的边所组成。
2) 结点的路径
结点的路径是指从根结点到该结点所经历的结点和分支的顺序排列。例如,图1.1©中结点J的路径是A→C→G→J
3)路径的长度
路径的长度是指结点路径中所包含的分支数。例如,图1.1©中结点J的路径长度为3.
4)结点的度
结点的度是指该结点所拥有子树的数目。例如,图1.1©中结点A的的度为3,B的度为1,C的度为2,结点I、O、P的度都为0。
5) 树的度
树的度是指树中所有结点的度的最大值。例如,图1.1(a)树的度为0,图1.1(b)树的度为1,图1.1©树的度为3。
6) 叶结点(终端结点)
叶结点是指树中度为0的结点,叶结点也称为终端结点。例如,图1. 1©中结点I、F、O、K、L、P、N都是叶结点。
7)分支结点(非终端结点)
分支结点是指树中度不为0的结点,分支结点也称为非终端结点。树中除叶结点之外的所有结点都是分支结点。
8)孩子结点(子结点)
一个结点的孩子结点是指这个结点的子树的根结点。例如,图1.1©中结点B、C、D是结点A的孩子结点,或者说结点A的孩子结点是B、C、D。
9)双亲结点(父结点)
一个结点的双亲结点是指:若树中某个结点有孩子结点,则这个结点就称为孩子结点的双亲结点。例如,图1.1©中结点A是结点B、C、D的双亲结点。双亲结点和孩子结点也称为是具有互为前驱和后继关系的结点,其中,双亲结点是孩子结点的前驱,而孩子结点是双亲结点的后继。
10)子孙结点
一个结点的子孙结点是指这个结点的所有子树中的任意结点。例如,图1. 1©中结点H的子孙结点有L、M、N、P结点。
11)祖先结点
一个结点的祖先结点是指该结点的路径中除此结点之外的所有结点。例如,图1.1©中结点P的祖先结点有A、D、H、M结点。
12)兄弟结点
兄弟结点是指具有同一双亲的结点。例如,图1. 1©中B、C、D是兄弟结点,它们的双亲都是结点A;L、M、N也是兄弟结点,它们的双亲都是结点H。
13) 结点的层次
规定树中根结点的层次为0,则其他结点的层次是其双亲结点的层次数加1。例如,图1.1©中结点P的层次数为4,也可称结点P在树中处于第4层上。
14)树的深度
树的深度是指树中所有结点的层次数的最大值加1。例如,图1.1(a)中树的深度为1,图1.1(b)中树的深度为3,图1. 1©中树的深度为5。
15) 有序树
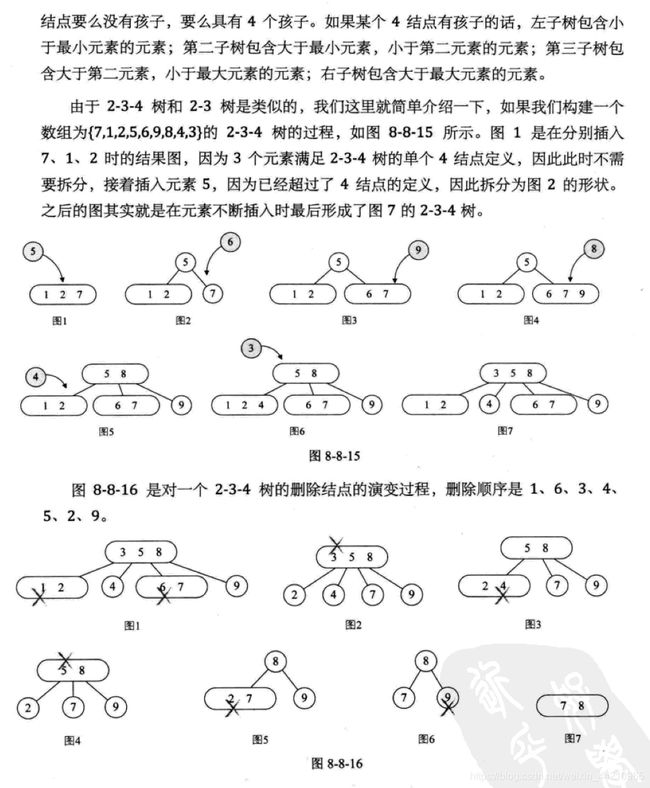
有序树是指树中各结点的所有子树之间从左到右有严格的次序关系,不能互换。也就是说,如果子树的次序不同则对应着不同的有序树。下图1.2所示的是两棵不同的二叉树,它们的不同点在于结点A的两棵子树的左右次序不相同。
2. 二叉树
2.1 二叉树的基本概念
2.1.1 树与二叉树的区别
1) 树中每个结点可以有多棵子树,二叉树最多有两课子树;
2) 树中的子树是不分顺序的,而二叉树有严格的左右之分;
3) 在树中,一个结点若是没有第一棵子树,则它不可能有第二棵子树的存在,而二叉树中允许某些结点只有右子树而没有左子树。
2.1.2 满二叉树
二叉树的一种特殊形态。满二叉树的所有结点都非空,并且所有叶节点都在同一层上。
2.1.3 完全二叉树
也是二叉树的一种特殊形态。如果在一棵具有n个结点的二叉树中,它的逻辑结构与满二叉树的前n个结点的逻辑结构相同,则称这样的二叉树为完全二叉树。
2.2 二叉树的性质
1) 二叉树中第i(i ≥ 0)层上的结点数最多为2i。
2) 深度为h(h ≥ 1)的二叉树中最多有2h - 1个结点。
3) 对于任意一棵二叉树,其叶结点的个数为n0,度为2的结点个数为n2,则有n0 = n2 + 1。
4) 具有n个结点的完全二叉树,其深度为[log2n] + 1或者[log2(n + 1)]。
5) 对于具有n个结点的完全二叉树,若从根结点开始自上而下并且按照层次由左向右对结点从0开始进行编号,则对于任意一个编号为i(0 <= i < n)的结点有:
a) 若i = 0,则编号为i的结点是二叉树的根结点,它没有双亲;若i > 1,则编号为i的结点其双亲的编号为[(i - 1) / 2]。
b)若2i + 1 ≥ n,则编号为i的结点无左孩子,否则编号为2i + 1的结点就是其左孩子。
c)若2i + 2 ≥ n,则编号为i的结点无右孩子,否则编号为2i+2的结点就是其右孩子。
2.3 二叉树的存储结构
2.3.1 二叉树的顺序存储结构
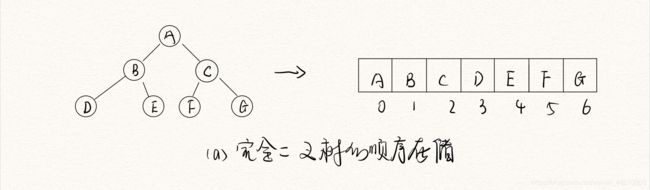
顺序存储方式非常适用于满二叉树和完全二叉树。但是对于非完全二叉树,由于“虚结点”的存在从而造成存储空间的浪费。
顺序存储二叉树的特点:
- 顺序二叉树通常只考虑完全二叉树
- 第 n 个元素的左子节点为 2n + 1
- 第 n 个元素的右子节点为 2n + 2
- 第 n 个元素的父节点为 (n - 1) / 2
n : 表示二叉树中的第几个元素(按 0 开始编号,如图所示)
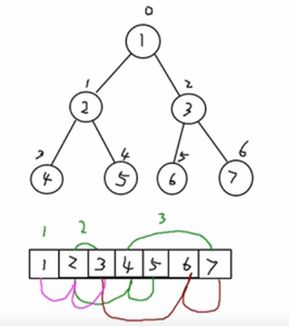
练习:
给你一个数组 {1,2,3,4,5,6,7},要求以二叉树前序遍历(先根遍历)的方式进行遍历。 前序遍历的结果应当为 1,2,4,5,3,6,7。
public class ArrayBinaryTreeDemo {
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5, 6, 7};
preOrder(arr, 0); //1 2 4 5 3 6 7
System.out.println();
inOrder(arr, 0); //4 2 5 1 6 3 7
System.out.println();
postOrder(arr, 0); //4 5 2 6 7 3 1
}
//前序遍历
public static void preOrder(int[] arr,int index) {
if (arr == null || arr.length == 0)
System.out.print("数组为空,不能按照二叉树前序遍历");
System.out.print(arr[index]+" ");
if ((index * 2 + 1) < arr.length)
preOrder(arr,index * 2 + 1);
if ((index * 2 + 2) < arr.length)
preOrder(arr,index * 2 + 2);
}
//中序遍历
public static void inOrder(int[] arr,int index) {
if (arr == null || arr.length == 0)
System.out.print("数组为空,不能按照二叉树中序遍历");
if ((index * 2 + 1) < arr.length)
inOrder(arr,index * 2 + 1);
System.out.print(arr[index]+" ");
if ((index * 2 + 2) < arr.length)
inOrder(arr,index * 2 + 2);
}
//后序遍历
public static void postOrder(int[] arr,int index) {
if (arr == null || arr.length == 0)
System.out.print("数组为空,不能按照二叉树中序遍历");
if ((index * 2 + 1) < arr.length)
postOrder(arr,index * 2 + 1);
if ((index * 2 + 2) < arr.length)
postOrder(arr,index * 2 + 2);
System.out.print(arr[index]+" ");
}
}
2.3.2 二叉树的链式存储结构
用链式存储方式来实现二叉树的存储时,可以有两种方式,二叉链表存储结构和三叉链表存储结构。

二叉链式存储结构的结点描述:
public class BiTreeNode {
public Object data;
public BiTreeNode lchild,rchild;
//构造一个结点
public BiTreeNode(){
this(null);
}
//构造一个左、右孩子域为空的二叉树
public BiTreeNode(Object data){
this(data,null,null);
}
//构造一棵数据域和孩子域都不为空的二叉树
public BiTreeNode(Object data, BiTreeNode lchild, BiTreeNode rchild){
this.data = data;
this.lchild = lchild;
this.rchild = rchild;
}
}
2.4 二叉树的遍历
1) 层次遍历
若二叉树为空,则为空操作;否则,先访问第0层的根节点,然后从左到右依次访问第1层的每一个结点…依次类推…
2) 先根遍历(DLR,前序遍历)
若二叉树为空,则为空操作;否则
a)访问根结点
b)先根遍历左子树
c)先根遍历右子树
3) 中根遍历(LDR,中序遍历)
若二叉树为空,则为空操作;否则
a)中根遍历左子树
b)访问根结点
c)中根遍历右子树
4) 后根遍历(LRD,后序遍历)
若二叉树为空,则为空操作;否则
a)后根遍历左子树
b)后根遍历右子树
c)访问根结点
如图2.3(a),层次遍历为ABCDEFGH;先根遍历为ABDEGCFH;中根遍历为DBGEAFHC;后根遍历为DGEBHFCA
2.5 建立二叉树
先根遍历序列或后根遍历序列能反映双亲与孩子结点之间的层次关系,而中根遍历序列能反映兄弟结点之间的左右次序关系。所以已知先根和中根遍历序列,或中根和后根遍历序列,才能唯一确认一棵二叉树。而已知先根和后根遍历序列也无法确认一棵二叉树。
1) 由先根和中根遍历序列建立一棵二叉树
要实现上述建立二叉树的算法,需要引入5个参数:
- preOrder:整棵树的先根遍历序列
- inOrder:整棵树的中根遍历序列
- preIndex:先根遍历序列在preOrder中开始的位置
- inIndex:中根遍历序列在inOrder中开始的位置
- count:树中结点的个数
/**
* 由先根遍历和中根遍历序列创建一棵二叉树的算法
* */
public BiTree(String preOrder, String inOrder, int preIndex, int inIndex, int count){
if(count > 0){ //先根和中根非空
char r = preOrder.charAt(preIndex); //取先根遍历序列中的第一个结点作为根结点
int i = 0;
for(; i < count; i++) //寻找根结点在中根遍历序列中的位置
if(r == inOrder.charAt(i + inIndex))
break;
root = new BiTreeNode(r); //建立树的根结点
root.lchild = new BiTree(preOrder, inOrder, preIndex + 1, inIndex, i).root; //建立树的左子树
root.rchild = new BiTree(preOrder, inOrder, preIndex + i + 1, inIndex + i + 1, count - i - 1).root; //建立树的右子树
}
}
2) 由标明空子树的先根遍历序列建立一棵二叉树
/**
* 由标明空子树的先根遍历序列创建一棵二叉树,并返回其根结点
* */
private static int index = 0; //用于记录preStr的索引值
public BiTree(String preStr){
char c = preStr.charAt(index++); //取出字符串索引为index的字符,且index增1
if(c != '#'){ //字符不为#
root = new BiTreeNode(c); //建立树的根结点
root.lchild = new BiTree(preStr).root; //建立树的左子树
root.rchild = new BiTree(preStr).root; //建立树的右子树
}else
root = null;
}
Test:
/**
* 由先根和中根遍历序列建立一棵二叉树,并输出该二叉树的后根遍历序列
* */
String preOrder = "ABDEGCFH";
String inOrder = "DBGEAFHC";
BiTree biTree = new BiTree(preOrder, inOrder, 0, 0, preOrder.length());
System.out.print("后根遍历:");
biTree.postRootTraverse(); // DGEBHFCA
System.out.println();
/**
* 首先由标明空子树的先根遍历序列创建一棵二叉树,然后标出该二叉树的先根、中根、后根遍历序列
* */
String preStr = "AB##CD###";
BiTree T = new BiTree(preStr);
System.out.print("先根遍历:");
T.preRootTraverse(); //ABCD
System.out.println();
System.out.print("中根遍历:");
T.inRootTraverse(); //BADC
System.out.println();
System.out.print("后根遍历:");
T.postRootTraverse(); //BDCA
2.6 二叉树常见方法 - 二叉链式存储结构
public class BiTree {
public BiTreeNode root; //树的根结点
//构造一棵空树
public BiTree(){
this.root = null;
}
//构造一棵树
public BiTree(BiTreeNode root){
this.root = root;
}
/**
* 由先根遍历和中根遍历序列创建一棵二叉树的算法
* */
public BiTree(String preOrder, String inOrder, int preIndex, int inIndex, int count){
if(count > 0){ //先根和中根非空
char r = preOrder.charAt(preIndex); //取先根遍历序列中的第一个结点作为根结点
int i = 0;
for(; i < count; i++) //寻找根结点在中根遍历序列中的位置
if(r == inOrder.charAt(i + inIndex))
break;
root = new BiTreeNode(r); //建立树的根结点
root.lchild = new BiTree(preOrder, inOrder, preIndex + 1, inIndex, i).root; //建立树的左子树
root.rchild = new BiTree(preOrder, inOrder, preIndex + i + 1, inIndex + i + 1, count - i - 1).root; //建立树的右子树
}
}
/**
* 由标明空子树的先根遍历序列创建一棵二叉树,并返回其根结点
* */
private static int index = 0; //用于记录preStr的索引值
public BiTree(String preStr){
char c = preStr.charAt(index++); //取出字符串索引为index的字符,且index增1
if(c != '#'){ //字符不为#
root = new BiTreeNode(c); //建立树的根结点
root.lchild = new BiTree(preStr).root; //建立树的左子树
root.rchild = new BiTree(preStr).root; //建立树的右子树
}else
root = null;
}
/**
* 先根遍历二叉树的递归算法
* */
public void preRootTraverse(BiTreeNode T){
if(T != null){
System.out.print(T.data); //访问根结点
preRootTraverse(T.lchild); //先根遍历左子树
preRootTraverse(T.rchild); //先根遍历右子树
}
}
/**
* 先根遍历二叉树的非递归算法
* 1)创建一个栈对象,根结点入栈
* 2)当栈为非空时,将栈顶结点弹出栈内并访问该结点。
* 3)对当前访问结点的非空左孩子结点相继依次访问,并将当前访问结点的非空右孩子结点压入栈内。
* 4)重复2)和3),直到栈为空
* */
public void preRootTraverse() throws Exception {
BiTreeNode T = root;
if(T != null){
LinkStack S = new LinkStack();
S.push(T);
while (!S.isEmpty()){
T = (BiTreeNode) S.pop();
System.out.print(T.data);
while (T != null){
if(T.lchild != null)
System.out.print(T.lchild.data);
if(T.rchild != null)
S.push(T.rchild);
T = T.lchild;
}
}
}
}
/**
* 中根遍历二叉树的递归算法
* */
public void inRootTraverse(BiTreeNode T){
if(T != null){
inRootTraverse(T.lchild);
System.out.print(T.data);
inRootTraverse(T.rchild);
}
}
/**
* 中根遍历二叉树的非递归算法
*
* 1)创建一个栈对象,根结点入栈
* 2)若栈非空,则将栈顶结点的左孩子相继入栈
* 3)栈顶结点出栈,并将该结点的右孩子入栈
* 4)重复2)和3),直到栈为空
* */
public void inRootTraverse() throws Exception {
BiTreeNode T = root;
if(T != null){
LinkStack S = new LinkStack();
S.push(T); //根结点入栈
while (!S.isEmpty()){
while(S.peek() != null) //将栈顶结点的左结点相继入栈
S.push(((BiTreeNode)S.peek()).lchild);
S.pop(); //空结点退栈
if(!S.isEmpty()){
T = (BiTreeNode) S.pop();
System.out.print(T.data);
S.push(T.rchild); //结点的右孩子入栈
}
}
}
}
/**
* 后根遍历二叉树的递归算法
* */
public void postRootTraverse(BiTreeNode T){
if(T != null){
postRootTraverse(T.lchild);
postRootTraverse(T.rchild);
System.out.print(T.data);
}
}
/**
* 后根遍历二叉树的非递归算法
*
* (1)创建一个栈对象,根结点进栈,p赋初始值null。
* (2)若栈非空,则栈顶结点的非空左孩子相继进栈。
* (3)若栈非空,查看栈顶结点,若栈顶结点的右孩子为空,或者与p相等,则将栈顶结点弹出栈并访问它,
* 同时使p指向该结点,并置flag 值为true;否则,将栈顶结点的右孩子压入栈,并置flag值为false。
* (4)若flag值为true,则重复执行步骤(3);否则,重复执行步骤(2)和(3),直到栈为空为止。
* */
public void postRootTraverse() throws Exception {
BiTreeNode T = root;
if(T != null){
LinkStack S = new LinkStack();
S.push(T);
Boolean flag; //访问标记
BiTreeNode p = null; //p指向刚刚被访问过的结点
while(!S.isEmpty()){
while (S.peek() != null) //将栈顶结点的左结点相继入栈
S.push(((BiTreeNode)S.peek()).lchild);
S.pop(); //空结点退栈
while (!S.isEmpty()){
T = (BiTreeNode) S.peek(); //查看栈顶元素
if(T.rchild == null || T.rchild == p){
System.out.print(T.data);
S.pop();
p = T; //p指向刚刚被访问过的结点
flag = true; //设置访问标记
}else{
S.push(T.rchild);
flag = false; //设置未访问标记
}
if(!flag)
//当flag = true时,说明元素都已经入栈完毕,可以继续出栈
//当flag = false时,说明栈顶元素是刚刚进来的右结点,所以退出循环把该结点的左结点压入栈顶
break;
}
}
}
}
/**
* 层次遍历二叉树的算法(自左向右)
* */
public void levelRootTraverse() throws Exception {
BiTreeNode T = root;
if(T != null){
LinkQueue L = new LinkQueue();
L.offer(T);
while (!L.isEmpty()){
T = (BiTreeNode) L.poll();
System.out.print(T.data);
if(T.lchild != null)
L.offer(T.lchild);
if(T.rchild != null)
L.offer(T.rchild);
}
}
}
public BiTreeNode getRoot(){
return root;
}
public void setRoot(BiTreeNode root){
this.root = root;
}
/**
* 在二叉树中查找值为x的结点,若找到则返回该值,否则返回空值
* */
public BiTreeNode searchNode(BiTreeNode T, Object x){
if(T != null){
if(T.data.equals(x))
return T;
else {
BiTreeNode lresult = searchNode(T.lchild, x);
return lresult != null ? lresult : searchNode(T.rchild, x);
}
}
return null;
}
/**
* 统计二叉树中结点个数的算法
* */
public int countNode(BiTreeNode T){
//采用先根遍历的方式对二叉树进行遍历,计算其结点的个数
int count = 0;
if(T != null){
++ count;
count += countNode(T.lchild);
count += countNode(T.rchild);
}
return count;
}
/**
* 统计二叉树中结点个数的算法 -- 递归
* */
public int countNode1(BiTreeNode T){
if(T == null)
return 0;
else
return countNode1(T.lchild) + countNode1(T.rchild) + 1;
}
/**
* 求二叉树的深度
* */
public int getDepth(BiTreeNode T){
if(T != null){
int lDepth = getDepth(T.lchild);
int rDepth = getDepth(T.rchild);
return 1 + (lDepth > rDepth ? lDepth : rDepth);
}
return 0;
}
/**
* 求二叉树的深度 -- 递归
* */
public int getDepth1(BiTreeNode T){
if(T == null)
return 0;
else if(T.lchild == null && T.rchild == null)
return 1;
else
return 1 + (getDepth1(T.lchild) > getDepth1(T.rchild) ? getDepth1(T.lchild) : getDepth1(T.rchild));
}
/**
* 判断两棵二叉树是否相等
* */
public boolean isEqual(BiTreeNode T1, BiTreeNode T2){
if(T1 == null && T2 == null)
return true;
if(T1 != null && T2 != null)
if(T1.data.equals( T2.data))
if(isEqual(T1.lchild, T2.lchild));
if(isEqual(T1.rchild, T2.rchild))
return true;
return false;
}
/**
* 判断两棵二叉树是否相等 -- 递归模型
* */
public boolean isEqual1(BiTreeNode T1, BiTreeNode T2){
if(T1 == null && T2 == null)
return true;
else if(T1 != null && T2 != null)
return (T1.data.equals(T2.data)) && (isEqual1(T1.lchild, T2.lchild)) && (isEqual1(T1.rchild, T2.rchild));
else
return false;
}
}
Test:
public class Test {
public static void main(String[] args) throws Exception {
Test test = new Test();
BiTree biTree = test.creatBitree();
BiTreeNode root = biTree.root; //取得树的根结点
//调试先根遍历
System.out.print("(递归)先根遍历为:");
biTree.preRootTraverse(root);
System.out.println();
System.out.print("(非递归)先根遍历为:");
biTree.preRootTraverse();
System.out.println();
//调试中根遍历
System.out.print("(递归)中根遍历为:");
biTree.inRootTraverse(root);
System.out.println();
System.out.print("(非递归)中根遍历为:");
biTree.inRootTraverse();
System.out.println();
//调试后根遍历
System.out.print("(递归)后根遍历为:");
biTree.postRootTraverse(root);
System.out.println();
System.out.print("(非递归)后根遍历为:");
biTree.postRootTraverse();
System.out.println();
//调试层次遍历
System.out.print("层次遍历为:");
biTree.levelRootTraverse();
System.out.println();
System.out.println();
}
//构建如图2.3(a)的二叉树
public BiTree creatBitree(){
BiTreeNode d = new BiTreeNode('D');
BiTreeNode g = new BiTreeNode('G');
BiTreeNode h = new BiTreeNode('H');
BiTreeNode e = new BiTreeNode('E',g,null);
BiTreeNode b = new BiTreeNode('B',d,e);
BiTreeNode f = new BiTreeNode('F',null,h);
BiTreeNode c = new BiTreeNode('C',f,null);
BiTreeNode a = new BiTreeNode('A',b,c);
return new BiTree(a);
}
}
2.7 线索化二叉树
2.7.1 线索二叉树基本介绍
- n 个结点的二叉链表中含有 n+1 【公式 2n - (n - 1) = n + 1】 个空指针域。利用二叉链表中的空指针域,存放指向该结点在某种遍历次序下的前驱和后继结点的指针(这种附加的指针称为"线索")。
- 这种加上了线索的二叉链表称为线索链表,相应的二叉树称为线索二叉树(Threaded BinaryTree)。根据线索性质的不同,线索二叉树可分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种。
2.7.2 线索二叉树应用案例
思路分析: 中序遍历的结果:{8, 3, 10, 1, 14, 6}
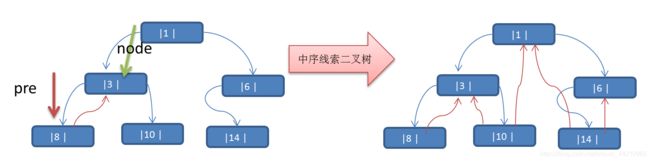
说明: 当线索化二叉树后,Node节点的属性 left 和 right ,有如下情况:
- left 指向的是左子树,也可能是指向的前驱节点, 比如 ① 节点 left 指向的左子树, 而 ⑩ 节点的 left 指向的就是前驱节点。
- right指向的是右子树,也可能是指向后继节点,比如 ① 节点right 指向的是右子树,而⑩ 节点的right 指向的是后继节点。
线索化二叉树的结点类:
public class BiTreeNode {
public Object data;
public BiTreeNode lchild,rchild;
//线索化二叉树
//leftType如果是0,则表示指向左子树,是1指向前驱结点
public int leftType, rightType;
//构造一个结点
public BiTreeNode(){
this(null);
}
//构造一个左、右孩子域为空的二叉树
public BiTreeNode(Object data){
this(data,null,null);
}
//构造一棵数据域和孩子域都不为空的二叉树
public BiTreeNode(Object data, BiTreeNode lchild, BiTreeNode rchild){
this.data = data;
this.lchild = lchild;
this.rchild = rchild;
}
}
二叉链式存储结构下二叉树类的描述 :
public class BiTree {
public BiTreeNode root; //树的根结点
//为了实现线索化,需要创建指向当前结点的前驱结点的指针
//在递归进行线索化时,pre总是保留前一个结点
public BiTreeNode pre = null;
//可以重载一下下面线索化的方法,如果嫌传参数麻烦的话
public void threadedNodes(){
this.threadedNodes(root);
}
/**
* 线索化二叉树
*
* T 为当前需要线索化的结点
* */
public void threadedNodes(BiTreeNode T){
if(T == null)
return;
//1. 线索化左子树
threadedNodes(T.lchild);
//2. 线索化当前结点
//处理当前结点的前驱结点
if(T.lchild == null){
T.lchild = pre;
T.leftType = 1; //修改当前结点的左指针的类型,指向当前前驱
}
//处理当前结点的后继结点
if(pre != null && pre.rchild == null){
pre.rchild = T; //让前驱结点的右指针指向当前结点
pre.rightType = 1;
}
//!!每处理一个结点后,让当前结点是下一个结点的前驱结点
pre = T;
//3. 线索化右子树
threadedNodes(T.rchild);
}
/**
* 遍历线索化二叉树的方法
* */
public void threadedList(){
//定义一个变量,存储当前遍历的结点,从root开始
BiTreeNode node = root;
while (node != null){
//循环找到leftType == 1 的结点
//处理后的有效结点
while (node.leftType == 0)
node = node.lchild;
//打印这个结点
System.out.print(node.data + " ");
//如果当前结点的右指针指向的是后继结点,就一直输出
while(node.rightType == 1){
//获取到当前结点的后继结点
node = node.rchild;
System.out.print(node.data + " ");
}
//替换这个遍历的结点
node = node.rchild;
}
}
....
}
Test:
//中序遍历的结果:{8, 3, 10, 1, 14, 6}
public static void main(String[] args) throws Exception {
BiTreeNode node8 = new BiTreeNode(8);
BiTreeNode node10 = new BiTreeNode(10);
BiTreeNode node14 = new BiTreeNode(14);
BiTreeNode node3 = new BiTreeNode(3,node8,node10);
BiTreeNode node6 = new BiTreeNode(6,node14,null);
BiTreeNode node1 = new BiTreeNode(1,node3,node6);
BiTree biTree = new BiTree(node1);
// biTree.preRootTraverse(note1);
//测试中序线索化
biTree.threadedNodes();
//测试:以10号结点测试
BiTreeNode leftNode = node10.lchild;
System.out.println("10号结点的前驱是:"+leftNode.data);//3
BiTreeNode rightNode = node10.rchild;
System.out.println("10号结点的后继是:"+rightNode.data);//1
//线索化二叉树的遍历
biTree.threadedList(); //8 3 10 1 14 6
}
2.7.3 线索二叉树的遍历
(算法如上述代码所示)
3. 哈夫曼树
(哈夫曼树不唯一,哈夫曼编码也不唯一)
3.1 哈夫曼树的基本概念
1) 结点间的路径和结点的路径长度
结点间的路径时指从一个结点到另一个结点所经历的结点和分支序列。
结点的路径长度是指从根结点到该结点间的路径上的分支数目。
2)结点的权和结点的带权路径长度
在实际应用中,人们往往会给树中的每一个结点赋予一个某种实际意义的数值,这个数值称为该结点的权值。
结点的带权路径长度就是该结点的路径长度与该结点的权值的乘积。
3)树的带权路径长度
树的带权路径长度就是树中所有叶结点的带权路径长度之和,通常记为:
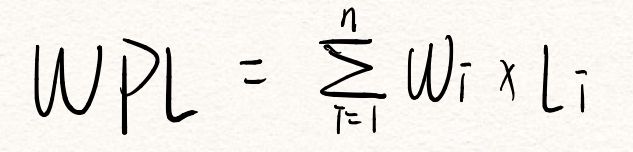
其中,n为叶结点的个数,Wi为第i个叶结点的权值,Li为第i叶结点的路径长度。
4)最优二叉树
给定n个权值并作为n个叶结点按一定规则构造一棵二叉树,使其带权路径长度达到最小值,则这棵二叉树称为最优二叉树,也称为哈夫曼树。
3.2 哈夫曼树和哈夫曼编码的构造方法
3.2.1 构造哈夫曼树算法的主要步骤:
假设n个叶结点的权值分别为(W1,W2,…,Wn},则
(1) 由已知给定的n个权值(W1,W2,…,Wn},构造一个由n棵二叉树所构成的森林 F = {T1,T2,…,Tn},其中每一棵二叉树只有一个根结点,并且根结点的权值分别为W1,W2,…,Wn。
(2) 在二叉树森林 F 中选取根结点的权值最小和次小的两棵二叉树,分别把它们作为左子树和右子树去构造一棵新二叉树,新二叉树的根结点权值为其左、右子树根结点的权值之和。
(3) 作为新二叉树的左、右子树的两棵二叉树从森林 F 中删除,将新产生的二叉树加入到森林 F 中。
(4) 重复步骤(2)和(3),直到森林中只剩下一棵二叉树为止,则这棵二叉树就是所构造成的哈夫曼树。
3.2.2 用哈夫曼树进行编码
哈夫曼构造编码的过程:用电文中各个字符使用的频度作为叶结点的权,构造一棵具有最小带权路径长度的哈夫曼树,若对树中的每个左分支赋予标记0,右分支赋予标记1,则从根结点到每个叶结点的路径上的标记连接起来就构成一个二进制串,该二进制串被称为哈夫曼编码。
3.2.3 用哈夫曼树进行译码
从哈夫曼树的根开始,从左到右把二进制编码的每一位进行判别,若遇到0,则选择左分支走向下一个结点;若遇到1,则选择右分支走向下一个结点,直至到达一个树叶结点。因为信息中出现的字符在哈夫曼树中是叶结点,所以确定了一条从根到树叶的路径,就意味着译出了一个字符,然后继续用这棵哈夫曼树并用同样的方法去译出其他的二进制编码。如图3.3(b)所示,对于编码为0110的译码过程就是从根开始的,先左、再右、再右、再左,最后到达使用频度为6的字符g,这个过程如图3.3(b)中的箭头所示。
4. 二叉排序树(BST)
4.1 二叉排序树的定义
二叉排序树(Binary Sort Tree)或者是一棵空树,或者是一颗具有下列性质的二叉树:
(1) 若左子树不空,则左子树上所有结点的值均小于根结点的值。
(2) 若右子树不空,则右子树上所有结点的值均大于根结点的值。
(3) 它的左右子树也都是二叉排序树。
特殊说明:如果有相同的值,可以将结点放在左子结点或右子结点。
比如针对数据 (7, 3, 10, 12, 5, 1, 9) ,对应的二叉排序树为:
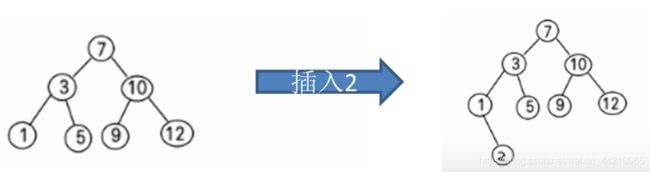
4.2 二叉排序树的创建和遍历
/**
* @author liyingdan
* @date 2019/10/20
*
* 二叉排序树
*/
public class BSTree {
public BSTNode root;
public BSTree(){
root = null;
}
//中根遍历以p结点为根的二叉树
public void inOrderTraverse(BSTNode p){
if(p != null){
inOrderTraverse(p.lchild);
System.out.print(p.data+" ");
inOrderTraverse(p.rchild);
}
}
//添加结点的方法
public Boolean insertBST(BSTNode node){
if(node == null)
return false;
if(root == null){
root = node;
return true;
}
return insertBST(node,root);
}
public Boolean insertBST(BSTNode node, BSTNode p){
if(node.data < p.data){
if(p.lchild == null){
p.lchild = node;
return true;
}
else
return insertBST(node,p.lchild);
} else{
if(p.rchild == null){
p.rchild = node;
return true;
}
else
return insertBST(node,p.rchild);
}
}
//-------------------------------------------------------
//查找要删除的结点的方法
/**
* @param data 要查找的值
* @param p 当前结点
* @return 要删除的结点
* */
public BSTNode search(int data, BSTNode p){ //data为要删除结点的值
if(p != null){
if(data == p.data)
return p;
else if(data < p.data) //值小于当前结点
return search(data, p.lchild);
else //值不小于当前结点,向右子树递归查找
return search(data, p.rchild);
}
return null;
}
//查找要删除结点的父结点
/**
* @param data 要查找的值
* @param p 当前结点
* @return 要删除的结点的父结点
* */
public BSTNode searchParent(int data, BSTNode p){
if(p != null){
if((p.lchild != null && p.lchild.data == data) || (p.rchild != null && p.rchild.data == data))
return p;
else{
if(data < p.data)
return searchParent(data,p.lchild);
else if(data >= p.data)
return searchParent(data,p.rchild);
else
return null; //没有找到父结点
}
}
return null;
}
//返回以node为根结点的二叉排序树的最小结点的值,并且删除此最小结点
public int delRightTreeMin(BSTNode node){
BSTNode target = node;
while (target.lchild != null)
target = target.lchild;
removeBST(target.data);
return target.data;
}
/**
* 二叉排序树结点的删除
* */
public void removeBST(int data){
if(root == null)
return;
else{
//1. 先找到要删除的结点
BSTNode targetNode = search(data, root);
if(targetNode == null)
return;
if(root.lchild == null && root.rchild == null){ //要删除的结点刚好的根结点
root = null;
return;
}
//2. 找到targetNode的父结点
BSTNode parent = searchParent(data, root);
//3. 如果要删除的是叶子结点
if(targetNode.lchild == null && targetNode.rchild == null){
//判断targetNode是父结点的左结点还是右结点
if(parent.lchild != null && parent.lchild.data == data)
parent.lchild = null;
else if(parent.rchild != null && parent.rchild.data == data)
parent.rchild = null;
//4. 删除有两课子树的结点
}else if(targetNode.lchild != null && targetNode.rchild != null){
int minVal = delRightTreeMin(targetNode.rchild);
targetNode.data = minVal;
//5. 删除只有一棵子树的结点
}else {
if(targetNode.lchild != null){ //如果要删除的结点有左子节点
if(parent != null){
if(parent.lchild.data == data)
parent.lchild = targetNode.lchild;
else
parent.rchild = targetNode.lchild;
}else
root = targetNode.lchild;
}else{ //如果要删除的结点有右子结点
if(parent != null){
if(parent.lchild.data == data)
parent.lchild = targetNode.rchild;
else
parent.rchild = targetNode.rchild;
}else
root = targetNode.rchild;
}
}
}
}
}
Test:
public class Test {
public static void main(String[] args) {
int[] arr = {7,3,10,12,5,1,9,0};
BSTree bsTree = new BSTree();
for (int i = 0; i < arr.length; i++) {
bsTree.insertBST(new BSTNode(arr[i]));
}
bsTree.inOrderTraverse(bsTree.root); //0 1 3 5 7 9 10 12
bsTree.removeBST(10);
System.out.println("删除结点后");
bsTree.inOrderTraverse(bsTree.root); //0 1 3 5 7 9 12
}
}
4.3 二叉排序树的删除
二叉排序树的删除有三种情况:
1)删除叶子结点(比如2,5,9,12):直接删除即可。
2)删除只有一棵子树的结点(比如1):可以将其子树代替删除的位置。
3)删除有两课子树的结点(比如7,3,10):可用被删除结点在中序遍历下的前驱结点或后继结点代替被删除结点。
代码如上。
5. 平衡二叉树(AVL)
5.1 基本介绍
1)平衡二叉树也叫平衡二叉搜索树(Self-balancing binary search tree),又被称为AVL树, 可以保证查询效率较高。
2)具有以下特点:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。
5.2 AVL树的创建
/**
* @author liyingdan
* @date 2019/10/23
*
* 引用BSTNode结点
*/
public class AVLTree {
public BSTNode root;
public AVLTree(){
root = null;
}
//返回当前结点的高度,以该结点为根结点的树的高度
public int getHeight(BSTNode p){
if(p != null)
return Math.max(getHeight(p.lchild),getHeight(p.rchild)) + 1;
return 0;
}
//返回左子树的高度
public int leftHeight(BSTNode p){
if(p != null){
if(p.lchild == null)
return 0;
else
return getHeight(p.lchild);
}
return 0;
}
//返回右子树的高度
public int rightHeight(BSTNode p){
if(p != null){
if(p.rchild == null)
return 0;
else
return getHeight(p.rchild);
}
return 0;
}
/**
* 左旋转的方法
* */
public void leftRotate(BSTNode p){
BSTNode newNode = new BSTNode(p.data); //创建新的结点,以当前根结点的值
newNode.lchild = p.lchild; //新的结点的左子树为当前根结点的左子树
newNode.rchild = p.rchild.lchild; //新的结点的右子树为当前根结点的右子树的左子树
p.data = p.rchild.data; //把当前根结点的值替换成该右子结点的值
p.rchild = p.rchild.rchild; //当前根结点的右子树为它右子树的右子树
p.lchild = newNode; //当前根结点的左子树为新创建的结点
}
/**
* 右旋转
* */
public void rightRotate(BSTNode p){
BSTNode newNode = new BSTNode(p.data);
newNode.rchild = p.rchild;
newNode.lchild = p.lchild.rchild;
p.data = p.lchild.data;
p.lchild = p.lchild.lchild;
p.rchild = newNode;
}
/*---------------------------------------------------*/
//中根遍历以p结点为根的二叉树
public void inOrderTraverse(BSTNode p){
if(p != null){
inOrderTraverse(p.lchild);
System.out.print(p.data+" ");
inOrderTraverse(p.rchild);
}
}
//添加结点的方法
public void insertAVL(BSTNode node){
if(node == null)
return;
if(root == null){
root = node;
return;
}
insertAVL(node,root);
//当添加完一个结点后,如果:(右子树的高度 - 左子树的高度)> 1 ,左旋转
if(rightHeight(root) - leftHeight(root) > 1){
if(root.rchild != null && leftHeight(root.rchild) > rightHeight(root.rchild)){
rightRotate(root.rchild);
leftRotate(root);
}else
leftRotate(root);
return;
}
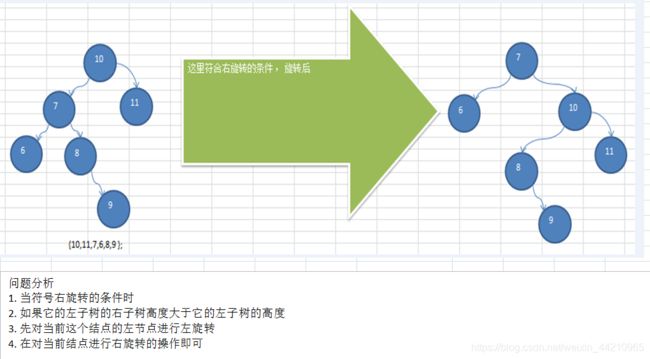
//当添加完一个结点后,如果:(左子树的高度 - 右子树的高度)> 1 ,右旋转
if(leftHeight(root) - rightHeight(root) > 1){
//如果它的左子树的右子树高度大于它的左子树高度
if(root.lchild != null && rightHeight(root.lchild) > leftHeight(root.lchild)){
leftRotate(root.lchild); //先对当前结点的左结点(左子树)-->左旋转
rightRotate(root); //再对当前结点进行右旋转
}else
rightRotate(root); //直接右旋转即可
}
}
public void insertAVL(BSTNode node, BSTNode p){
if(node.data < p.data){
if(p.lchild == null){
p.lchild = node;
}
else
insertAVL(node,p.lchild);
} else{
if(p.rchild == null){
p.rchild = node;
}
else
insertAVL(node,p.rchild);
}
}
//查找要删除的结点的方法
/**
* @param data 要查找的值
* @param p 当前结点
* @return 要删除的结点
* */
public BSTNode search(int data, BSTNode p){ //data为要删除结点的值
if(p != null){
if(data == p.data)
return p;
else if(data < p.data) //值小于当前结点
return search(data, p.lchild);
else //值不小于当前结点,向右子树递归查找
return search(data, p.rchild);
}
return null;
}
//查找要删除结点的父结点
/**
* @param data 要查找的值
* @param p 当前结点
* @return 要删除的结点的父结点
* */
public BSTNode searchParent(int data, BSTNode p){
if(p != null){
if((p.lchild != null && p.lchild.data == data) || (p.rchild != null && p.rchild.data == data))
return p;
else{
if(data < p.data)
return searchParent(data,p.lchild);
else if(data >= p.data)
return searchParent(data,p.rchild);
else
return null; //没有找到父结点
}
}
return null;
}
//返回以node为根结点的平衡二叉树的最小结点的值,并且删除此最小结点
public int delRightTreeMin(BSTNode node){
BSTNode target = node;
while (target.lchild != null)
target = target.lchild;
removeAVL(target.data);
return target.data;
}
/**
* 平衡二叉树结点的删除
* */
public void removeAVL(int data){
if(root == null)
return;
else{
//1. 先找到要删除的结点
BSTNode targetNode = search(data, root);
if(targetNode == null)
return;
if(root.lchild == null && root.rchild == null){ //要删除的结点刚好的根结点
root = null;
return;
}
//2. 找到targetNode的父结点
BSTNode parent = searchParent(data, root);
//3. 如果要删除的是叶子结点
if(targetNode.lchild == null && targetNode.rchild == null){
//判断targetNode是父结点的左结点还是右结点
if(parent.lchild != null && parent.lchild.data == data)
parent.lchild = null;
else if(parent.rchild != null && parent.rchild.data == data)
parent.rchild = null;
//4. 删除有两课子树的结点
}else if(targetNode.lchild != null && targetNode.rchild != null){
int minVal = delRightTreeMin(targetNode.rchild);
targetNode.data = minVal;
//5. 删除只有一棵子树的结点
}else {
if(targetNode.lchild != null){ //如果要删除的结点有左子节点
if(parent != null){
if(parent.lchild.data == data)
parent.lchild = targetNode.lchild;
else
parent.rchild = targetNode.lchild;
}else
root = targetNode.lchild;
}else{ //如果要删除的结点有右子结点
if(parent != null){
if(parent.lchild.data == data)
parent.lchild = targetNode.rchild;
else
parent.rchild = targetNode.rchild;
}else
root = targetNode.rchild;
}
}
}
}
}
Test:
public class Test {
public static void main(String[] args) {
// int[] arr = {4,3,6,5,7,8}; //测试左旋转
// int[] arr = {10,12,8,9,7,6}; //测试右旋转
int[] arr = {7,6,10,11,8,9}; //测试右旋转
AVLTree avlTree = new AVLTree();
for (int i = 0; i < arr.length; i++) {
avlTree.insertAVL(new BSTNode(arr[i]));
}
avlTree.inOrderTraverse(avlTree.root);
System.out.println("平衡处理后:");
System.out.println("树的高度为:"+avlTree.getHeight(avlTree.root)); //树的高度为:3
System.out.println("树的左子树高度为:"+avlTree.getHeight(avlTree.root.lchild)); //树的左子树高度为:2
System.out.println("树的右子树高度为:"+avlTree.getHeight(avlTree.root.rchild)); //树的右子树高度为:2
}
}
6. B树
6.1 二叉树与B树
6.1.1 二叉树存在的问题
二叉树的操作效率较高,但是也存在问题, 请看下面的二叉树
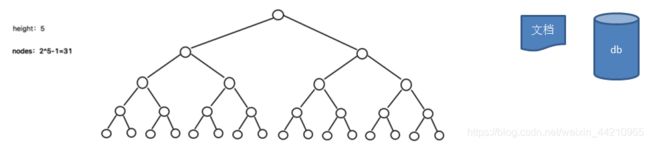
二叉树需要加载到内存的,如果二叉树的节点少,没有什么问题,但是如果二叉树的节点很多(比如1亿), 就存在如下问题:
- 问题1:在构建二叉树时,需要多次进行i/o操作(海量数据存在数据库或文件中),节点海量,构建二叉树时,速度有影响。
- 问题2:节点海量,也会造成二叉树的高度很大,会降低操作速度。
6.1.2 多叉树
1)在二叉树中,每个节点有数据项,最多有两个子节点。如果允许每个节点可以有更多的数据项和更多的子节点,就是多叉树(multiway tree)
2)后面我们讲解的2-3树,2-3-4树就是多叉树,多叉树通过重新组织节点,减少树的高度,能对二叉树进行优化。
6.1.3 B树的基本介绍
B树通过重新组织节点,降低树的高度,并且减少i/o读写次数来提升效率。

1)如图B树通过重新组织节点, 降低了树的高度.
2)文件系统及数据库系统的设计者利用了磁盘预读原理,将一个节点的大小设为等于一个页(页得大小通常为4k),这样每个节点只需要一次I/O就可以完全载入
3)将树的度M设置为1024,在600亿个元素中最多只需要4次I/O操作就可以读取到想要的元素, B树(B+)广泛应用于文件存储系统以及数据库系统中
6.2 2-3树
6.2.1 2-3树的基本介绍
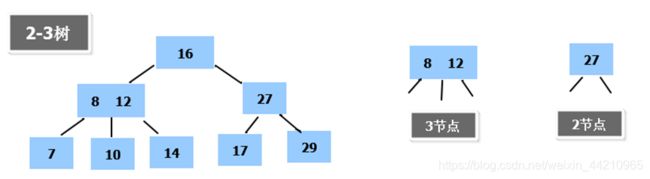
2-3树是最简单的B树结构, 具有如下特点:
- 2-3树的所有叶子节点都在同一层.(只要是B树都满足这个条件)
- 有两个子节点的节点叫二节点,二节点要么没有子节点,要么有两个子节点.
- 有三个子节点的节点叫三节点,三节点要么没有子节点,要么有三个子节点.
- 2-3树是由二节点和三节点构成的树。
6.2.2 2-3树应用案例
插入规则:
- 2-3树的所有叶子节点都在同一层.(只要是B树都满足这个条件)
- 有两个子节点的节点叫二节点,二节点要么没有子节点,要么有两个子节点.
- 有三个子节点的节点叫三节点,三节点要么没有子节点,要么有三个子节点
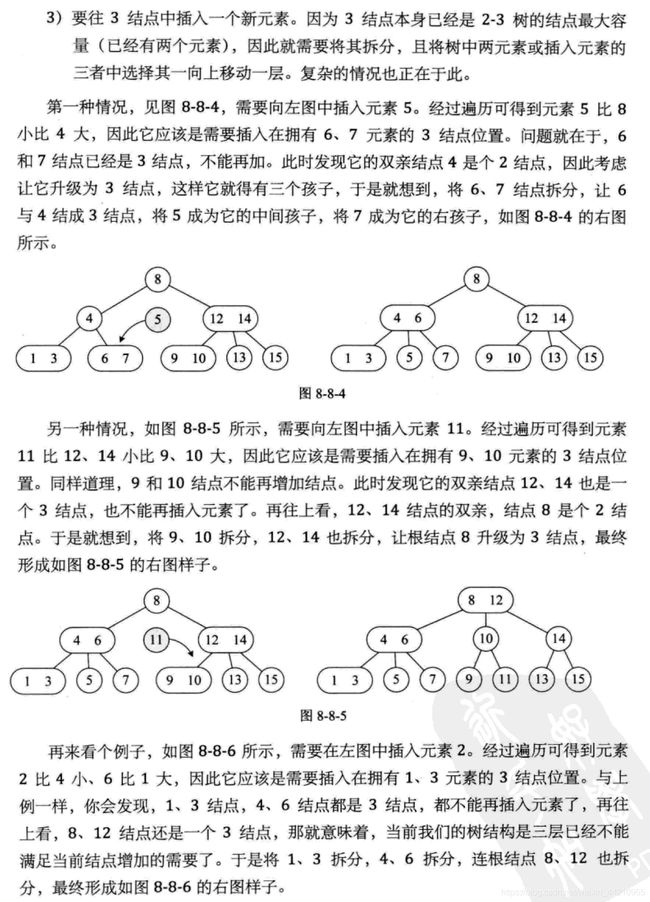
- 当按照规则插入一个数到某个节点时,不能满足上面三个要求,就需要拆,先向上拆,如果上层满,则拆本层,拆后仍然需要满足上面3个条件。
- 对于三节点的子树的值大小仍然遵守(BST 二叉排序树)的规则.
将数列{16, 24, 12, 32, 26. 14, 10, 8, 28, 34, 20, 38} 构建成2-3树,并保证数据插入的大小顺序。(演示一下构建2-3树的过程)



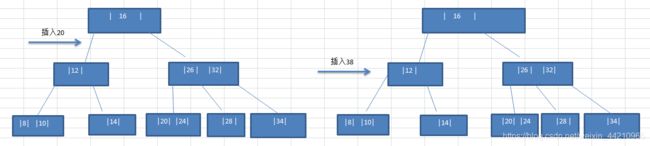
删除规则:
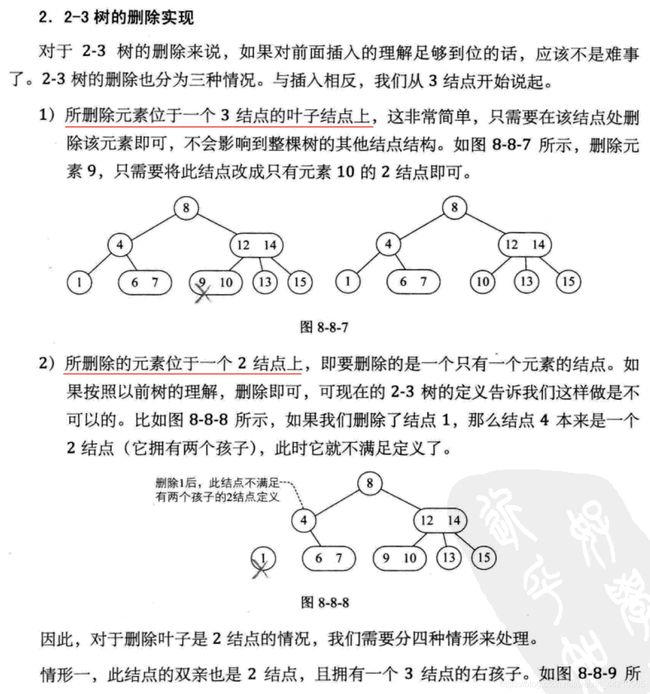
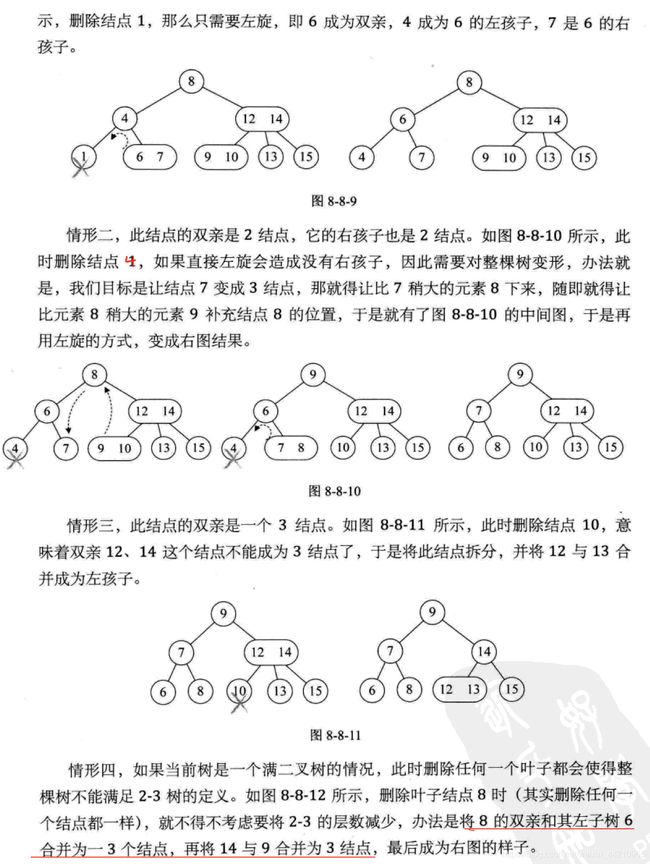

2-3树的详解可见《大话数据结构》的第八章第八节<多路查找树(B树)>
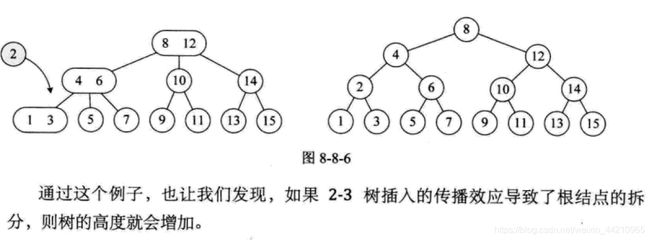
6.3 2-3-4树
6.4 B树、B+树和B*树
6.4.1 B树的介绍
B-tree 树即 B 树,B 即 Balanced,也有人把 B-tree 翻译成 B- 树。它是一种平衡的多路查找树,是一种特殊的多叉树,适合在磁盘等直接存取设备上组织动态的查找表。
2-3 树和 2-3-4 树,他们也是B树。我们在学习Mysql时,经常听到说某种类型的索引是基于B树或者B+树的,如图:
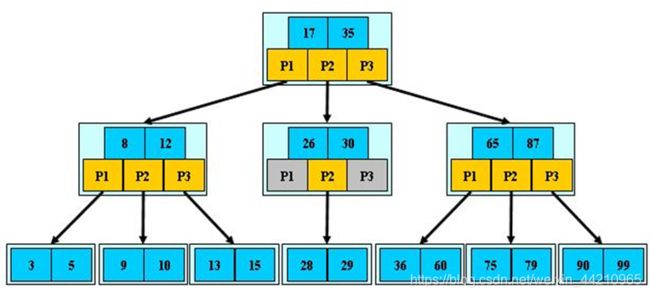
B树的说明:
- B 树的阶:节点的最多子节点个数。比如2-3树的阶是3,2-3-4树的阶是4。
- B 树的搜索,从根结点开始,对结点内的关键字(有序)序列进行二分查找,如果命中则结束,否则进入查询关键字所属范围的儿子结点;重复,直到所对应的儿子指针为空,或已经是叶子结点。
- 关键字集合分布在整颗树中, 即叶子节点和非叶子节点都存放数据。
- 搜索有可能在非叶子结点结束。
- 其搜索性能等价于在关键字全集内做一次二分查找。
6.4.2 B+ 树的介绍
B+ 树是 B 树的变体,也是一种多路搜索树。
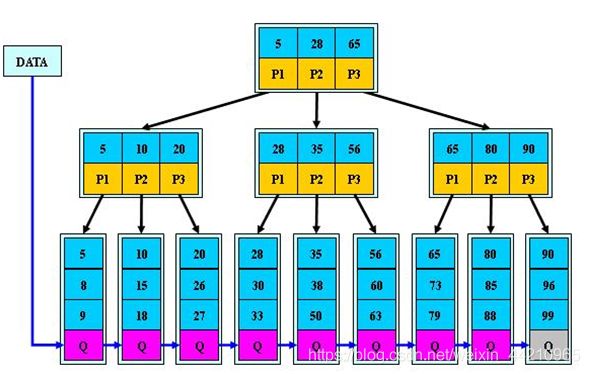
B+树的说明:
- B+ 树的搜索与 B 树也基本相同,区别是 B+ 树只有达到叶子结点才命中(B 树可以在非叶子结点命中),其性能也等价于在关键字全集做一次二分查找。
- 所有关键字都出现在叶子结点的链表中(即数据只能在叶子节点【也叫稠密索引】),且链表中的关键字(数据)恰好是有序的。
- 不可能在非叶子结点命中。
- 非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层
- 更适合文件索引系统。
- B 树和 B+ 树各有自己的应用场景,不能说 B+ 树完全比B树好,反之亦然。
6.4.3 B * 树的介绍
B * 树是 B+ 树的变体,在 B+ 树的非根和非叶子结点再增加指向兄弟的指针。
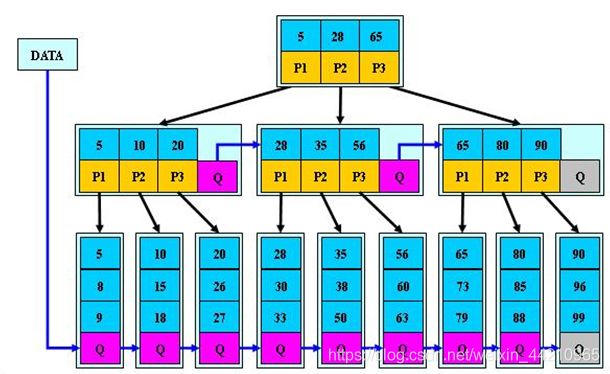
B*树的说明:
- B*树定义了非叶子结点关键字个数至少为(2/3)*M(M为该树的度),即块的最低使用率为2/3,而B+树的块的最低使用率为B+树的1/2。
- 从第1个特点我们可以看出,B*树分配新结点的概率比B+树要低,空间使用率更高。