C语言 递归函数
递归函数遵循1.函数直接或者间接调用自己,这样的函数我们把它称作递归的函数。
2.函数的退出条件。
3.形参上体现问题规模,而且问题规模一般为不断的缩小,直到达到函数退出条件。
递归的思想:
分解:大规模问题分解为小规模问题(问题规模缩小),直到小规模问题能够得到解决为止。
合并:将小规模的解逐层组合成原问题规模。
根据以上几点,我们抛出一个简单问题
使用递归求1+2+3+4?
#include
int Getsum(int n)
{
if(n == 1)
{
return 1;
}
return Getsum(n - 1) + n;
}
int main()
{
int res = Getsum(4);
printf("%d\n",res);
return 0;
} 过程如下:
右侧的箭头表示将n = 4带入,n不等于1,缩小规模直到达到退出条件。
左侧将值逐层返回至调用处。
接下来使用递归求斐波那契数列,求第n项的值。
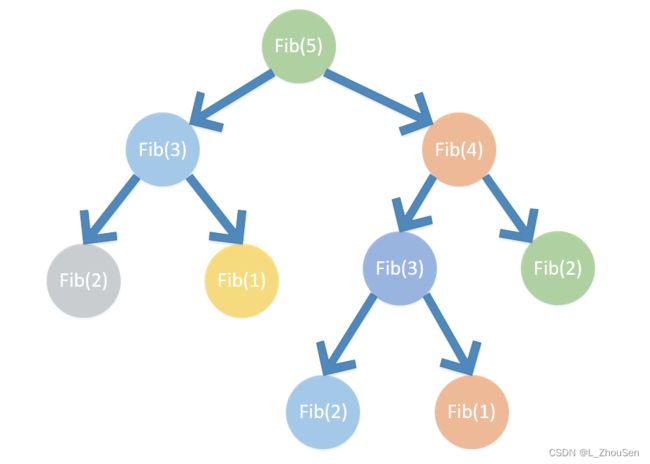
以n = 5来看我们分析递归的过程
当n = 6时,我们再分析一下:
我们会发现,n仅仅加了1,通俗的说就是这个图烦琐了很多,如果n = 30呢?
实际上,像斐波那契数列这种递归形式的定义容易诱导人们使用递归形式来解决问题,程序如下所示:
#include
int Fib(int n)
{
if(n == 1 || n == 2)
{
return 1;
}
return Fib(n - 1) + Fib(n - 2);
}
int main()
{
int res = Fib(5);
printf("%d\n",res);
return 0;
} 这里有一个陷阱:它使用递归步骤计算Fib(n-1)和Fib(n-2)。但是在Fib(n-1)时也将计算Fib(n-2)。这个额外的计算代价有多大呢?
答案是它的代价远远不止一个冗余计算——每个递归调用都触发另外两个递归调用,而这两个调用的任何一个还将触发两个递归调用,再接下去的调用也是如此。这样,冗余计算的数量增长的非常快。例如,在递归计算Fib(10)时,Fib(3)的值被计算了21次。但是,在递归计算Fib(30)时,Fib(3)的值被计算了317811次。当然,这317811次计算所产生的结果是完全一样的,除了其中之一外,其余纯属浪费。这个额外的开销真是相当的恐怖!
那么,对于该递归的缺陷,如果使用迭代呢?
迭代是使用一个简单的循环来代替递归。同样,这个循环形式不如递归符合前面斐波那契数列的抽象定义,但它的效率提高了几十万倍!
在使用递归方式实现一个函数之前,先问问自己使用递归带来的好处是否抵得上它的代价。而且必须小心:这个代价可能比初看上去要大得多!
用迭代方法解决斐波那契问题:
#include
long Fib(int n)
{
long res;
long previous_res;
long next_old_res;
res = previous_res = 1;
while(n > 2)
{
n -= 1;
next_old_res = previous_res;
previous_res = res;
res = previous_res + next_old_res;
}
return res;
}
int main()
{
int res = Fib(6);
printf("%d",res);
return 0;
} 再来一个使用递归解决二分查找问题
二分查找又称折半查找、二分搜索、折半搜索等,是在分治算法基础上设计出来的查找算法,对应的时间复杂度为O(logn)。
二分查找算法仅适用于有序序列,它只能用在升序序列或者降序序列中查找目标元素。
在有序序列中,使用二分查找算法搜索目标元素的核心思想是:不断地缩小搜索区域,降低查找目标元素的难度。
以在升序序列中查找目标元素为例,二分查找算法的实现思路是:
初始状态下,将整个序列作为搜索区域假设为 [A, E]);
找到搜索区域内的中间元素(假设所在位置为 M),和目标元素进行比对。如果相等,则搜索成功;如果中间元素大于目标元素,表明目标元素位于中间元素的左侧,将 [A, M-1] 作为新的搜素区域;反之,若中间元素小于目标元素,表明目标元素位于中间元素的右侧,将 [M+1, E] 作为新的搜素区域;
重复执行第二步,直至找到目标元素。如果搜索区域无法再缩小,且区域内不包含任何元素,表明整个序列中没有目标元素,查找失败
void Subblesort(int *arr, int len)
{
for(int i = 0; i < len-1; i++)
{
for(int j = 0; j < len-1-i; j++)
{
if(arr[j] > arr[j+1])
{
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
int BinarySearch(int *arr, int len, int left, int right , int value)
{
assert(arr != NULL && len > 0 && left > 0 && right > 0);
if(left > right || value < arr[left] || value > arr[right])
{
return -1;
}
int mid = (left+right) /2;
int midVal = arr[mid];
if(value > midVal)
{
return BinarySearch(arr,len,mid+1,right,value);
}
if(value < midVal)
{
return BinarySearch(arr,len,left,mid-1,value);
}
else
{
return mid;
}
}因为其仅使用于有序序列,以及我在本题中所遇到的问题(当数组内元素为0,1,2,3,4,5,6,7,10,8的顺序查找时,查找其中元素10,查找失败),我给其添加了一个冒泡排序,使其成为有序序列之后,再进行二分查找。
最后,我再说明一下函数的调用机制:
Step1:建立(开辟)栈帧空间
Stap2:保护现场:主调函数运行状态(记录并存入栈帧空间) 入栈
Step3:形参进行存储空间开辟,形参 拷贝 实参,然后对函数的局部变量进行内存分配
Step4:开始执行函数体
Step5:释放被调用函数的栈空间
Step6:恢复现场:此时被调用函数已经执行完毕,返回至主调函数的地址,继续主调函数的后续语句执行