TFHE：环面上全同态加密方案学习笔记3

LHE TFHE 中的 TBSR counter

笔记2中说到在 LHE TFHE 中可以使用 确定型加权有穷自动机 (det-WFA) 来实现 输出最大值 、单位数加法、多位数加法 (multi-addition) 或 多位数乘法 等运算。然而，有一种在计算 多位数加法 (或其派生) 时比一般的 加权自动机 更快的技术，叫作 TBSR (Bit Sequence Representation on TRLWE ciphertexts) 。

TBSR 的主要思想是建立一个表示小整数 ( 0 到 $N=2^p$ ) 的同态方案，只用于下面三种 多位数加法 中的 基础运算：

1. 提取 TRLWE sample 中的任意比特，作为 TLWE sample
2. 做 加 1 的操作
3. 做 除 2 的操作

接下来讲述这些操作如何在 TRLWE 密文上进行。

BSR 的概念

该方案中使用的小整数的计算机表示为：little endian signed binary representation (小字节序带符号的二进制表达)，小字节序即 低位字节排放在内存的低地址端，高位字节排放在内存的高地址端。小端字节序对于逻辑电路更有效率，大端字节序对用户友好。（详见计算机组成原理与系统结构类书籍）

对于 $j\in [0,p=lo{g}_2(N)]$ 和 $k,l\in \mathbb{Z}$ ，我们令 $B_{j,k}^{(l)}$ 为 $k+l$ 的 小字节序带符号的二进制表达 的第 $j$ 位。下面给一些简单的二进制序列：

• $B_0^{(0)}=(0,1,0,1,...)$ 是以 2 为周期的 (2 - periodic)
• $B_1^{(0)}=(0,0,1,1,0,0,1,1,...)$ 是以 4 为周期的 (4 - periodic)

更广义地说，对于 $j\in [0,p]$ 和 $l\in \mathbb{Z}$ ，$B_j^l$ 是 $2^j$ - antiperiodic 的，并且是 $B_j^{(0)}$ 左移 $l$ 位的结果。 因此，只要有 $2^j<N$ 位连续的值，就足够推出所有剩余的位 (blindly) 。注意对于每个整数 $k\in \mathbb{Z}$ ， $l+k$ mod $2N$ 的 (小字节序带符号的) 二进制表达 为： $B_{0,k}^{(l)},B_{1,k}^{(l)},...,B_{p,k}^{(l)}$ 。现取 $l=0,N=8,j\in [0,{\log }_{2}8=3]$ 为示范：

现在，我们定义 $BSR(l)=[B_0^{(l)},...,B_p^{(l)}]$ 为整数 $l\in [0,N-1]$ 的 比特序列表示 (Bit Sequence Representation) 。

下面介绍如何 在固定位 (与 $l$ 无关) 仅进行 复制 和 取反 操作 (blind computation)，计算 $BSR(l+1)$ 和 $BSR(\lfloor l/2\rfloor )$ 。随后再介绍如何在 TRLWE 密文中同态地进行这些操作。

BSR 上的 加法操作 和 除2操作

加法操作 (Increment)

令 $U=[u_0,...,u_p]$ 为某个未知数 $l\in [0,N-1]$ 的 BSR。我们的目标是计算 $l+1$ 的 BSR : $V=[v_0,...,v_p]$ 。由上面的周期特性我们发现，我们只需要定义 序列 $v_i$ 上 $N$ 个连续的值就足够了 (剩下的可以用周期性推出来) 。

想进行 +1 的操作，只需将序列移位 1 个位置 : $v_{j,k}:=u_{j,k+1}$ for all $k\in [0,N-1]$ 。事实上，这个操作只是将每一位 $B_{j,k}^{(l)}$ 变为了 $B_{j,k+1}^l=B_{j,k}^{(l+1)}$ ，输出就变为了 $l+1$ 的 BSR : $V$ 。例如，现在计算 $l+5$ ，其中 $l=0$ ：

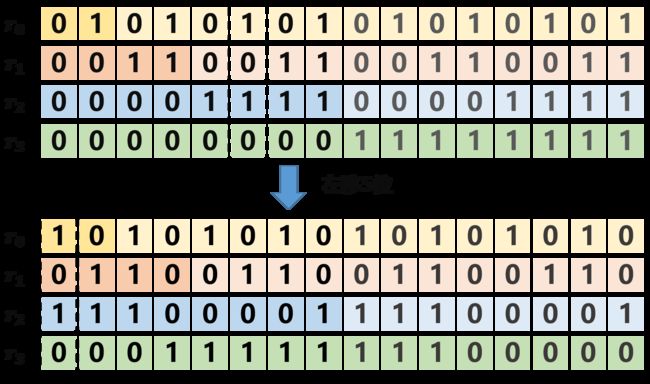
整数除 2 操作

令 $U=[u_0,...,u_p]$ 为某个未知数 $l\in [0,N-1]$ 的 BSR。我们的目标是计算 $\lfloor \frac{l}{2}\rfloor$ 的 BSR : $V=[v_0,...,v_p]$ 。首先，整数除 2 对应位的右移。因此，对于 $j\in [0,p-1]$ 和 $k\in \mathbb{N}$ ，我们可以设 $v_{j,k}=u_{j+1,2k}$ 。事实上， $u_{j+1,2k}$ 正是 $l+2k$ 的第 $j+1$ 位，也是 $\lfloor \frac{l}{2}\rfloor +k$ 的第 $j$ 位，正是我们想要的 $v_{j,k}=B_{j,k}^{\lfloor l/2\rfloor }$ 。不幸的是，这些不足以让我们直接重构最后的序列，因为我们不知道 $U$ 的 $p+1$ 位。

然而，在这个方案中，我们可以直接来重构最后的序列。首先，对于所有的 $k\in [0,N/2-1]$ ，都有 $\lfloor \frac{l}{2}\rfloor +k<N$ ，因此，只需设置对应的 $v_{p,k}=0$ 即可。随后，我们注意到 $(u_{p,0},...,u_{p,N-1})$ 必须包含 $N/2-l$ 个 0 接着 $\lfloor \frac{l}{2}\rfloor$ 个 1 。因此，我们所求的序列可以使用原序列的偶数位 $(u_{p,0},u_{p,2},...,u_{p,N-2})$ 填充。总结 除2转换 的对应位：

$$\{\begin{array}{rlrl}{v}_{j,k}& =& u_{j+1,2k}& forj\in [0,p-1],k\in [0,N-1]\\ v_{p,k}& =& 0& fork\in [0,\frac{N}{2}-1]\\ v_{p,N/2+k}& =& u_{p,2k}& fork\in [0,\frac{N}{2}-1]\end{array}$$

例如，现在计算 $\lfloor 5/2\rfloor =2$ ，先按照公式填入前三行：

再按照公式填入第四行并使用周期性补全剩余代码：

在TRLWE 密文下编码 BSR 序列

现在，我们将 BSR 序列 编码到 TRLWE 密文上：现在所有的系数从 $\mathbb{B}$ 变为了 环面上的元素，我们需要编码 N-periodic 或 N-antiperiodic 的序列。此外，因为 循环移位 在自增 (increment) 操作中被大量使用，我们把它关联到 乘以 $X$ (类似在环面多项式中对系数所做的操作) 。

Therefore, this is our basic encoding of the BSR sequences：令未知数 $l\in [0,N/2]$ 的 BSR 为： $U=[u_0,...,u_p]$ ，对于每个 $j\in [0,p-1]$ 我们用多项式 ${\mu }_i={\sum }_{k=0}^{N-1}\frac{1}{2}{u}_{j,k}{X}^k$ 代表 $u_j$ ，并且使用多项式 ${\mu }_p={\sum }_{k=0}^{N-1}(\frac{1}{2}{u}_{p,k}-\frac{1}{4})X^k$ 代表最后的 $u_p$ 。使用这种编码方式后，之前的整数除法变为一个仿射函数，将系数 $({\mu }_{j,k}{)}_{j\in [1,p],k\in [0,2,...,2N-2]}\in {\mathbb{T}}^{pN}$ 变为如下的 $({\mu }_0^{\prime },...,{\mu }_p^{\prime })$ ：

$${\pi }_{div2}:\{\begin{array}{rlrl}{\mu }_{j,k}^{\prime }& =& {\mu }_{j+1,2k}& forj\in [0,p-2],k\in [0,N-1]\\ {\mu }_{p-1,k}^{\prime }& =& {\mu }_{p,2k}+\frac{1}{4}& fork\in [0,N-1]\\ {\mu }_{p,k}^{\prime }& =& -\frac{1}{4}& fork\in [0,\frac{N}{2}-1]\\ {\mu }_{p,N/2+k}^{\prime }& =& {\mu }_{p,2k}& fork\in [0,\frac{N}{2}-1]\end{array}$$

最终，我们将未知数 $l\in [0,N-1]$ 的 TBSR 密文 设为 $C=[c_0,...,c_p]$ ：消息 $[{\mu }_0,...,{\mu }_p]$ 的 TRLWE 密文。

TBSR 实现 多位加法 与 乘法 的算法可以参考论文：Faster packed homomorphic operations and efficient circuit bootstrapping for TFHE 中附录的 算法8 与 算法9。

TFHE 中的自举

以下部分内容摘自 笔记1
2009年Gentry提出了自举的最naïve的设想。整个自举过程如下：

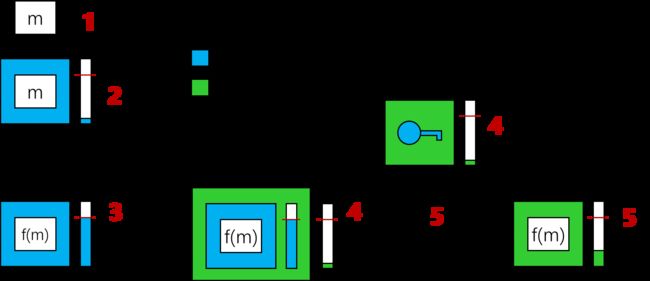
1. 现有一明文m。
2. 使用$p{k}_1$对该明文进行加密，得到一个密文，此时密文新鲜(fresh)，噪声较小。假设如果噪声不超过框中的红线，就可以正确地进行解密。
3. 经过一系列的评估操作之后，噪声不断增大，现在噪声已经达到红线，必须将噪声减小才能继续进行计算。最直观地方法就是对其进行解密，因为解密之后噪声会消失，但是解密需要密钥，如果这个过程在云服务器上执行的话客户端是不可能给出自己的私钥的。
4. 于是Gentry想了一个办法，他将解密函数Dec作为评估函数中的f，再用一个新的公钥$p{k}_2$将整个密文加密，用户的私钥$s{k}_1$(对应公钥$p{k}_1$)也使用$p{k}_2$进行加密后给云服务器。
5. 这时候云服务器就可以在$p{k}_2$加密下进行同态解密，从而得到$p{k}_2$加密的f(m)，此时噪声比之前少了许多，能够支持至少一次的乘法运算。

通过这样的自举步骤，同态加密的运算便能够不断地持续地进行。

因此，为实现任意深度电路的同态评估，需要为TFHE引入自举(bootstrapping)操作。

自Gentry于2009年提出自举以来，自举从同态解密(Gentry09)，到重加密，到压缩解密函数，再到密钥交换&模交换(FHEW&TFHE使用)。在Gentry09的自举是一个单独的函数，仅用于减小噪声；而在TFHE中，自举可以改变消息内容。TFHE中自举方案分为两种：门自举 (gate bootstrapping) 与 电路自举 (circuit bootstrapping) 。

两种自举在 TFHE 的三种形式的密文中有如下转换：

门自举的输入为噪声大的 TLWE 密文，输出为噪声小的 TLWE 密文。电路自举输入为噪声大的 TLWE 密文，输出为噪声小的 TRGSW 密文。接下来介绍TFHE中的自举门(gate bootstrapping)。

TFHE 中的门自举

TFHE 的门自举常常用在 FHE 模式中，与布尔电路结合，在每通过一个门电路 前/后 便自举一次，类似如下情况：

我们现在有一个二进制的消息空间，消息只有 false( $-\frac{1}{8}=\frac{7}{8}$ ) 和 true ( $\frac{1}{8}$ ) ，噪声均小于 $\frac{1}{16}$ 。我们把两个消息 ( 环面上 ) 相加，有三种情况：

1. 两个都是假，得到 $\frac{3}{4}$ $(红色)$ 。
2. 一真一假，得到 $0$ $(黄色)$ 。
3. 两个都是真，得到 $\frac{1}{4}$ $(绿色)$ 。

在这种明文的条件下，怎么进行自举呢？很简单，在这个环面上画一条线，落在线左边输出 $true$ ，落在线右边输出 $false$ 。难点在于我们如何在密文下进行操作。TFHE给出了这样的答案：

1. 首先从一个(平凡的)TLWE$(v_0+v_{1}X+\dots +v_{(}N-1)X^{(}N-1){)}^a$开始
2. 将其旋转$p=-{\phi }_s(a,b)$个位置
3. 取出常数项constant term(其加密$v_p$)

最困难的部分在第2步。将环面旋转$p$个位置有两种情况：
在$p$已知的情况下，旋转操作为$(X^p\cdot c)$。
在$p$未知的情况下，旋转操作为$(TGSW(X^p)⊡c)$。
那么，如何在未知s(私钥)的情况下，旋转$-{\phi }_s(a,b)=-b+{\sum }_{i=1}^n{a}_i{s}_i$个位置呢？

1. 首先反方向旋转$b$个位置，即Multiply by $X^{-b}$，$b$为密文，事先知道可以直接计算。
2. For $i\in [1,n]$ multiply by $TGSW(X^{-a_i{s}_i})$
   $X^{a_i{s}_i}=1+(X^{a_i}-1)\cdot s_i,s_i\in \{0,1\}$
   $TGSW(X^{a_i{s}_i})=h+(X^{a_i}-1)\cdot TGSW(s_i),BK=TGSW(s_i)$
   私钥$s$事先未知，将其变为公钥$BK$(Bootstrapping Key)。

完成这两部就能够完成这个旋转的任务。

以下为更加形象化、更加用户友好的理解：
可以将整个自举过程视为如下的操作：

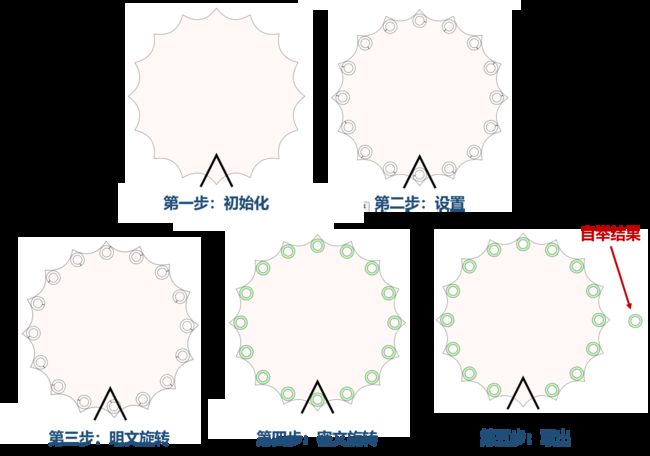
1. 首先将环面分为 $2N$ 个部分，想象成图中的轮子，上面带有 $2N$ 个槽。
2. 然后将要返回的 $2N$ 个值放入槽中，完成设置 (Setup) 步骤。
3. 进行明文旋转 (PlainRotate) 过程，该过程进行旋转的人可以知道具体旋转了多少个位置。
4. 进行密文旋转 (EncRotate) 过程，该过程进行旋转的人不知道旋转了多少个位置，并且得到的是加密的密文，无法通过旋转前后判断旋转了多少位置。可以理解为放在一个黑盒中进行了一波操作。
5. 最终将 0 位置的密文取出，即为所需要的结果。

自举中密文旋转的密文类型：

TFHE 中的电路自举

TFHE 的电路自举常常用在 LHE 模式中，与 LHE 算法 (如 det-WFA, TBSR) 结合，在每通过较大的电路后再自举一次，类似如下情况：

注意到之前介绍的高效 LHE 算法 (例如 det-WFA, TBSR) 的输入和输出是不同的密文类型 (例如 输入为 TRGSW 密文，输出为 TLWE 密文) ，因此不能进行组合操作。而电路自举可以做到这件神奇的事情。电路自举的目标为：将二进制消息空间的噪声较大的 TLWE sample 变为 整型消息空间的噪声较小的 TRGSW sample 。

LHE TFHE 方案中加密的 level 可以归为如下三层：

图中的箭头表示可以进行的操作以及如何在不同的 level 之间转换；图中字幕的上划线表示 level 2 中的变量，下划线表示 level 0 中的变量，其余表示 level 1 中的变量。图中蓝色部分为电路自举的步骤。

• Level 2 中噪声最小 (一般 $\underline{\alpha }\ge 2^{-50}$) 。
• Level 1 中噪声中等 (一般 $\underline{\alpha }\ge 2^{-30}$) ，参数大小中等，允许相对快速的操作 (例如对一个相对大的自动机进行 LHE 评估) 。
• Level 0 中噪声最大 (一般 $\underline{\alpha }\ge 2^{-11}$) ，参数很小，计算几乎是瞬时完成，但是只允许非常有限的线性操作。

电路自举的步骤：

1. -TLWE-to-TLWE Pre-keyswitch : 输入为 消息空间 $\{0,\frac{1}{2}\}$ 的TLWE sample 。输出为 消息空间 $\mu \in \mathbb{B}$ 的 Level 0 的 TLWE 密文。
2. -TLWE-to-TLWE Bootstrapping : 输入为 Level 2 的自举密钥。将该算法执行 $l$ 次得到 $l$ 个 TLWE 密文。
3. -TLWE-to-TLWE private key-switching : 使用 gadget 矩阵 重构 $\mu$ 的 TRGSW 密文。

Circuit Bootstrappping 算法简略总结：

• 输入：一个 Level 0 的 TLWE sample $\underline{\mathfrak{c}}=(\underline{\mathfrak{a}},\underline{\mathfrak{b}})\in TLW{E}_{\underline{\mathfrak{K}},\underline{\eta }}(\mu \cdot \frac{1}{2})$ ，其中 $\mu \in \mathbb{B}$
• 输入：一个自举密钥 $B{K}_{\underline{\mathfrak{K}}\to \overline{\mathfrak{K}},\overline{\alpha }}$
• 输入： $k+1$ 个 private 密钥转换密钥 $K{S}_{\underline{\mathfrak{K}}\to K,\gamma }^{(f_u)}$
• 输出：一个 Level 1 的 TRGSW sample $C\in TRGS{W}_{K,\eta }(\mu )$

TFHE 中方案总结

目前所学 TFHE 中主要方案以及对应算法库链接如下：

压缩技术可用于 LUT 评估以及 Level 模式中。

主要参考论文：

• Chillotti I, Gama N, Georgieva M, et al. Faster fully homomorphic encryption: Bootstrapping in less than 0.1 seconds[C]//international conference on the theory and application of cryptology and information security. Springer, Berlin, Heidelberg, 2016: 3-33.
• Chillotti I, Gama N, Georgieva M, et al. Faster packed homomorphic operations and efficient circuit bootstrapping for TFHE[C]//International Conference on the Theory and Application of Cryptology and Information Security. Springer, Cham, 2017: 377-408.

算法库：

• https://tfhe.github.io/tfhe/
• https://github.com/tfhe/experimental-tfhe

本文仅供个人学习使用