管理类联考——数学——汇总篇——知识点突破——代数——不等式——记忆

本篇思路：根据各方的资料，比如名师的资料，按大纲或者其他方式，收集/汇总考点，即需记忆点，在通过整体的记忆法，比如整体信息很多，通常使用记忆宫殿法，绘图记忆法进行记忆，针对局部/细节/组成的部分，可通过多种方法，比如联想记忆法、理解记忆法等进行进一步记忆。

考点

通过汇总各方大佬资料，作为收集考点/记忆点的信息输入：XX，收集汇总如下：

汇总考点的必要，或者说，汇总记忆的内容的必要，不言而喻，首先，你要记忆东西，得有东西，所以你要梳理出你需要记忆的全部东西，其次，在收集多个大佬的梳理的考点，又可以找出各条逻辑帮助记忆考点，所以，梳理考点是很有必要的，是记忆的基础，是记忆宫殿里面的物品，是我们最后考试需要去找到的解题物品。

记忆/考点汇总——按大纲

——不等式——

糖水不等式：
若$a＞b＞0，m＞0$，则$\frac{b}{a}＜\frac{b+m}{a+m}$——【歌诀记忆法：往糖水里加糖，越加越甜】
解不等式步骤：①去分母；②去括号；③移项；④合并同类项；⑤化系数为1。(步骤①和⑤中，乘数或除数是负数时，要改变不等号的方向)。
解不等式组步骤：①分别求出不等式组中各个不等式的解集；②利用数轴画出这些不等式的解集，其公共部分为不等式组的解集。

一元二次不等式——【类比记忆法：一元二次不等式其实是一元二次函数的函数值大于/小于0时的情况】
标准形式：$a{x}^2+bx+c＞0(或＜0)$，其他非标准形式的不等式可以通过等价变形转化为标准形式，即将原不等式化为$a{x}^2+bx+c＞0/＜0且a＞0形式$。——【若不等式中a＜0，必须将其化为正值进行求解】
解集：——【图形记忆法：画出一元二次函数图形辅助判断】
$△＞0$时，$a{x}^2+bx+c＞0(a＞0)$的解集为{$x|x＜x_1或x＞x_2$}；——【二次项系数为正，不等式小于0，解集取两边：大于大的或小于小的】
$△＞0$时，$a{x}^2+bx+c＜0(a＞0)$的解集为{$x|x_1＜x＜x_2$}；——【二次项系数为正，不等式大于0，解集取中间：大于小的，小于大的】
$△=0$时，$a{x}^2+bx+c＞0(a＞0)$的解集为{$x|x\ne x_1\ne -\frac{b}{2a}$}；——【转换为一元二次图像抛物线（不等式函数化），需y＞0，即不要与x轴相交那点即可】
$△=0$时，$a{x}^2+bx+c＜0(a＞0)$的解集为$无解$；——【转换为一元二次图像抛物线，开头向上，交x轴一点，y恒大于等于0】
$△＜0$时，$a{x}^2+bx+c＞0(a＞0)$的解集为$x\in R$；
$△＜0$时，$a{x}^2+bx+c＜0(a＞0)$的解集为$无解$。
PS：若不等式带等号，只需在解集中增加两个根即可（即根的取值范围取闭区间）

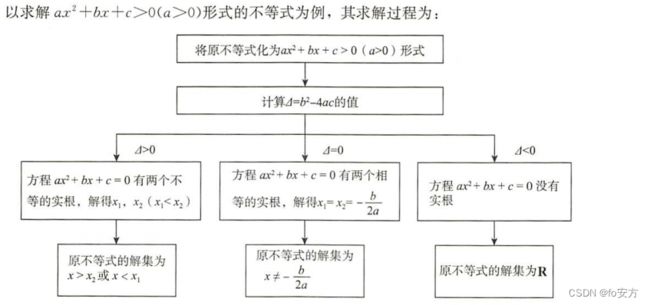
求解步骤：
（1）先化成标准型：$a{x}^2+bx+c>0(或<0)，且a>0$；——【一边为零，二次项系数大于0（是两个要求），其他跟一元二次方程一样，先确认根的多少，后进行求根】——【字头歌诀法：化正零，确根数，再求根，大鱼吃中间，小鱼吃两边】
① 将不等式的一边必须变为0（不等式的函数化）——【移项使得一边为0】
② 将其二次项系数必须变成正，即$a＞0$——【建议把所有的二次项系数为负转化为正再进行求解】
（2）计算对应方程的判别式$△$；——【避免做出不必要的错误判断，验证判别式是否大于等于零，若不是，考虑恒成立】
（3）求对应方程的根：十字相乘法（首选），求根公式；
（4）写解集：大于零在两边，小于零在中间。——【
将原不等式化为$a{x}^2+bx+c＞0/＜0且a＞0形式$
$⟹$ $判别式△=b^2-4ac$
$⟹$ $△$＞0，方程有两根，即求根公式$x_{1,2}$=$\frac{-b\pm \sqrt{△}}{2a}$；图像抛物线与x轴有两个交点；不等式解集为{$x|x＜x_1或x＞x_2$}/{$x|x_1＜x＜x_2$}。
$⟹$ $△$＝0，方程有一根，$x$为$-\frac{b}{2a}$；图像抛物线与x轴有一个交点；不等式解集为{$x|x\ne -\frac{b}{2a}$}/无解。
$⟹$ $△$＜0，方程无根；图像抛物线与x轴没有交点；不等式解集为$x\in R$/无解。】
＞＜0恒成立：$a{x}^2+bx+c＞（＜0）$恒成立时，
第一步：考虑特殊情况，要注意$a,b$中是否有同样的因式，若有则可以令$a=b=0$，$c＞（＜）0$即可；
第二步：考虑一般情况，——【$△$＜0$⟹$ 方程无根；图像抛物线与x轴没有交点；不等式解集为$x\in R$/无解；不等式恒成立】
一元二次不等式恒大于0的条件为$$\{\begin{array}{l}a＞0\\ △＜0\end{array}$$
一元二次不等式恒小于0的条件为$$\{\begin{array}{l}a＜0\\ △＜0\end{array}$$
特殊地，无解问题先转化成恒成立问题，如$a{x}^2+bx+c＞0(a\ne 0)$无解$⟹$ $a{x}^2+bx+c\le 0(a\ne 0)$恒成立。

区间内恒成立：——【区间内恒成立，用：分离参数法】
模型识别：
（1）一元二次不等式$a{x}^2+bx+c>0$或$a{x}^2＋bx+c<0(a\ne 0)$，在x属于某一区间时恒成立，求某个参数的取值范围。
（2）一元二次不等式$a{x}^2＋bx＋c>0$或$a{x}^2＋bx＋c<0(a\ne 0)$，在某个参数属于某区间时恒成立，求x的取值范围。
解题方法：
分离参数法，若题干中求α的取值范围，就把α分离出来，得到α与其余字母的数量关系，例如$a\le g(b)$，应用求最值的方法，求出$g(b)$的最值，由此可推出α的取值范围。

均值不等式
算术平均值：设有n个数$x_1,x_2,...,x_n$，称$x=\frac{x_1+x_2+...+x_n}{n}$为这n个数的算术平均值
几何平均值：设有n个正数$x_1,x_2,...,x_n$，称$\sqrt[n]{x_1{x}_2...x_n}$为这n个正数的几何平均值
基本定理：当$x_1,x_2,...,x_n$为n个正数时，它们的算术平均值不小于它们的几何平均值，$\frac{x_1+x_2+...+x_n}{n}\ge \sqrt[n]{x_1{x}_2...x_n}$$(x_i＞0，i=1,...,n)$，当且仅当$x_1=x_2=...=x_n$时，等号成立。
说明：平均值定理的本质是研究“和”与“积”的大小关系，即$\frac{和}{n}\ge \sqrt[n]{积}$
最值应用——【歌诀记忆法：积定和最小，和定积最大】
平均值定理求最值：先验证给定函数是否满足最值三条件：①各项均为正；②乘积（或者和）为定值；③等号能否取到；然后利用平均值公式求出最值。可总结为口诀“一正二定三相等”。
【注意】利用均值不等式求最值时要注意“一正二定三相等”：
①一正（使用均值不等式的前提）：$x_1,x_2,...,x_n$为正实数；——【各项均为正】
②二定（使用均值不等式的目标）：和为定值或积为定值时才有最值；——【当乘积为定值时，和有最小值：$和\ge n\sqrt[n]{积}$，当和为定值时，乘积有最大值：$积\le (\frac{和}{n}{)}^n$】
③三相等（取到最值时的条件）：当且仅当$x_1=x_2=...=x_n$时，等号成立。
模型识别：（1）已知几个字母的和或积的值，求另外一个代数式的最值。（2）类似对勾函数的问题。

构造定值：（1）拆项法：拆项常拆次数较小的项，并将其拆成相等的几项；（2）统一换元法：对已知条件进行变形，出现多个公共部分，并对其换元。

常用公式：
正实数成立：若$a,b\in R_{+}$，则$\frac{a+b}{2}\ge \sqrt{ab}$，可得$a+b\ge 2\sqrt{ab}$，$ab\le (\frac{a+b}{2}{)}^2$（当且仅当$a=b$时取“=”）
正实数成立：若$a,b,c\in R_{+}$，则$\frac{a+b+c}{3}\ge \sqrt[3]{abc}$，$abc\le (\frac{a+b+c}{3}{)}^3$（当且仅当$a=b=c$时等号成立）；
任意实数成立：若$a,b\in R$，则$\frac{a^2+b^2}{2}\ge ab$，可得$a^2+b^2\ge 2ab$（当且仅当$a=b$时取“=”）
若$x＞0$，则$x+\frac{1}{x}\ge 2$（当且仅当$x=\frac{1}{x}$时等号成立）。
——【 完全平方：$a^2\pm 2ab+b^2=(a\pm b{)}^2\ge 0$ $⟹$ 均值不等式
$⟹$ $\frac{a^2+b^2}{2}\ge ab$，可得$a^2+b^2\ge 2ab$
$⟹$ $\frac{a+b}{2}\ge \sqrt{ab}$，可得$a+b\ge 2\sqrt{ab}$
$⟹$ $\frac{a+b+c}{3}\ge \sqrt[3]{abc}$，$abc\le (\frac{a+b+c}{3}{)}^3$
$⟹$ $x+\frac{1}{x}\ge 2$
】

倒数情况：——【歌诀记忆法：b变号，根变号；ac互换，根为倒】
（1）若$x＞0$，则$x+\frac{1}{x}\ge 2$（当且仅当$x=1$时取“=”）；若$x＜0$，则$x+\frac{1}{x}\le -2$（当且仅当$x=-1$时取“=”）
（2）若$x\ne 0$，则$|x+\frac{1}{x}|\ge 2$即$x+\frac{1}{x}\ge 2$或$x+\frac{1}{x}\le -2$（当且仅当a=b时取“=”）
（3）若$ab＞0$，则$\frac{a}{b}+\frac{b}{a}\ge 2$（当且仅当a=b时取“=”）；若$ab\ne 0$，则$|\frac{a}{b}+\frac{b}{a}|\ge 2$即$\frac{a}{b}+\frac{b}{a}\ge 2$或$\frac{a}{b}+\frac{b}{a}\le -2$（当且仅当a=b时取“=”）
和与平方：
若$a,b\in R$，则$(\frac{a+b}{2}{)}^2\le \frac{a^2+b^2}{2}$（当且仅当a=b时取“=”）

特殊情况：
当n=2时，$a+b\ge 2\sqrt{ab}(a,b＞0)$；尤其$a+\frac{1}{a}\ge 2（a＞0）$即对于正数而言，互为倒数的两个数之和不小于2，且当a=1时取得最小值2。

重要不等式链：若a＞0，b＞0，则
$$\frac{2}{\frac{1}{a}+\frac{1}{b}}=\frac{2ab}{a+b}\le \sqrt{ab}\le \frac{a+b}{2}\le \sqrt{\frac{a^2+b^2}{2}}$$
当且仅当a=b时等号成立，此不等式链可以扩展到n个数。
【调和平均数≤几何平均数≤算术平均数≤平方平均数】

秒杀方法：
（1）直接取等法
均值不等式的解题口诀为“一正二定三相等”。“三相等”的意思是均值不等式等号成立的条件为不等式中的几个对象相等，故有些题可直接取等，得出结果。
（2）特殊值法
遇到题干中全是字母的不等式问题。无论是不是考查均值不等式，往往都可以使用特殊值法求解。

对勾化：
对勾化考法有以下两种形式：
(1)已知$ax+by=c$，求$\frac{m}{x}+\frac{n}{y}$的最小值（a，b，m，n均为正数）；
(2)已知$\frac{a}{x}+\frac{b}{y}=c$，求$mx＋ny$的最小值；
这两种考法的最小值都为$min=\frac{1}{c}(\sqrt{ma}+\sqrt{nb}{)}^2$。
【注意】根号里面分别为：与x相关的系数相乘，与y相关的系数相乘。

绝对值不等式
解绝对值不等式的基本思想是去掉绝对值符号，把含有绝对值号的不等式等价转化为不含绝对值号的不等式求解，常用的方法有：
（1）分段讨论法：——【零点问题的分类讨论】$$|f(x)|=\{\begin{array}{ll}f(x),& \text{f(x)≥0}\\ -f(x),& \text{f(x)＜0}\end{array}$$
（2）平方法：$|f(x){|}^2=[f(x){]}^2$——【两边均为非负才能进行平方法】
平方法扩展：
形如$|f(x)|,\sqrt{f(x)}>a$，在确保a为非负的时候可以直接平方，一定注意根号里面的定义域；
形如$|f(x)|,\sqrt{f(x)}＜a$，在确保a为非负的时候可以直接平方，以免漏掉定义域；
形如两个绝对值或者两个根号的情况，形如：$|x|<|y|$，果断平方（一定和三角不等式区分开来）——【总结：平方法的运用需要确保两边均为非负的属性，只要具备这个属性，不管是解方程还是解不等式，平方法横扫千军。】
（3）公式/转化法：——【绝对值的几何意义】
当$a＞0$时，
$|f(x)|＞a(a＞0)$ $⟺$ $f(x)＜-a或f(x)＞a$。
$|f(x)|＜a(a＞0)$ $⟺$ $-a＜f(x)＜a$。
当$a＜0$时，
$|f(x)|＞a(a＜0)$ $⟺$ $f(x)\in R$。——【a为负数，绝对值肯定大于它】
$|f(x)|＜a(a＜0)$ $⟺$ $f(x)空集$。
公式法扩展：
$|f(x)|＜g(x)$ $⟺$ $-g(x)＜f(x)＜g(x)$，($g(x)$为正)。
$|f(x)|＞g(x)$ $⟺$ $f(x)＞g(x)或f(x)＜-g(x)$，($g(x)$为正)。
$|f(x)|＞|g(x)|$ $⟺$ $f^2(x)＞g^2(x)$。
（4）图像法：若画图容易，可画出图像分析。
总结：当绝对值比较简单时，可以采用分段讨论求解。当绝对值内部次方较高时，采用公式法求解。当两边都有绝对值时，可以采用平方法求解。

指数不等式
（1）同底去底法：
$a＞1时，a^{f(x)}＜a^{g(x)}$ $⟺$ $f(x)＜g(x)$；
$0＜a＜1时，a^{f(x)}＜a^{g(x)}$ $⟺$ $f(x)＞g(x)$；
（2）化成对数式：
$a＞1时，a^{f(x)}＜b$ $⟺$ $a^{f(x)}＜a^{lo{g}_{a}b}$ $⟺$ $f(x)＜lo{g}_{a}b$；——【$a^{lo{g}_{a}b}=b$】
$0＜a＜1时，a^{f(x)}＜b$ $⟺$ $a^{f(x)}＜a^{lo{g}_{a}b}$ $⟺$ $f(x)＞lo{g}_{a}b$；
（3）取同底对数：
$a^{f(x)}＜b^{g(x)}$ $⟺$ $lg{a}^{f(x)}＜lg{b}^{g(x)}$ $⟺$ $f(x)lga＜g(x)lgb$。
对数不等式
（1）同底去底法：
$a＞1时，lo{g}_{a}f(x)＜lo{g}_{a}g(x)$ $⟺$ $0＜f(x)＜g(x)$；
$0＜a＜1时，lo{g}_{a}f(x)＜lo{g}_{a}g(x)$ $⟺$ $f(x)＞g(x)＞0$；
（2）化成指数式：
$a＞1时，lo{g}_{a}f(x)＜b$ $⟺$ $lo{g}_{a}f(x)＜lo{g}_a{a}^b$ $⟺$ $0＜f(x)＜a^b$；
$0＜a＜1时，lo{g}_{a}f(x)＜b$ $⟺$ $lo{g}_{a}f(x)＜lo{g}_a{a}^b$ $⟺$ $f(x)＞a^b＞0$。

分式不等式
（1）简单分式不等式
①$\frac{x-a}{x-b}\ge 0(a<b)$的解集为{$x|x\le a或x>b$}。
②$\frac{x-a}{x-b}\le 0(a<b)$的解集为{$x|a\le x<b$}。
（2）其他分式不等式
分式不等式的解法一般通过移项整理成标准型$\frac{f(x)}{g(x)}>0或\frac{f(x)}{g(x)}<0$，再等价化成整式不等式来解。
①$\frac{f(x)}{g(x)}>0⟺f(x)\cdot g(x)>0$
②$\frac{f(x)}{g(x)}<0⟺f(x)\cdot g(x)<0$
③$\frac{f(x)}{g(x)}\ge 0⟺f(x)g(x)\ge 0且g(x)\ne 0$
④$\frac{f(x)}{g(x)}\le 0⟺f(x)g(x)\le 0且g(x)\ne 0$
最后再讨论各因子的符号或按数轴标根法写出解集。
（3）当$0＜a\le b$，且$m\ge 0$时，有$\frac{a+m}{b+m}\ge \frac{a}{b}$，其中，当且仅当$a=b$或$m=0$时等号成立。

解题步骤：
第一步：移项：将$\frac{f(x)}{g(x)}>a$化为$\frac{f(x)}{g(x)}-a＞0$；——【在对不等式两边乘除时，切不可直接通过乘以分母来去掉分母（如果分母出现二次函数，其正负性无法确定）】——【归类记忆法：一元二次不等式和分式不等式解题步骤的第一步都是移项使得一边为0。】
第二步：通分：将$\frac{f(x)}{g(x)}-a＞0$化为$\frac{f(x)-a\cdot g(x)}{g(x)}＞0$；
第三步：分母乘以分子，化为整式不等式求解集。——【通过移项、通分、合并，用分母乘以分子，化为整式不等式求解集】
第四步：求出定义域，求解集与定义域的交集。
备注：分式不等式一般涉及高次不等式的求解，高次不等式的求解的通解通法为数轴标根法（穿针引线法）

高次不等式——穿线法
“数轴标根法/数轴穿线法/穿针引线法”用于解一元高次不等式非常方便，其解题步骤如下：

穿线法步骤：——【穿线法是用来解分式不等式和高次不等式的方法】
第一步：移项，使等式右侧为0；
第二步：分解因式，化成若干个因式的乘积的形式，分解到不可分解为止；
第三步：作等价变形，便于判断因式的符号，例如：$x^2+1,x^2+x+1,x^2-3x+5$等，这些因式的共同点是：无论x取何值，它们的值恒大于0；
第四步：将分解所得到的每一个因式的最高次项的系数化为正数；
第五步：令每个因式等于零，得到零点；
第六步：由小到大，从左到右标出与不等式对应的方程的根/零点；
第七步：如果有恒大于0的项，对不等式没有影响，直接删掉；
第八步：穿线：从数轴的右上方开始穿线，依次去穿每个点，遇到奇次幂零点则穿过，遇到偶次幂零点则碰而不过；——【歌诀记忆法：穿线法原则：从右上角开始，穿针引线，奇穿偶不穿/奇过偶不过（联想拳头被铁线穿过露出来的骨头）】
第九步：根据图像写出解集，注意能否取到等号：凡是位于数轴上方的曲线所代表的区间，就是令不等式大于0的区间；数轴下方的，则是令不等式小于0的区间；数轴上的点，是令不等式等于0的区间，但是要注意这些零点是否能够取到。
画出解集的示意区域，如图4-1，从左到右写出解集。
$f(x)=(x-x_1)(x-x_2)...(x-x_n)$

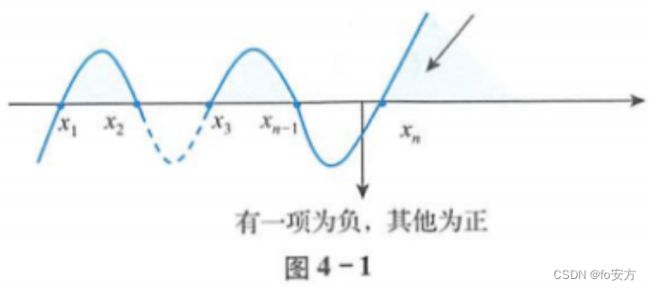
遇零点变号，阴影部分为$f(x)>0$的解集。
评注：穿线法是先在数轴上标注出每个因式的零点，然后从右上方穿一条线，遇到零点就穿过一次，图像在数轴上方代表大于零，在数轴下方代表小于零。需要注意的是，对于偶数次方的因式，该零点不穿透。另外在使用穿线法的时候，x的系数都要转化为正数来分析。
遇到高次方可分解因式的不等式问题，一般方法是等价变形，采用简洁的穿线方法求解。

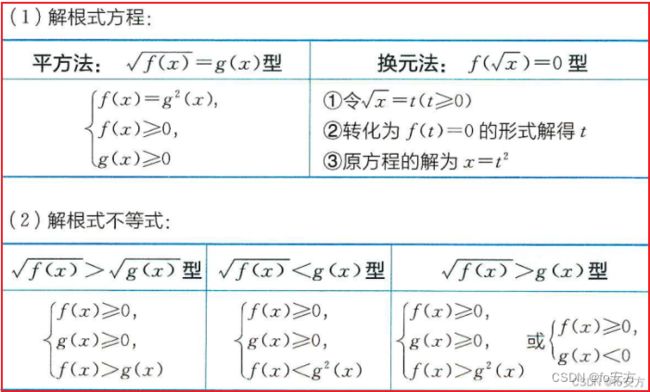
根式不等式——【与根式方程一起记忆最佳】
对于无理不等式，一般是通过平方转化为有理不等式进行求解。在求解时，注意根号要有意义。
遇到物理不等式，先去掉根号，在遇到偶次方根时不要忘记定义域。
$$（1）\sqrt{f(x)}\ge g(x)⟺\{\begin{array}{l}f(x)\ge 0\\ g(x)\ge 0\\ f(x)\ge g^2(x)\end{array}$$
or
$$\sqrt{f(x)}\ge g(x)⟺\{\begin{array}{l}f(x)\ge 0\\ g(x)\le 0\end{array}$$
$$（2）\sqrt{f(x)}\le g(x)⟺\{\begin{array}{l}f(x)\ge 0\\ g(x)\ge 0\\ g^2(x)\ge f(x)\end{array}$$
$$（3）\sqrt{f(x)}＞\sqrt{g(x)}⟺\{\begin{array}{l}f(x)\ge 0\\ g(x)\ge 0\\ f(x)＞g(x)\end{array}$$

指数、对数不等式——【】
遇到指数或对数不等式，结合单调性进行分析，或者换元转化为一般的不等式求解。
遇到对数不等式，要注意两个问题，一个是对数的定义域，另一个是对数的单调性。

柯西不等式——【遇到单独的平方和及混合项的平方时，在求二元（或多元）代数式最值或者二元（或多元）不等式证明时使用】
柯西不等式对于全体实数恒成立
二维柯西不等式：$(a^2+b^2)(c^2+d^2)\ge (ac+bd{)}^2$，当$ad=bc$或者$\frac{a}{c}=\frac{b}{d}$时，等号成立，两边相等。——【推导过程如下：$(a^2+b^2)(c^2+d^2)-(ac+bd{)}^2=a^2{c}^2+a^2{d}^2+b^2{c}^2+b^2{d}^2-(a^2{c}^2+2abcd+b^2{d}^2)=a^2{d}^2-2abcd+b^2{c}^2=(ad-bc{)}^2\ge 0，故(a^2+b^2)(c^2+d^2)\ge (ac+bd{)}^2$】
简化变形式：令$a=b=1$，$c=x$，$d=y$，则上述不等式变形为$2(x^2+y^2)\ge (x+y{)}^2$，当且仅当$x=y$时等号成立。——【可用于判断$x^2+y^2与x+y$的大小关系】
三维柯西不等式：$(a^2+b^2+c^2)(d^2+e^2+f^2)\ge (ad+be+cf{)}^2$，当$ae=bd=ce=bf$或者$\frac{a}{d}=\frac{b}{e}=\frac{c}{f}$时，等号成立，两边相等。

权方和不等式——【二元（或多元）的分式代数式求最值或不等式证明时使用】
$x＞0，y＞0，\frac{a^2}{x}+\frac{b^2}{y}\ge \frac{(a+b{)}^2}{x+y}$，当$\frac{a}{x}=\frac{b}{y}$时，等号成立

柯西不等式有$(a^2+b^2)(c^2+d^2)\ge (ac+bd{)}^2$，将其变形，易得$(\frac{a^2}{x}+\frac{b^2}{y})\cdot (x+y)\ge (a+b{)}^2$。在$a,b,x,y＞0$时，得：$\frac{a^2}{x}+\frac{b^2}{y}\ge \frac{(a+b{)}^2}{x+y}$，当$\frac{a}{x}=\frac{b}{y}$时，等号成立。并且权方和不等式也有多维形式：若$a_i＞0，b_i＞0，m＞0$，则$\frac{a_1^{m+1}}{b_1^m}+\frac{a_2^{m+1}}{b_2^m}+...+\frac{a_n^{m+1}}{b_n^m}\ge \frac{(a_1+a_2+...+a_n{)}^{m+1}}{(b_1+b_2+...+b_n{)}^m}$

——一元二次函数&一元二次方程&一元二次不等式——
注意：一元二次方程的根，即为相应一元二次函数的零点；一元二次不等式的解集，即为相应一元二次函数在x轴上方或下方的区域（有等号时包括零点)；一元二次不等式解集的端点，即为相应一元二次方程的根。

整体+局部

管理类联考——数学——汇总篇——知识点突破——代数——函数、方程、不等式——记忆——整体+局部