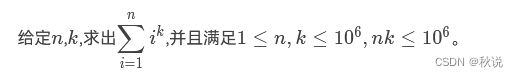【C/PTA】循环结构进阶练习（二）

本文结合PTA专项练习带领读者掌握循环结构，刷题为主注释为辅，在代码中理解思路，其它不做过多叙述。

7-1 二分法求多项式单根

二分法求函数根的原理为：如果连续函数f(x)在区间[a,b]的两个端点取值异号，即f(a)f(b)<0，则它在这个区间内至少存在1个根r，即f®=0。

二分法的步骤为：

• 检查区间长度，如果小于给定阈值，则停止，输出区间中点(a+b)/2；否则
• 如果f(a)f(b)<0，则计算中点的值f((a+b)/2)；
• 如果f((a+b)/2)正好为0，则(a+b)/2就是要求的根；否则
• 如果f((a+b)/2)与f(a)同号，则说明根在区间[(a+b)/2,b]，令a=(a+b)/2，重复循环；
• 如果f((a+b)/2)与f(b)同号，则说明根在区间[a,(a+b)/2]，令b=(a+b)/2，重复循环。

本题目要求编写程序，计算给定3阶多项式f(x)=a3x3+a2x2+a1x+a0在给定区间[a,b]内的根。

输入格式：

输入在第1行中顺序给出多项式的4个系数a3、a2、a1、a0，在第2行中顺序给出区间端点a和b。题目保证多项式在给定区间内存在唯一单根。

输出格式：

在一行中输出该多项式在该区间内的根，精确到小数点后2位。

输入样例：

3 -1 -3 1
-0.5 0.5

输出样例：

0.33

#include   
double a3, a2, a1, a0;  

double f(double x)  
{  
    double result;  
    result=a3*x*x*x+a2*x*x+a1*x+a0;  
    return result;  
}
  
int main()  
{  
    double a, b;  
    scanf("%lf%lf%lf%lf",&a3,&a2,&a1,&a0);  
    scanf("%lf%lf",&a,&b);  
    
    double left,mid,right;  
    left=a;  
    right=b;  
    
    ///大于阈值时使用二分法求出单根，程序结束
    while(right-left>=0.001&&f(left)*f(right)<=0)  
    {  
        if(f(left)==0)  
        {  
            printf("%.2f",left);  
            return 0;  
        }  
        if(f(right)==0)  
        {  
            printf("%.2f",right);  
            return 0;  
        }  
        
        mid=(left+right)/2;  
        if (f(mid)*f(left)>0)  
        {  
            left=mid;  
        }  
        else  //由于先决条件为f(left)*f(right)<0，因此此时else语句等价于f(mid)与f(left)异号，即与f(right)同号
        {  
            right=mid;  
        }  
    }  
    
    
    不大于阈值时输出中点
    printf("%.2f",mid);  
    return 0;  
}  

7-2 循环-十进制转化

小白龙新学了十进制的转换。现在他想把十进制数转化成其他进制的数，聪明的学弟学
妹们能帮帮他吗？因为小白龙还没有学习到数组，所以他希望这道题能够不用数组的相关知
识就可以解决。

输入格式:

输入只有两个整数N,M。 N ( 0 < N <= 100 ) 表示十进制数N。M（ 2 <= M <= 9 ）表示转换成M进制。

输出格式:

将N转化为M进制后然后输出。

输入样例:

在这里给出一组输入。例如：

50 4

输出样例:

在这里给出相应的输出。例如：

302

//题目暗示数组可以实现
#include 

int main() {
    int n,m,a[100],i=0;
    scanf("%d%d",&n,&m);
    
	while(n){
        a[i++] =n%m;  //从a[0]开始赋值
        n/=m;
    }
    
    while(i--){//逆序输出
        printf("%d",a[i]);
    }
}

7-3 梅森数

形如2n−1的素数称为梅森数（Mersenne Number）。例如2^2−1=3、23−1=7都是梅森数。1722年，双目失明的瑞士数学大师欧拉证明了231−1=2147483647是一个素数，堪称当时世界上“已知最大素数”的一个记录。

本题要求编写程序，对任一正整数n（n<20），输出所有不超过2n−1的梅森数。

输入格式：

输入在一行中给出正整数n（n<20）。

输出格式：

按从小到大的顺序输出所有不超过2n−1的梅森数，每行一个。如果完全没有，则输出“None”。

输入样例：

6

输出样例：

3
7
31

#include 
#include 

int f(int x)//判断素数的函数
{
	for(int i=2;i<=sqrt(x);i++)
	{
		if(x%i==0)
		return 0;//不是素数则返回0
	}
	return 1;
}


int main()
{
	int n;
	scanf("%d",&n);
	
	if(n<=1)//n<=1时一定不存在梅森数
	printf("None");  
	
	else//n>=2时一定存在梅森数
	{
		for(int i=2;i<=n;i++)
		{//对每一个2^i进行素数的判断
			int a=pow(2,i)-1;
			if(f(a))
			{
				printf("%d\n",a);
			}
		}
    }
}

7-4 单词长度

你的程序要读入一行文本，其中以空格分隔为若干个单词，以.结束。你要输出每个单词的长度。这里的单词与语言无关，可以包括各种符号，比如it's算一个单词，长度为4。注意，行中可能出现连续的空格；最后的.不计算在内。

输入格式：

输入在一行中给出一行文本，以.结束

**提示：**用scanf("%c",...);来读入一个字符，直到读到.为止。

输出格式：

在一行中输出这行文本对应的单词的长度，每个长度之间以空格隔开，行末没有最后的空格。

输入样例：

It's great to see you here.

输出样例：

4 5 2 3 3 4

如果题目要求不能出现连续的空格，以下代码是可行的：

#include 
int main()
{
	char c;
	int a=0;
	
	while((c=getchar())!='.')
	{
		if(c==' ')
		{
		printf("%d ",a);
		a=0;
		}
		else
		a++;
	}
	printf("%d",a);
}

但行中可能出现连续的空格，所以需要用一个标志变量来跟踪当前是否处于单词中的状态。

逻辑如下：

设count用于统计某单词的字符个数，mark用于标记是否遇到第一个空格，sum用于记录已经输出的单词个数。
如果当前字符不是空格，则将count加1
如果当前字符是空格并且count大于0，表示遇到一个单词的结束。
    如果mark大于0，说明不是第一个单词，先输出一个空格。
    输出统计得到的单词字符个数count。
    将sum加1，表示已经输出一个单词。
    将count重置为0，开始统计下一个单词的字符个数。
    将mark加1，表示已经遇到第一个空格。
循环结束后，判断最后一个单词是否有字符，如果有且sum大于0，输出最后一个单词的字符个数。

拿It's great to see you here.举例

初始状态：

• count = 0
• sum = 0
• mark = 0

字符 ‘I’:

• count = 1

字符 ‘t’:

• count = 2

字符 ‘’':

• count = 3

字符 ‘s’:

• count = 4

字符 ’ ':

输出4

• sgn=1

• cnt = 0

• mark = 1

字符 ‘g’:

• cnt = 1

字符 ‘r’:

• cnt = 2

字符 ‘e’:

• cnt = 3

字符 ‘a’:

• cnt = 4

字符 ‘t’:

• cnt = 5

字符 ’ ':

输出空格再输出5

• sgn=2

• cnt = 0

• mark = 2

字符 ‘t’:

• cnt = 1

字符 ‘o’:

• cnt = 2

字符 ’ ':

输出空格再输出2

• sgn=3

• cnt = 0

• mark = 3

字符 ‘s’:

• cnt = 1

字符 ‘e’:

• cnt = 2

字符 ‘e’:

• cnt = 3

字符 ’ ':

输出空格再输出3

• sgn=4

• cnt =0

• mark = 4

字符 ‘y’:

• cnt = 1

字符 ‘o’:

• cnt = 2

字符 ‘u’:

• cnt = 3

字符 ’ ':

输出空格再输出3

• sgn=5

• cnt = 0

• mark = 5

字符 ‘h’:

• cnt = 1

字符 ‘e’:

• cnt = 2

字符 ‘r’:

• cnt = 3

字符 ‘e’:

• cnt = 4

字符 ‘.’:

此时cnt > 0 && sgn > 0，输出4

最终程序输出的结果是：4 5 2 3 3 4

#include 

int main()
{
    char c;
    int count=0,mark=0,sum=0;

    while((c=getchar())!='.')
    {
        if(c!=' ')
            count++;
        else if(c==' '&&count>0)
        {
            if(mark>0)
            {
                printf(" ");
            }
            printf("%d",count);
            sum++;
            count=0;
            mark++;
        }
    }

    if(count>0&&sum>0)
    {
        printf(" %d",count);
    }
    else if(count>0&&sum==0)
    {
        printf("%d",count);
    }
    return 0;
}

7-5 21循环-求和3

sxtc爱做数学题，今天他又拿到一道数学题：

注意答案有可能很大，请对114514取模。

他希望擅长求和的你帮他解出这个求和问题。

输入格式:

读入两个数n,k。

输出格式:

输出求和结果，请对答案取模114514。

输入样例:

在这里给出一组输入。例如：

11451 4

输出样例:

在这里给出相应的输出。例如：

113968

思路：

1.使用两个嵌套的for循环，外层循环控制1到n的遍历，内层循环控制1到k的遍历。

2.在内层循环中，每次将total乘以当前外层循环的迭代变量i，并取结果对114514取模（%）。

3.在外层循环中，将计算得到的total累加到sum上，并将结果对114514取模，再重新将total置为1。

#include 
int main() {
    int n, k;
    scanf("%d%d", &n, &k);

    int total=1;
    int sum=0;

    for (int i=1;i<=n;i++) 
	{
        for (int j=1;j<=k;j++) 
		{
            total=(total*i)%114514;
        }
        sum =(sum+total)%114514;
        total=1;
    }
    printf("%d", sum);
}

7-6 21循环-金字塔

SeraphJACK正在摆积木。他想用这些积木垒成一座金字塔。同时摆好金字塔之后，他为每层积木涂上不同的颜色，这些颜色用从1开始的正整数表示，从最底层开始涂色。现在告诉你SeraphJACK有n块积木，请输出他用这些积木能摆出并涂色的最大金字塔。（金字塔形状详见样例,0表示这个位置没有积木）

输入格式:

一个整数n,1<=n<=1000

输出格式:

涂色后的金字塔

输入样例1:

在这里给出一组输入。例如：

11

输出样例1:

在这里给出相应的输出。例如：

0004000
0030300
0202020
1010101

输入样例2:

在这里给出一组输入。例如：

1

输出样例2:

在这里给出相应的输出。例如：

1

#include
int main()
{
    int sum,n,c=1,d;
    scanf("%d",&sum);
    
    for(n=1;n*(n+1)/2<=sum;n++);
    
    while(c<=(n-1))//外层循环控制层数
    {
        d=1;
        while(d<=2*n-3)//内层循环控制涂色及编号
        {
            if(d<=(n-1-c)||d>n-2+c)
                printf("0");
            //如果位置d小于等于(n-1-c)，或者大于n-2+c，则打印0。
            else if((d-n+1+c)%2==1)
                printf("%d",n-c);
            //否则，如果(d-n+1+c)除以2的余数为1，则打印n-c，表示涂上对应颜色的编号。
            else 
			printf("0");
            //否则，打印0。
            d++;
        }
        printf("\n");
        c++;
    }
    return 0;
}

7-7 循环-杨辉三角

Little VayH_E带着他的小伙伴玩起了杨辉三角的游戏…

输入格式:

输入包含两个正整数n和m(1<=n,m<=20)，两个数之间用空格分开。

输出格式:

输出杨辉三角的第n行与第m行之间（包含第n，m行）的部分，输出时注意：

倒数第一行的第一个数字前有0个空格…倒数第k行（如果有的话）的第一个数字前有k-1个空格…以此类推

每一行的每两个数字（如果有的话）之间有1个空格

每一行的最后一个数字后没有空格，在每一行的最后一个数字后输出一个换行符

对于所求的杨辉三角，每一个数字都只取最后一位，例如，若所求的杨辉三角上某个数字为10，则应输出0

输入样例:

在这里给出一组输入。例如：

1 4

输出样例:

在这里给出相应的输出。例如：

   1
  1 1
 1 2 1
1 3 3 1

#include 
int main()
{
	long int n,m,i,k,a,b,c,d,e,f,t;
	scanf("%ld %ld",&n,&m);
	if(n>m)
	{
		t=n;
		n=m;
		m=t;
	}
	
	for(i=n;i<=m;i++)//对于每行而言
	{
		for(k=m-i+1;k>1;k--)
		{
			printf(" ");//循环输出每行前面的空格
		}
		printf("1");
		for(a=1;a<=i-2;a++)//输出第i行的第二个到倒数第二个数
		{
			c=1;
			e=1;
			for(b=i-1;b>=i-a;b--)
			{
				c=c*b;
			}
			for(d=a;d>=1;d--)
			{
				e=e*d;
			}
			f=(c/e)%10;
			printf(" %ld",f);
		}
		if(i==1)
		printf("\n");//第一行输出回车
		else
		printf(" 1\n");//输出每行的最后一个1和回车
	}
	return 0;
}