霍特林模型
0 霍特林模型
在Hotelling模型中,产品在物质性能上是相同的,但在空间位置上有差异。因为不同位置上的消费者要支付不同的运输成本,他们关心的是价格与运输成本之和,而不单是价格。
1 情形1 商店位于两个端点
-
假定有一个长度为1的线性城市,消费者均匀地分布在[0,1]区间,分布密度为1。
-
假定在这个城市中有两个商店,分别位于城市的两端,商店1在 x = 0 x=0 x=0,商店2在 x = 1 x=1 x=1,出售物质性能相同的产品。
-
假定每个商店提供单位产品的成本为 c c c,消费者购买商品的旅行成本与离商店的距离成比例,单位距离的成本为 t t t。(这意味着住在 x x x的消费者如果在商店1采购,要花费 t x tx tx的旅行成本;如果在商店2采购,要花费 t ( 1 − x ) t(1-x) t(1−x)的旅行成本)
-
假定消费者只愿意购买一个商品,这个商品会给他们带来 U U U的效用,而为了购买这个商品消费者将会付出走到商店的旅行成本+购买产品的成本,因此最终效用可以表示为 U − 旅 行 成 本 − 商 品 价 格 U-旅行成本-商品价格 U−旅行成本−商品价格
-
假定 U U U足够使得 U − 旅 行 成 本 − 商 品 价 格 > 0 U-旅行成本-商品价格>0 U−旅行成本−商品价格>0,从而每个消费者都有意愿去购买一个单位的商品。
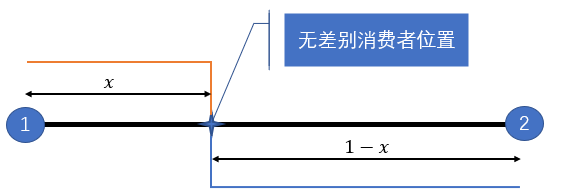
令 p i p_i pi为商店 i i i的价格, D i ( p 1 , p 2 ) D_i(p_1,p_2) Di(p1,p2)为需求函数, i = 1 , 2 i=1,2 i=1,2。如果住在 x x x的消费者在两个商店之间是无差异的(即他不介意在任何一家商店购买产品,在两个商店购买商品的最终效用相等)。那么,所有住在 x x x左边的将都在商店1购买,而住在 x x x右边的将在商店2购买,需求分别为 D 1 = ∫ 0 x 1 d x = x D_1=\int _0^{x}1dx = x D1=∫0x1dx=x, D 2 = ∫ x 1 1 d x = 1 − x D_2=\int _x^{1}1dx = 1-x D2=∫x11dx=1−x。(这里被积函数为1是因为假定1即分布密度为1)
此时, x x x应满足
p 1 + t x = p 2 + t ( 1 − x ) (1) p_1 + t x=p_2 + t (1-x) \tag{1} p1+tx=p2+t(1−x)(1)
解得
D 1 ( p 1 , p 2 ) = x = 1 2 + p 2 − p 1 2 t D 2 ( p 1 , p 2 ) = 1 − x = 1 2 + p 1 − p 2 2 t (2) D_1(p_1,p_2)=x=\frac{1}{2}+\frac{p_2-p_1}{2t}\\ D_2(p_1,p_2)=1-x=\frac{1}{2}+\frac{p_1-p_2}{2t} \tag{2} D1(p1,p2)=x=21+2tp2−p1D2(p1,p2)=1−x=21+2tp1−p2(2)
理解:若两商店的产品价格相同(即 p 2 = p 1 = p p_2 = p_1=p p2=p1=p)那么无差别消费者的位置为两商店的中间位置,此时无论是去商店1购买还是去商店2购买总成本都等于 p + t 2 p + \frac{t}{2} p+2t,因此两商店平分市场份额。若 p 2 > p 1 p_2>p1 p2>p1那么无差别消费者的位置将会向右移动,这是因为消费者2涨价后,若无消费者还是停留在涨价前的位置,那么此时显然消费者去商店1消费商品的最终效用更大。为了平衡商店2涨价后的影响,涨价前无差别消费者的位置将会右移,同理 p 1 > p 2 p_1>p_2 p1>p2。 t t t在这里作为移动距离的比例因子存在。
商店1的利润函数为:
π 1 ( p 1 , p 2 ) = ( p 1 − c ) D 1 ( p 1 , p 2 ) = 1 2 ( p 1 − c ) + 1 2 t ( p 1 − c ) ( p 2 − p 1 ) (3) \pi_1(p_1,p_2)=(p_1-c)D_1(p_1,p_2)\\ =\frac{1}{2}(p_1-c) + \frac{1}{2t}(p_1-c)(p_2-p_1) \tag{3} π1(p1,p2)=(p1−c)D1(p1,p2)=21(p1−c)+2t1(p1−c)(p2−p1)(3)
商店2的利润函数为:
π 2 ( p 1 , p 2 ) = ( p 2 − c ) D 2 ( p 1 , p 2 ) = 1 2 ( p 2 − c ) + 1 2 t ( p 2 − c ) ( p 1 − p 2 ) (4) \pi_2(p_1,p_2)=(p_2-c)D_2(p_1,p_2)\\ =\frac{1}{2}(p_2-c) + \frac{1}{2t}(p_2-c)(p_1-p_2) \tag{4} π2(p1,p2)=(p2−c)D2(p1,p2)=21(p2−c)+2t1(p2−c)(p1−p2)(4)
商店 i i i选择自己的价格 p i p_i pi最大化利润 π i \pi_i πi,给定 p j p_j pj,两个一阶条件分别是
∂ π 1 ∂ p 1 = 0 − − > p 2 + c + t − 2 p 1 = 0 ∂ π 2 ∂ p 2 = 0 − − > p 1 + c + t − 2 p 2 = 0 (5) \frac{\partial \pi_1}{\partial p_1} = 0 -->p_2 + c + t - 2p_1 = 0\\ \frac{\partial \pi_2}{\partial p_2} = 0 -->p_1 + c + t - 2p_2 = 0 \tag{5} ∂p1∂π1=0−−>p2+c+t−2p1=0∂p2∂π2=0−−>p1+c+t−2p2=0(5)
解得
p 1 ∗ = p 2 ∗ = c + t (6) p_1^{*} = p_2^{*} = c + t \tag{6} p1∗=p2∗=c+t(6)
每个商店的均衡利润为:
π 1 ∗ = π 2 ∗ = t 2 (7) \pi_1^{*} = \pi_2^{*} = \frac{t}{2} \tag{7} π1∗=π2∗=2t(7)
将消费者的位置差异解释为产品差异,这个差异进一步可解释为消费者购买产品的旅行成本。旅行成本越高,产品的差异就越大,均衡价格就越大从而均衡利润也就越高。原因在于,随着旅行成本的上升,不同商店出售的产品之间的替代性下降,每个商店对附近的消费者的垄断力加强,商店之间的竞争越来越弱,消费者对价格的敏感度下降,从而每个商店的最优价格更接近于垄断价格。另一方面,当旅行成本为零时( t = 0 t=0 t=0),不同商店的产品之间具有完全的替代性,没有任何一个商店可以把价格定得高于成本,我们得到伯川德均衡结果。
2 情形2 两个商店位于同一个位置
假定两个商店位于同一个位置 x x x。此时,他们出售的是同质的产品,消费者关心的只是价格,那么伯川德均衡是唯一的均衡:
p 1 = p 2 = c , π 1 = π 2 = 0 (8) p_1 = p_2 = c,\pi_1 = \pi_2 = 0 \tag{8} p1=p2=c,π1=π2=0(8)
3 情形3 两个商店位于不同位置
-
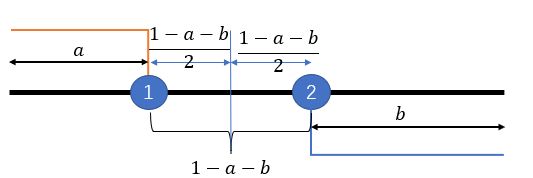
假定商店1位于 a ≥ 0 a\ge 0 a≥0,商店2位于 1 − b 1 - b 1−b( b ≥ 0 b\ge 0 b≥0)。
-
假定旅行成本为二次式,即旅行成本为 t d 2 td^2 td2, d d d表示消费者到商店的距离。
同情形1假定无差别消费者的位置为 x x x,显然 a ≤ x ≤ 1 − a − b a\le x \le 1-a-b a≤x≤1−a−b即无差别消费者位于两个商店之间。此时无差别消费者去商店1和去商店2购买1单位商品的最终效用相同,因此我们可以得到如下等式:
p 1 + t ( x − a ) 2 = p 2 + t ( 1 − b − x ) 2 (9) p_1 + t (x - a)^2 = p_2 + t (1 - b - x)^2 \tag{9} p1+t(x−a)2=p2+t(1−b−x)2(9)
解得无差别消费者的位置为:
x = a + 1 − a − b 2 + p 2 − p 1 2 t ( 1 − a − b ) (10) x = a + \frac{1-a-b}{2} + \frac{p_2-p_1}{2t(1-a-b)}\tag{10} x=a+21−a−b+2t(1−a−b)p2−p1(10)
显然无差别消费者左侧的市场份额全属于商店1,无差别消费者右侧的市场份额全属于商店2,因此我们得到两商店的需求函数如下:
D 1 ( p 1 , p 2 ) = x = a + 1 − a − b 2 + p 2 − p 1 2 t ( 1 − a − b ) D 2 ( p 1 , p 2 ) = 1 − x = b + 1 − a − b 2 + p 1 − p 2 2 t ( 1 − a − b ) (11) D_1(p_1,p_2) = x = a + \frac{1-a-b}{2} + \frac{p_2-p_1}{2t(1-a-b)}\\ D_2(p_1,p_2) = 1 - x = b + \frac{1-a-b}{2} + \frac{p_1-p_2}{2t(1-a-b)} \tag{11} D1(p1,p2)=x=a+21−a−b+2t(1−a−b)p2−p1D2(p1,p2)=1−x=b+21−a−b+2t(1−a−b)p1−p2(11)
理解:如果两个商店的商品价格一样即 p 2 = p 1 p_2=p_1 p2=p1,那么无差别消费者仍然位于两商店的中间位置(注意:此时无差别消费者的位置并不一定位于线性城市的中间位置),在两商店中间位置的基础上根据价格和旅行成本进行调整。
根据商店的利润函数(3)(4)及其一阶条件(5)求得纳什均衡为:
p 1 ∗ ( a , b ) = c + t ( 1 − a − b ) ( 1 + a − b 3 ) p 2 ∗ ( a , b ) = c + t ( 1 − a − b ) ( 1 + b − a 3 ) (12) p_1^{*}(a,b) = c + t ( 1 - a - b)( 1 + \frac{a - b}{3})\\ p_2^{*}(a,b) = c + t ( 1 - a - b)( 1 + \frac{b - a}{3}) \tag{12} p1∗(a,b)=c+t(1−a−b)(1+3a−b)p2∗(a,b)=c+t(1−a−b)(1+3b−a)(12)
当 a = b = 0 a = b = 0 a=b=0时,商店1位于0,商店2位于1此时回到情形1:
p 1 ∗ ( 0 , 1 ) = p 2 ∗ ( 0 , 1 ) = c + t (13) p_1^{*}(0,1) = p_2^{*}(0,1) = c + t \tag{13} p1∗(0,1)=p2∗(0,1)=c+t(13)
当 a = 1 − b a = 1 - b a=1−b时,两个商店位于同一位置,此时回到情形2:
p 1 ∗ ( a , 1 − a ) = p 2 ∗ ( a , 1 − a ) = c (14) p_1^{*}(a,1-a) = p_2^{*}(a,1-a)=c \tag{14} p1∗(a,1−a)=p2∗(a,1−a)=c(14)