基于顺序结构和单链表的各种排序算法C++实现
一、插入排序
(减治法思想 decrease-and-conquer)
1.直接插入排序 Straight Insertion Sort
Insertion sort
时间复杂度O(n^2) quadratic sorting algorithms
空间复杂度O(1) In-place; i.e., only requires a constant amount O(1) of additional memory space
稳定:不会改变相等元素的相对位置。 Stable; i.e., does not change the relative order of elements with equal keys
适用于顺序存储和链式存储。
Insertion sort iterates(迭代), consuming one input element each repetition, and grows a sorted output list. At each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list, and inserts it there. It repeats until no input elements remain.
算法描述: L[1…n]
初始L[1]是一个已经排好序的子序列;
将L(i)(L[2…n])插入到已排好序的子序列 :
(1)查找出L(i)在L[1…i-1]中的位置k;
(2)将L[k…i-1]中的所有元素后移一位;
(3)将L(i)复制到L(k)
基于顺序存储的直接插入排序:
//直接插入排序(顺序存储)
void straisort(vector<int>& array) {
int i, j;
//把数组分为有序序列array[1...i-1]和无序序列array[i...n]
for (i = 2; i < array.size(); ++i) {
//array[0]设为哨兵(array[0]不存储待排序元素),其作用是(1)可减少一个条件判断(是否比较到最后一个元素);
//(2)保存待插入的元素,不用再申请额外空间
/*这里可以加个判断:if (array[i] < array[i - 1])当array[i]>array[i-1]时说明不用插入,啥也不做:
for (i = 2; i < array.size(); ++i) {
if (array[i] < array[i - 1]) {
array[0] = array[i];
for (j = i - 1; array[j] > array[0]; --j) {
array[j + 1] = array[j];
}
array[j + 1] = array[0];
}
}*/
array[0] = array[i];
//从i-1往左依次比较寻找合适的插入位置,移动元素
//注意这里的判断条件是array[j]>array[0]而非array[j]>array[i],因为array[i]会被array[j + 1]覆盖
for (j = i - 1; array[j] > array[0]; --j) {
array[j + 1] = array[j];
}
//插入元素i,array[0]存储的即为array[i].
array[j + 1] = array[0];
}
}
注意:若不使a[0]作哨兵,则需加判段j>=0,并且必须是j >= 0&&nums[j] > tmp而不能写nums[j] > tmp&&j >= 0,否则数组下标越界!!!
void sort(vector<int>& nums) {
//插入排序
int i, j, tmp;
for (i = 1; i < nums.size(); ++i) {
tmp = nums[i];
for (j = i - 1; j >= 0&&nums[j] > tmp; j--) {
nums[j + 1] = nums[j];
}
nums[j + 1] = tmp;
}
}
int main()
{
vector<int> array({ 0,6,4,63,55,54,75,18,9,6 });
straisort(array);
for (int i = 1;i<array.size();++i ){
cout << array[i] << ' ';
}
cout << endl;
}
基于链式存储的直接插入排序:
typedef struct Listnode {
int val;
Listnode* next;
Listnode() { ; }
Listnode(int x) : val(x), next(NULL) {}
}linkList;
//创建链表
linkList* creatlist() {
linkList* head = new linkList(0);
linkList* node;
int num;
cout << "input(end with 0):" << endl;
cin >> num;
while (num != 0) {
node = new linkList();
node->val = num;
node->next = head->next;
head->next = node;
cin >> num;
}
return head;
}
//直接插入排序(链式存储)
void straisort(linkList* head) {
if(head->next==NULL||head->next->next==NULL){
return head;
}
//同样将链表分为有序序列pCur和无序序列qCur, 有序序列含表头节点
//初始链表中第一个节点为有序子序列,后面的节点为无序子序列,将其依次插入到有序子序列
linkList* pPre, *pCur, *qPre, *qCur;
pPre = head;
pCur = head->next;
qCur = pCur->next;
pCur->next = NULL;
//遍历无序子序列
while (qCur) {
//每次都要重置pPre和pCur,以便从有序链表的第一个节点查找插入点
pPre = head;
pCur = head->next;
//寻找合适的插入位置
while (pCur) {
if (qCur->val < pCur->val) {
break;
}
else {
//qCur->val大于等于pCur->val,则记录pPre并将其右移
pPre = pCur;
pCur = pCur->next;
}
}
//插入前的准备动作:已找到插入位置,则记录qCur并将qCur右移
qPre = qCur;
qCur = qCur->next;
//插入到相应位置: pCur之前,pPre之后
qPre->next = pCur;
pPre->next = qPre;
}
}
int main()
{
linkList *head = creatlist();
straisort(head);
linkList* p = head->next;
while (p) {
cout << p->val << ' ';
p = p->next;
}
cout << endl;
}
2.折半插入排序 Binary Insertion Sort
Binary insertion sort employs a binary search to determine the correct location to insert new elements, and therefore performs ⌈log2 n⌉ comparisons in the worst case, which is O(n log n). The algorithm as a whole still has a running time of O(n2) on average because of the series of swaps required for each insertion.
是直接插入排序的优化,引入折半查找替代顺序查找,减少关键字间的比较次数。
只适用于顺序存储。
由于仅减少了关键字间的比较次数,记录的移动次数不变,因而其时间复杂度仍为O(n^2), 空间复杂度O(1).
void straisort(vector<int>& array) {
int i, j;
int low, mid, high;
//依次将无序序列中的元素插入有序序列
for (i = 2; i < array.size(); ++i) {
array[0] = array[i];
low = 1; high = i - 1;
//折半查找
while (low <= high) {
mid = (low + high) / 2;
if (array[mid] <= array[i]) { //等于时要插到其后面,保证排序的稳定性
low = mid + 1;
}
else {
high = mid - 1;
}
}
//折半查找已找到插入位置,此时仅需移动元素腾出插入位置
for (j = i - 1; j > high; --j) {
array[j + 1] = array[j];
}
//插入
array[high + 1] = array[0]; //== array[low] = array[0];
}
}
int main()
{
vector<int> array({ 0,6,4,63,55,54,75,18,9,6 });
straisort(array);
for (int i = 1;i<array.size();++i ){
cout << array[i] << ' ';
}
cout << endl;
}
3.希尔排序 Shell sort
Shellsort is an optimization of insertion sort that allows the exchange of items that are far apart.
又称缩小增量排序。
图解排序算法之希尔排序

增量的选取:
![]()
时间复杂度:最坏为O(n^2)
空间复杂度:O(1)
适用于顺序存储,因为要对数组下标进行操作。
//希尔排序
void shellsort(vector<int>& a) {
int n = a.size() - 1;//n为待排序元素总数,因为数组中a[0]作哨兵用
//dk为增量,每次缩减一半,最后一次循环dk=1,对整个数组直接插入排序
for (int dk = n / 2; dk >= 1; dk = dk / 2) {
//这里并不是按照每一趟排一组子序列,而是同时对所有子序列排序,即每循环一次++i,就是对下一组子序列的排序
//依然是把每组子序列分为有序和无序,将无序序列依次插入有序序列
int i,j;
for (i = dk + 1; i <= n; ++i) {
if (a[i] < a[i - dk]) { //a[i]>a[i-dk]时什么也不用做
a[0] = a[i];
for (j = i - dk; j > 0 && a[j] > a[0];j-=dk) {
a[j + dk] = a[j];
}
a[j + dk] = a[0];
}
}
}
}
int main()
{
vector<int> array({ 0,4,6,63,55,54,75,18,9,6 });
shellsort(array);
for (int i = 1;i<array.size();++i ){
cout << array[i] << ' ';
}
cout << endl;
}
二、交换排序
4.冒泡排序 Bubble sort
Bubble sort is a simple sorting algorithm that repeatedly steps through the list, compares adjacent elements and swaps them if they are in the wrong order. The pass through the list is repeated until the list is sorted.
The only significant advantage that bubble sort has over most other algorithms, even quicksort, but not insertion sort, is that the ability to detect that the list is sorted efficiently is built into the algorithm. When the list is already sorted (best-case), the complexity of bubble sort is only O(n).
基本思想: 假设待排序表长为n,从后往前(从前往后)两两比较相邻元素的值,若为逆序(即A[i-1]>A[i]),则交换他们直到序列比较结束。(默认升序排列)
一趟冒泡排序会将一个元素放在它最终的位置上。进行n-1趟冒泡排序即可完成排序。
时间复杂度:
最好:序列有序,O(n)
最坏:比较次数为 ∑ 1 n − 1 ( n − i ) \sum_1^{n-1}(n-i) ∑1n−1(n−i) = n(n-i)/2 , O(n^2)
平均:O(n^2) Bubble sort has a worst-case and average complexity of О(n ^2)
空间复杂度: O(1)
适用于顺序存储和链式存储: 主要是元素的比较和交换,不涉及数组下标的操作,在链表中比较和交换也很容易。
稳定!
基于顺序存储:
//冒泡排序(基于顺序存储)
void BubbleSort(vector<int>& a) {
int n = a.size();
//n-1趟冒泡
for (int i = 0; i < n - 1; ++i) {
bool flag = false;
//从前往后两两比较,每趟n-i次
for (int j = 1; j < n-i; ++j) {
if (a[j - 1] > a[j]) {
swap(a[j - 1], a[j]);
flag = true;
}
}
//如果在n-1趟排序之前已完成排序,可直接退出。因为在每趟排序时只有发生了元素交换才会使flag=true
//所以在某趟排序中若无元素交换,则说明已完成排序
if (flag == false) {
return;
}
}
}
int main()
{
vector<int> array({ 0,4,6,63,55,54,75,18,9,6 });
BubbleSort(array);
for (int i = 0;i<array.size();++i ){
cout << array[i] << ' ';
}
cout << endl;
}
基于链式存储:
//冒泡排序(基于链式存储)
void BubbleSort(linkList* head) {
linkList* p, * q;
for (int i = 0; i < head->val - 1; ++i) {
q = head->next;
p = q->next;
bool flag = false;
//每趟n-i次比较
for (int j = 1; j < head->val - i; ++j) {
if (p->val < q->val) {
int tmp = p->val;
p->val = q->val;
q->val = tmp;
flag = true;
}
p = p->next;
q = q->next;
}
if (flag == false) {
return;
}
}
}
int main()
{
linkList* head = creatlist();
linkList* p = head->next;
while (p) {
cout << p->val << ' ';
p = p->next;
}
cout << endl;
BubbleSort(head);
p = head->next;
while (p) {
cout << p->val << ' ';
p = p->next;
}
cout << endl;
}
5.快速排序 quicksort
也称分区交换排序( partition-exchange sort),或Hoare排序。1962年首先由霍尔(C.A.R.Hoare)提出。
是至今为止内部(比较)排序中较快的一种。它有广泛的应用,典型的应用是UNIX系统调用库函数例程中的qsort函数。但快速排序往往由于最差时间代价的性能而在某些应用中无法采用。
Quicksort is a divide-and-conquer algorithm. It works by selecting a ‘pivot’ element from the array and partitioning the other elements into two sub-arrays, according to whether they are less than or greater than the pivot. The sub-arrays are then sorted recursively(递归). This can be done in-place, requiring small additional amounts of memory to perform the sorting.
On average, the algorithm takes O(n log n) comparisons to sort n items. In the worst case, it makes O(n2) comparisons, though this behavior is rare.
基本思想: 通过一趟排序将待排序记录分割为独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
一趟排序的基本思路:选任意记录作枢轴(pivot),将所有关键字比它小的记录放到它之前,比它大的放到它之后。
一趟排序会将一个元素pivot放在它最终的位置上。

尤其适合于初始有序状态最差的情况。主要特点是采取了分治的思想,递归实现。
划分的过程的正确性证明:
先任选一个枢轴,这里取第一个元素,记为t;两个指针i,j,初始位置分别位于需要划分的数组的头部和尾部。i只能递增,j只能递减。
当i与j不重合时,反复执行如下步骤(下面的叙述中,“副本”指的是从一个元素复制出来的与该元素完全相同的实例。如果待排序的数组本来就有多个完全相同的元素,那么将这些元素都看成互相不同的,而不是互相视为副本):
【1】从右往左查找第一个小于枢轴t的元素(查找时j递减)。找到后执行【2】,否则继续查找。
【2】* i = * j,即将找到的小于枢轴的元素放到左侧,产生了一个找到的元素的副本。
【3】从左往右查找第一个大于枢轴t的元素(查找时i递增)。找到后执行【4】,否则继续查找。
【4】* j = * i,即将找到的大于枢轴的元素放到右侧,产生了一个找到的元素的副本。
每次将小于或大于枢轴的元素移到对面后,被放到对面的元素在数组中会含有一个副本,副本写入的位置原有的元素被覆盖。执行这种操作时:
(1)如果是第一次执行,那么i一定位于初始位置,即枢轴的位置,且枢轴会被用j指向的元素覆盖(即执行的一定是步骤【2】)。不可能先将左侧的元素写入j指向的位置。因为已经规定“从右往左查找第一个小于枢轴t的元素”这一步(即步骤【1】)先进行。也就是说,j递减到找到一个小于枢轴t的元素,或与i重合时,才会停止递减。这时候要么i = j,此时步骤【2】和【4】等效于不执行(因为是自己覆写自己),然后因为外层循环的i≠j的条件不再符合,外层循环会被退出;要么仍有i≠j,此时i指向的元素(即枢轴)被替换为j指向的元素。
(2)如果不是第一次执行,原先重复的元素的其中一个副本会被新的找到的符合条件的元素覆盖。这个新的元素在数组里也有两个,一个是原有的,一个是新的副本。
(1)(2)告诉我们:无论在什么时候执行具有覆写效果的步骤【2】或【4】,数组中始终只有一个元素具有副本。且原数组中只有被选为枢轴的元素会丢失。
当i,j重合后,执行*i = t,此时枢轴覆盖了最后一个,也是唯一一个具有副本的元素的副本。
因为第一次执行步骤【2】后,枢轴就被j指向的元素覆盖了。为了确保枢轴不丢失,就需要用一个临时变量t将枢轴暂时保存。
步骤【2】和【4】分别总是把小于或大于枢轴的元素移到对面。由于i和j分别是递增、递减的,因此在i = j后,i,j重合的位置的左侧全部是小于枢轴的元素,右侧全部是大于枢轴的元素。这就证明了划分过程的正确性。
最好、平均时间复杂度: O( n l o g 2 n ) nlog_2n) nlog2n),每一层移动的次数为O(n)数量级。
最好、平均空间复杂度: O( l o g 2 n ) log_2 n) log2n), 递归栈空间。
最坏时间复杂度:初始记录序列按关键字有序或基本有序时,蜕化为冒泡排序,O(n^2).
最坏空间复杂度:O(n) 栈的最大深度n:每趟排序后,pivot的位置都偏向子序列的一端。
一般为O(logn)
最坏的情况是每次都只能将长度为k的数组划分为枢轴、长为0的子数组和长为k – 1的子数组。每加深一层递归时,较长的子数组的长度只减1。这时递归深度为n。所以,快速排序的最坏情况的时间复杂度为O(n^2)。
不稳定。 it is not a stable sort.
适用于顺序存储(链式存储)。
快排的应用实例:
https://leetcode-cn.com/problems/kth-largest-element-in-an-array/
快排思想变形应用: https://leetcode-cn.com/problems/sort-colors/solution/
基于顺序存储的快排:
//快速排序(基于顺序存储)
void QuickSort(vector<int>& a, int low, int high) {
int i = low, j = high;
int pivot = a[i]; //选第一个元素作为枢轴
while (i < j) {
while (i < j && pivot <= a[j]) {//从右往左搜索小于pivot的元素并将其放到pivot左边
j--;
}
a[i] = a[j];//此a[high]
while (i < j && pivot >= a[i]) {//从左往右找大于pivot的元素,将其放到右边
i++;
}
a[j] = a[i];
}
a[i] = pivot; //i=j
//上面实现一趟快排,下面递归实现枢轴两边序列的快排
if (low < j) {
QuickSort(a, low, j - 1);
}
if (high > i) {
QuickSort(a, i + 1, high);
}
}
int main()
{
vector<int> array({ 0,4,6,63,55,54,75,18,9,6 });
QuickSort(array, 0, array.size()-1);
for (int i = 0;i<array.size();++i ){
cout << array[i] << ' ';
}
cout << endl;
}
基于链式存储的快排:
单链表的快排序和数组的快排序基本思想相同,同样是基于划分,但是又有很大的不同:单链表不支持基于下标的访问。可以采用一趟遍历的方式,通过改变节点的指针,将小于枢轴节点值的元素以头节点连到枢轴节点的左边,将大于枢轴节点的元素连到枢轴节点右边,枢轴节点作为两部分的桥梁,这样就实现了一趟快排,然后递归快排左右两边的子链表。
//快速排序(基于单链表)
//head为(带头节点的)单链表头节点指针,tail为单链表尾节点的next指针指向的内容。
//通常情况下tail的内容为NULL,因此,调用时为QuickSort(head, NULL)。
void QuickSort(linkList* head, linkList* tail) {
//递归调用出口
if (head->next == tail || head->next->next == tail) {
return;
}
linkList* pivot = head->next; //枢轴节点
linkList* p = head;
linkList* q = pivot;
linkList* pCur = pivot->next;
while (pCur != tail) {
//把小于pivot的节点连到头节点上
if (pCur->val < pivot->val) {
p->next = pCur;
p = pCur;
}
//把大于pivot的节点连到pivot上
else {
q->next = pCur;
q = pCur;
}
pCur = pCur->next;
}
//用pivot把两边连起来
p->next = pivot;
q->next = tail;
//递归快排两边子链表
QuickSort(head, pivot);
QuickSort(pivot, tail);
}
int main()
{
linkList* head = creatlist();
linkList* p = head->next;
while (p) {
cout << p->val << ' ';
p = p->next;
}
cout << endl;
QuickSort(head,NULL);
p = head->next;
while (p) {
cout << p->val << ' ';
p = p->next;
}
cout << endl;
}
三、选择排序 Selection sort
基本思想: 每一趟在n-i+1个记录中选取关键字最小的记录作为有序序列中第i个记录,直到n-1趟做完,待排序元素只剩一个。
一趟排序会将一个元素放在它最终的位置上。
6.简单(直接)选择排序
The algorithm divides the input list into two parts: a sorted sublist of items which is built up from left to right at the front (left) of the list and a sublist of the remaining unsorted items that occupy the rest of the list. Initially, the sorted sublist is empty and the unsorted sublist is the entire input list. The algorithm proceeds by finding the smallest (or largest, depending on sorting order) element in the unsorted sublist, exchanging (swapping) it with the leftmost unsorted element (putting it in sorted order), and moving the sublist boundaries one element to the right.

不稳定。
时间复杂度:(最好、最坏、平均)O(n^2). 与初始序列无关,比较次数均为n(n-1)/2 。
空间复杂度: O(1).
适用于顺序存储和链式存储。
//直接选择排序
void smp_selectSort(vector<int>& a) {
//n-1趟选择排序
for (int i = 0; i < a.size() - 1; ++i) {
int min = i;
for (int j = i + 1; j < a.size(); ++j) {
if (a[j] < a[min]) {
min = j;
}
}
if (min != i) {
swap(a[min], a[i]);
}
}
}
int main()
{
vector<int> array({ 0,4,6,63,55,54,75,18,9,6 });
smp_selectSort(array);
for (int i = 0;i<array.size();++i ){
cout << array[i] << ' ';
}
cout << endl;
}
7.堆排序 Heapsort
克服了树形选择排序的缺陷。
堆排序是不稳定的. 适合于大量记录情况。 it is not a stable sort.
Heapsort can be thought of as an improved selection sort: like selection sort, heapsort divides its input into a sorted and an unsorted region, and it iteratively shrinks the unsorted region by extracting the largest element from it and inserting it into the sorted region. Unlike selection sort, heapsort does not waste time with a linear-time scan of the unsorted region; rather, heap sort maintains the unsorted region in a heap data structure to more quickly find the largest element in each step.
时间复杂度:最坏、平均O( n l o g 2 n ) nlog_2n) nlog2n). 平均时间性能比快速排序要差一些(相差系数)。最坏情况比快速排序好的多,这是堆排序相对于快排的最大优点。
空间复杂度:O(1).
适用于顺序存储和链式存储。
步骤一 构造初始堆。将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆)。
步骤二 将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。

即对所有非终端节点按编号从大到小调整,最后一个非终端节点为第n/2个元素。
//筛选:自上至下调整(小根堆)
//k表示从编号为k的节点开始调整,len表示参与调整的元素编号大小范围
//a[k+1..len]中元素满足堆的性质,此函数调整a[k]使整个a[k..len]中元素满足堆的性质
void sift(vector<int>& a, int k, int len) {
int i = k * 2;
a[0] = a[k]; //存a[k]的副本,这样就可以在最终找到k的位置后将其填入,不用每次循环都交换a[k]和a[i]
bool finish = false;
while (i <= len && !finish) {
//若存在右子树(j+1<=len)且右子树根的关键字小,则沿右分支“筛选”
if (i<len && a[i]>a[i + 1]) {
i = i + 1;
}
//由于a[k+1..len]中各元素满足堆的性质,当发现a[k]<=a[j]时,说明整个序列已满足堆,筛选完毕
if (a[0] <= a[i]) {
finish = true;
}
else { //继续筛选
a[k] = a[i];
k = i;
i = k * 2; //i的左孩子
}
}
a[k] = a[0]; //a[k]填入恰当的位置
}
void heapsort(vector<int>& a,int len) {
//创建堆 从一个无序序列建堆的过程就是一个反复筛选的过程
//从最后一个非终端节点len/2开始筛选
for (int i = len / 2; i > 0; --i) {
sift(a, i, len);
}
//每次输出堆顶元素并筛选重新建堆
for (int i = len; i > 1; --i) {
swap(a[1], a[i]); //将堆顶元素和堆中最后一个元素交换
sift(a, 1, i - 1); //从堆顶向下调整使a[1..i-1]变为堆,这里每次已输出的元素(交换到后面的)不再参与调整
}
}
int main()
{
vector<int> array({ 0,4,6,63,55,54,75,18,9,6 });
heapsort(array,array.size()-1);
for (int i = 1;i<array.size();++i ){
cout << array[i] << ' ';
}
cout << endl;
}
堆排序应用实例:
https://leetcode-cn.com/problems/kth-largest-element-in-an-array/
priority_queue的使用与堆的实现
拜托,面试别再问我TopK了!!!
703. 数据流中的第 K 大元素
四、归并排序
8.归并排序 Merge sort
https://editor.csdn.net/md/?articleId=108419773
Conceptually, a merge sort works as follows:
Divide the unsorted list into n sublists, each containing one element (a list of one element is considered sorted).
Repeatedly merge sublists to produce new sorted sublists until there is only one sublist remaining. This will be the sorted list.
核心思想:归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案”修补”在一起,即分而治之)。
时间复杂度:(最好、最坏、平均)O( l o g 2 n log_2n log2n), 每次合并操作的平均时间复杂度为O(n) ,需进行 l o g 2 n log_2n log2n趟归并。
空间复杂度:O(n) 需要和待排序记录等数量的辅助空间
稳定!
适用于顺序存储和链式存储。
基于顺序结构的归并排序:
//二路归并排序(基于顺序存储)
void Merge(vector<int>& a,int low,int mid,int high) {
//第一步,申请辅助空间,大小为两个排序序列之和
vector<int> b(high - low + 1);
//第二步,设定两个待排序列的起始位置的索引和辅助空间的索引(0)
int i = low, j = mid + 1, k = 0;
while (i <= mid && j <= high) {
if (a[i] <= a[j]) {
b[k++] = a[i++];
}
else {
b[k++] = a[j++];
}
}
while (i <= mid) {
b[k++] = a[i++];
}
while (j <= high) {
b[k++] = a[j++];
}
//将合并且排序好的元素,复制到原来的数组中,释放临时数组空间
for (int i = 0; i < k; ++i)
a[low + i] = b[i];
b.clear();
}
void MergeSort(vector<int>& a,int low, int high) {
if (low < high) {
int mid = (low + high) / 2;
MergeSort(a, low, mid);
MergeSort(a, mid + 1, high);
Merge(a, low, mid, high);
}
}
int main()
{
vector<int> a({ 0,4,6,63,55,54,75,18,9,6 });
MergeSort(a, 0, a.size() - 1);
for (int i = 0;i<a.size();++i ){
cout << a[i] << ' ';
}
cout << endl;
}
另一种更好的写法:
void mergesort(vector<int>& nums, int low, int high, vector<int>& tmp) {
if (low >= high) {
return;
}
//divede
int mid = (low + high) / 2;
mergesort(nums, low, mid, tmp);
mergesort(nums, mid + 1, high, tmp);
//conquer
int i = low, j = mid+1, k = low;
while (i <= mid && j <= high) {
if (nums[i] <= nums[j]) {
tmp[k++] = nums[i++];
}
else {
tmp[k++] = nums[j++];
}
}
while (i <= mid) {
tmp[k++] = nums[i++];
}
while (j <= high) {
tmp[k++] = nums[j++];
}
for (k = low; k <= high; ++k) {
nums[k] = tmp[k];
}
}
int main()
{
vector<int> nums({ 0,4,6,63,55,54,75,18,9,6 });
vector<int> tmp(nums.size()); //辅助数组
mergesort(nums, 0, nums.size() - 1,tmp);
for (auto& x : nums) {
cout << x << ' ';
}
}
基于单链表的归并排序:
解析参考:https://leetcode-cn.com/problems/sort-list/solution/sort-list-gui-bing-pai-xu-lian-biao-by-jyd/
https://leetcode-cn.com/problems/sort-list/solution/148-pai-xu-lian-biao-jiu-yin-wei-zhe-ge-ti-bei-wu-/
与上面链接中实现略有不同的是此处所有链表操作都带有伪头节点。
//基于单链表的归并排序(单链表都含伪头节点)
linkList* merge(linkList* l1, linkList* l2) {//排序合并两个链表,返回值为linkList*
linkList* h = new linkList(0);
linkList* res = h;
linkList* left = l1->next, * right = l2->next;
while (left != NULL && right != NULL) {
if (left->val < right->val) {
h->next = left;
left = left->next;
}
else {
h->next = right;
right = right->next;
}
h = h->next;
}
h->next = left != NULL ? left : right; //连接剩下的链表元素
return res;
}
//递归 分割单链表至每个链表只含一个节点,然后合并(排序)
linkList* mergesort(linkList* head) { //cut
//cut 递归终止条件
if (head->next == NULL || head->next->next == NULL) {
return head;
}
//使用快慢指针找到链表中点,断开
linkList* fast = head->next->next, *slow = head->next;
while (fast != NULL && fast->next != NULL) {
slow = slow->next;
fast = fast->next->next;
}
linkList* tmp = new linkList(0);//断开后第二个链表的伪头节点
tmp->next = slow->next;
slow->next = NULL; //断开
//递归分割
linkList* left = mergesort(head);
linkList* right = mergesort(tmp);
//逐层合并
return merge(left, right);
}
int main()
{
linkList* head = creatlist();
linkList* res = mergesort(head); //此返回值为最后一次调用的merge返回的指针
linkList* p = res->next;
while (p != NULL) {
cout << p->val << ' ';
p = p->next;
}
cout << endl;
}
上述实现归并排序的方式是用递归的方式将链表逐层分割为单个节点,再层层合并,空间复杂度为O(logn)。若要求空间复杂度为O(1),则可采用非递归的归并排序,用迭代的方式分割链表并合并,第一次分割为单个节点,合并,这样使每两个节点有序;第二次分割每两个为一个链表,合并…;直至整个链表有序。:
//cut n个节点,然后返回剩下的链表的头节点
linkList* cut(linkList* head,int n) {
linkList* p = head;
while (--n && p != NULL) {
p = p->next;
}
if (p == NULL) {
return NULL;
}
linkList* suc = p->next; //剩下链表的头节点
p->next = NULL; //断开链表
return suc;
}
//待合并的两个链表不含伪头节点
linkList* merge(linkList* left, linkList* right) {
linkList* h = new linkList(0);
linkList* res = h;
while (left != NULL && right != NULL) {
if (left->val < right->val) {
h->next = left;
left = left->next;
}
else {
h->next = right;
right = right->next;
}
h = h->next;
}
h->next = left != NULL ? left : right; //连接剩下的链表元素
return res->next;
}
linkList* mergesort(linkList* head) { //cut
if (head->next == NULL || head->next->next == NULL) {
return head;
}
int length = 0;
linkList* p = head->next;
while (p != NULL) {
length++;
p = p->next;
}
//第一次cut 1,然后根据归并的思路,cut的大小依次*2,边界条件位size
//因为size==n表示的是链表的每个长度为n的段已经是有序的了,
//执行循环的目的就是把有序的长度为n的段连起来,因此当size>=length时,表示长度为size的段已经有序,
//即原链表已经归并完成,结束循环。只有当size
for (int size = 1; size < length; size *= 2) {
//cur表示待分割链表的第一个,tail表示已经合并好的链表的最后一个
linkList* cur = head->next;
linkList* tail = head;
while (cur!=NULL) {
linkList* left = cur;
linkList* right = cut(left, size);//使left被cut为size,且返回剩下的元素链表
cur = cut(right, size); //right被cut为size长度,返回剩下链表
tail->next = merge(left, right); //将前一个合并的链表与后面合并的链表相连
while (tail->next) { //使tail指向当前连起来的链表的尾部
tail = tail->next;
}
}
}
return head->next;
}
int main()
{
linkList* head = creatlist();
head = mergesort(head);
linkList* p = head->next;
while (p != NULL) {
cout << p->val << ' ';
p = p->next;
}
cout << endl;
}
五、基数排序
9.基数排序 Radix sort
也称**桶排序 bucket sort **。不基于比较,借助多关键字排序的思想对单逻辑关键字进行排序。
稳定!
时间复杂度:O(d*(n+r)) d为元素关键字个数,r为基数,n为元素个数。进行d趟分配和收集每趟分配n次,收集r次(r相当于桶的个数)。
空间复杂度:O ( r ) 需要r个队列。
MSD法(Most Significant Digit first):最搞位优先法
LSD法(Least Significant Digit first):最低位优先法
桶排序实例: https://leetcode-cn.com/problems/sort-characters-by-frequency/submissions/
https://leetcode-cn.com/problems/top-k-frequent-elements/
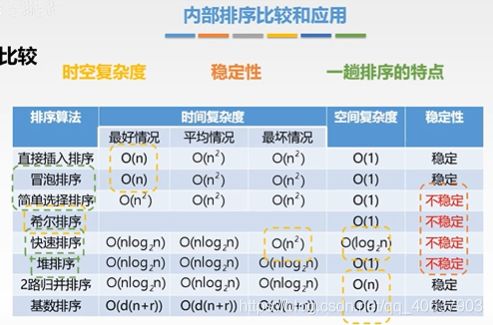
| 直接插入排序 | 顺序+链式 |
|---|---|
| 折半插入排序 | 顺序 |
| 希尔排序 | 顺序 |
| 冒泡排序 | 顺序+链式 |
| 快速排序 | 顺序+链式 |
| 选择排序 | 顺序+链式 |
| 堆排序 | 顺序+链式 |
| 基数排序 | 顺序+链式 |