第四章 分治策略 4.6 证明主定理

4.6 证明主定理

一.

1.

  当我们在一个局限的值域上使用渐近符号时，必须要时刻小心，避免得到错误的结论。例如：对 $n$ 是 $2$ 的幂的情况证明 $T(n)=O(n)$ 并不保证 $T(n)=O(n)$ 。函数 $T(n)$ 可能是这样定义的：
$$T(n)=\{\begin{array}{ll}n& \text{若 n=1,2,4,8,...}\\ n^2& \text{其他}\end{array}$$
  此例中适用于所有 $n$ 值的最佳上界为 $T(n)=O(n^2)$ 。由于可能导致这种严重后果，在并不绝对清楚应用环境的情况下，永远也不要在一个有限的值域上使用渐近符号。

2. 对 $b$ 的幂证明主定理

  主定理第一部分分析主定理的递归式 $（4.20）$ ：
$$T(n)=aT(\frac{n}{b})+f(n)$$
  假定 $n$ 是 $b(b>1)$ 的幂， $b$ 不一定是一个整数。

  引理 $4.2$ ：

  令 $a\ge 1$ 和 $b>1$ 是常数， $f(n)$ 是一个定义在 $b$ 的幂上的非负函数。 $T(n)$ 是定义在 $b$ 的幂上的递归式：
$$T(n)=\{\begin{array}{ll}\Theta (1)& \text{若 n=1}\\ aT(\frac{n}{b})+f(n)& \text{若 n=bi}\end{array}$$
  其中 $i$ 是正整数。那么$$T(n)=\Theta (n^{{\log }_{b}a})+\sum _{j=0}^{{\log }_{b}n-1}{a}^{j}f(\frac{n}{b^j})$$

  证明：

  使用如图 $4-7$ 中的递归树。树的根结点的代价为 $f(n)$ ，它有 $a$ 个孩子结点，每个的代价为 $f(b/n)$ 。（将 $a$ 看做一个整数非常方便，当可视化递归树时尤其如此，但从数学角度并不要求这一点）。每个孩子结点又有 $a$ 个孩子，使得在深度为 $2$ 的层次上有 $a^2$ 个结点，每个的代价为 $f(n/b^2)$ 。一般地，深度为 $j$ 的层次上有 $a^j$ 个结点，每个的代价为 $f(n/b^j)$ 。每个叶结点的代价为 $T(1)=\Theta (1)$ ，深度为 ${\log }_{b}n$ ，因为 $n/b^{{\log }_{b}n}=1$ 。树中共有 $a^{{\log }_{b}n}=n^{{\log }_{b}a}$ 个叶结点。

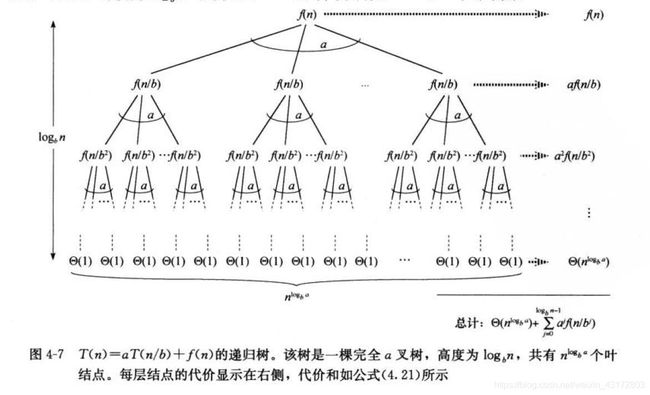
  我们将图 $4-7$ 所示的递归树中的每层节点的代价求和，得到公式 $（4.21）$ 。深度为 $j$ 的所有内部结点的代价为 $a^{j}f(n/b^j)$ ，所以内部结点的总代价为：$$\sum _{j=0}^{{\log }_{b}n-1}{a}^{j}f(\frac{n}{b^j})$$
  在分治算法中，这个和表示分解子问题与合并子问题的代价。所有叶结点的代价（表示完成所有 $n^{{\log }_{b}a}$ 个规模为 $1$ 的子问题的代价）为 $\Theta (n^{{\log }_{b}a})$ 。

  从递归树看，主定理的三种情况分别对应以下三种情况：（1）树的总代价有叶结点的代价决定；（2）树的总代价均匀分布在树的所有层次上；（3）树的总代价由根结点的代价决定。

  引理4.3

  令 $a\ge 1$ 和 $b>1$ 是常数， $f(n)$ 是一个定义在 $b$ 的幂上的非负函数。 $g(n)$ 是定义在 $b$ 的幂上的函数：
$$g(n)=\sum _{j=0}^{{\log }_{b}n-1}{a}^{j}f(\frac{n}{b^j})(4.22)$$
  对 $b$ 的幂， $g(n)$ 有如下渐近界：
  1. 若对某个常数 $ϵ>0$ 有 $f(n)=O(n^{{\log }_{b}a-ϵ})$ ， $g(n)=O(n^{{\log }_{b}a})$ 。
  2. 若 $f(n)=\Theta (n^{{\log }_{b}a})$ ，则 $g(n)=O({\log }_{b}a\lg n)$ 。
  3. 若对某个常数 $c<1$ 和所有足够大的 $n$ 有 $af(n/b)\le cf(n)$ ，则 $g(n)=\Theta (f(n))$ 。

  证明：

对情况 $1$ ，我们有 $f(n)=O(n^{{\log }_{b}a-ϵ})$ ，这意味着 $f(n/b^j)=O((n/b^j{)}^{{\log }_{b}a-ϵ})$ 。代入公式 $（4.22）$ 得$$g(n)=O(\sum _{j=0}^{{\log }_{b}n-1}{a}^j(\frac{n}{b^j}{)}^{{\log }_{b}a-ϵ})(4.23)$$  对于 $O$ 符号内的和式，通过提取因子并化简来求它的界，得到一个递增的几何级数：$$\begin{array}{rl}\sum _{j=0}^{{\log }_{b}n-1}{a}^j(\frac{n}{b^j}{)}^{{\log }_{b}a-ϵ}& =n^{{\log }_{b}a-ϵ}\sum _{j=0}^{{\log }_{b}n-1}(\frac{a{b}^{ϵ}}{b^{{\log }_{b}a}}{)}^j\\ & =n^{{\log }_{b}a-ϵ}\sum _{j=0}^{{\log }_{b}n-1}(b^{ϵ}{)}^j\\ & =n^{{\log }_{b}a-ϵ}(\frac{b^{ϵ{\log }_{b}n}-1}{b^{ϵ}-1})\\ & =n^{{\log }_{b}a-ϵ}(\frac{n^{ϵ}-1}{b^{ϵ}-1})\end{array}$$
  由于 $b$ 和 $ϵ$ 是常数，因此可以将最后一个表达式重写为 $n^{{\log }_{b}a-ϵ}O(n^{ϵ})=O(n^{{\log }_{b}a})$ 。用表达式代换公式 $(4.23)$ 中的和式，得到 $g(n)=O({\log }_{b}a)$ ，因此情况 $1$ 得证。
  由于情况 $2$ 假定 $f(n)=\Theta (n^{{\log }_{b}a})$ ，因此有 $f(n/b^j)=\Theta ((n/b^j{)}^{{\log }_{b}a})$ 。代入公式 $(4.22)$ 得
$$g(n)=\Theta (\sum _{j=0}^{{\log }_{b}n-1}{a}^j(\frac{n}{b^j}{)}^{{\log }_{b}a})(4.24)$$
  采用于情况 $1$ 相同的方式，求出 $\Theta$ 符号内和式的界，但这次并未得到一个几何级数，而是发现和式的每一项都是相同的：
$$\sum _{j=0}^{{\log }_{b}n-1}{a}^j(\frac{n}{b^j}{)}^{{\log }_{b}a}=n^{{\log }_{b}a}\sum _{j=0}^{{\log }_{b}n-1}(\frac{a}{b^{{\log }_{b}a}}{)}^j=n^{{\log }_{b}a}\sum _{j=0}^{{\log }_{b}n-1}1=n^{{\log }_{b}a}{\log }_{b}n$$
  用这个表达式替换公式 $(4.24)$ 中的和式，我们得到
$$g(n)=\Theta (n^{{\log }_{b}a}{\log }_{b}n)=\Theta (n^{{\log }_{b}a}\lg n)$$
  情况 $2$ 得证。
  情况 $3$ 的证明类似。由于 $f(n)$ 出现在 $g(n)$ 的定义 $(4.22)$ 中，且 $g(n)$ 的所有项都是非负的，因此可以得出结论：对 $b$ 的幂， $g(n)=\Omega (f(n))$ 。假定在这个引理中，对某个常数为 $c<1$ 和所有足够大的 $n$ 有 $af(n/b)\le cf(n)$ 。将这个假设改写为 $f(n/b)\le (c/a)f(n)$ 并迭代 $j$ 次，得到 $f(n/b^j)\le (c/a{)}^{j}f(n)$ ，或等价地， $a^{j}f(n/b^j)\le c^{j}f(n)$ ，其中假设进行迭代的值足够大。由于最后一个，也就是最小的值 $n/b^{j-1}$ ，因此假定 $n/b^{j-1}$ 足够大就够了。
  代入公式 $(4.22)$ 并化简，我们得到一个几何级数，但与情况 $1$ 证明中的几何级数不同，这次得到的是递减的几何级数。使用一个 $O(1)$ 项来表示 $n$ 足够大这个假设未覆盖的项。
$$\begin{array}{rlr}g(n)& =\sum _{j=0}^{{\log }_{b}n-1}{a}^{j}f(n/b^j)& \\ & \le \sum _{j=0}^{{\log }_{b}n-1}{c}^{j}f(n)+O(1)& \\ & \le f(n)\sum _{j=0}^{\infty }{c}^j+O(1)& \\ & =f(n)(\frac{1}{1-c})+O(1)& \\ & =O(f(n))& \end{array}$$  因为 $c$ 是一个常数。因此可以得到结论：对 $b$ 的幂， $g(n)=\Theta (f(n))$ 。情况 $3$ 得证，引理证毕。

  引理4.4

  令 $a\ge 1$ 和 $b>1$ 是常数， $f(n)$ 是一个定义在 $b$ 的幂上的非负函数。 $T(n)$ 是定义在 $b$ 的幂上的递归式：
$$T(n)=\{\begin{array}{ll}\Theta (1)& \text{若 n=1}\\ aT(n/b)+f(n)& \text{若n=bi}\end{array}$$
  其中 $i$ 是正整数。那么对 $b$ 的幂， $T(n)$ 有如下渐近界：
  1. 若对某个常数 $ϵ>0$ 有 $f(n)=O(n^{{\log }_{b}a-ϵ})$ ，则 $T(n)=\Theta (n^{{\log }_{b}a})$ 。
  2. 若 $f(n)=\Theta (n^{{\log }_{b}a})$ ，则 $T(n)=\Theta (n^{{\log }_{b}a}\lg n)$ 。
  3. 若对某个常数 $ϵ>0$ ，有 $f(n)=\Omega (n^{{\log }_{b}a+ϵ})$ ，并且对某个常数 $c<1$ 和足够大的 $n$ ，有 $af(n/b)\le cf(n)$ ，则 $T(n)=\Theta (f(n))$ 。

  证明：

  利用引理 $4.3$ 中的界对引理 $4.2$ 中的和式 $（4.21）$ 进行求值。对情况 $1$ ，我们有
$$T(n)=\Theta (n^{{\log }_{b}a})+O(n^{{\log }_{b}a})=\Theta (n^{{\log }_{b}a})$$
  对于情况 $2$ ，
$$T(n)=\Theta (n^{{\log }_{b}a})+\Theta (n^{{\log }_{b}a}\lg n)=\Theta (n^{{\log }_{b}a}\lg n)$$
  对于情况 $3$ ，
$$T(n)=\Theta (n^{{\log }_{b}a})+\Theta (f(n))=\Theta (f(n))$$
  因为 $f(n)=\Omega (n^{{\log }_{b}a+ϵ})$ 。

3. 向下取整和向上取整

$$T(n)=aT(\lceil n/b\rceil )+f(n)(4.25)$$$$T(n)=aT(\lfloor n/b\rfloor )+f(n)(4.26)$$
  对第一种情况应用下界 $\lceil n/b\rceil \ge n/b$ 来得到所需结果，对第二种情况应用上界 $\lfloor n/b\rfloor \le n/b$ 。可以使用几乎一样的技术来处理递归式 $（4.26）$ 的下界和递归式的 $（4.25）$ 的上界，因此我们给出后一个界的证明。
  对图 $4-7$ 的递归树进行修改，得到图 $4-8$ 中的递归树。当沿着递归树向下时，我们得到如下递归调用的参数序列：
n ⌈ n / b ⌉ ⌈ ⌈ n / b ⌉ / b ⌉ ⌈ ⌈ ⌈ n / b ⌉ / b ⌉ / b ⌉ . . . \begin{aligned}&n\\&\lceil n/b\rceil\\&\lceil\lceil n/b\rceil /b\rceil\\&\lceil\lceil\lceil n/b\rceil/b\rceil/b\rceil\\&...\end{aligned} ​n⌈n/b⌉⌈⌈n/b⌉/b⌉⌈⌈⌈n/b⌉/b⌉/b⌉...​
  用 $n_j$ 表示序列中第 $j$ 个元素，其中
$$n_j=\{\begin{array}{ll}n& \text{若 j=0}\\ \lceil n_{j-1}/n\rceil & \text{若 j>0}\end{array}$$
  我们的第一个目标是确定 $n_k$ 是常数时的深度 $k$ 。利用不等式 $\lceil x\rceil \le x+1$ ，可得
$$\begin{array}{rl}& n_0\le n\\ & n_1\le \frac{n}{b}+1\\ & n_2\le \frac{n}{b^2}+\frac{1}{b}+1\\ & n_3\le \frac{n}{b^3}+\frac{1}{b^2}+\frac{1}{b}+1\\ & ...\end{array}$$
  一般地，我们有
$$n_j\le \frac{n}{b^j}+\sum _{i=0}^{j-1}\frac{1}{b^i}<\frac{n}{b^j}+\sum _{i=0}^{\infty }\frac{1}{b^i}=\frac{n}{b^j}+\frac{b}{b-1}$$
  令 $j=\lfloor {\log }_{b}n\rfloor$ ，可得
$$\begin{array}{rl}{n}_{\lfloor {\log }_{b}n\rfloor }& <\frac{n}{b^{\lfloor {\log }_{b}n\rfloor }}+\frac{b}{b-1}<\frac{n}{b^{{\log }_{b}n-1}}+\frac{b}{b-1}=\frac{n}{n/b}+\frac{b}{b-1}\\ & =b+\frac{b}{b-1}=O(1)\end{array}$$
  因此我们可以看到在深度 $\lfloor {\log }_{b}n\rfloor$ ，问题规模至多是常数。

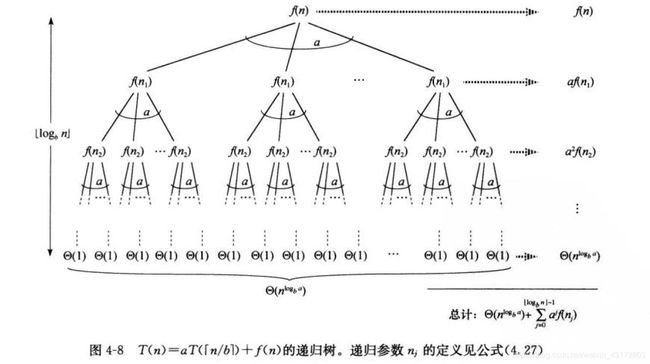
  从图 $4-8$ 可以看出，
$$T(n)=\Theta (n^{{\log }_{b}a})+\sum _{j=0}^{\lfloor {\log }_{b}n\rfloor -1}{a}^{j}f(n_j)(4.28)$$
  对和式求值：
$$g(n)=\sum _{j=0}^{\rfloor {\log }_{b}n\rfloor -1}{a}^{j}f(n_j)$$
  方法与引理 $4.3$ 的证明类似。我们从情况 $3$ 开始，如果对 $n>b+b/(b-1)$ ， $af(\lfloor n/b\rfloor )\le cf(n)$ 成立，其中 $c<1$ 是常数，则有 $a^{j}f(n_j)\le c^{j}f(n)$ 。因此，我们可以像引理 $4.3$ 的证明一样来对公式 $（4.29）$ 的和式进行求值。对于情况 $2$ ，我们有 $f(n)=\Theta (n^{{\log }_{b}a})$ 。如果能证明 $f(n_j)=O(n^{{\log }_{b}a}/a^j)=O((n/b^j{)}^{{\log }_{b}a})$ ，则情况 $2$ 的证明直接使用引理 $4.3$ 证明的方法即可。观察到 $j\le \lfloor {\log }_{b}n\rfloor$ 意味着 $b^j/n\le 1$ 。界 $f(n)=O({\log }_{b}a)$ 意味着存在常数 $c>0$ ，使得对所有足够大的 $n_j$ ，
$$\begin{array}{rl}f(n_j)& \le c(\frac{n}{b^j}+\frac{b}{b-1}{)}^{{\log }_{b}a}=c(\frac{n}{b^j}(1+\frac{b^j}{n}\cdot \frac{b}{b-1}){)}^{{\log }_{b}a}\\ & =c(\frac{n^{{\log }_{b}a}}{a^j})(1+(\frac{b^j}{n}\cdot \frac{b}{b-1}){)}^{{\log }_{b}a}\\ & \le c(\frac{n^{{\log }_{b}a}}{a^j})(1+\frac{b}{b-1}{)}^{{\log }_{b}a}=O(\frac{n^{{\log }_{b}a}}{a^j})\end{array}$$
  因为 $c(1+b/(b-1){)}^{{\log }_{b}a}$ 是常量。因此，情况 $2$ 得证，情况 $1$ 的证明几乎是一样的。关键是证明界 $f(n_j)=O((n/b^j{)}^{{\log }_{b}a-ϵ})$ ，这部分与情况 $2$ 证明中的对应部分相似，尽管使用的代数方法更复杂些。
  现在我们已经对所有整数 $n$ 证明了主定理的上界，下界的证明类似。

二. 维基百科上的master定理

1. 一般形式

   The master theorem often yields asymptotically tight bounds to some recurrences from divide and conquer algorithms that partition an input into smaller subproblems of equal sizes, solve the subproblems recursively, and then combine the subproblem solutions to give a solution to the original problem. The time for such an algorithm can be expressed by adding the work that they perform at the top level of their recursion (to divide the problems into subproblems and then combine the subproblem solutions) together with the time made in the recursive calls of the algorithm. If $T(n)$ denotes the total time for the algorithm on an input of size $n$, and $f(n)$ denotes the amount of time taken at the top level of the recurrence then the time can be expressed by a recurrence relation that takes the form:
$$T(n)=aT\left(\frac{n}{b}\right)+f(n)$$
   Here $n$ is the size of an input problem, $a$ is the number of subproblems in the recursion, and $b$ is the factor by which the subproblem size is reduced in each recursive call. The theorem below also assumes that, as a base case for the recurrence, $T(n)=\Theta (1)$ when $n$ is less than some bound $\kappa >0$, the smallest input size that will lead to a recursive call.
   Recurrences of this form often satisfy one of the three following regimes, based on how the work to split/recombine the problem $f(n)$ relates to the critical exponent $c_{\mathrm{crit}}={\log }_{b}a$. (The table below uses standard big O notation.)


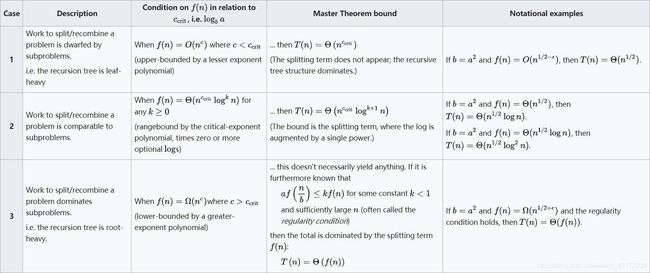
A useful extension of Case 2 handles all values of $k$:

三.

*4.6-1

  对 $b$ 是正整数而非任意实数的情况，给出公式 $（4.27）$ 中 $n_j$ 的简单而准确的表达式。

  解：$$n_j=\lceil \frac{n}{b^j}\rceil$$    对任意正整数 $a$ 和 $b$ ，任意实数 $x$ ，有$$\lceil \frac{x}{a}\rceil -1<\frac{x}{a}\le \lceil \frac{x}{a}\rceil$$$$\frac{1}{b}(\lceil \frac{x}{a}\rceil -1)<\frac{x}{ab}\le \frac{1}{b}\lceil \frac{x}{a}\rceil$$    显然 $P=\lceil x/a\rceil$ 是整数，令 $P=q\cdot b-r$ ，其中 $0<r\le b$ ，且 $P>(q-1)b$ ，从而 $P-1\ge (q-1)b$ 。因此有$$q-1\le \frac{P-1}{b}<\frac{x}{ab}\le \frac{P}{b}\le q$$    即 $$\lceil \frac{x}{ab}\rceil =\lceil \frac{1}{b}\lceil \frac{x}{a}\rceil \rceil$$    故 $$n_j=\lceil \frac{n_{j-1}}{b}\rceil =\lceil \frac{1}{b}\lceil \frac{n}{b^{j-1}}\rceil \rceil =\frac{n}{b^j}$$    然而对任意实数 $P>(q-1)b$ 是推不出 $P-1\ge (q-1)b$ 。

*4.6-2

  证明：如果 $f(n)=\Theta (n^{{\log }_{b}a}{\lg }^{k}n)$ ，其中 $k\ge 0$ ，那么主递归式的解为 $T(n)=\Theta (n^{{\log }_{b}a}{\lg }^{k+1}n)$ 。为简单起见，假定 $n$ 是 $b$ 的幂。

  证明：首先设$$g(n)=\sum _{j=0}^{{\log }_{b}n-1}{a}^{j}f(\frac{n}{b^j})$$       因此$$f(\frac{n}{b^j})=\Theta ((\frac{n}{b^j}{)}^{{\log }_{b}a}{\lg }^k(\frac{n}{b^j}))$$       于是$$g(n)=\Theta (\sum _{j=0}^{{\log }_{b}n-1}{a}^j(\frac{n}{b^j}{)}^{{\log }_{b}a}{\lg }^k(\frac{n}{b^j}))$$      从而有$$\begin{array}{rl}\sum _{j=0}^{{\log }_{b}n-1}{a}^j(\frac{n}{b^j}{)}^{{\log }_{b}a}{\lg }^k\frac{n}{b^j}& =n^{{\log }_{b}a}\sum _{j=0}^{{\log }_{b}n-1}(\frac{a}{b^{{\log }_{b}a}}{)}^j{\lg }^k\frac{n}{b^j}\\ & =n^{{\log }_{b}a}\sum _{j=0}^{{\log }_{b}n-1}{\lg }^k\frac{n}{b^j}\end{array}$$      而$$l{g}^k\frac{n}{d}=(\lg n-\lg d{)}^k={\lg }^{k}n+o({\lg }^{k}n)$$      于是$$\begin{array}{rl}\sum _{j=0}^{{\log }_{b}n-1}{\lg }^k\frac{n}{b^j}& =\sum _{j=0}^{{\log }_{b}n-1}({\lg }^{k}n+o({\lg }^{k}n))\\ & ={\log }_{b}n{\lg }^{k}n+{\log }_{b}n\cdot o({\lg }^{k}n)\\ & =\Theta ({\log }_{b}n{\lg }^{k}n)\\ & =\Theta ({\lg }^{k+1}n)\end{array}$$      从而$$T(n)=\Theta (n^{{\log }_{b}a}{\lg }^{k+1}n)$$

*4.6-3

  证明：主定理中的情况 $3$ 被过分强调了，从某种意义上来说，对某个常数 $c<1$ ，正则条件 $af(n/b)\ge cf(n)$ 成立本身就意味着存在常数 $ϵ>0$ ，使得 $f(n)=\Omega (n^{{\log }_{b}a+ϵ})$ 。

  证明：对于式子$$af(n/b)\le cf(n)$$      令 $\alpha =a/c$ ，则$$\alpha f(n/b)\le f(n)$$      即$$\alpha f(n)\le f(n/b)$$      令 $n=b^i$ ，不断迭代$${\alpha }^{i}f(1)\le f(b^i)$$      而$$i={\log }_{b}n$$      于是$$f(n)\ge {\alpha }^{{\log }_{b}n}f(1)=n^{{\log }_b\alpha }$$      由于 $c<1$ ，于是$$\alpha >a$$      令$$\alpha =a+d,d>0$$      故而 $$f(n)={\log }_{b}a+{\log }_{b}d=n^{{\log }_{b}a+ϵ}$$      其中 $$ϵ={\log }_{b}d$$

四.

4-1 （递归式例子）

  对下列每个递归式，给出 $T(n)$ 的渐近上界和渐近下界。假定 $n\le 2$ 时 $T(n)$ 是常数。给出尽量紧确的界，并验证其正确性。

  a. $T(n)=2T(n/2)+n^4$
  b. $T(n)=T(7n/10)+n$
  c. $T(n)=16T(n/4)+n^2$
  d. $T(n)=7T(n/3)+n^2$
  e. $T(n)=7T(n/2)+n^2$
  f. $T(n)=2T(n/2)+\sqrt{n}$
  g. $T(n)=T(n-1)+n^2$

  解：
    a. $\Theta (n^4)$
    b. $\Theta (n)$
    c. $\Theta (n^2\lg n)$
    d. $\Theta (n^2)$
    e. $\Theta (n^{\lg 7})$
    f. $\Theta (\sqrt{n}\lg n)$
    g. $\Theta (n^3)$

4-2 （参数传递代价）

  我们有一个贯穿本书的假设——过程调用中的参数传递花费常量时间，即使传递一个 $N$ 个元素的数组也是如此。在大多数系统中，这个假设是成立的，因为传递的是指向数组的指针，而非数组本身。本体讨论三种参数传递策略：

  1. 数组通过指针来传递。时间 $=\Theta (1)$ 。
  2. 数组通过元素复制来传递。时间 $=\Theta (N)$ ，其中 $N$ 是数组的规模。
  3. 传递数组时，只复制过程可能访问的子区域。若子数组 $A[p..q]$ 被传递，则时间 $=\Theta (p-q+1)$ 。

  a. 考虑在有序数组中查找元素的递归二分查找算法（参见练习 2. 3-5）。分别给出上述三种参数传递策略下，二分查找最坏情况运行时间的递归式，并给出递归式解的好的上界。
   令 $N$ 为原问题的规模， $n$ 为子问题的规模。
  b. 对 2.3.1 节的 MERGE-SORT 算法重做 (a) 。

  解.a. 1. $T(n)=T(n/2)+c=\Theta (\lg n)$
     2. $T(n)=T(n/2)+cN=\Theta (n\lg n)$
     3. $T(n)=T(n/2)+cn=\Theta (n)$
    b. 1. $T(n)=2T(n/2)+cn=\Theta (n\lg n)$
     2. $T(n)=2T(n/2)+cn+2N=\Theta (n^2)$
     3. $T(n)=2T(n/2)+cn+2n/2=\Theta (n\lg n)$

4-3 （更多的递归式例子）

  对下列每个递归式，给出 $T(n)$ 的渐近上界和下界。假定对足够小的 $n$ ， $T(n)$ 是常数。给出尽量紧确的界，并验证其正确性。

  a. $T(n)=4T(n/3)+n\lg n$
  b. $T(n)=3T(n/3)+n/\lg n$
  c. $T(n)=4T(n/2)+n^2\sqrt{n}$
  d. $T(n)=3T(n/3-2)+n/2$
  e. $T(n)=2T(n/2)+n/\lg n$
  f. $T(n)=T(n/2)+T(n/4)+T(n/8)+n$
  g. $T(n)=T(n-1)+1/n$
  h. $T(n)=T(n-1)+\lg n$
  i. $T(n)=T(n-2)+1/\lg n$
  j. $T(n)=\sqrt{n}T(\sqrt{n})+n$

  解：a. $\Theta (n^{{\log }_{3}4})$
    b. $\Theta (n\lg \lg n)$ ，证明如下：$$\begin{array}{rl}T(n)& =3T(n/3)+\frac{3}{\lg n}\\ & =n\Theta (1)+\sum _{i=0}^{{\log }_{3}n-1}\frac{n}{\lg n-i}\\ & =n\Theta (1)+n\sum _{i=1+\lg n-{\log }_{3}n}^{\lg n}\frac{1}{i}\\ & =\Theta (n\lg \lg n)\end{array}$$

    c. $\Theta (n^2\sqrt{n})$
    d. $\Theta (n\lg n)$
    e. $\Theta (n\lg \lg n)$，证明同b.
    f. $\Theta (n)$ ，证明如下：
     当 $k<n$ 时，$T(k)\le ck$，则：$$\begin{array}{rlr}T(n)& =T(n/2)+T(n/4)+T(n/8)+n& \\ & \le cn/2+cn/4+cn/8+n& \\ & \le 7cn/8+n& \\ & \le cn& \text{当 c≥8 时成立}\end{array}$$     当 $k<n$ 时，$T(k)\ge k$，则：$$\begin{array}{rl}T(n)& =T(n/2)+T(n/4)+T(n/8)+n\\ & \ge n/2+n/4+n/8+n\\ & \ge n\end{array}$$

    g. 由 $Eular$ 常数：$$\underset{n\to \infty }{\lim }(1+\frac{1}{2}+...+\frac{1}{n}-\ln n)=C$$      可知复杂度为 $\Theta (\lg n)$
    h. $\Theta (n\lg n)$，证明如下：$$\begin{array}{rl}T(n)& =T(n-1)+\lg n=\sum _{i=0}^{n-1}\lg (n-i)=\sum _{i=1}^n\lg i\\ & =\Theta (\lg (n!))=\Theta (n\lg n)\end{array}$$

    i. $\Theta (\lg \lg n)$，证明如下：$$\begin{array}{rl}T(n)& =T(n-2)+\frac{1}{\lg n}=\frac{1}{\lg n}+...+\Theta (1)\\ & =\sum _{i=0}^{n/2-1}\frac{1}{\lg (n-2i)}=\sum _{i=2}^n\frac{1}{\lg i}\\ & =\sum _{i=1}^{\lg n}\frac{1}{i}\\ & =\Theta (\lg \lg n)\end{array}$$

    j. $\Theta (n\lg \lg n)$，证明如下：
     令 $S(n)=T(n)/n$ ，则 $S(n)=S(\sqrt{n})+1$ ，当 $n=2^m$ ，有 $S(2^m)=S(2^{m/2})+1$ 。令 $P(m)=S(2^m)$ ，得 $P(m)=P(m/2)+1$ 。于是 $P(m)=\Theta (\lg m)$ 。则 $T(n)=\Theta (n\lg \lg n)$ 。

4-4 （斐波那契数）

  本题讨论递归式（3.22）定义的斐波那契数的性质。我们将使用生成函数技术来求斐波那契递归式。生成函数（又称为形式幂级数）$\mathcal{F}$ 定义为$$\mathcal{F}(z)=\sum _{i=0}^{\infty }{F}_i{z}^i=0+z+z^2+2z^3+3z^4+5z^5+8z^6+13z^7+21z^8+...$$
  其中 $F_i$ 为第 $i$ 个斐波那契数。

  a. 证明：$\mathcal{F}(z)=z+z\mathcal{F}(z)+z^2\mathcal{F}(z)$ 。
  b. 证明：$$\mathcal{F}(z)=\frac{z}{1-z-z^2}=\frac{z}{(1-\varphi z)(1-\hat{\varphi }z)}=\frac{1}{\sqrt{5}}(\frac{1}{1-\varphi z}-\frac{1}{1-\hat{\varphi }z})$$
   其中$$\begin{array}{rl}\varphi & =\frac{1+\sqrt{5}}{2}=1.61803...\\ \hat{\varphi }& =\frac{1-\sqrt{5}}{2}=-0.61803...\end{array}$$
  c. 证明：$$\mathcal{F}(z)=\sum _{i=0}^{\infty }\frac{1}{\sqrt{5}}({\varphi }^i-{\hat{\varphi }}^i)z^i$$
  d. 证明：利用 （c） 的结果证明：对 $i>0$ ， $F_i={\varphi }^i/\sqrt{5}$ ，结果舍入到最接近的整数。（提示：观察到 $|\hat{\varphi }|<1$ 。）

  证明：a. $$\begin{array}{rl}z+\mathcal{F}(z)+z^2\mathcal{F}(z)& =z+z\sum _{i=0}^{\infty }{F}_i{z}^i+z^2\sum _{i=0}^{\infty }{F}_i{z}^i\\ & =z+\sum _{i=1}^{\infty }{F}_{i-1}{z}^i+\sum _{i=2}^{\infty }{F}_{i-2}{z}^i\\ & =z+F_{1}z+\sum _{i=2}^{\infty }(F_{i-1}+F_{i-2})z^i\\ & =z+F_{1}z+\sum _{i=2}^{\infty }{F}_i{z}^i\\ & =\mathcal{F}(z)\end{array}$$

     b. $$\begin{array}{rl}\mathcal{F}(z)& =\frac{\mathcal{F}(z)(1-z-z^2)}{1-z-z^2}\\ & =\frac{\mathcal{F}(z)-z\mathcal{F}(z)-z^2\mathcal{F}(z)-z+z}{1-z-z^2}\\ & =\frac{\mathcal{F}(z)-\mathcal{F}(z)+z}{1-z-z^2}\\ & =\frac{z}{1-z-z^2}\\ & =\frac{z}{1-(\varphi +\hat{\varphi })z-z^2}\\ & =\frac{z}{(1-\varphi z)(1-\hat{\varphi }z)}\\ & =\frac{z(\frac{1}{1-\varphi z}-\frac{1}{1-\hat{\varphi }z})}{\sqrt{5}z}\\ & =\frac{1}{\sqrt{5}}(\frac{1}{1-\varphi z}-\frac{1}{1-\hat{\varphi }z})\end{array}$$

     c. 由于 $$\frac{1}{1-x}=\sum _{k=0}^{\infty }{x}^k\text{当|x|<1时}$$

      于是 $$\begin{array}{rl}\mathcal{F}(z)& =\frac{1}{\sqrt{5}}(\frac{1}{1-\varphi z}-\frac{1}{1-\hat{\varphi }z})\\ & =\frac{1}{\sqrt{5}}(\sum _{i=0}^{\infty }{\varphi }^i{z}^i-\sum _{i=0}^{\infty }{\hat{\varphi }}^i{z}^i)\\ & =\sum _{i=0}^{\infty }\frac{1}{\sqrt{5}}({\varphi }^i-{\hat{\varphi }}^i)z^i\end{array}$$

     d. 显然$$\begin{array}{r}{F}_i=\frac{1}{\sqrt{5}}({\varphi }^i-{\hat{\varphi }}^i)\end{array}$$

      于是 $0<|{\hat{\varphi }}^i|<1$
      故而$$F_i\approx \frac{{\varphi }^i}{\sqrt{5}}$$

4-5 （芯片检测）

   Diogenes 教授有 $n$ 片可能完全一样的集成电路芯片，原理上可以用来相互检测。教授的测试夹具同时只能容纳两块芯片。当夹具装载上时，每块芯片都检测另一块，并报告它是好是坏。一块好的芯片总能准确报告另一块芯片的好坏，但教授不能信任坏芯片报告的结果。因此，4 种可能的测试结果如下：

芯片 $A$ 的结果	芯片 $B$ 的结果	结论
$B$ 是好的	$A$ 是好的	两片都是好的，或都是坏的
$B$ 是好的	$A$ 是坏的	至少一块是坏的
$B$ 是坏的	$A$ 是好的	至少一块是坏的
$B$ 是坏的	$A$ 是坏的	至少一块是坏的

  a. 证明：如果超过 $n/2$ 块芯片是坏的，使用任何基于这种逐对检测操作的策略，教授都不能确定哪些芯片是好的。假定坏芯片可以合谋欺骗教授。
  b. 考虑从 $n$ 块芯片中寻找一块好芯片的问题，假定超过 $n/2$ 块芯片是好的。证明：进行 $\lfloor n/2\rfloor$ 次逐对检测足以将问题规模减半。
  c. 假定超过 $n/2$ 块芯片是好的。证明：可以用 $\Theta (n)$ 次逐对检测找出好的芯片。给出描述检测次数的递归式，并求解它。

  证