2020 年第一届辽宁省大学生程序设计竞赛

记录一下3h写出来的几道题。

A-组队分配

题目描述
ACM团队为即将到来的省赛举行了一场校内选拔赛，这场比赛共有 $3n$ 个人参与，每个人在比赛中的排名已经给出。
现在团队希望按照排名分配，组成 $n$ 个队伍。组队的规则是：排名从 $1$ 到 $3n$ ，名次为 $3a+1,3a+2,3a+3...$ $a=0,1,2...$ 的人组成一个队伍，称为“ACM-‘a’”队，例如由第一名、第二名、第三名组成的队伍就叫“ACM-0”，由第四名、第五名、第六名组成的队伍就叫“ACM-1”。
现在给你这 $3n$ 个人的名字以及排名，需要聪明的你给出最终的组队方案。组队方案按照如下规则输出：每个队伍一行，按“队名 队员一姓名 队员二姓名 队员三姓名”的格式输出，要求每个队中的队员按照排名从大到小排列。

输入描述:
数据的第一行有一个 $t$ ，代表 $t$ 组数据
每组数据的第一行有一个 $n$，代表题目中的 $n$ 。$1\le n\le 4\ast 10^4，{\sum }_{}^{}n\le 5\ast 10^4$
接下来的 $3n$ 行，每一行由一个字符串 $s$ 和一个数字 $a$ 组成，$s$ 和 $a$ 由一个空格隔开，保证字符串中不含有空格。$1\le length(s)\le 20，1\le a\le 3n$
输出描述:
输出 $n$ 行，每行按照 “队名 队员一姓名 队员二姓名 队员三姓名” 的格式输出，行末无多余空格。

输入	输出
1 1 a 1 b 3 c 2	ACM-0 b c a

分析

一开始是直接读入姓名 $nod[i].name$ 和排名 $nod[i].rank$ ，在所有数据输入完毕后进行结构体排序，再考虑输出的问题，但这样会段错误。
实际上刚开始读入时就可以按照他们的排名进行读入就可以，这样就不会消耗结构体排序等不必要的操作。这样之后再考虑输出的内容就可以了~

代码

#include
#include
using namespace std;
typedef long long ll;
const ll maxn=1e6+10;
const ll mod=1e9+7;

int T,n;
string s;
int a;

struct node
{
	string name;
}nod[maxn];

int main()
{
	cin>>T;
	while(T--)
	{
		cin>>n;
		for(int i=0;i<3*n;i++)	//有3n个人
		{
			cin>>s>>a;
			nod[a].name=s;
		}
		for(int i=1;i<=3*n;i+=3)	//每个队三个人,排名从大到小输出
		{
			cout<<"ACM-"<<i/3<<" "<<nod[i+2].name<<" "<<nod[i+1].name<<" "<<nod[i].name<<"\n";
		}
	}
	return 0;
}

---

B-两点距离

题目描述
已知现在有 $n$ 个点，以 $1-n$ 标号，不同两点之间的距离为两点标号的最大公约数，求点 $x$ 到点 $y$ 的所需移动的最短距离。

输入描述:
第一行两个数 $n$，$q$ 。表示有 $n$ 个点，$q$ 组询问。$1\le n\le 10^7,1\le q\le 5\ast 10^5$
接下来 $q$ 行，每行两个数 $x，y$ 。$1\le x,y\le n$
输出描述:
每个询问输出一行，
每行一个数字表示答案。

输入	输出
5 2 1 1 2 4	0 2

分析

一开始想当然了，觉得两点之间的距离就是最短的。实际上不一定，因为点与点之间的边权值是两点标号的最大公约数，列出一定的数值可以发现：
① 当 $x=y$ 时，最短距离一定为 $0$ 。
② 当 $gcd(x,y)=1$ ，即 $x$ 和 $y$ 互质时，最短距离一定为 $1$ 。
③ 其他情况时，最短距离一定为 $2$ 。

这是因为，点 $x$ 到点 $y$ 的最短距离无非是直接到达或者是间接到达。两点距离是 $0$ 不用解释。而如果直接到的距离已经是 $1$ 了，不论间接的方式边权值再小，一定会比 $1$ 大，此时间接到就不合适了。但如果直接到的距离 $\ge 2$ ，一定能另外找到一个点 $z$ ，使得 $x-z$ 和 $z-y$ 的距离都为 $1$ ，因此最短距离为 $2$ 。
这里不再过多解释（自己打表举例子就可以发现了）。如输入的数据为 $“3$ $6”$，结果应该为 $2$ 。（可以 $3$ 到 $5$ ，$5$ 再到 $6$ 等）

代码

#include
using namespace std;
typedef long long ll;
const ll maxn=1e6+10;
const ll mod=1e9+7;

ll n,q,x,y;

ll gcd(ll a,ll b)	//最大公约数的模板
{
	return b==0?a:gcd(b,a%b);
}

int main()
{
	scanf("%lld%lld",&n,&q);
	while(q--)
	{
		scanf("%lld%lld",&x,&y);
		if(x==y)
		{
			printf("0\n");
			continue;
		}
		if(gcd(x,y)==1)
		{
			printf("1\n");
			continue;
		}
		printf("2\n");
	}
	return 0;
}

---

C-轮到谁了？

题目描述
在一个班级里面有 $m$ 个学生，每个人的学号是 $0$ 到 $m-1$ 的 $m$ 个数字。现在老师出了一道谜题，如果所有人都答出来，那么就只有谜底表示的人需要做作业，否则所有人都要做作业（显然大家都会积极的找出谜底，因为谁都不想写作业），谜题如下： 假设有一对兔子，长两个月它们就算长大成年了。然后以后每个月都会生出 $1$ 对兔子，生下来的兔子也都是长两个月就算成年，然后每个月也都会生出 $1$ 对兔子了。这里假设兔子不会死，每次都是只生 $1$ 对兔子。 第一个月只有一对刚出生的小兔子（标号为 $0$ ）。每对出生的兔子按照按照出生顺序 $0$ 到 $m-1$ 循环标号，前 $n$ 个月内出生的最后一对兔子的标号就是需要做作业的人的学号。你能找出谜底吗？

输入描述:
有 $T$ 组输入，每组数据输入一行。$(1\le T\le 50)$
每行两个整数 $n，m$ 。$(1\le m\le 500,1\le n\le 1000)$
输出描述:
每组数据输出一行，
每行一个数字，做作业人的标号。

输入	输出
4 3 20 5 4 1 10 2 10	1 0 0 0

分析

这题很像 HDU-2018 母牛的故事 。

若把一对兔子看作一个点，那么题中的情况就如下图所示：
（ $f(n)$ 代表第 $n$ 个月有几对兔子）

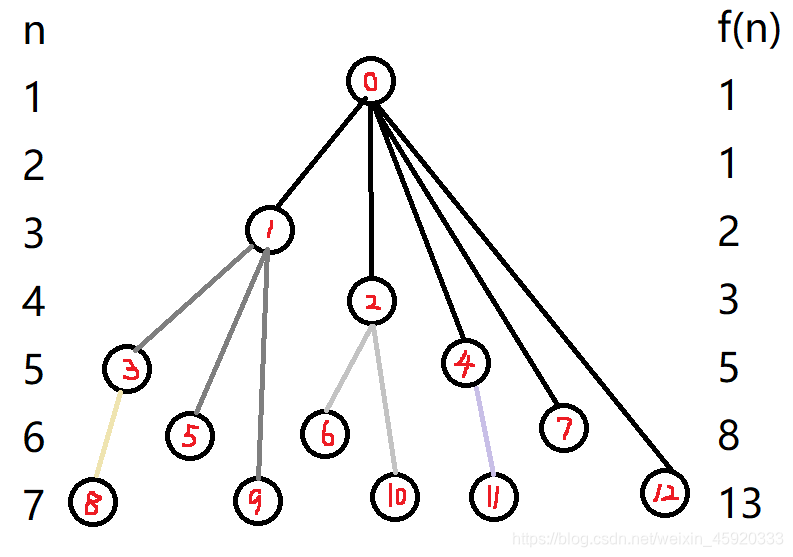
我们很容易发现 $f(n)$ 与斐波那契数列相当。
但如果直接斐波那契数列打表，最后才对 $m$ 取模会WA。因此只需要每组询问都重新计算 $f$ 数组的值就可以了。


最后才对 $m$ 取模会WA的原因：斐波那契数列到后面会越来越大，当 $n$ 的值很大时，$f(n)$ 的值会非常大，因此会溢出，从而对结果产生影响。

代码

#include
using namespace std;
typedef long long ll;
const ll maxn=1e3+10;
const ll mod=1e9+7;

int T,n,m;
ll f[maxn];	//兔子的对数

void fib()
{
	f[0]=f[1]=f[2]=1;
	for(int i=3;i<maxn;i++)
		f[i]=f[i-1]%m+f[i-2]%m;
}

int main()
{
	scanf("%d",&T);
	while(T--)
	{
		scanf("%d%d",&n,&m);
		fib();
		printf("%lld\n",(f[n]-1+m)%m);	//问的是最后一个点的编号
	}
	return 0;
}

---

F-最长回文串

题目描述
回文串是反转后与自身完全相同的字符串
比如：“ABA”,“ACMMCA”,“A”。
给出一系列长度相同的字符串，请按序进行如下操作构造出最长的回文串:

   1.舍弃一些字符串
   2.重新排列剩余的每个字符串内字符的顺序，重新排列后的结果可以与原字符串相同
   3.重新排列剩余字符串的顺序
   4.将剩余字符串按序首尾连接组成回文串

输入描述:
第一行输入两个整数 $n$ 和 $m$ $(1\le n\le 100,1\le m\le 50)$ ，表示字符串的数量和每个字符串的长度。
接下来 $n$ 行每行包含一个长度为 $m$ 的字符串，每个字符串由小写英文字母组成。
输出描述:
每组数据输出一个整数，表示经过以上四次操作你能够得到的最长回文串的长度。

输入	输出
3 3 tab one abt	6

分析

由于最后只需要考虑能得到的最长回文串的长度是多少，因此我们只需要考虑普遍规律。
我们可以想到：
① 若两个字符串的字符个数且类型完全相同（不考虑字符排列顺序），那么这两个字符串肯定是要的，因为经过字符串内部字符交换顺序的操作，这两个字符串可以分别放在新字符串的首尾，此时一定是个回文串。
② 若一个字符串与其他字符串的字符个数或类型不同（不考虑字符排列顺序），就需要考虑该字符串本身是否是回文串。若它是回文串，则要了这个字符串，因为它可以放在新字符串的中间；若它不是，则把它删去，因为它放在哪都会导致新字符串不是回文串。

由于不考虑字符串内部字符的顺序，我们可以从一开始就对字符串本身进行排序，然后用 $map$ 记录这种字符串的个数，若个数为 $2$ ，则增加 $sum$ 的值，并让 $mp[s]$ 的值重新赋为 $0$ 。如有三个字符串 $“abc”$ ，只能构成回文串 $“abccba"$ 等格式，不能让第三个 $“abc”$ 也加入，除非这个字符串本身就是回文串。

判断一个交换过字符顺序后的字符串是否可以是回文串，需要先考虑该字符串的长度是否为偶数：
① 若字符串长度为偶数，则只需要两个两个字符遍历，查看这两个字符是否相等，若不相等则不可以是回文串；若直到最后都是相等的，则可以是回文串。
② 若字符串长度为奇数，则需要遍历整个字符串，记录每个字符出现的次数。若出现的次数为偶数，则不记录；若出现的次数为奇数，则记录有几个字符出现的次数是奇数，如果有超过一个字符出现的次数为奇数，则说明该字符串不可以是回文串，否则就是回文串。如 $“abbbc"$ 不可以是回文串， $“aabbb”$ 可以是回文串。

需要注意的是，若考虑完了条件①后，有好几个字符串满足条件②，我们只需要取一个回文串。这是因为好几个回文串在一起并不能形成一个新的回文串，若它们可以形成一个新的回文串，应该会满足条件②。如字符串 $“abc”$和字符串 $“abd”$ ，在不修改、删除字符串内部字符的前提下，是无论如何都不能成为一个回文串的。

代码

#include
#include
#include
#include
using namespace std;
typedef long long ll;
const ll maxn=1e3+10;
const ll mod=1e9+7;

int n,m,flag;
ll sum;
string s;
map<string,int> mp;
map<char,int> mmp;

bool judge(string s)	//判断是否为回文串
{
	int len=m;
	bool ff=true;
	if(len&1==0)	//字符串为偶数
	{
		for(int i=1;i<len;i+=2)
		{
			if(s[i]!=s[i-1])
			{
				ff=false;
				break;
			}
		}
	}
	else
	{
		int cnt=0;
		for(int i=0;i<len;i++)	//记录每个字符出现的次数
		{
			mmp[s[i]]++;
		}
		for(auto itt:mmp)
		{
			if(cnt>1)
			{
				ff=false;
				break;
			}
			if(itt.second%2==1)
			{
				cnt++;
			}
		}
	}
	if(ff)	return true;
	return false;
}

int main()
{	
	cin>>n>>m;
	sum=0;
	for(int i=1;i<=n;i++)
	{
		cin>>s;
		sort(s.begin(),s.end());
		mp[s]++;
		if(mp[s]==2)
		{
			sum+=2;
			mp[s]=0;
		}
	}
	flag=0;
	for(auto it:mp)	//看看剩下的字符串中是否还有回文串
	{
		if(flag)	break;	//已经找到了一个回文串
		if(it.second)
		{
			if(judge(it.first))
			{
				flag=1;
				break;
			}
		}
	}
	cout<<(sum+flag)*m<<endl;
	return 0;
}

---

G-管管的幸运数字

题目描述
总所周知，每个人都有自己的幸运数字，而管管的幸运数字是除了 $1$ 和它自身外，不能被其他自然数整除的数，管管现在有 $T$ 次询问，每次询问会给定一个数字 $N$ ，你需要告诉他 $N$ 是不是他的幸运数字，如果不是，需要你告诉他离 $N$ 最近的幸运数字 $L$ 与 $N$ 差的绝对值 即 $|L-N|$ 。

输入描述:
第一行含有一个整数 $T(T\le 100)$ 表示询问次数。
对于每次询问，第一行含有一个整数 $N(1<N\le 10000)$ 表示管管向你询问的数字。
输出描述:
对于每次询问，如果 $N$ 是管管的幸运数字则输出 $YES$ ，否则输出离 $N$ 最近的幸运数字 $L$ 与 $N$ 差的绝对值 $|L-N|$ 。

输入	输出
3 3 4 10	YES 1 1

分析

这里我用到了线性筛+二分的思想。
由题意可知：管管的幸运数字是质数，若 $N$ 为质数，则直接输出 $“YES”$ ，否则就需要找到离 $N$ 最近的质数 $L$ 与 $N$ 的差值 $|L-N|$。

一开始看见要先判断质数就条件反射性地想起了线性筛。正好线性筛中的 $prime$ 数组会存放 $＜maxn$ 的所有质数。因此若 $N$ 为质数，则直接输出；若 $N$ 不是质数，则利用二分找到 $\le N$ 的最大的质数 $L$ ，将它在 $prime$ 数组中的下标记录到变量 $tt$ 中。此时还需要判断一下是离 $N$ 最近的左边的质数到 $N$ 的距离小还是 $N$ 最近的右边的质数到 $N$ 的距离小，输出小的那个。而因为我们已经找到了左边的质数 $prime[tt]$ ，右边的质数就是 $prime[tt+1]$ 。

代码

#include
using namespace std;
typedef long long ll;
const ll maxn=1e6+10;
const ll mod=1e9+7;

int T,N;

bool isprime[maxn];
int prime[maxn/10],m;
void primes()	//线性筛
{
	isprime[0]=isprime[1]=true;
	for(int i=2;i<maxn;i++)
	{
		if(!isprime[i])
			prime[++m]=i;
		for(int j=1;i*prime[j]<maxn && j<=m;j++)
		{
			isprime[i*prime[j]]=true;
			if(i%prime[j]==0)	break;
		}
	}
}

int main()
{
	scanf("%d",&T);
	primes();
	while(T--)
	{
		scanf("%d",&N);
		if(!isprime[N])	//N是质数
		{
			printf("YES\n");
			continue;
		}
		int l=0,r=m,mid,tt;
		while(l<=r)
		{
			mid=(l+r)>>1;
			if(prime[mid]<=N)
			{
				tt=mid;
				l=mid+1;
			}
			else
			{
				r=mid-1;
			}
		}
		int at=N-prime[tt];	//左边的质数与N的距离
		int bt=prime[tt+1]-N;	//右边的质数与N的距离
		if(at>bt)	printf("%d\n",bt);
		else	printf("%d\n",at);
	}
	return 0;
}

---

I-鸽子的整数运算

题目描述
众所周知金鱼的记忆只有七秒，而鸽子们的记性也不太好（不然怎么会经常放别人鸽子），所以对于鸽子们来说数学运算太难了，而开学前的最后一天某位不愿透露姓名的鸽子突然跑来找你，想让你帮他解决他的寒假作业，你看到这个厚达 $1e9+7$ 页的作业，陷入了沉思。机智的你很快就想到用程序去批量完成，现在作业里面有这么些题型： $1.a+b$ $2.a-b$ $3.a\ast b$ $4.a/b$（整型除法，向下取整） 机智的你一定知道怎么完成这个任务，你能帮帮这位可怜的鸽子吗？

输入描述:
第一行一个数字 $T(1\le T\le 1000)$ 表示组数接下来 $T$ 行
每一行包括一个整数 $op(op\in \{1,2,3,4\})$ ，以及两个整数 $a,b(0<a,b\le 100)$ , $op$ 代表操作类型，具体操作与题目表述中一致。
输出描述:
见题目表述

输入	输出
4 1 2 3 2 2 3 3 2 3 4 2 3	5 -1 6 0

分析

签到题，按照题目中所述的方法进行分类讨论就可以。

代码

#include
using namespace std;
typedef long long ll;
const ll maxn=1e6+10;
const ll mod=1e9+7;

int T,op,a,b;

int main()
{
	scanf("%d",&T);
	while(T--)
	{
		scanf("%d%d%d",&op,&a,&b);
		if(op==1)
		{
			printf("%d\n",a+b);
		}
		else if(op==2)
		{
			printf("%d\n",a-b);
		}
		else if(op==3)
		{
			printf("%d\n",a*b);
		}
		else
		{
			printf("%d\n",a/b);
		}
	}
	return 0;
}