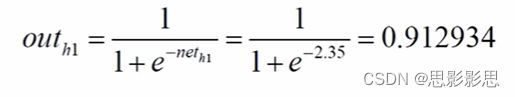【无标题】
| 时间 | 版本 | 修改人 | 描述 |
|---|---|---|---|
| 2023年11月6日20:54:13 | V0.1 | 宋全恒 | 新建文档 |
简介
在神经网络的世界中,参数和权重是非常重要的概念,尤其是当下,大模型横行其道,ChatGPT,文心一言,通义千问等各种领域的大模型接二连三的诞生,而大模型大就大在神经网络结构复杂,参数量非常庞大。
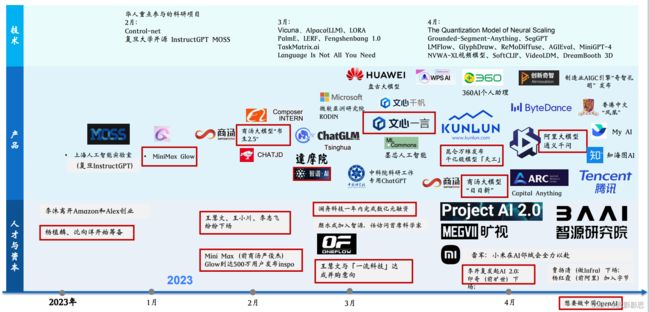
不同的大模型,参数是非常巨大的。这是一场参数为王的战争。在神经网络的世界中,参数和权重的更新有一个核心算法,就是BP算法(神经网络之父:杰弗瑞·欣顿提出的反向传播算法 Back Propagation,解决了两层神经网络所需要的复杂计算问题),也就是反向传播算法。BP算法它解决的问题是参数如何更新的问题。
神经网络结构在训练的过程中不断的进行前向传播和反向传播,前向传播得到预期结果,当然更重要的是得到误差,然后反向传播将误差一层一层的传播到每一层进而更新参数的权重。神经网络的训练也就是在前后,前后的交替中得以训练到稳定的状态的。
文章采用的是东方耀的B站视频,理解实践得出,对于BP的算法较为透彻的理解,读者也可以去理解一下,对于理解BP算法的过程也是非常的有帮助的。

感知机
巨大的神经网络结构,在结构上有一个最小,也是最重要的结构就是感知机Perceptron。
感知机是一种将特征空间的向量x映射到1, -1二值的线性分类模型,分类函数通过对训练集使用梯度下降算法求解得到:
在之前的博客 10-09 周一 图解机器学习之深度学习感知机学习中,我们已经通过使用感知机来逻辑和(and)函数的运算。这也是最为简单的浅层神经网络,输入层只有两个神经元,一个输出神经元。
神经网络结构如下所示:
![]()
但是这样的浅层神经网络问题在面对简单的异或问题都会束手无策,但随着层数的增多,神经网络表现出强大的能力,但随之而来的则是巨大的计算量,好在现代的GPU等算力计算能力越来越快,曾经困扰着那个时代的科学家,现在可以非常容易的使用神经网络解决自己遇到的科学问题。
神经网络计算过程
神经网络初始结构
一个复杂的神经网络结构如下所示:
上述过程中,给出了神经网络14个参数的初始权重,以及两个输出的实际值(0.01, 0.99)。输入样本为(5, 10)。神经网络一共三层,输入层两个神经元,一个隐藏层,隐藏层一共两个节点,两个输出层神经元。
前向传播计算
根据上图,首先,我们要根据样本和w1-w6计算出h1到h3的输入和输出。此时我们以neth1, outh1来表示h1神经元的输入,其中neth1表示输入的加权和,outh1经过激活函数之后的值。在计算时得到如下的公式:
所以
neth1=w1 * I1 + w2 * I2+b1 1 = 0.1 * 5 + 0.1510 + 0.35 * 1 = 2.35.
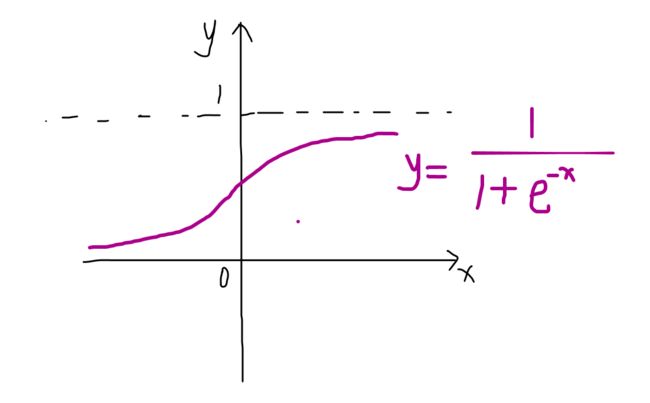
为了计算outh1,需要选择一个激活函数,增加神经网络的非线性能力,我们选择最常用的sigmoid函数。
因此,我们可以计算得出:
outh1 = 0.912934227559729
根据类似的计算方法,我们依次得到neth2, outh2, neth3, outh3。
neth2 = w3 * I1 + w4 * I2 + b1 * 1 = 0.2 * 5 * 0.25 * 10 + 0.35 * 1 = 3.85.
outh2 = 0.97916365548132
neth3 = w5 * I1 + w6 * I2 + b1 * 1 = 0.3* 5 + 0.35 * 10+ 0.35 * 1 = 5.35
outh3 = 1/(1+exp(-neth3)) = 0.995274287397605
至此,我们已经能够得到隐藏层三个神经元的全部输入和输出了,以同样的方式,我们再次计算从隐藏层到输出层的加权和和预测值。
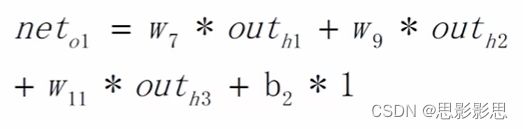
neto1=w7 * h1 + w9 * h2+w11*h3+b2 *1 =
0.4 * 0.912934227559729 + 0.5 * 0.97916365548132 + 0.6 * 0.995274287397605 + 0.65 * 1= 2.10192009120311
outo1 = 1/(1+exp(-2.10192009120311)) = 0.891089661476517
可以看到神经元o2的加权和有3个隐藏层神经元有贡献,计算公式与neto1类似,不再赘述。
neto2 = w8 * outh1 + w10 * outh2 + w12 * outh3 + b2 *1 =
= 0.45 * 0.912934227559729 + 0.55 * 0.97916365548132 + 0.65 * 0.995274287397605 + 0.65 =
2.24628869972505
outo2 = 1/(1+exp(-2.24628869972505)) = 0.904329924850017。
由此,我们已经完成了前向传播得到了输出为(0.891089661476517, 0.904329924850017) 与实际值(0.01, 0.99)的误差相对还是挺大的,采用均方误差的公式,可以得到总的误差为:
Etotal = E1 + E2 = 1/2*[(0.01-0.891089661476517)2+(0.99-0.904329924850017)2] = 1/2[(0.881089661476517)2+(-0.0856700751499829)2] = 0.39182917666850353
注意,指数运算和平方运算的函数区别。
反向传播
从前向传播,我们可以得到模型的预测值和实际值之间的差距,这也称为误差或者损失,我们的核心目标是通过调整权重参数降低这个误差,方法就是通过梯度下降来求解。本质是通过求偏导得出的。
其实就是求导数。使用方法就是链式求导的法则。
首先,我们计算出Etotal对于w7这个变量的偏导,相当于假定其他的均为常量进行计算。
学习率是深度学习中的一个重要的超参数,如何
调整学习率是训练出好模型的关键要素之一。学习率太大容易出现超调现象,即在极值点两端不断发散,或是剧烈震荡,总之随着迭代次数增大loss没有减小的趋势;太小会导致无法快速地找到好的下降的方向,随着迭代次数增大loss基本不变。学习率越小,损失梯度下降的速度越慢,收敛的时间更长。
新权值 = 当前权值 – 学习率 × 梯度。
隐藏层到输出层
从隐藏层到输出层一共涉及了7个参数,即w7–w12和b2.
基本思路也是求出总的误差相当于各个参数的偏导,这样确定参数的变化方向。
注: 计算的关键在于sigmoid函数求导在数学上有着特殊的性质。以及链式求导和函数求导的性质。
下图中也给出了对于隐藏层的偏置参数b2的更新,基本思路是一样的。
输入层到隐层
从输入层到隐层要使用已经更新过的权重参数w7-w12,同时由于输入层的参数,如w1影响了neth1,进而会同时影响neto1和neto2,进而影响outo1和outo2,影响了总的误差。所以在在计算上更加复杂。
注,上述的计算过程公式没有问题,但是结果存在问题。
代码演示
下面是围绕着单个样本,来不断的调整权重参数的代码示例。
import numpy as np
w=[0, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65]
# 偏置
b=[0, 0.35, 0.65]
# 实际值
target=[0, 0.01, 0.99]
# 样本
s=[0, 5, 10]
def sigmoid(x):
return 1/(1+np.exp(-x))
print(sigmoid(0))
def bp(s, w, b, target):
# 前向传播求误差
h1 = sigmoid(w[1]*s[1] + w[2]*s[2]+b[1])
h2 = sigmoid(w[3]*s[1]+w[4]*s[2] + b[1])
h3 = sigmoid(w[5]*s[1] + w[6]*s[2] + b[1])
print(f"隐层输出h1={h1}, h2={h2}, h3={h3}")
o1 = sigmoid(w[7]*h1+w[9]*h2+w[11]*h3 + b[2])
o2 = sigmoid(w[8]*h1+w[10]*h2+w[12]*h3 + b[2])
print(f"输出层: o1={o1}, o2={o2}")
e1 = 1/2*np.square(target[1]-o1)
e2 = 1/2*np.square(target[2]-o2)
e = e1 + e2
print(f"总误差为: {e}")
print(f"更新前:w[7]-w[12] {w[7:12]}")
# 提取共同的因子
t1 = -1*(target[1]-o1)*o1*(1-o1)
t2 = -1*(target[2]-o2)*o2*(1-o2)
# 反向传播更新权重
w[7] = w[7] - 0.5 * t1*h1
w[8] = w[8] - 0.5 * t2*h1
w[9] = w[9] - 0.5 * t1*h2
w[10] = w[10] - 0.5 * t2*h2
w[11] = w[11] - 0.5 * t1*h3
w[12] = w[12] - 0.5 * t2*h3
print(f"更新后: w[7]-w[12] {w[7:12]}")
print(f"更新前: w[1]-w[6] {w[1:6]}")
w[1] = w[1] - 0.5 * (t1*w[7]+ t2*w[8])*h1*(1-h1)*s[1]
w[2] = w[2] - 0.5 * (t1*w[7]+ t2*w[8])*h1*(1-h1)*s[2]
w[3] = w[3] - 0.5 * (t1*w[9]+ t2*w[10])*h2*(1-h2)*s[1]
w[4] = w[4] - 0.5 * (t1*w[9]+ t2*w[10])*h2*(1-h2)*s[2]
w[5] = w[5] - 0.5 * (t1*w[11]+ t2*w[12])*h3*(1-h3)*s[1]
w[6] = w[6] - 0.5 * (t1*w[11]+ t2*w[12])*h3*(1-h3)*s[2]
print(f"更新后: w[1]-w[6] {w[1:6]}")
return o1, o2, e, w
for i in range(1001):
print(f"第{i}轮")
o1, o2, e, w = bp(s, w, b, target)
代码运行日志如下:
第0轮
隐层输出h1=0.9129342275597286, h2=0.9791636554813196, h3=0.9952742873976046
输出层: o1=0.8910896614765176, o2=0.9043299248500164
总误差为: 0.3918291766685041
更新前:w[7]-w[12] [0.4, 0.45, 0.5, 0.55, 0.6, 0.65]
更新后: w[7]-w[12] [0.3609680622498306, 0.4533833089635062, 0.4581364640581681, 0.5536287533891512, 0.5574476639638248, 0.653688458944847]
更新前: w[1]-w[6] [0.1, 0.15, 0.2, 0.25, 0.3, 0.35]
更新后: w[1]-w[6] [0.09453429502265628, 0.13906859004531255, 0.1982111758493806, 0.24642235169876123, 0.29949648483800345, 0.34899296967600685]
第1轮
隐层输出h1=0.9014426112099272, h2=0.9782314364856383, h3=0.9952147111775244
输出层: o1=0.8785036242317737, o2=0.9047226616148428
总误差为: 0.3807853848728913
更新前:w[7]-w[12] [0.3609680622498306, 0.4533833089635062, 0.4581364640581681, 0.5536287533891512, 0.5574476639638248, 0.653688458944847]
更新后: w[7]-w[12] [0.3191863144400141, 0.45669650253339406, 0.4127955641821147, 0.5572241792819611, 0.5113195915142353, 0.6573463057569756]
更新前: w[1]-w[6] [0.09453429502265628, 0.13906859004531255, 0.1982111758493806, 0.24642235169876123, 0.29949648483800345, 0.34899296967600685]
更新后: w[1]-w[6] [0.08870805617036942, 0.12741611234073882, 0.19639207886219862, 0.24278415772439726, 0.2989896817160982, 0.34797936343219626]
第10轮
隐层输出h1=0.8522931631204915, h2=0.973666035904956, h3=0.9948605448366504
输出层: o1=0.6182485982291118, o2=0.9098574910079107
总误差为: 0.18819458949761328
更新前:w[7]-w[12] [-0.10761926674458068, 0.48082572625849623, -0.08313002065013501, 0.5851569288735385, 0.004809785641267411, 0.6858692203369033]
更新后: w[7]-w[12] [-0.1687956652929053, 0.48362680269767216, -0.15301839244864018, 0.5883568993893336, -0.06659989805031236, 0.6891388469782868]
更新前: w[1]-w[6] [0.07610804313549309, 0.10221608627098615, 0.190408353976401, 0.230816707952802, 0.2966262198756943, 0.34325243975138864]
更新后: w[1]-w[6] [0.08473485099950548, 0.11946970199901091, 0.19206435622781262, 0.23412871245562528, 0.2968063347643646, 0.3436126695287292]
第100轮
隐层输出h1=0.9891236087215748, h2=0.9921661778960364, h3=0.9963896678436679
输出层: o1=0.07388936805924926, o2=0.9458649137665609
总误差为: 0.003014878593921662
更新前:w[7]-w[12] [-1.0850594180486732, 0.6369390234749703, -1.0964255065626485, 0.7437262476913241, -1.021016770363603, 0.8457592597174984]
更新后: w[7]-w[12] [-1.087221608708466, 0.6380566906609282, -1.0985943481754594, 0.744847352849743, -1.023194844382188, 0.8468851372381206]
更新前: w[1]-w[6] [0.1864089921965286, 0.3228179843930571, 0.23965760338038153, 0.3293152067607631, 0.3108135454268529, 0.3716270908537057]
更新后: w[1]-w[6] [0.1865756139120173, 0.3231512278240345, 0.23978363897681412, 0.3295672779536283, 0.3108709873105615, 0.37174197462112285]
第1000轮
隐层输出h1=0.9946371958223346, h2=0.9955975672745342, h3=0.9973483220036176
输出层: o1=0.022970938311877513, o2=0.9776754532055207
总误差为: 0.00016006984718992034
更新前:w[7]-w[12] [-1.489582973447391, 0.9415807254516165, -1.5016742512504941, 1.0488846306039166, -1.4274137106156801, 1.1517468039990286]
更新后: w[7]-w[12] [-1.4897277480268165, 0.9417145029348198, -1.501819165616943, 1.0490185372559027, -1.4275588798135195, 1.151880946125379]
更新前: w[1]-w[6] [0.21491564150393844, 0.3798312830078768, 0.2628474338690681, 0.3756948677381351, 0.3231962973308205, 0.3963925946616401]
更新后: w[1]-w[6] [0.21492480264567834, 0.3798496052913566, 0.26285531655106104, 0.37571063310212094, 0.32320109359763793, 0.396402187195275]
上述代码给出了在运行状态下的几轮日志,方便理解和验证程序。
总结
终于把这个深度学习的BP算法,自己手敲了一遍,对于前向传播和反向传播理解更加具体了一些。另外,可以看到,我们在计算时,仅仅保留了每个节点的输出,即经过激活函数作用之后的值。并没有保存加权和的值。样例程序是非常简单的结构,仅仅有14个参数,另外需要注意的是,偏置项b[1]和b[2]并没有作为待更新的权重参数而存在,而是作为常量在代码中演示了。笔者尝试在图片中给出了偏置项的更新公式,基本上也是非常简单的。并不难理解。