代码随想录算法训练营第11天|20. 有效的括号 1047. 删除字符串中的所有相邻重复项 150. 逆波兰表达式求值

JAVA代码编写

20. 有效的括号

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

1. 左括号必须用相同类型的右括号闭合。
2. 左括号必须以正确的顺序闭合。
3. 每个右括号都有一个对应的相同类型的左括号。

示例 1：

输入：s = "()"
输出：true

示例 2：

输入：s = "()[]{}"
输出：true

示例 3：

输入：s = "(]"
输出：false

提示：

• 1 <= s.length <= 104
• s 仅由括号 '()[]{}' 组成

教程：https://programmercarl.com/0020.%E6%9C%89%E6%95%88%E7%9A%84%E6%8B%AC%E5%8F%B7.html#%E6%80%9D%E8%B7%AF

视频：https://www.bilibili.com/video/BV1AF411w78g/

方法一：

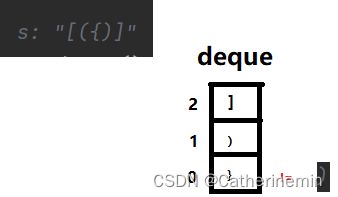
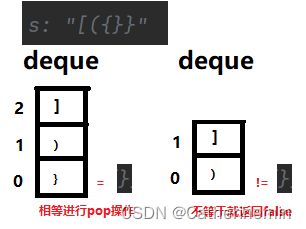
思路：将左括号对应的右括号进队

判断条件很巧妙，一下看不明白。

deque.isEmpty() || deque.peek() != ch:表示deque是空的或者deque的第一个元素与当前遍历的字符不等，就返回false；

来举例说明：

情况1：

情况2：

情况3：

复杂度分析：

• 时间复杂度: $O(n)$

• 空间复杂度:$O(n)$，n为s长度

import java.util.Deque;
import java.util.LinkedList;

public class Solution {
    public boolean isValid(String s) {
        Deque<Character> deque = new LinkedList<>();//定义一个双端队列
        char ch;
        for (int i = 0; i < s.length(); i++) {
            ch = s.charAt(i);
            //碰到左括号，就把相应的右括号入栈
            if (ch == '(') {
                deque.push(')');
            }else if (ch == '{') {
                deque.push('}');
            }else if (ch == '[') {
                deque.push(']');
            } else if (deque.isEmpty() || deque.peek() != ch) {
                return false;
            }else {//如果是右括号判断是否和栈顶元素匹配
                deque.pop();
            }
        }
        //最后判断栈中元素是否匹配
        return deque.isEmpty();
    }

    public static void main(String[] args) {
        Solution solution = new Solution();
        solution.isValid("()[]{}");
    }
}

Double Ended Queue相关

• Deque 是一个双端队列（Double Ended Queue）的接口，它继承自 Queue 接口，并且支持在队列的两端进行插入和删除操作。其中 Character 是指双端队列中存储的元素类型为字符类型。

• 双端队列（Double Ended Queue，简称Deque）是一种具有队列和栈的特性的数据结构，支持在队列头部和尾部进行插入和删除操作。

• Deque 接口中的 peek() 方法用于获取双端队列的第一个元素，但并不会将该元素从队列中移除。

• Deque 接口中的 push() 方法，它用于将元素推入双端队列的头部。即新元素会被插入到队列的最前面位置。

• Deque 接口中的 pop() 方法用于弹出双端队列的头部元素，并将该元素从队列中移除。

1047. 删除字符串中的所有相邻重复项

给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

在 S 上反复执行重复项删除操作，直到无法继续删除。

在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

示例：

输入："abbaca"
输出："ca"
解释：
例如，在 "abbaca" 中，我们可以删除 "bb" 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca"，其中又只有 "aa" 可以执行重复项删除操作，所以最后的字符串为 "ca"。

提示：

1. 1 <= S.length <= 20000
2. S 仅由小写英文字母组成。

教程：https://programmercarl.com/1047.%E5%88%A0%E9%99%A4%E5%AD%97%E7%AC%A6%E4%B8%B2%E4%B8%AD%E7%9A%84%E6%89%80%E6%9C%89%E7%9B%B8%E9%82%BB%E9%87%8D%E5%A4%8D%E9%A1%B9.html

视频：https://www.bilibili.com/video/BV12a411P7mw

方法一：

思路：用栈比较好，先进后出。

每进栈，就和前一个元素比较，相等则把上一个元素出栈，否则就进栈；还需判别一下栈是否为空的情况，为空就进栈。

因为栈只能取栈顶元素，出栈就是结果的逆序。这样要新建一个栈，进栈，然后再赋给StringBuilder。

复杂度分析：

• 时间复杂度: $O(n)$
• 空间复杂度:$O(n)$，n为s长度

class Solution {
    public String removeDuplicates(String s) {
        Stack<Character> mystack = new Stack<>();
        char ch;

        for (int i = 0; i < s.length(); i++) {
            ch=s.charAt(i);
            if(mystack.isEmpty()||mystack.peek()!=ch){
                mystack.push(ch);
            }else{
                mystack.pop();
            }
        }

        Stack<Character> stack1 = new Stack<>();
        while (!mystack.isEmpty()) {
            stack1.push(mystack.pop());//mystack栈顶元素进新栈
        }

        StringBuilder sb = new StringBuilder();
        while (!stack1.isEmpty()) {
            sb.append(stack1.pop());
        }

        return sb.toString();
    }
}

150. 逆波兰表达式求值

给你一个字符串数组 tokens ，表示一个根据 逆波兰表示法 表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。

注意：

• 有效的算符为 '+'、'-'、'*' 和 '/' 。
• 每个操作数（运算对象）都可以是一个整数或者另一个表达式。
• 两个整数之间的除法总是 向零截断 。
• 表达式中不含除零运算。
• 输入是一个根据逆波兰表示法表示的算术表达式。
• 答案及所有中间计算结果可以用 32 位 整数表示。

示例 1：

输入：tokens = ["2","1","+","3","*"]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例 2：

输入：tokens = ["4","13","5","/","+"]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

示例 3：

输入：tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出：22
解释：该算式转化为常见的中缀算术表达式为：
  ((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

提示：

• 1 <= tokens.length <= 104
• tokens[i] 是一个算符（"+"、"-"、"*" 或 "/"），或是在范围 [-200, 200] 内的一个整数

逆波兰表达式：

逆波兰表达式是一种后缀表达式，所谓后缀就是指算符写在后面。

• 平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。
• 该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。

逆波兰表达式主要有以下两个优点：

• 去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
• 适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中

教程：https://programmercarl.com/0150.%E9%80%86%E6%B3%A2%E5%85%B0%E8%A1%A8%E8%BE%BE%E5%BC%8F%E6%B1%82%E5%80%BC.html

视频：https://www.bilibili.com/video/BV1kd4y1o7on/

方法一：

思路：

复杂度分析：

• 时间复杂度: $O(n)$

• 空间复杂度:$O(n)$

class Solution {
    public int evalRPN(String[] tokens) {
        Deque<Integer> stack = new LinkedList();
        for (String s : tokens) {
            if ("+".equals(s)) {// leetcode 内置jdk的问题，不能使用==判断字符串是否相等
                stack.push(stack.pop() + stack.pop());      // 注意 - 和/ 需要特殊处理
            } else if ("-".equals(s)) {
                stack.push(-stack.pop() + stack.pop());
            } else if ("*".equals(s)) {
                stack.push(stack.pop() * stack.pop());
            } else if ("/".equals(s)) {
                int temp1 = stack.pop();
                int temp2 = stack.pop();
                stack.push(temp2 / temp1);
            } else {
                stack.push(Integer.valueOf(s));
            }
        }
        return stack.pop();
    }
}