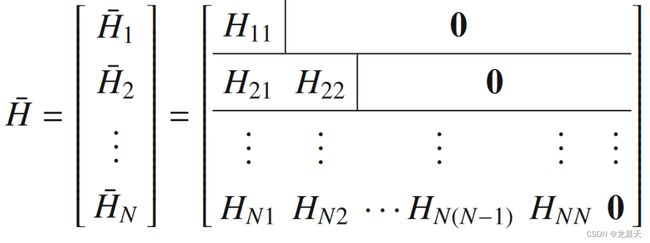LTI多智能体系统中分布式观测器的设计概述
LTI多智能体系统中分布式观测器的设计概述
摘要
随着信息技术和云计算的快速发展,传感器网络在我们的社会中发挥着越来越重要的作用。在过去的几十年里,分布式观测器理论由于其在不同领域的广泛潜在应用而受到前所未有的关注。与此同时,人们提出并研究了各种方法和算法。分布式观测器的设计是系统与控制研究的前沿课题之一,具有重要的理论价值和广阔的应用前景。本文试图回顾线性时不变(LTI)系统中分布式观测器设计的代表性模型和相应方法。首先,简要回顾了分布式观测器设计的研究背景和主要进展。然后,分别详细介绍了离散时间和连续时间LTI多智能体系统(MAS)分布式观测器设计的最新成果。最后提出了分布式观测器设计的展望和未来的工作方向。本文的主要目的是促进分布式观测器设计的新兴主题,重点关注技术科学的跨学科兴趣。
链接:An overview on the designs of distributed observers in LTI multi-agent systems | SpringerLink
介绍
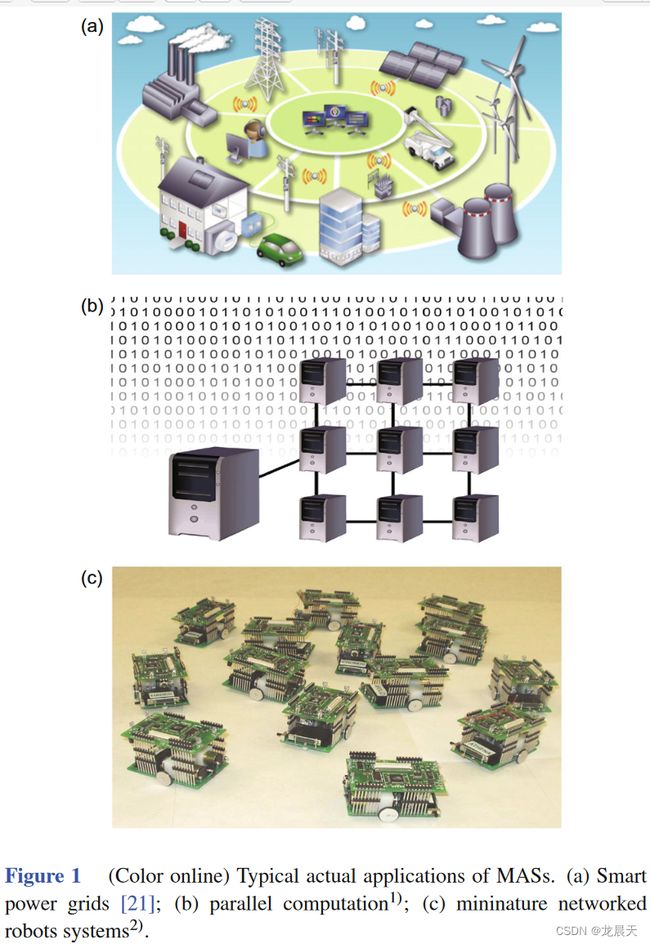
随着传感器信息技术的快速发展,网络化系统越来越广泛地存在于自然界和社会中。例子包括神经元网络、基因调控网络、社交网络、无线传感器网络、智能电网、生态网络和互联网[1-4]。在过去的几十年里,动态网络系统由于在数学、物理、生物学、工程和系统科学等各个学科中发挥着重要作用,已成为一个巨大的研究热潮[5-9]。近年来,在研究动态系统的拓扑结构[10, 11]、一致性[12, 13]、同步[14, 15]、分布式稳定[16]和协作控制[17,18]方面取得了许多突出成果。网络系统。当代仿生学的进展表明,动力网络系统中集体行为的研究不仅有助于揭示和分析自然界集体现象的内在机制,而且有助于解决现实工程系统领域的许多技术问题。例如,为了探索具有合作-竞争相互作用的多个欧拉-拉格朗日系统的集群行为,根据参考文献中系统的输入输出特性提出了一种辅助系统方法。 [19]。多智能体系统作为一种典型的动态网络系统,在理论研究和实际应用中引起了广泛的关注和广泛的研究[20, 21]。多智能体系统(MAS)的一些典型实际应用如图1所示。
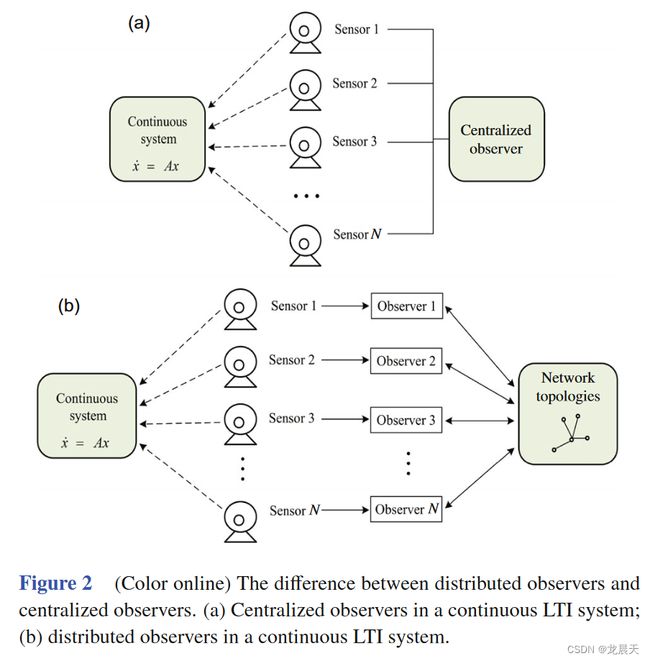
可控性和可观测性是控制理论和工程的基本问题[22, 23]。一般来说,对于实际的工程控制问题,所有的状态信息都不能直接测量并用于反馈。为了解决这个问题,提出了一种通用策略来设计完全状态观测器,并利用观测到的输出信息渐近地估计系统的状态信息。 Luenberger 的开创性工作首先提出了观测器的概念[24]。随后,针对不同类别系统的观测器设计进行了大量研究[25-28]。传统中心化观测器的主要特点是可以获取系统的完整输出信息。然而,在许多实际情况下,当系统维数较大时,需要部署大量观测器来观测状态,完整的输出信息通常是通过分布式传感器网络来测量的,单个观测器可能无法能够访问完整的输出信息。在这种情况下,传统的中心化观测器面临着很大的存储压力。可以设计一个合作观测器网络,其中每个观测器接收系统输出信息的一部分。分布式观测器和集中式观测器的区别如图2所示。
近年来,人们在分布式观测器的设计和分析方面做出了大量的努力,例如分布式估计、分布式卡尔曼滤波器和分布式状态观测器。 2005年,Olfati-Saber[29]首先提出了传感器网络的分布式卡尔曼滤波(DKF)。不久之后,帕克等 [30]导出了观测器参数存在的充分条件。他们提出了两步策略,一是卡尔曼滤波器估计更新步策略,二是数据融合步策略。然后,根据这两个步骤策略进行了许多其他研究。对于卡尔曼分布式滤波器步骤策略,参考文献。 [31-33]研究了传感器网络的能力和稳定性。参考文献[31]研究了具有分布式噪声测量的动态系统在非凸条件下的性能。参考文献[32]提出了一种基于矩阵空间分解的方法。参考文献[33]考虑了离散时间线性系统的 H2/H∞ 优化框架。对于数据融合步骤策略,观测器结构的研究主要集中在如何选择损失较小的估计-数据融合。加权平均[34]和八卦算法[35]是提出批准该结构的两种方法。与两步策略相比,参考文献中提出了采用增广态观测器设计的单时间尺度策略。 [28],并推导了全知参数设计的充要条件。
与上面提到的方法不同,分布式观测器是在参考文献[36-38]中提出的。图2(b)显示了连续线性时不变(LTI)系统中分布式观测器的机制。由于系统状态只能通过与邻居交互以及系统的部分输出来观察,因此设计分布式观察器非常重要。一方面,受领导者跟随MAS研究的启发[39, 40],观测器和控制器的每个状态都可以看作MAS的智能体状态;因此,设计分布式观测器的问题可以转化为MAS的领导者跟随一致性问题。另一方面,可以从系统可观测性分解的角度来设计观测器。 2015年,李等 [41]为线性MAS设计了完全分布式一致性协议,并提出了一种自适应算法来更新增益参数。金等 [42]设计了连续时间线性动力系统的Luenberger型状态观测器的分布式方案。随后,他们提出了基于可观测性分解的完全分散式设计,通过在每个节点和系统矩阵中进行可观测性分解来构造参数矩阵[43]。此外,韩等 [44]通过计算Ricatti方程研究了Luenberger观测器网络中连续时间LTI系统的分布式观测器问题,并证明了联合可观测性是必要的。 2017 年,刘等 [45]研究了一类LTI系统的稳定性,并通过设计分布式观测器建立了复杂网络中协作控制的统一框架。随后,他们进一步探讨了LTI系统的分布式状态和扰动观测器的协作输出调节问题,并构建了网络观测器来观测系统状态,其中每个智能体仅获得部分输出测量[46]。
此外,最近关于MAS中分布式观测器设计的研究还考虑了更多约束,例如切换拓扑[47, 48]、外部干扰[49, 50]、状态全知[51]、同构[52, 53]、有限时间收敛[54, 55],以及现实世界系统需求中的一些特殊条件。对于离散 LTI 系统,分布式卡尔曼滤波器始终工作良好。然而,对于分布式观测器的设计,似乎是困难的。 2018 年,Mitra 等 [56]制定了部分状态而不是所有观测器状态的一致性。这是一种单时间尺度的策略,没有增强观测器可以更容易地更新观测器的状态。
LTI 系统的分布式观测器
在本节中,首先介绍图论[57]的一些预备知识。网络用 G = ( V , E ) G = (V, E) G=(V,E)表示,其中 V = 1 , 2 , ⋯ , N V = {1, 2,\cdots,N} V=1,2,⋯,N是节点的集合, E ∈ V × V i E\in V×V_i E∈V×Vi是边的集合。假设每条边都有一个关联的权值 w i j ∈ R + w_{ij} \in R^+ wij∈R+,网络 G G G的加权邻接矩阵 A = ( a i j ) A = (a_{ij}) A=(aij)定义为:如果 ( i , j ) ∈ E (i, j) \in E (i,j)∈E,则 a i j = w i j a_{ij} = w_{ij} aij=wij,否则 a i j = 0 a_{ij} = 0 aij=0。 矩阵 A 的拉普拉斯矩阵 L = L j i L =L_{ j i} L=Lji,由 L i i = ∑ j ≠ i a i j L_{ii} = \sum_{j \neq i} a_{ij} Lii=∑j=iaij和 L i j = − a i j , j ≠ i L_{ij} = −a_{ij},j \neq i Lij=−aij,j=i给出。如果对于每对不同的节点,都存在一条有向路径,则有向网络 G G G称为强连通。如果有一个节点存在到网络中任何其他节点的有向路径,则有向网络 G G G具有有向生成树。如果没有从 V / V s V/ V_s V/Vs到 V s V_s Vs的边,则网络 G G G的强连通分量 G ( V s , E s ) G(V_s, E_s) G(Vs,Es)是源分量。
离散LTI系统例子
在本小节中,我们回顾了近年来离散时间 LTI 系统的分布式观测器设计的几种典型方法。
{ x ( k + 1 ) = A x ( k ) , y i ( k ) = H i x ( k ) , i = 1 , 2 , … , N , \begin{cases}x(k+1)=Ax(k),\\y_i(k)=H_ix(k),&i=1,2,\ldots,N,&\end{cases} {x(k+1)=Ax(k),yi(k)=Hix(k),i=1,2,…,N,
y i ( k ) y_i(k) yi(k)是传感器 i 状态的测量, H i H_i Hi是输出矩阵,且 H = [ H 1 T , H 2 T , … , H N T ] T H=[H_1^\mathrm{T},H_2^\mathrm{T},\ldots,H_N^\mathrm{T}]^\mathrm{T} H=[H1T,H2T,…,HNT]T。观测器通过网络G=(V,E)与其他人进行交流。仅使用 x i ( k ) x_i(k) xi(k)及其邻居的信息来更新状态估计 x ^ i ( k ) \hat x_i(k) x^i(k)。观测器的内部状态由状态估计 x i ( k ) x_i(k) xi(k)和基于 y i ( k ) y_i(k) yi(k)更新的附加状态 z i ( k ) z_i(k) zi(k)组成。
定义 1. 考虑离散时间 LTI 系统 (1)。分布式观测器 x ^ i ( k ) \hat x_i(k) x^i(k)渐近达到全知,如果对于任何初始条件,每个观测器 x ^ i ( k ) \hat x_i(k) x^i(k)的状态都可以渐近收敛到 x ( k ) x(k) x(k),即
lim k → + ∞ ∥ x ^ i ( k ) − x ( k ) ∥ = 0 , i = 1 , 2 , … , N . \lim_{k\to+\infty}\|\hat{x}_i(k)-x(k)\|=0,~i=1,2,\ldots,N. k→+∞lim∥x^i(k)−x(k)∥=0, i=1,2,…,N.
为了实现上述目标,人们提出了多种设计分布式观测器的方法。其中一种典型的方法称为 DKF [58]。该方法提出了两步策略,一个是卡尔曼滤波器估计步骤,另一个是数据融合步骤。随后,DKF 的性能和稳定性在参考文献中进行了研究。 [59],导出了保证系统在所有本地观测器处渐近全知的充分必要条件。与参考文献不同。 [58],帕克等 [51]提出了一类在单一时间尺度上运行的分布式观测器。他们引入 z i ( k ) z_i(k) zi(k)作为观测器 i i i的增广态,并令 μ i \mu_i μi为 z i z_i zi的维数。然后,分布式观测器的可扩展性条件为
∑ i = 1 m μ i < m \sum_{i=1}^m\mu_i
其中 m m m是常数。
根据可扩展性条件(3),Park 等 [51]对状态全知的LTI系统采用参数化分布式观测器,其中对于任意 i ∈ V i\in V i∈V,观测器 i i i根据以下方程更新其内部状态:
{ x ^ i ( k + 1 ) = A ∑ j ∈ N i a i j x ^ j ( k ) + K i ( y i ( k ) − H i x ^ i ( k ) ) + P i z i ( k ) , z i ( k + 1 ) = Q i ( y i ( k ) − H i x ^ i ( k ) ) + S i z i ( k ) , \left.\left\{\begin{aligned}\hat{x}_i(k+1)&=A\sum_{j\in\mathbb{N}_i}a_{ij}\hat{x}_j(k)+K_i(y_i(k)-H_i\hat{x}_i(k))+P_{iz_i}(k),\\\\z_i(k+1)&=Q_i\left(y_i(k)-H_i\hat{x}_i(k)\right)+S_iz_i(k),\end{aligned}\right.\right. ⎩ ⎨ ⎧x^i(k+1)zi(k+1)=Aj∈Ni∑aijx^j(k)+Ki(yi(k)−Hix^i(k))+Pizi(k),=Qi(yi(k)−Hix^i(k))+Sizi(k),
其中 a i j ∈ R , K i ∈ R n × r i , P i ∈ R n × μ i , Q i ∈ R r i × μ i , S i ∈ R μ i × μ i \begin{aligned}a_{ij}\in\mathbb{R},K_i\in\mathbb{R}^{n\times r_i},P_i\in\mathbb{R}^{n\times\mu_i},Q_i\in\mathbb{R}^{r_i\times\mu_i},S_i\in\mathbb{R}^{\mu_i\times\mu_i}\end{aligned} aij∈R,Ki∈Rn×ri,Pi∈Rn×μi,Qi∈Rri×μi,Si∈Rμi×μi
是要设计的参数。 μ i \mu_i μi是增广态 z i z_i zi的维数。分布式观测器由增益矩阵确定 { K i , P i , Q i , S i } , i = 1 , 2 , … , N . \{K_i,P_i,Q_i,S_i\},i=1,2,\ldots,N. {Ki,Pi,Qi,Si},i=1,2,…,N.
注意,当且仅当系统(1)的状态可从与网络G的每个源组件相对应的组合输出部分检测到时,存在满足(3)的全知实现参数。如果这样的可检测性条件满足,则存在一个全知实现解,其所有增广状态的结果聚合维数都成立
∑ i = 1 m μ i ≤ m − m s \sum_{i=1}^m\mu_i\leq m-m_\text{s} i=1∑mμi≤m−ms
其中 m s m_s ms是源分量的数量。通过将网络 G G G划分为 m s m_s ms个源分量,证明了在可扩展性条件(5)下渐近实现全知的参数存在的充要条件。然后,他们的工作的主要定理如下。
定理 1. 考虑 LTI 系统 (1)。如果预先选择交互网络 G = ( V , E ) G=(V,E) G=(V,E),则可以得出以下结论[51]。
(1)网络G有m_s个源组件 { V l , E l } l = 1 m s {\{\mathcal{V}_l,\mathcal{E}_l\}}^{m_s}_{l=1} {Vl,El}l=1ms。每个源组件 ( { V l , E l ) (\{\mathcal{V}_l,\mathcal{E}_l) ({Vl,El)对应于 ( A , H V l ) (A,H_{\mathcal V_l}) (A,HVl)描述的LTI系统(1)的一个子系统。
(2) 对于每个 i ∈ V R i\in \mathcal V^R i∈VR, V R \mathcal V^R VR是源分量代表集。当且仅当所有子系统 { A , H V l } l = 1 m s {\{A,H_{\mathcal V_l}\}}^{m_s}_{l=1} {A,HVl}l=1ms均可检测时,系统(1)中存在式(5)形式的参数。
米特拉等 [56]提出了另一种有向强连通网络下LTI系统的分布式观测器设计方法。他们提出了一种分布式观测器,确保 LTI 系统状态、网络拓扑结构和测量结构的渐近重建。通过设计更新法则,节点可以根据自己的测量结果重建某些状态,成为一致性动态中的领导者。这种方法不仅产生了单时间尺度的算法,而且不需要任何状态增强,这可以简化观测器的设计。他们考虑了与每个源组件相关的子系统都是可检测的条件。他们工作的主要思想是通过一系列相似变换逐步进行可观察的规范分解,如下命题。
命题1.设A为系统矩阵, H 1 , H 2 , ⋯ , H N H_1,H_2,\cdots,H_N H1,H2,⋯,HN为观测矩阵族。定义 H = [ H 1 T , H 2 T , ⋯ , H N T ] T H = [H^T_1 , H^T_2 , \cdots,H^T_N]^T H=[H1T,H2T,⋯,HNT]T。然后有一个相似变换矩阵 T \mathcal T T,将 ( A , H ) (A, H) (A,H)变换为 ( A ˉ , H ˉ ) ( \bar A, \bar H) (Aˉ,Hˉ),使得 [56]
此外,对于 i = 1 , 2 , ⋯ , N , ( A i i , H i i ) i = 1, 2,\cdots,N,(A_{ii}, H_{ii}) i=1,2,⋯,N,(Aii,Hii)是可观测的, A U A_{\mathcal U} AU描述了不可观测子空间 ( A , C ) (A, C) (A,C)的动态。
让我们引入一个新的状态变量 z ( k ) z(k) z(k),它可以分为 N + 1 N + 1 N+1个部分,包括 N N N个子状态 z ( j ) ( k ) , j = 1 , 2 , ⋯ , N z^{(j)}(k),j = 1, 2,\cdots,N z(j)(k),j=1,2,⋯,N,和一个不可观察的子状态 z u ( k ) z_{\mathcal {u}}(k) zu(k)。根据命题 1,第 i 个子状态的动力学由下式给出
{ z ( i ) ( k + 1 ) = A i i z ( i ) ( k ) + ∑ j = 1 i − 1 A i j z ( j ) ( k ) y ( i ) ( k ) = H i i z ( i ) ( k ) + ∑ j = 1 i − 1 H i j z ( j ) ( k ) . \left\{\begin{array}{l} z^{(i)}(k+1)=A_{i i} z^{(i)}(k)+\sum_{j=1}^{i-1} A_{i j} z^{(j)}(k) \\ y^{(i)}(k)=H_{i i} z^{(i)}(k)+\sum_{j=1}^{i-1} H_{i j} z^{(j)}(k) . \end{array}\right. \\ {z(i)(k+1)=Aiiz(i)(k)+∑j=1i−1Aijz(j)(k)y(i)(k)=Hiiz(i)(k)+∑j=1i−1Hijz(j)(k).
值得注意的是,不可观测子状态 z u ( k ) z_{\mathcal u}(k) zu(k)的动力学由下式描述:
z u ( k + 1 ) = A u z u ( k ) + ∑ j = 1 N A j z ( j ) ( k ) z_u(k+1)=Auz_u(k)+\sum_{j=1}^NA_jz^{(j)}(k) zu(k+1)=Auzu(k)+j=1∑NAjz(j)(k)
定义 z ^ i ( j ) ( k ) \hat{z}^{( j)}_i (k) z^i(j)(k)为节点 i i i维护的第 j j j个子状态的估计。然后,用于更新子状态估计 z ^ i ( i ) ( k ) \hat{z}^{(i)}_i (k) z^i(i)(k)的 Luenberger 式观测器被提出为
z ^ i ( i ) ( k + 1 ) = A i i z ^ i ( i ) ( k ) + ∑ j = 1 i − 1 A i j z ^ i ( j ) ( k ) + L i ( y i ( k ) − ( H i i z ^ i ( i ) ( k ) + ∑ j = 1 i − 1 H i j z ^ i ( j ) ( k ) ) ) \begin{aligned} \hat{z}_i^{(i)}(k+1)& \begin{aligned}=A_{ii}\hat{z}_i^{(i)}(k)+\sum_{j=1}^{i-1}A_{ij}\hat{z}_i^{(j)}(k)\end{aligned} \\ &+L_i\left(y_i(k)-\left(H_{ii}\hat{z}_i^{(i)}(k)+\sum_{j=1}^{i-1}H_{ij}\hat{z}_i^{(j)}(k)\right)\right) \end{aligned} z^i(i)(k+1)=Aiiz^i(i)(k)+j=1∑i−1Aijz^i(j)(k)+Li(yi(k)−(Hiiz^i(i)(k)+j=1∑i−1Hijz^i(j)(k)))
其中 L i L_i Li是需要设计的增益矩阵。
为了估计第 j j j个子状态,基于一致性的方案用于更新所有其他子状态 z ^ i ( j ) ( k ) \hat{z}^{( j)}_i (k) z^i(j)(k)的构造如下:
z ^ i ( j ) ( k + 1 ) = A j j ∑ l ∈ N i w i l j z ^ l ( j ) ( k ) + ∑ l = 1 j − 1 A j l z ^ i ( l ) ( k ) \hat{z}_i^{(j)}(k+1)=A_{jj}\sum_{l\in\mathcal{N}_i}w_{il}^j\hat{z}_l^{(j)}(k)+\sum_{l=1}^{j-1}A_{jl}\hat{z}_i^{(l)}(k) z^i(j)(k+1)=Ajjl∈Ni∑wiljz^l(j)(k)+l=1∑j−1Ajlz^i(l)(k)
事实证明,如果与每个源组件相关的子系统都是可检测的,并且网络是强连通的,则增益矩阵 L i L_i Li和一致性权重 w i l j , j ≠ i , l ∈ N i {w^j_{il}, j \neq i, l \in \mathcal N_i} wilj,j=i,l∈Ni的存在可以用于通过等式(8)–(10)更新观测器。然后,他们的工作的主要定理如下。
定理2.假设网络 G G G是强连通的,有 m s m_s ms个源组件 { V l , E l } l = 1 m s {\{\mathcal{V}_l,\mathcal{E}_l\}}^{m_s}_{l=1} {Vl,El}l=1ms,并且所有子系统 { A , H V l } l = 1 m s {\{A,H_{\mathcal V_l}\}}^{m_s}_{l=1} {A,HVl}l=1ms都是可检测的。然后,通过等式(8)–(10)更新观测器,存在一组增益矩阵 L i L_i Li和一致性权重 w i l j , j ≠ i , l ∈ N i {w^j_{il}, j \neq i, l \in \mathcal N_i} wilj,j=i,l∈Ni[56]。
人们提出了许多其他高级研究来考虑更复杂的条件。例如,米特拉等 [60]提出了一种基于滑动窗口局部滤波的安全估计(SW-LFSE)算法来处理一类强( 2 f + 1 2f+1 2f+1)鲁棒网络,并分析了LTI网络系统中实现渐近稳定性的收敛速度。令 e i ( j ) ( k ) = z ^ i ( j ) ( k ) − z ( j ) ( k ) e_{i}^{(j)}(k)=\hat{z}_{i}^{(j)}(k)-z^{(j)}(k) ei(j)(k)=z^i(j)(k)−z(j)(k)为分量 z ( j ) ( k ) z^{(j)}(k) z(j)(k)的估计误差。对于所有 K ≥ ( T + 1 ) q K \ge (T + 1)q K≥(T+1)q,它满足
∣ e i ( j ) ( k ) ∣ ≤ β ( j ) [ ( N − ( 2 f + 1 ) ) ( ∣ λ j ∣ γ ( j ) ) ( T + 1 ) ] q ( γ ( j ) ) k \left|e_{i}^{(j)}(k)\right| \leq \beta^{(j)}\left[(N-(2 f+1))\left(\frac{\left|\lambda_{j}\right|}{\gamma^{(j)}}\right)^{(T+1)}\right]^{q}\left(\gamma^{(j)}\right)^{k} \\ ei(j)(k) ≤β(j)[(N−(2f+1))(γ(j)∣λj∣)(T+1)]q(γ(j))k
其中 β ( j ) > 0 \beta( j) > 0 β(j)>0和 γ ( j ) ∈ ( 0 , 1 ) \gamma( j) \in (0, 1) γ(j)∈(0,1)是一定的常数。值得注意的是,条件(11)导出了收敛误差的上限,它几乎可以同样地用于分析静态网络中有界通信延迟的影响。
此外,还研究了网络上的安全分布式状态估计问题,其中每个交互链路均由随机过程 ξ i j ( k ) \xi_{ij}(k) ξij(k)控制。对于交互网络 G G G,元素 a i j a_{ij} aij是概率为 p p p的伯努利丢包过程。给出了设计观测器保证均方稳定性的充分条件。
金等 [61]研究了LTI网络系统的加密分布式状态观测器设计问题,这意味着测量和状态估计的数据受到保护。所考虑的网络由本地观测器组成,其中每个观测器都使用加密的本地测量、加密的系统输入和加密的传输估计。分布式状态观测器设计为
{ z ^ i ( k + 1 ) = P i , i z ^ i ( k ) + Q i u ( k ) + R i y i ( k ) , w ^ i ( k + 1 ) = ∑ j ∈ N λ P i , j ξ ^ j ( k ) + Q i ′ u ( k ) , x ^ i ( k ) = S i ξ ^ i ( k ) , \left\{\begin{array}{l} \hat{z}_{i}(k+1)=P_{i, i} \hat{z}_{i}(k)+Q_{i} u(k)+R_{i} y_{i}(k), \\ \hat{w}_{i}(k+1)=\sum_{j \in \mathcal{N}_{\lambda}} P_{i, j} \hat{\xi}_{j}(k)+Q_{i}^{\prime} u(k), \\ \hat{x}_{i}(k)=S_{i} \hat{\xi}_{i}(k), \end{array}\right. \\ ⎩ ⎨ ⎧z^i(k+1)=Pi,iz^i(k)+Qiu(k)+Riyi(k),w^i(k+1)=∑j∈NλPi,jξ^j(k)+Qi′u(k),x^i(k)=Siξ^i(k),
其中 ξ ˉ i = c o l { z ˉ i , w ˉ i } \bar \xi_i = col\{ \bar z_i, \bar w_i\} ξˉi=col{zˉi,wˉi}。这里,第一个方程针对状态 x x x的可观测部分 ( A , H i ) (A,H_i) (A,Hi),第二个方程针对其余不可观测部分。所提出的分布式观测器中的观测器参数可以选择为整数,这不仅允许状态估计在有限时间内收敛,而且使加密的动态观测器在无限时间范围内运行。
备注 1. 上述在离散时间 LTI 系统中设计分布式观测器的方法是按时间顺序排列的。后来提出的每一种方法都是对前一种方法的改进或认为有更多的局限性。考虑的条件较多,计算量相对较少。例如,米特拉等 [56] 与 Park 等人相比,删除了状态增强。 [51],这简化了设计的计算。
连续时间 LTI 系统案例
我们将在本小节中概述过去五年中连续时间 LTI 系统的分布式观测器的设计。考虑连续时间 LTI 系统
{ x ˙ ( t ) = A x ( t ) , y i ( t ) = H i x ( t ) , i = 1 , 2 , … , N , \left\{\begin{array}{l} \dot{x}(t)=A x(t), \\ y_{i}(t)=H_{i} x(t), \quad i=1,2, \ldots, N, \end{array}\right. \\ {x˙(t)=Ax(t),yi(t)=Hix(t),i=1,2,…,N,
其中 x ( t ) ∈ R n x(t) \in \mathbb{ R}^n x(t)∈Rn是节点 i i i的状态, A ∈ R n × n A \in \mathbb{R}^{n \times n} A∈Rn×n是系统矩阵, y i ( t ) ∈ R r i y_i(t)\in \mathbb{R}^{r_i} yi(t)∈Rri是传感器 i 的状态测量, H i ∈ R r i × n H_i \in \mathbb{R}^{r_i \times n} Hi∈Rri×n是输出矩阵。观测器通过网络 G = ( V , E ) G = (V, E) G=(V,E)与其他人交互。仅使用 x i ( t ) x_i(t) xi(t)及其邻居的信息来更新状态估计 x ^ i ( t ) \hat{x}_i(t) x^i(t)。观测器的内部状态由状态估计 x i ( t ) x_i(t) xi(t)和基于 y i ( t ) y_i(t) yi(t)更新的附加状态 z i ( t ) z_i(t) zi(t)组成。
定义 2. 考虑状态为 x ( t ) x(t) x(t)的连续时间 LTI 系统 (13),如果对于任何初始条件,分布式观测器 x ^ i ( t ) \hat{x}_i(t) x^i(t)渐近地达到全知,并且每个观测器的状态渐近收敛于 x ( t ) x(t) x(t)。那是,
lim t → + ∞ ∥ x ^ i ( t ) − x ( t ) ∥ = 0 , i = 1 , 2 , … , N . \lim_{t \rightarrow+\infty}\left\|\hat{x}_{i}(t)-x(t)\right\|=0, \quad i=1,2, \ldots, N . \\ t→+∞lim∥x^i(t)−x(t)∥=0,i=1,2,…,N.
参考文献[62]指出,在某些方面,连续时间LTI系统的分布式观测器的设计(13)类似于领导者跟随一致性协议的设计。如果系统中节点 0 的状态为零控制,并且通信网络包含一棵以节点 0 为根的生成树,则分布式观测器的设计将类似于与领导者达成一致性的协议设计。它运作良好,因为协议设计仅依赖于分布式观测器设计中可以获得的邻居信息。因此,我们首先回顾一下 LTI MAS 的领导者跟随一致性问题。每个智能体的动态描述为
x ˙ i ( t ) = A x i ( t ) + B u i ( t ) , i = 0 , 1 , … , N , \dot{x}_i(t)=Ax_i(t)+Bu_i(t),~i=0,1,\ldots,N, x˙i(t)=Axi(t)+Bui(t), i=0,1,…,N,
为了解决这个问题。李等 [41] 提出了一种完全分布式自适应一致性协议,这是由于有向网络下的零输入领导者的相邻信息的相对状态。分布式自适应一致性协议的构建如下:
{ u i ( t ) = c i ( t ) ρ i ( ξ i T ( t ) P − 1 ξ i ( t ) ) K ξ i ( t ) , c ˙ i ( t ) = ξ i T ( t ) Γ ξ i ( t ) , \left\{\begin{array}{l} u_{i}(t)=c_{i}(t) \rho_{i}\left(\xi_{i}^{\mathrm{T}}(t) P^{-1} \xi_{i}(t)\right) K \xi_{i}(t), \\ \dot{c}_{i}(t)=\xi_{i}^{\mathrm{T}}(t) \Gamma \xi_{i}(t), \end{array}\right. {ui(t)=ci(t)ρi(ξiT(t)P−1ξi(t))Kξi(t),c˙i(t)=ξiT(t)Γξi(t),
其中 ξ i = ∑ j = 0 N a i j ( x i ( t ) − x j ( t ) ) , c i ( t ) \xi_{i}=\sum_{j=0}^{N} a_{i j}\left(x_{i}(t)-x_{j}(t)\right), c_{i}(t) ξi=∑j=0Naij(xi(t)−xj(t)),ci(t)为跟随者 i i i对应的时变耦合权重, c i ( 0 ) > 1 , K ∈ R p × n c_i(0) > 1,K \in \mathbb{R}^{p\times n} ci(0)>1,K∈Rp×n和 Γ ∈ R n × n \Gamma \in \mathbb{R}^{n\times n} Γ∈Rn×n为待确定的反馈增益矩阵。通过求解线性矩阵不等式 A P + P A T − 2 B B T < 0 AP + PA^T − 2BB^T < 0 AP+PAT−2BBT<0得到 P > 0 P > 0 P>0。根据以下定理推导出构建自适应一致性协议(16)的充分条件。
定理3.假设交互网络G有一棵以Leader为根节点的生成树。然后,MAS (15) 的领导者跟随一致性问题通过分布式自适应协议 (16) 解决,其中 K = − B T P − 1 , Γ = P − 1 B B T P − 1 K = −B^TP^{−1}, \Gamma= P^{−1}BB^TP^{−1} K=−BTP−1,Γ=P−1BBTP−1,并且$\rho_{i}\left(\xi_{i}^{\mathrm{T}} P^{-1} \xi_{i}\right)=\left(1+\xi_{i}^{\mathrm{T}} P^{-1} \xi_{i}\right)^{3} ,其中 ,其中 ,其中P 是 是 是AP + PA^T − 2BB^T < 0$ 的解[41]。
对于具有非零输入领导者的 MAS (15),Lv 等 [63]通过开发一种新颖的自适应协议解决了完全分布式一致性问题。基于对相邻智能体状态的相对估计,他们向每个跟随者提出了分布式连续自适应控制器,如下所示:
{ v ˙ i = A v i + B u i + F ( H v i − y i ) , w ˙ i = A w i + ( d i + ρ i ) F H ψ i − β B h i ( B T Q ψ i ) , u i = K ( v i − w i ) − β g i ( B T Q η i ) , v ˙ i = − φ i ( d i − 1 ) + ψ i T H T H ψ i , \left\{\begin{array}{l} \dot{v}_{i}=A v_{i}+B u_{i}+F\left(H v_{i}-y_{i}\right), \\ \dot{w}_{i}=A w_{i}+\left(d_{i}+\rho_{i}\right) F H \psi_{i}-\beta B h_{i}\left(B^{\mathrm{T}} Q \psi_{i}\right), \\ u_{i}=K\left(v_{i}-w_{i}\right)-\beta g_{i}\left(B^{\mathrm{T}} Q \eta_{i}\right), \\ \dot{v}_{i}=-\varphi_{i}\left(d_{i}-1\right)+\psi_{i}^{\mathrm{T}} H^{\mathrm{T}} H \psi_{i}, \end{array}\right. \\ ⎩ ⎨ ⎧v˙i=Avi+Bui+F(Hvi−yi),w˙i=Awi+(di+ρi)FHψi−βBhi(BTQψi),ui=K(vi−wi)−βgi(BTQηi),v˙i=−φi(di−1)+ψiTHTHψi,
其中 v i ∈ R v_i \in \mathbb R vi∈R是跟随者 i 的状态估计,
ψ i = ∑ j = 0 N a i j ( w i − w j ) , η i = ∑ j = 0 N a i j ( v i − v j ) , ρ i = ψ i T S ψ i , \psi_{i}=\sum_{j=0}^{N} a_{i j}\left(w_{i}-w_{j}\right), \eta_{i}=\sum_{j=0}^{N} a_{i j}\left(v_{i}-v_{j}\right), \rho_{i}=\psi_{i}^{\mathrm{T}} S \psi_{i} \text {, } ψi=∑j=0Naij(wi−wj),ηi=∑j=0Naij(vi−vj),ρi=ψiTSψi,
S > 0 、 Q > 0 、 β > 0 S > 0、Q > 0、\beta>0 S>0、Q>0、β>0为正常数, g i g_i gi为非线性函数 d i d_i di为时变耦合权重, φ i \varphi_i φi为小正常数。
对于连续 LTI MAS 的分布式观测器设计问题
{ x ˙ ( t ) = A x ( t ) + ∑ i = 1 N B i u i ( t ) , y i ( t ) = C i x ( t ) , i = 1 , 2 , … , N . \left\{\begin{array}{l} \dot{x}(t)=A x(t)+\sum_{i=1}^{N} B_{i} u_{i}(t), \\ y_{i}(t)=C_{i} x(t), \quad i=1,2, \ldots, N . \end{array}\right. \\ {x˙(t)=Ax(t)+∑i=1NBiui(t),yi(t)=Cix(t),i=1,2,…,N.
刘等 [45]根据网络观测器建立了合作稳定的统一框架。与传统的集中式设计不同,他们提出了一种仅使用网络系统本地信息的协作方法。具体来说,观测器 i i i仅获得输出信息 y i ( t ) y_i(t) yi(t),观测器设计为
x ^ ˙ i ( t ) = A x ^ i ( t ) + M i ( y i ( t ) − H i x ^ i ( t ) ) − v ∑ j = 1 N a i j ( t ) ( x ^ i ( t ) − x ^ j ( t ) ) + φ i B i u i ( t ) , \dot{\hat{x}}_{i}(t)=A \hat{x}_{i}(t)+M_{i}\left(y_{i}(t)-H_{i} \hat{x}_{i}(t)\right) \\ -v \sum_{j=1}^{N} a_{i j}(t)\left(\hat{x}_{i}(t)-\hat{x}_{j}(t)\right)+\varphi_{i} B_{i} u_{i}(t), x^˙i(t)=Ax^i(t)+Mi(yi(t)−Hix^i(t))−vj=1∑Naij(t)(x^i(t)−x^j(t))+φiBiui(t),
其中控制输出由下式给出
u i = K i x ^ i , i = 1 , 2 , … , N u_{i}=K_{i} \hat{x}_{i}, \quad i=1,2, \ldots, N \\ ui=Kix^i,i=1,2,…,N
其中矩阵 M i M_i Mi和 K i K_i Ki是待确定的反馈增益, ν ν ν是耦合强度。推导了强连通网络、生成树有向网络和交换网络三种网络拓扑下确保MAS稳定的一些充分条件。以下定理给出了强连通网络中的主要结果,其他情况与强连通网络类似。
定理 4. 对于强连通网络中的分布式观测器 (19),存在参数 ν ν ν、 K i K_i Ki、 H i H_i Hi和 φ i \varphi_i φi,使得 LTI MAS (18) 稳定,当且仅当 ( A , H ) (A, H) (A,H)可检测时, A − ∑ i = 1 N H ^ i C i A-\sum_{i=1}^{N} \hat{H}_{i} C_{i} A−∑i=1NH^iCi和 A + ∑ i = 1 N B i K ^ i A+\sum_{i=1}^{N} B_{i} \hat{K}_{i} A+∑i=1NBiK^i是 Hurwitz [45]。
与 Mitra 等人的案例类似。 [56]关于离散时间LTI系统,连续时间LTI系统中可观测正则分解的思想仍然有效。金等 [43]通过采用智能体可检测性分解,提出了连续时间 LTI 系统的分布式状态观测器的分散设计。在这里,我们回顾一下正交变换,它为 ( A , H i ) (A, H_i) (A,Hi)的不可检测子空间产生可检测性分解。与卡尔曼可观性分解类似,如果存在正交变换矩阵 T i = [ D i , U i ] T_i=[D_i,U_i] Ti=[Di,Ui],则矩阵 ( A i d , H i d ) (A_{id},H_{id}) (Aid,Hid)是可检测的,而矩阵 A i u A_{iu} Aiu是不稳定的。那么矩阵 A A A和 H i H_i Hi可以变换为以下形式:
T i T A T i = [ A i d 0 A i r A i u ] , H i T i = [ H i d 0 ] . T_{i}^{\mathrm{T}} A T_{i}= {\left[\begin{array}{cc} A_{i d} & 0 \\ A_{i r} & A_{i u} \end{array}\right], \quad H_{i} T_{i}=\left[H_{i d} 0\right] . } TiTATi=[AidAir0Aiu],HiTi=[Hid0].
根据上述分析,为了推导有向网络底层观测器存在的充要条件,系统(18)的分布式观测器设计如下:
x ^ ˙ i ( t ) = A x ^ i ( t ) + L i ( y i ( t ) − H i x ^ i ( t ) ) + γ i M i ∑ j ∈ N i α i j ( x ^ j ( t ) − x ^ i ( t ) ) \dot{\hat{x}}_{i}(t)= A \hat{x}_{i}(t)+L_{i}\left(y_{i}(t)-H_{i} \hat{x}_{i}(t)\right) \\ +\gamma_{i} M_{i} \sum_{j \in \mathcal{N}_{i}} \alpha_{i j}\left(\hat{x}_{j}(t)-\hat{x}_{i}(t)\right) x^˙i(t)=Ax^i(t)+Li(yi(t)−Hix^i(t))+γiMij∈Ni∑αij(x^j(t)−x^i(t))
其中 L i L_i Li是注入增益矩阵, M i M_i Mi是加权矩阵, γ i \gamma_i γi是耦合增益。矩阵 L i L_i Li和 M i M_i Mi构造为
L i = T i [ L i d 0 ] , M i = T i [ 0 0 0 I v i ] T i T . L_{i}= T_{i}\left[\begin{array}{c} L_{i d} \\ 0 \end{array}\right], \quad M_{i}=T_{i}\left[\begin{array}{cc} 0 & 0 \\ 0 & I_{v_{i}} \end{array}\right] T_{i}^{\mathrm{T}} . Li=Ti[Lid0],Mi=Ti[000Ivi]TiT.
定理5.假设 ( A , H ) (A,H) (A,H)是可检测的并且所考虑的网络 G G G是有向强连通的。那么所提出的分布式观测器(21)的LTI耦合增益 γ i \gamma_i γi满足[43]
γ i > 2 ( max i ∈ N { ∥ A i u ∥ } + β ) λ min ( U T ( L ^ ( G ) ⊗ I n ) U ) , ∀ i ∈ N \gamma_{i}> \frac{2\left(\max _{i \in \mathcal{N}}\left\{\left\|A_{i u}\right\|\right\}+\beta\right)}{\lambda_{\min }\left(U^{\mathrm{T}}\left(\hat{\mathcal{L}}(G) \otimes I_{n}\right) U\right)}, \quad \forall i \in \mathcal{N} γi>λmin(UT(L^(G)⊗In)U)2(maxi∈N{∥Aiu∥}+β),∀i∈N
针对连续时间 LTI MAS 的分布式观测器的设计,人们还进行了许多其他高级研究。例如,刘等 [64]提出了一种针对任意大交互延迟的分布式观测器的设计方法。与传统的集中式观测器能够获得系统的全部输出信息不同,这些观测器只需要分布式传感器网络底层每个智能体的部分输出信息。他们考虑了三种代表性的网络拓扑,包括无向连通网络、有向强连通网络和包含生成树的有向网络,并建立了一些条件来确保观测误差系统能够分别在每种拓扑下实现指数稳定性。在存在时间延迟的情况下,观测器可以设计为
x ^ ˙ i ( t ) = A x ^ i ( t ) − ∑ j = 1 N a i j M ( x ^ i ( t − τ 1 ) − x ^ j ( t − τ 1 ) ) + G i ( y i ( t − τ 2 ) − H i e − A τ 2 x ^ i ( t ) ) \dot{\hat{x}}_{i}(t)= A \hat{x}_{i}(t)-\sum_{j=1}^{N} a_{i j} M\left(\hat{x}_{i}\left(t-\tau_{1}\right)-\hat{x}_{j}\left(t-\tau_{1}\right)\right) +G_{i}\left(y_{i}\left(t-\tau_{2}\right)-H_{i} e^{-A \tau_{2}} \hat{x}_{i}(t)\right) x^˙i(t)=Ax^i(t)−j=1∑NaijM(x^i(t−τ1)−x^j(t−τ1))+Gi(yi(t−τ2)−Hie−Aτ2x^i(t))
其中时间延迟 τ 1 \tau_1 τ1和 τ 2 \tau_2 τ2是常数。
此外,韩等 [44]提出了一种简单的方法来设计连续时间 LTI MAS 的分布式观测器。与 Kim 等人的方法相比。在参考文献中提出。 [43],这种方法要求局部观测器之间的输出信息通过有向强连通网络进行交互,并且每个智能体处的局部Luenberger观测器与被观察系统具有相同的阶数。 LTI 系统 (13) 的分布式 Luenberger 观测器设计为
x ^ ˙ i ( t ) = A x ^ i ( t ) + L i ( y i ( t ) − H i x ^ i ( t ) ) + γ M i ∑ j = 1 N a i j ( x ^ j ( t ) − x ^ i ( t ) ) \dot{\hat{x}}_{i}(t)= A \hat{x}_{i}(t)+L_{i}\left(y_{i}(t)-H_{i} \hat{x}_{i}(t)\right) +\gamma M_{i} \sum_{j=1}^{N} a_{i j}\left(\hat{x}_{j}(t)-\hat{x}_{i}(t)\right) x^˙i(t)=Ax^i(t)+Li(yi(t)−Hix^i(t))+γMij=1∑Naij(x^j(t)−x^i(t))
指出如果被观测的LTI系统(13)是可观测的并且网络拓扑是强连通的,则可以设计分布式观测器(24)。此外,可以使估计误差在至少 α > 0 \alpha>0 α>0的任何给定衰减率下收敛到零。
备注2.由于连续时间LTI系统中的分布式观测器设计没有统一的框架,上述这些方法考虑了许多不同的方面,例如可观测性分解、自适应方法和有限时间收敛。受到 Mitra 等人的工作的启发。 [56],奥尔特加等 [65]采用基于参数估计的方法来设计具有有限收敛时间的分布式观测器。与离散时间情况不同,通过求解矩阵方程可以清楚地看出如何设计观测器。
分布式观测器设计的前景
“需求拉动、技术推动”是人类文明进步的不竭动力。分布式观测器技术的广泛应用将为社会生产和生活方式带来深刻变革。展望新时代智能控制技术分布式观测器设计的发展,重塑我们面临的机遇和挑战。在最后几节中,我们只回顾了离散时间和连续时间 LTI 系统的几种典型的简单分布式观测器设计方法。在现实的工程系统中,存在许多影响系统性能的约束,包括时变、非线性、有限时间收敛、执行器饱和和随机扰动等。为了使模型更加实用,在分布式观测器的设计中应该考虑这些约束。
在现实系统中,系统参数和模型结构会随着时间的演化而变化。因此,时变系统的分布式观测器的设计值得探索。 2020 年,蔡等 [62]考虑了领导者跟随时变MAS的分布式输出观测器设计问题。为了解决这个问题,他们提出了一种自适应分布式输出观测器,它只依赖于领导者系统的输出信息,比基于状态的自适应分布式观测器更加实际。这种方法足以估计系统矩阵的最小多项式的系数,而不是系统矩阵的所有条目,这可以减少观测器的维度以及智能体之间的信息交互。
为了节省成本和提高效率,有限时间观测器的设计是另一个值得研究的重要问题。 2020 年,奥尔特加等 [65]采用基于参数估计的方法来设计具有有限收敛时间的分布式观测器。他们通过使用可观测性分解引入了一种基于参数估计的通用观测器方法。观测器的结构是通过封闭哈密顿游走设计的。在每次行走中,观测者估计只需要有限时间内MAS的部分状态信息。所提出的方法被认为是鲁棒的外部干扰和交互延迟。
此外,非线性是系统控制的关键问题。对于一类非线性 MAS,Xu 等 [66]针对这种情况处理了分布式观测器的方案。为了克服非线性,引入部分可观测规范形式(POCF)来设计局部观测器。由于POCF中的输出信息不同,所有本地观测器的结构也不同。推导了几个充分条件,以确保所提出的分布式观测器能够渐近地达到全知。
通过对分布式观测器设计的研究和分析发现,虽然已经提出了许多有效的方法来解决各种问题,但仍然存在许多缺点需要克服。将工程领域的新技术、新方法引入分布式观测器设计的研究中,对于提高控制系统的性能具有重要作用。
结论
本文介绍了 LTI 系统中分布式观测器设计的代表性模型和相关方法。首先,我们简要回顾了分布式观测器设计的研究背景和主要进展。此外,我们还分别详细介绍了离散时间和连续时间 LTI MAS 分布式观测器设计的一些最新成果。最后,我们对分布式观测器的设计提出了几点展望和未来的工作方向。仍然有许多缺点需要克服,我们相信由于技术的进步,将会提出许多分布式观测器设计的方法。