【数据结构X.6】代码实现：左孩子右兄弟表示法转换为树的双亲表示法，左孩子右兄弟表示法转化为树的孩子兄弟链表表示法，树的双亲表示法转化为左孩子右兄弟的二叉树表示法

前文提要:

【数据结构】树、森林的双亲表示法，左孩子右兄弟表示法，创建树的左孩子右兄弟二叉树以及二叉树到树的双亲表示法的转换思路和算法

本文主题：

可执行代码和代码示例在最后。

1. 【左孩子右兄弟】表示法转换为树的【双亲表示法】
2. 【左孩子右兄弟】表示法转化为树的【孩子兄弟】链表表示法
3. 树的【双亲表示法】转化为【左孩子右兄弟】的二叉树表示法

其他的例如【孩子兄弟】链表表示法转【左孩子右兄弟】的二叉树表示法，【孩子兄弟】链表表示法转【双亲表示法】，都是类似的原理，不再赘述了。

正文：

1.【左孩子右兄弟】表示法转化为树的【双亲表示法】链表表示法

算法描述:

如果树有左孩子，那么左孩子的父节点就是双亲节点
如果树有右孩子，那么说明树的父节点也是右孩子父节点
最好用中序遍历二叉树，这样会先遍历全部的孩子节点

函数：

void TransChildBrother2PrentArray(ForestHead fr, ForestArray *farray);
void GetParentArrayTreeList(ForestHead fr, ForestArray *farray, int nodeNum);

求解过程详细图解:

该博客的末尾部分进行了详细说明

主要思路是：

1.有孩子信息的可以直接建立孩子父亲关系。
2.兄弟信息需要去查找先序兄弟的父亲，从而建立孩子父亲关系；

---

2.左孩子右兄弟】表示法转化为树的【孩子兄弟】链表表示法

算法描述:

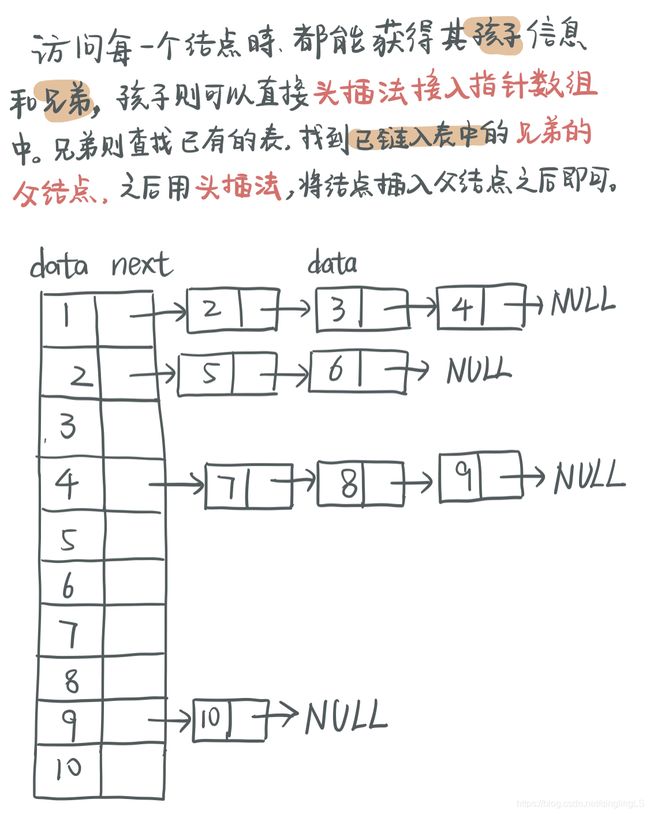
 每一个有孩子的节点，都需要在数组中一个保存位置,
 而且对于每个叶子节点，需要知道该节点的父亲,
 前序遍历，并且一边遍历一遍用头插法插入孩子和兄弟节点

函数：

ChildNode *FindFatherNode(ChildTree *rt, int x);//查找某个兄弟x的兄弟的父亲节点
ChildTree *TransChildBrother2ChildTree(ForestHead tr);

求解过程详细图解:

---

3.树的【双亲表示法】转化为【左孩子右兄弟】的二叉树表示法

算法描述:

树的双亲表示法转化为 左孩子右兄弟的二叉树表示法
 
 1.先把父子关系，转化为父子兄弟关系
 2.先找孩子节点，再找兄弟节点，rt里存了孩子信息，rtBrother里存了兄弟信息
 由于树的根节点的顺序存在表里，没有特别用一个index标记子节点的顺序，所以顺序被打乱了，
 不按照index存储双亲节点，将会出现孩子顺序乱序的情况，
 改起来太麻烦了，总体树的形状是没有改变的，
 如果是按照index的顺序存表，那么结果依然是顺序的

函数：

int FindForestArrayNextBrother(ForestArray *rt, int nodeNum, int x);//查找节点x的下一个兄弟的坐标
int FindForestArrayChild(ForestArray *rt, int nodeNum, int x);//查找节点x的第一个孩子的坐标
ForestHead TransParent2ChildBrother(ForestArray *rt, int nodeNum);

求解过程详细图解:

利用函数，查找每个节点的兄弟和孩子节点，
然后顺着树的前序序列，插入到树的节点中；

主要思路是：

1.查找每个节点的第一个孩子节点和下一个兄弟节点
2.在适当的时候，插入孩子节点和兄弟节点，所谓的适当的时候，就是当指针访问孩子节点和兄弟节点时。

---

函数实现：

Trees.h

#include 
#define MAX_SIZE 50
#include 
#include 
#include 
typedef struct ForestNode
{
    int data;
    struct ForestNode *lchild, *rbrother;
} ForestNode, *ForestHead;

/***
 * 树的前序遍历建立树，可见访问顺序相当于二叉树的中序遍历
 */
ForestHead CreateForestHead(ForestHead fr, bool isRoot)
{
    if (isRoot)
        std::cout << "请输入第一棵树根节点,-1标识空:";
    int data;
    fr = (ForestNode *)malloc(sizeof(ForestNode));
    std::cin >> data;
    fr->lchild = NULL;
    fr->rbrother = NULL;
    fr->data = data;
    if (data != -1)
    {
        bool isRoot = false;
        std::cout << "请输入" << data << "的首个孩子:";
        fr->lchild = CreateForestHead(fr->lchild, isRoot);
        std::cout << "请输入" << data << "的相邻兄弟:";
        fr->rbrother = CreateForestHead(fr->rbrother, isRoot);
    }
    return fr;
}

/***
 * 双亲表示法
 */
typedef struct TreeNode
{
    int valid = 0;  //该节点是否存储了父节点信息，如果没有，那么只是跳转指针,存储的是兄弟信息
    int parent = 0; //-1表示无父节点，其他表示指向的父节点
} TreeNode;

typedef struct ForestArray
{
    TreeNode f[MAX_SIZE];
} ForestArray; //森林的数列定义

/***
 * 将左孩子，右兄弟的存储方式的树，转化为双亲表示法
 */
void TransChildBrother2PrentArray(ForestHead fr, ForestArray *farray)
{
    if (fr)
    {
        TransChildBrother2PrentArray(fr->lchild, farray);
        if (fr->data != -1)
        {
            //std::cout << fr->data << "\t左孩子：" << fr->lchild->data << "\t右兄弟： " << fr->rbrother->data << std::endl;
            if (fr->rbrother->data != -1) //有了兄弟,记录类型为指针，指向第一个兄弟，
            {
                farray->f[fr->rbrother->data].valid = 0;
                farray->f[fr->rbrother->data].parent = fr->data;
            }
            if (fr->lchild->data != -1) //有了孩子，记录类型为真实值，孩子的parent置为父亲值
            {
                farray->f[fr->lchild->data].valid = 1;
                farray->f[fr->lchild->data].parent = fr->data;
            }
        }
        TransChildBrother2PrentArray(fr->rbrother, farray);
    }
}

/***
 * 把树的左孩子右兄弟表示法转换为双亲表示法
 * 
 * 如果树有左孩子，那么左孩子的父节点就是双亲节点
 * 如果树有右孩子，那么说明树的父节点也是右孩子父节点
 * 最好用中序遍历二叉树，这样会先遍历全部的孩子节点
 * 
 * 中序遍历：5 6 2 3 7 8 10 9 4 1
 * 
 */
void GetParentArrayTreeList(ForestHead fr, ForestArray *farray, int nodeNum)
{
    TransChildBrother2PrentArray(fr, farray); //将左孩子，右兄弟的存储方式的树，转化为双亲表示法
    std::cout << "将左孩子，右兄弟的存储方式的树，转化为双亲表示法:\n";
    for (int i = 1; i <= nodeNum; i++)
    {
        if (farray->f[i].valid != 0 && farray->f[i].valid != 1) //进行迭代，如果是树的根节点，有效位和双亲标志-1
        {
            farray->f[i].valid = -1;
            farray->f[i].parent = -1;
        }
        while (farray->f[i].valid == 0) //当有效位为0时，根据兄弟节点，去查找父亲节点值，直到找到为止。
        {
            if (farray->f[farray->f[i].parent].valid == 1)
                farray->f[i].valid = 1;
            farray->f[i].parent = farray->f[farray->f[i].parent].parent;
        }
        std::cout << "数据" << i << "指向：\t" << farray->f[i].parent << "\t是否指向父节点： " << farray->f[i].valid << std::endl;
    }
}

/***
 * 树的孩子表示法
 */
typedef struct ChildNode //根节点
{
    int parentId;            //指向自身，表示无孩子节点，否则是叶节点，则指向父节点
    struct ChildNode *child; //指向孩子节点
} RootNode, ChildNode;

typedef struct ChildTree
{
    RootNode parents[MAX_SIZE];
} ChildTree;

/***
 * 查找某个兄弟x的兄弟的父亲节点
 */
ChildNode *FindFatherNode(ChildTree *rt, int x)
{
    for (int i = 0; i < MAX_SIZE; i++)
    {
        ChildNode *p = rt->parents[i].child;
        while (p != NULL)
        {
            if (x != p->parentId)
                p = p->child;
            else
            {
                return rt->parents[i].child;
            }
        }
    }
    return NULL;
}
/***
 * 左孩子右兄弟表示法转化为树的孩子兄弟链表表示法
 * 
 * 每一个有孩子的节点，都需要在数组中一个保存位置,
 * 而且对于每个叶子节点，需要知道该节点的父亲
 * 前序遍历序列:1 2 5 6 3 4 7 8 9 10
 * 前序遍历，并且一边遍历一遍插入孩子和兄弟节点
 */
ChildTree *TransChildBrother2ChildTree(ForestHead tr)
{

    std::cout << "前序遍历【左孩子右兄弟】表示法转化为【孩子兄弟】链表表示法：";
    ChildTree *child = (ChildTree *)malloc(sizeof(ChildTree));
    for (int i = 0; i < MAX_SIZE; i++) //初始化根节点数组,数据都存为0，空指针
    {
        child->parents[i].child = NULL;
        child->parents[i].parentId = 0;
    }

    std::stack<ForestNode *> s, roots;
    ForestNode *p = tr;
    while (p || !s.empty())
    {
        //std::cout << p->data << " ";
        if (p)
        {
            if (p->data != -1)
            {
                std::cout << p->data << " ";
                if (p->lchild && p->lchild->data != -1) //左节点非空，且不是-1，有孩子，链接父子关系
                {
                    child->parents[p->data].parentId = p->data;
                    child->parents[p->lchild->data].parentId = p->data;
                    ChildNode *tmp = child->parents[p->data].child;
                    ChildNode *node = (ChildNode *)malloc(sizeof(ChildNode)); //新建节点，头插法放入节点中
                    node->parentId = p->lchild->data;
                    child->parents[p->data].child = node;
                    node->child = tmp;
                }
                if (p->rbrother && p->rbrother->data != -1)
                {
                    RootNode *father = FindFatherNode(child, p->data); //找到了兄弟的父亲节点，把兄弟也插入进父亲节点的后面
                    child->parents[p->rbrother->data].parentId = father->parentId;
                    ChildNode *node = (ChildNode *)malloc(sizeof(ChildNode)); //新建节点，头插法放入节点中
                    node->parentId = p->rbrother->data;
                    ChildNode *tmp = father->child;
                    father->child = node;
                    node->child = tmp;
                }
            }

            s.push(p);
            p = p->lchild;
        }
        else
        {
            p = s.top();
            s.pop();
            p = p->rbrother;
        }
    }
    return child;
}

/**
 * 访问孩子表示法的节点，打印
 */
void VisitByChildTree(ChildTree *rt, int nodeNum)
{
    std::cout << "\n访问孩子链表表示法的节点：";
    for (int i = 1; i <= nodeNum; i++)
    {
        ChildNode *p = rt->parents[i].child;

        std::cout << std::endl;
        std::cout << i << " | " << i;
        while (p != NULL)
        {
            std::cout << " -> " << p->parentId;
            p = p->child;
        }
    }
    std::cout << std::endl;
}

/***
 * 双亲表示法访问树节点：
 */
void VisitByParentArray(ForestArray *farray, int nodeNum)
{
    std::cout << "\n双亲表示法访问树节点：\n";
    for (int i = 1; i <= nodeNum; i++)
    {
        std::cout << "数据" << i << "指向：\t" << farray->f[i].parent << "\t是否指向父节点： " << farray->f[i].valid << std::endl;
    }
}

/**
 * 查找节点x的下一个兄弟的坐标
 */
int FindForestArrayNextBrother(ForestArray *rt, int nodeNum, int x)
{
    if (rt->f[x].valid == -1)
        return -1; //是根节点，无兄弟可返回
    for (int i = x + 1; i <= nodeNum; i++)
    {
        if (rt->f[i].parent == rt->f[x].parent)
        {
            return i; //返回下一个兄第
        }
    }
    return -1; //没有下一个兄弟了，是最小的孩子
}

/**
 * 查找节点x的第一个孩子的坐标
 */
int FindForestArrayChild(ForestArray *rt, int nodeNum, int x)
{
    for (int i = 1; i <= nodeNum; i++)
    {
        if (rt->f[i].parent == x)
            return i;
    }
    return -1;
}

/***
 * 树的双亲表示法转化为 左孩子右兄弟的二叉树表示法
 * 
 * 1.先把父子关系，转化为父子兄弟关系
 * 2.先找孩子节点，再找兄弟节点，rt里存了孩子信息，rtBrother里存了兄弟信息
 * 由于树的根节点的顺序存在表里，没有特别用一个index标记子节点的顺序，所以顺序被打乱了，
 * 不按照index存储双亲节点，将会出现孩子顺序乱序的情况，
 * 改起来太麻烦了，总体树的形状是没有改变的，
 * 如果是按照index的顺序存表，那么结果依然是顺序的
 */
ForestHead TransParent2ChildBrother(ForestArray *rt, int nodeNum)
{
    //1.先把父子关系，转化为父子兄弟关系
    int father = 1;
    ForestArray *rtBrother = (ForestArray *)malloc(sizeof(ForestArray)); //保存兄弟坐标
    memset(rtBrother, 0, sizeof(ForestArray));
    while (rt->f[father].parent != -1) //没父亲的时候找下一个节点
        father += 1;                   //找到树的根节点，其父亲节点的为-1
    for (int i = 1; i <= nodeNum; i++)
    {
        int nextBrother = FindForestArrayNextBrother(rt, nodeNum, i);
        if (nextBrother != -1)
        {
            rtBrother->f[i].parent = nextBrother;
            rtBrother->f[i].valid = 1;
        }
    }
   // VisitByParentArray(rt, nodeNum);
    //VisitByParentArray(rtBrother, nodeNum);
    //2.先找孩子节点，再找兄弟节点，rt里存了孩子信息，rtBrother里存了兄弟信息
    
    ForestHead ft = (ForestNode *)malloc(sizeof(ForestNode));
    ForestHead ftRoot =ft;
    ft->data = father; //双亲表示法根节点一定在第一个
    std::stack<ForestNode *> s;
    while (ft || !s.empty())
    {
        if (ft)
        {
            s.push(ft);
            int child = FindForestArrayChild(rt, nodeNum, father);
            //std::cout << "father: " << father << " child: " << child << std::endl;
            if (child != -1)
            {
                ft->lchild = (ForestNode *)malloc(sizeof(ForestNode));
                ft->lchild->data = child;
                father = child;
            }
            else
            {
                ft->lchild = NULL;
            }
            ft = ft->lchild;
        }
        else
        {
            ft = s.top();
            father = ft->data;
            s.pop();
            int brother = FindForestArrayNextBrother(rt, nodeNum, father);
            //std::cout << "father: " << father << " brother: " << brother << std::endl;
            if (brother != -1)
            {
                ft->rbrother = (ForestNode *)malloc(sizeof(ForestNode));
                ft->rbrother->data = brother;
                father = brother;
            }
            else
            {
                ft->rbrother = NULL;
            }
            ft = ft->rbrother;
        }
    }
    return ftRoot;
}

/***
 * 前序访问树节点
 */
void VisitForestHead(ForestHead tr)
{
    if (tr)
    {
        std::cout << tr->data << " ";
        VisitForestHead(tr->lchild);
        VisitForestHead(tr->rbrother);
    }
}

调用函数：

Tree_use.cpp

#include"Trees.h"

int main()
{
    ForestHead tr = NULL;
    tr = CreateForestHead(tr, true); // 根据左孩子，右节点的规则创建树；
    ForestArray *farray = (ForestArray *)malloc(sizeof(ForestArray));
    GetParentArrayTreeList(tr, farray,10);//转化上面的树为 孩子双亲表示法
    ChildTree *rt= TransChildBrother2ChildTree(tr); //孩子兄弟节点转为孩子链表表示法
    VisitByChildTree(rt,10); //访问孩子表示法的节点，打印
    ForestHead tr2 = TransParent2ChildBrother(farray,10); //双亲表示法转换为孩子兄弟表示法
    std::cout<<"按照前序遍历序列访问树节点:"<<std::endl;
    VisitForestHead(tr2);//按照前序遍历序列访问树节点
}

输入参数的例子：

例子1：

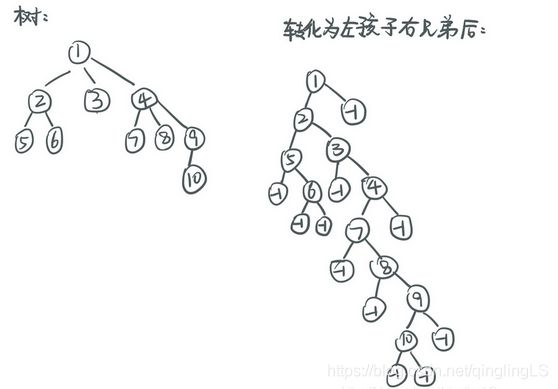
树的形状如下：
按照左孩子右兄弟的二叉树方式输入：
（注意，树的前序遍历=左孩子右兄弟方式存储的二叉树的中序遍历）
也就是：左边的树的前序遍历序列 :1 2 5 6 3 4 7 8 9 10
右边的二叉树的中序遍历序列：1 2 5 6 3 4 7 8 9 10 两个序列是一样的

1
2
5
-1
6
-1
-1
3
-1
4
7
-1
8
-1
9
10
-1
-1
-1
-1
-1

例子2：

树的形状如下：

按照左孩子右兄弟的二叉树方式输入：
也就是：左边的树的前序遍历序列 :3 8 1 7 2 4 6 5 10 9
右边的二叉树的中序遍历序列：3 8 1 7 2 4 6 5 10 9 两个序列是一样的

3
8
1
-1
7
-1
-1
2
-1
4
6
-1
5
10
-1
-1
9
-1
-1
-1
-1

例子2的输出：
1.双亲表示法:

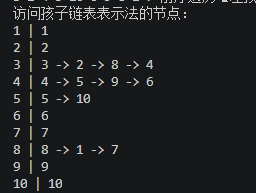
2.孩子链表表示法：
3的孩子节点：8，4，2
4的孩子：6，9，5
8的孩子：1，7
5的孩子：10

3.双亲表示法转换为孩子兄弟表示法：
转换为树之后，利用中序遍历二叉树来检查是否转化正确：

由于转化的过程中，双亲表示法是按照顺序存储了二叉树的值的，所以子节点的顺序发生了变化：
树的结构是下面这样：
孩子的顺序表示被更改了，但是树的关系没有发生变化，
3的孩子节点依然是：8，4，2；4的孩子依然是6，9，5……只是孩子的顺序变化了。

如果是例一的结构，那么孩子的值和顺序不受影响，因为存入数组的顺序是按照data的顺序来存储的。