Rand-RCCA安全接收者匿名

只是学习过程记录供参考,SPHF部分未完
论文：Receiver-anonymity in rerandomizable RCCA-secure cryptosystems resolved(CRYPTO 2021)

SPHF论文参考：
A practical public key cryptosystem provably secure against adaptive chosen ciphertext attack(CRYPTO1998)
Universal hash proofs and a paradigm for adaptive chosen ciphertext secure public-key encryption(EUROCRYPT 2002)

Related Work & Problem：
RCCA：(Crypto2003)Relaxing Chosen-Ciphertext Security
Problem: How to construction an RCCA scheme which is not sd-RCCA?
Rand- RCCA：(Crypto2007)Rerandomizable RCCA encryption
Problem: How to construct Anonymous Rand-RCCA scheme?

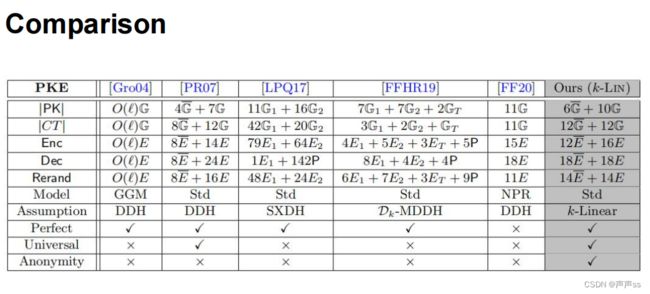
Contribution
• The first receiver-anonymous Rand-RCCA PKE
• Formalize a novel extension of smooth projective hash function with various types of
rerandomizability (Re-SPHF), and redefine the property of smoothness which is crucial
to generally realize Rand-RCCA security with receiver-anonymity

抗选择密文攻击安全，是公钥加密的标准安全性，在这个安全游戏中，敌手在通过与挑战者交互的过程中需要去猜测挑战密文c跟底层明文mb的bit，并且敌手可以去询问解密预言机，这个预言机对任意密文进行解密，如果发现是调整密文会返回abort，所以在这个游戏中，敌手可以根据挑战密文c生成一个新的合法密文，则有能力运用这个解密预言机去赢得游戏。
所以cca安全的加密方案是不允许攻击者对密文本身进行篡改。

但这个安全保证在一些实际的应用场景下会过于强、
考虑一个新的加密方案，他的加密方案是在原有的密文基础上加上一段固定的随机字符串，而在加密的时候是在密文后面的随机字符串先去除，然后使用原来的揭秘方法解密，这样一个新的加密方案显然不满足cca安全，但如果用这个方案进行传输是能够保证安全性的。

所以针对cca安全定义在实际应用场景中过强的问题，03年提出了一个可重放的cca安全，简称RCCA，从这个安全游戏中可以看到，他跟cca最大的区别在于解密预言机的部分
在rcca中解密预言机会对任意的密文进行解密，但是会在发现解密结果等于m0或m1的时候返回replay，也就是说如果敌手直接将挑战密文c询问解密预言机会得到replay，所以如果敌手需要赢得这个game，需要把c篡改成具有不同底层明文的合法密文，才有可能win

Rcca安全的公钥加密方案是不允许攻击者对密文底层的明文进行篡改
Cca是不允许对密文本身进行篡改，即rcca弱化的地方
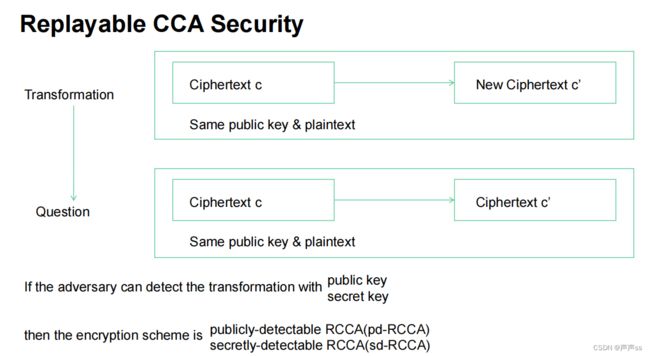在rcca安全的加密方案是可以得到一种变换，就是可以将一个密文变换成一个具有相同公钥，相同底层明文的新的密文。此时有个新的问题，假设给定两个密文c和c’，他们具有相同公钥和底层明文，那么敌手能否这两个密文是否有关联，能否检测出来c’是由c变换过来的。

假如敌手能够凭借pk检测变换的存在，则称这样的rcca加密方案为公开可检测的rcca，简称pdrcca，如果可以凭借sk检测到，则称为秘密可检测rcca，sd-rcca

但当时提出这个概念留下一个公开问题是说是否存在一个rcca方案不属于sd-rcca，就是说即使用sk也无法检测出来，也就是说，变换后的新密文和重新对明文加密得到的新密文是计算性不可区分的
而在这个文章（03）中将拥有这个性质的rcca方案叫做可重随机rcca
所以当时遗留的公开问题就是怎么去构造这种可重随机rcca加密方案，即密文变换后是不可检测的
到了07年提出了可重随机的rcca
密文由四部分组成，跟经典的cramershoup加密方案很相似，由word，message和验证码组成，区别在于c1部分引入了额外的掩码u和z，其中掩码z在加密之前公开选取的，u在加密过程中随机选取，所以后面需要引入c3对u进行额外加密，而引入mask u是为了将c1和c2关联起来，而c2的存在是因为c1引入了mask之后自身是无法进行重随机操作，需要依赖c2，而c2本身能够通过指数计算完成自身rand
后面引入c4辅助c3rerand，使得整个方案实现 不依靠公钥的自身可重随机性

而当rand-rcca应用到隐私保护，比如这个基于混淆网络的秘密通信，图中a1和a2要分别和b1和b2进行通信，但不希望被别人知道通信的对应关系，所以把发送的密文c1和c2发送给混淆服务器，服务器收集到密文会进行统一的重随机操作，再将新的密文分别发给b1和b2，这样其他人就无法将c1和c1*关联起来
所以用rcca实现匿名通信，相比于之前普遍使用cpa具有抗主动攻击性质
但这里还有一个问题，使得他不一定真的能够达到匿名重随机

假如敌手截获到密文c2和c2*，由于这个rerand过程不改变密文底层的公钥信息，所以敌手能够从密文当中收集到底层的公钥信息，那就可以将a2和b2通信者关联起来
这里还需要实现一种匿名性，使得敌手无法根据密文获得pk信息
这也是07年遗留的公开问题

rcca匿名性的定义，在这个game中，挑战者选取两个公钥pk0，pk1发送给敌手，敌手选择一个挑战明文m发送给挑战者，挑战者随机选择一个公钥pkb去对挑战明文m加密，然后将挑战密文c发送给敌手
敌手在交互期间一直可以访问解密预言机，这个跟rcca不一样的是，他在接收到密文之后会同时用sk0和sk1去ci解密，并检查解密结果m0和m1是否有m，如果有则返回replay
所以可以看出，如果敌手能够使用pk对c进行rerand，那么敌手能够利用解密预言机验证猜测结果。
假设挑战者选择b=0，也就是挑战密文的底层公钥是pk0，而正好敌手用pk0对c进行rerand得到新密文，新密文的解密结果是replay，因为可以用sk0正确解密，得到m0=m*如果用错误的pk1得到的密文询问，会得到abort，因为结果的不同敌手就能够猜到pk信息
所以密文是不能允许敌手用pk进行rerand操作的

这也解释了为什么pr方案不满足匿名性，因为他c3和c4部分没有引入mask对rerand进行限制，所以敌手可以用这个漏洞用额外猜测的公钥对后面这两个进行重随机并验证猜测结果。

所以解决思路就是，将前面放在语言和消息部分的mask移到验证码部分，唯一可以自身重随机的方案。并且保留cramer shoup的结构，所以在证明它的安全性和匿名性的时候可以使用平滑投影hash函数去证明

光滑射影哈希函数（SPHF）最初是由Cramer和Shoup 提出的，通常用于构造实用的CCA安全 PKE。
粗略地说，SPHF是一类哈希函数H=（Hsk）sk∈K，由K进行索引，它将非空元素集X映射到哈希值集Π上。每个SPHF都与一个np语言的L⊂X相关联，其中L中的元素在计算上与X \L中的元素难以区分

SPHF的概念可以推广到基于标签的SPHF，其中标签τ也被H（·）、Priv和Pub作为辅助输入。