Pytorch 自定义激活函数前向与反向传播 ReLu系列 含优点与缺点
文章目录
-
- ReLu
-
- 公式
- 求导过程
- 优点:
- 缺点:
- 自定义ReLu
- 与Torch定义的比较
- 可视化
- Leaky ReLu PReLu
-
- 公式
- 求导过程
- 优点:
- 缺点:
- 自定义LeakyReLu
- 与Torch定义的比较
- 可视化
- 自定义PReLu
- ELU
-
- 公式
- 求导过程
- 优点
- 缺点
- 自定义LeakyReLu
- 与Torch定义的比较
- 可视化
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
%matplotlib inline
plt.rcParams['figure.figsize'] = (7, 3.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['axes.unicode_minus'] = False #解决坐标轴负数的铅显示问题
ReLu
线性整流函数 (rectified linear unit)
公式
relu = max ( 0 , x ) = { x , x > 0 0 , x ≤ 0 \text{relu} = \max(0, x) = \begin{cases} x, &x>0 \\ 0, &x\leq 0 \end{cases} relu=max(0,x)={x,0,x>0x≤0
求导过程
f ( x ) 是 连 续 的 f(x)是连续的 f(x)是连续的
f ′ ( x ) = lim h → 0 f ( 0 ) = f ( 0 + h ) − f ( 0 ) h = max ( 0 , h ) − 0 h f'(x)=\lim_{h\to 0}f(0) = \frac{f(0 + h)-f(0)}{h}=\frac{\max(0, h) - 0}{h} f′(x)=limh→0f(0)=hf(0+h)−f(0)=hmax(0,h)−0
lim h → 0 − = 0 h = 0 \lim_{h\to0^-}=\frac{0}{h} = 0 limh→0−=h0=0
lim h → 0 + = h h = 1 \lim_{h\to0^+}=\frac{h}{h} = 1 limh→0+=hh=1
所以 f ′ ( 0 ) f'(0) f′(0)处不可导
所以 f ′ ( x ) = { 1 , x > 0 0 , x < 0 f'(x) = \begin{cases} 1, & x > 0 \\ 0, & x < 0 \end{cases} f′(x)={1,0,x>0x<0
优点:
ReLU激活函数是一个简单的计算,如果输入大于0,直接返回作为输入提供的值;如果输入是0或更小,返回值0。
- 相较于sigmoid函数以及Tanh函数来看,在输入为正时,Relu函数不存在饱和问题,即解决了gradient vanishing问题,使得深层网络可训练
- Relu输出会使一部分神经元为0值,在带来网络稀疏性的同时,也减少了参数之间的关联性,一定程度上缓解了过拟合的问题
- 计算速度非常快
- 收敛速度远快于sigmoid以及Tanh函数
缺点:
- 输出不是zero-centered
- 存在Dead Relu Problem,即某些神经元可能永远不会被激活,进而导致相应参数一直得不到更新,产生该问题主要原因包括参数初始化问题以及学习率设置过大问题
- ReLU不会对数据做幅度压缩,所以数据的幅度会随着模型层数的增加不断扩张,当输入为正值,导数为1,在“链式反应”中,不会出现梯度消失,但梯度下降的强度则完全取决于权值的乘积,如此可能会导致梯度爆炸问题
自定义ReLu
class SelfDefinedRelu(torch.autograd.Function):
@staticmethod
def forward(ctx, inp):
ctx.save_for_backward(inp)
return torch.where(inp < 0., torch.zeros_like(inp), inp)
@staticmethod
def backward(ctx, grad_output):
inp, = ctx.saved_tensors
return grad_output * torch.where(inp < 0., torch.zeros_like(inp),
torch.ones_like(inp))
class Relu(nn.Module):
def __init__(self):
super().__init__()
def forward(self, x):
out = SelfDefinedRelu.apply(x)
return out
与Torch定义的比较
# self defined
torch.manual_seed(0)
relu = Relu() # SelfDefinedRelu
inp = torch.randn(5, requires_grad=True)
out = relu((inp).pow(3))
print(f'Out is\n{out}')
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nFirst call\n{inp.grad}")
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nSecond call\n{inp.grad}")
inp.grad.zero_()
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nCall after zeroing gradients\n{inp.grad}")
Out is
tensor([3.6594, 0.0000, 0.0000, 0.1837, 0.0000],
grad_fn=)
First call
tensor([7.1240, 0.0000, 0.0000, 0.9693, 0.0000])
Second call
tensor([14.2480, 0.0000, 0.0000, 1.9387, 0.0000])
Call after zeroing gradients
tensor([7.1240, 0.0000, 0.0000, 0.9693, 0.0000])
# torch defined
torch.manual_seed(0)
inp = torch.randn(5, requires_grad=True)
out = torch.relu((inp).pow(3))
print(f'Out is\n{out}')
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nFirst call\n{inp.grad}")
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nSecond call\n{inp.grad}")
inp.grad.zero_()
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nCall after zeroing gradients\n{inp.grad}")
Out is
tensor([3.6594, 0.0000, 0.0000, 0.1837, 0.0000], grad_fn=)
First call
tensor([7.1240, 0.0000, 0.0000, 0.9693, 0.0000])
Second call
tensor([14.2480, 0.0000, 0.0000, 1.9387, 0.0000])
Call after zeroing gradients
tensor([7.1240, 0.0000, 0.0000, 0.9693, 0.0000])
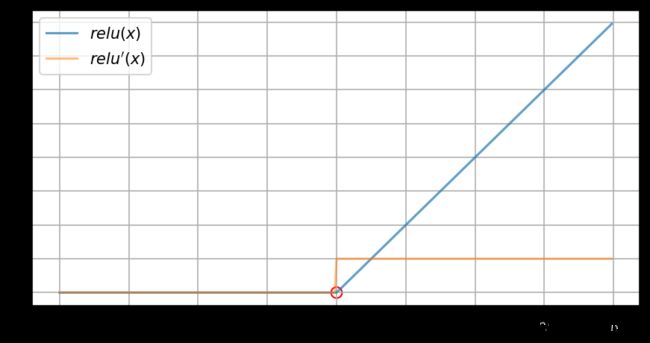
可视化
# visualization
inp = torch.arange(-8, 8, 0.05, requires_grad=True)
out = relu(inp)
out.sum().backward()
inp_grad = inp.grad
plt.plot(inp.detach().numpy(),
out.detach().numpy(),
label=r"$relu(x)$",
alpha=0.7)
plt.plot(inp.detach().numpy(),
inp_grad.numpy(),
label=r"$relu'(x)$",
alpha=0.5)
plt.scatter(0, 0, color='None', marker='o', edgecolors='r', s=50)
plt.grid()
plt.legend()
plt.show()
Leaky ReLu PReLu
公式
leaky_relu = max ( α x , x ) = { x , x ≥ 0 α , x < 0 , α ∈ [ 0 , + ∞ ) \text{leaky\_relu} = \max(\alpha x, x) = \begin{cases} x, & x \ge 0 \\ \alpha, & x < 0 \end{cases} \quad, \alpha \in [0, + \infty) leaky_relu=max(αx,x)={x,α,x≥0x<0,α∈[0,+∞)
while α = 0 , leaky_relu = relu \text{while} \quad \alpha = 0, \text{leaky\_relu} = \text{relu} whileα=0,leaky_relu=relu
求导过程
所以 f ′ ( x ) = { 1 , x ≥ 0 α , x < 0 f'(x) = \begin{cases} 1, & x \ge 0 \\ \alpha, & x < 0 \end{cases} f′(x)={1,α,x≥0x<0
优点:
- 避免梯度消失的问题
- 计算简单
- 针对Relu函数中存在的Dead Relu Problem,Leaky Relu函数在输入为负值时,给予输入值一个很小的斜率,在解决了负输入情况下的0梯度问题的基础上,也很好的缓解了Dead Relu问题
缺点:
- 输出不是zero-centered
- ReLU不会对数据做幅度压缩,所以数据的幅度会随着模型层数的增加不断扩张
- 理论上来说,该函数具有比Relu函数更好的效果,但是大量的实践证明,其效果不稳定,故实际中该函数的应用并不多。
- 由于在不同区间应用的不同的函数所带来的不一致结果,将导致无法为正负输入值提供一致的关系预测。
超参数 α \alpha α 的取值也已经被很多实验研究过,有一种取值方法是对 α \alpha α 随机取值, α \alpha α 的分布满足均值为0,标准差为1的正态分布,该方法叫做随机LeakyReLU(Randomized LeakyReLU)。原论文指出随机LeakyReLU相比LeakyReLU能得更好的结果,且给出了参数 α \alpha α 的经验值1/5.5(好于0.01)。至于为什么随机LeakyReLU能取得更好的结果,解释之一就是随机LeakyReLU小于0部分的随机梯度,为优化方法引入了随机性,这些随机噪声可以帮助参数取值跳出局部最优和鞍点,这部分内容可能需要一整篇文章来阐述。正是由于 α \alpha α 的取值至关重要,人们不满足与随机取样 α \alpha α ,有论文将 α \alpha α 作为了需要学习的参数,该激活函数为 PReLU(Parametrized ReLU)
自定义LeakyReLu
class SelfDefinedLeakyRelu(torch.autograd.Function):
@staticmethod
def forward(ctx, inp, alpha):
ctx.constant = alpha
ctx.save_for_backward(inp)
return torch.where(inp < 0., alpha * inp, inp)
@staticmethod
def backward(ctx, grad_output):
inp, = ctx.saved_tensors
ones_like_inp = torch.ones_like(inp)
return torch.where(inp < 0., ones_like_inp * ctx.constant,
ones_like_inp), None
class LeakyRelu(nn.Module):
def __init__(self, alpha=1):
super().__init__()
self.alpha = alpha
def forward(self, x):
out = SelfDefinedLeakyRelu.apply(x, self.alpha)
return out
与Torch定义的比较
# self defined
torch.manual_seed(0)
alpha = 0.1 # greater so could have bettrer visualization
leaky_relu = LeakyRelu(alpha=alpha) # SelfDefinedLeakyRelu
inp = torch.randn(5, requires_grad=True)
out = leaky_relu((inp).pow(3))
print(f'Out is\n{out}')
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nFirst call\n{inp.grad}")
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nSecond call\n{inp.grad}")
inp.grad.zero_()
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nCall after zeroing gradients\n{inp.grad}")
Out is
tensor([ 3.6594e+00, -2.5264e-03, -1.0343e+00, 1.8367e-01, -1.2756e-01],
grad_fn=)
First call
tensor([7.1240, 0.0258, 1.4241, 0.9693, 0.3529])
Second call
tensor([14.2480, 0.0517, 2.8483, 1.9387, 0.7057])
Call after zeroing gradients
tensor([7.1240, 0.0258, 1.4241, 0.9693, 0.3529])
# torch defined
torch.manual_seed(0)
inp = torch.randn(5, requires_grad=True)
out = F.leaky_relu((inp).pow(3), negative_slope=alpha)
print(f'Out is\n{out}')
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nFirst call\n{inp.grad}")
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nSecond call\n{inp.grad}")
inp.grad.zero_()
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nCall after zeroing gradients\n{inp.grad}")
Out is
tensor([ 3.6594e+00, -2.5264e-03, -1.0343e+00, 1.8367e-01, -1.2756e-01],
grad_fn=)
First call
tensor([7.1240, 0.0258, 1.4241, 0.9693, 0.3529])
Second call
tensor([14.2480, 0.0517, 2.8483, 1.9387, 0.7057])
Call after zeroing gradients
tensor([7.1240, 0.0258, 1.4241, 0.9693, 0.3529])
可视化
# visualization
inp = torch.arange(-8, 8, 0.05, requires_grad=True)
out = leaky_relu(inp)
out.sum().backward()
inp_grad = inp.grad
plt.plot(inp.detach().numpy(),
out.detach().numpy(),
label=r"$leakyrelu(x)$",
alpha=0.7)
plt.plot(inp.detach().numpy(),
inp_grad.numpy(),
label=r"$leakyrelu'(x)$",
alpha=0.5)
plt.scatter(0, 0, color='None', marker='o', edgecolors='r', s=50)
plt.grid()
plt.legend()
plt.show()
自定义PReLu
class SelfDefinedPRelu(torch.autograd.Function):
@staticmethod
def forward(ctx, inp, alpha):
ctx.constant = alpha
ctx.save_for_backward(inp)
return torch.where(inp < 0., alpha * inp, inp)
@staticmethod
def backward(ctx, grad_output):
inp, = ctx.saved_tensors
ones_like_inp = torch.ones_like(inp)
return torch.where(inp < 0., ones_like_inp * ctx.constant,
ones_like_inp), None
class PRelu(nn.Module):
def __init__(self):
super().__init__()
self.alpha = torch.randn(1, dtype=torch.float32, requires_grad=True)
def forward(self, x):
out = SelfDefinedLeakyRelu.apply(x, self.alpha)
return out
ELU
指数线性单元 (Exponential Linear Unit)
公式
elu ( x ) = { x , x ≥ 0 α ( e x − 1 ) , x < 0 \text{elu}(x) = \begin{cases} x, & x \ge 0 \\ \alpha(e^x - 1), & x < 0 \end{cases} elu(x)={x,α(ex−1),x≥0x<0
求导过程
f ′ ( x ) = lim h → 0 f ( 0 ) = f ( 0 + h ) − f ( 0 ) h f'(x)=\lim_{h\to 0}f(0) = \frac{f(0+h)-f(0)}{h} f′(x)=limh→0f(0)=hf(0+h)−f(0)
lim h → 0 − = α ( e h − 1 ) − 0 h = 0 \lim_{h\to0^-}=\frac{\alpha (e^h - 1) - 0}{h} = 0 limh→0−=hα(eh−1)−0=0
lim h → 0 + = h h = 1 \lim_{h\to0^+}=\frac{h}{h} = 1 limh→0+=hh=1
所以 f ′ ( 0 ) f'(0) f′(0)处不可导
所以 f ′ ( x ) = { 1 , x ≥ 0 α e x , x < 0 f'(x) = \begin{cases} 1, & x \ge 0 \\ \alpha e^x, & x < 0 \end{cases} f′(x)={1,αex,x≥0x<0
理想的激活函数应满足两个条件:
- 输出的分布是零均值的,可以加快训练速度。
- 激活函数是单侧饱和的,可以更好的收敛。
LeakyReLU和PReLU满足第1个条件,不满足第2个条件;而ReLU满足第2个条件,不满足第1个条件。两个条件都满足的激活函数为ELU(Exponential Linear Unit)。ELU虽然也不是零均值的,但在以0为中心一个较小的范围内,均值是趋向于0,当然也与 α \alpha α的取值也是相关的。
优点
- ELU具有Relu的大多数优点,不存在Dead Relu问题,输出的均值也接近为0值;
- 该函数通过减少偏置偏移的影响,使正常梯度更接近于单位自然梯度,从而使均值向0加速学习;
- 该函数在负数域存在饱和区域,从而对噪声具有一定的鲁棒性;
缺点
- 计算强度较高,含有幂运算;
- 在实践中同样没有较Relu更突出的效果,故应用不多;
自定义LeakyReLu
class SelfDefinedElu(torch.autograd.Function):
@staticmethod
def forward(ctx, inp, alpha):
ctx.constant = alpha * inp.exp()
ctx.save_for_backward(inp)
return torch.where(inp < 0., ctx.constant - alpha, inp)
@staticmethod
def backward(ctx, grad_output):
inp, = ctx.saved_tensors
ones_like_inp = torch.ones_like(inp)
return torch.where(inp < 0., ones_like_inp * ctx.constant,
ones_like_inp), None
class Elu(nn.Module):
def __init__(self, alpha=1):
super().__init__()
self.alpha = alpha
def forward(self, x):
out = SelfDefinedElu.apply(x, self.alpha)
return out
与Torch定义的比较
# self defined
torch.manual_seed(0)
alpha = 0.5 # greater so could have bettrer visualization
elu = Elu(alpha=alpha) # SelfDefinedLeakyRelu
inp = torch.randn(5, requires_grad=True)
out = elu((inp + 1).pow(3))
print(f'Out is\n{out}')
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nFirst call\n{inp.grad}")
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nSecond call\n{inp.grad}")
inp.grad.zero_()
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nCall after zeroing gradients\n{inp.grad}")
Out is
tensor([ 1.6406e+01, 3.5275e-01, -4.0281e-01, 3.8583e+00, -3.0184e-04],
grad_fn=)
First call
tensor([1.9370e+01, 1.4977e+00, 4.0513e-01, 7.3799e+00, 1.0710e-02])
Second call
tensor([3.8740e+01, 2.9955e+00, 8.1027e-01, 1.4760e+01, 2.1419e-02])
Call after zeroing gradients
tensor([1.9370e+01, 1.4977e+00, 4.0513e-01, 7.3799e+00, 1.0710e-02])
# torch defined
torch.manual_seed(0)
inp = torch.randn(5, requires_grad=True)
out = F.elu((inp + 1).pow(3), alpha=alpha)
print(f'Out is\n{out}')
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nFirst call\n{inp.grad}")
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nSecond call\n{inp.grad}")
inp.grad.zero_()
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nCall after zeroing gradients\n{inp.grad}")
Out is
tensor([ 1.6406e+01, 3.5275e-01, -4.0281e-01, 3.8583e+00, -3.0184e-04],
grad_fn=)
First call
tensor([1.9370e+01, 1.4977e+00, 4.0513e-01, 7.3799e+00, 1.0710e-02])
Second call
tensor([3.8740e+01, 2.9955e+00, 8.1027e-01, 1.4760e+01, 2.1419e-02])
Call after zeroing gradients
tensor([1.9370e+01, 1.4977e+00, 4.0513e-01, 7.3799e+00, 1.0710e-02])
可视化
inp = torch.arange(-1, 1, 0.05, requires_grad=True)
out = F.elu(inp, alpha=1.2)
# out = F.relu(inp)
out.mean(), out.std()
(tensor(0.0074, grad_fn=),
tensor(0.5384, grad_fn=))
inp = torch.arange(-1, 1, 0.05, requires_grad=True)
# out = F.elu(inp, alpha=1)
out = F.relu(inp)
out.mean(), out.std()
(tensor(0.2375, grad_fn=),
tensor(0.3170, grad_fn=))
# visualization
inp = torch.arange(-8, 8, 0.05, requires_grad=True)
out = elu(inp)
out.sum().backward()
inp_grad = inp.grad
plt.plot(inp.detach().numpy(),
out.detach().numpy(),
label=r"$elu(x)$",
alpha=0.7)
plt.plot(inp.detach().numpy(),
inp_grad.numpy(),
label=r"$elu'(x)$",
alpha=0.5)
plt.scatter(0, 0, color='None', marker='o', edgecolors='r', s=50)
plt.grid()
plt.legend()
plt.show()