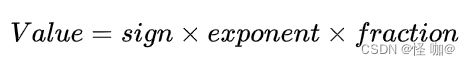BigDecimal使用的时候需要注意什么？

BigDecimal只要涉及到浮点数运算都会用到BigDecimal，并且面试的时候经常会问到，那么BigDecimal使用的时候需要注意什么？

1.为什么不能用浮点数表示金额？

public static void main(String[] args) {
     double a = 7.22 + 7.0;
     double b = 0.09 + 0.01;
     float c = 7.22f + 7.0f;
     System.out.println(a);
     System.out.println(b);
     System.out.println(c);
 }

运行结果：

丢失精度的原因：因为不是所有的小数都能用二进制表示，所以，为了解决这个问题，IEEE 754提出了一种使用近似值表示小数的方式，并且引入了精度的概念。这就是我们所熟知的浮点数。

所以，浮点数只是近似值，并不是精确值，所以不能用来表示金额，否则会有精度丢失。

2.十进制转换二进制

十进制的小数转换为二进制小数，可以采用乘2取整法，主要是利用小数部分乘2，取整数部分，直至小数点后为0。
下面以十进制的0.625为例，将它转化成二进制：

0.2转化二进制：

0.2*2=0.4,整数位为0
0.4*2=0.8,整数位为0
0.8*2=1.6,整数位为1,去掉整数位得0.6
0.6*2=1.2,整数位为1,去掉整数位得0.2
0.2*2=0.4,整数位为0
0.4*2=0.8.整数位为0
就这样推下去！小数*2整,一直下去就行
这个数整不断
0.0011001

十进制数0.2要用二进制数来表示的话，是一个循环小数，无法精确表达。只能根据精度需要，截取小数点后若干位来表示了。因此就会出现丢失精度的问题。

计算机都是以二进制存储，而二进制都是0110，根本没有小数点，我们在电脑计算器当中，十进制转换二进制的时候小数点根本不让你按，为什么呢？因为无限循环小数根本没法使用二进制来精确表示，那遇到浮点数二进制只有0110的计算机是怎么来表示和存储的呢？这就不得不提一下IEEE 754了。

3.科学记数法

提IEEE 754之前我们先来回忆一下科学计数法，科学记数法是一种记数的方法。科学计数法的精妙之处在于，其将"量级"与"数值"两个信息拆分，让使用者对这两个信息更加明确。

数学常识：

• 阶乘是指从1到给定整数n的所有正整数的乘积，用数学符号表示为n!。例如，5!=1×2×3×4×5=120。
• 平方是一种乘方运算，比如，a的平方表示a×a，简写成a²，电脑上可用^代替，例如x^2就是x²的意思。
• 指数是指一个数的幂，或者说是一个数乘自身的次数。在数学中，a的指数记为a ^ n，其中a叫做底数，n叫做指数。例如，2^3=2×2×2=8。
• 如果a ^ x =N（a>0，且a≠1），那么数x叫做以a为底N的对数，${\log }_{a}N$ 读作以a为底N的对数，其中a叫做对数的底数，N叫做真数。一般的计算器当中的log计算就是计算的指数，然后底数默认为10，输入的时候输入的是真数。因此计算这类对数时，直接点击计算机的“log”键，再打上数字就可以算出来指数。

把一个数表示成a与10的n次幂相乘的形式（1≤|a|<10，a不为分数形式，n为整数），这种记数法叫做科学记数法。 例如：19971400000000=1.99714×10^13。计算器或电脑表达10的幂是一般是用E或e，也就是1.99714E13=19971400000000。

用科学记数法表示数时，不改变数的符号，只是改变数的书写形式而已，如：光的速度大约是300,000,000米/秒；这样的数，读、写都很不方便，我们可以免去写这么多重复的0，将其表现为这样的形式：300,000,000=3×10^8， 或者0.00001=1×10^-5，即绝对值小于1的数也可以用科学记数法表示为a乘10 的负n次方的形式。

4.IEEE 754

为了解决部分小数无法使用二进制精确表示的问题,于是就有了IEEE 754规范。IEEE二进制浮点数算术标准（IEEE 754）是20世纪80年代以来最广泛使用的浮点数运算标准，为许多CPU与浮点运算器所采用。

IEEE 754规定了四种表示浮点数值的方式：单精确度（32位）、双精确度（64位）、延伸单精确度（43比特以上，很少使用）与延伸双精确度（79比特以上，通常以80位实现）。其中最常用的就是32位单精度浮点数和64位双精度浮点数。对应的Java当中的float和double。

（1）小数和浮点数的关系：

小数在内存中是以浮点数的形式存储的。浮点数并不是一种数值分类，它和整数、小数、实数等不是一个层面的概念。浮点数是数字（或者说数值）在内存中的一种存储格式，它和定点数是相对的。

Java中使用定点数格式来存储 byte、short、int、long 类型的整数，使用浮点数格式来存储 float、double 类型的小数。整数和小数在内存中的存储格式不一样。

在学习Java语言时，通常认为浮点数和小数是等价的，并没有严格区分它们的概念，这也并没有影响到我们的学习，原因就是浮点数和小数是绑定在一起的，只有小数才使用浮点格式来存储。

其实，整数和小数可以都使用定点格式来存储，也可以都使用浮点格式来存储，但实际情况却是，Java语言使用定点格式存储整数，使用浮点格式存储小数，这是在“数值范围”和“数值精度”两项重要指标之间追求平衡的结果，稍后我会给大家带来深入的剖析。

（2）定点数

所谓定点数，就是指小数点的位置是固定的，不会向前或者向后移动。假设我们用4个字节（32位）来存储无符号的定点数，并且约定，前16位表示整数部分，后16位表示小数部分

如此一来，小数点就永远在第16位之后，整数部分和小数部分一目了然，不管什么时候，整数部分始终占用16位（不足16位前置补0），小数部分也始终占用16位（不足16位后置补0）。

精度： 小数部分的最后一位可能是精确数字，也可能是近似数字（由四舍五入、向零舍入等不同方式得到）；除此以外，剩余的31位都是精确数字。从二进制的角度看，这种定点格式的小数，最多有 32 位有效数字，但是能保证的是 31 位；也就是说，整体的精度为 31~32 位。

（3）为什么要有浮点数？

按照上面提到的16位存储整数，16位存储小数，将内存中的所有位（Bit）都置为 1，值最大为 2^16，换算成十进制为 65 536。很显然精度高，因为所有的位都用来存储有效数字了，缺点是取值范围太小。

太阳质量大约是2000000000000000000000000000000=2×10^30千克（地球的330,000倍），约占太阳系总质量的99.86%。如果使用定点数，这将需要很大的一块内存，大到需要几十个字节。

更加科学的方案是按照 =后面的指数形式（2×10^30）来存储，这样不但节省内存，也非常直观。 这种以指数的形式来存储小数的解决方案就叫做浮点数。浮点数是对定点数的升级和优化，克服了定点数取值范围太小的缺点。

（4）小数以科学计数法表示

IEE754浮点数表示法跟科学计数法表示很像，但又存在一点差距，它属于在2进制的层面来表示。科学计数法是在10进制的层面表示、

将小数转为浮点格式后，小数点为位置发生了浮动，并且 浮动的位数和方向由 E 决定

（5）浮点数的存储

标准的ieee 754格式由三部分组成

• 符号位（Sign Bit）：用于表示数值的正负，0 表示正数，1 表示负数。
• 阶码（Exponent）：用于表示指数部分，通常采用偏移表示法，其中指数值减去一个偏移值来表示实际指数。这允许表示非常大和非常小的数。
• 尾数（Fraction）：用于表示尾数部分，即小数部分。

仍以 19.625 为例，将它转换为科学计数法的浮点数格式：

此时：

• 符号 S 为 0
• 尾数 M 为 1.0011101
• 指数 E 为 4

如你所见，我们需要存储进内存的只有这三项。

Java语言中浮点型分为：

• float：始终占用 4 个字节
• double：始终占用 8 个字节

浮点数的内存分成了三部分，分别用来存储 符号「S」，指数「E」，尾数「M」

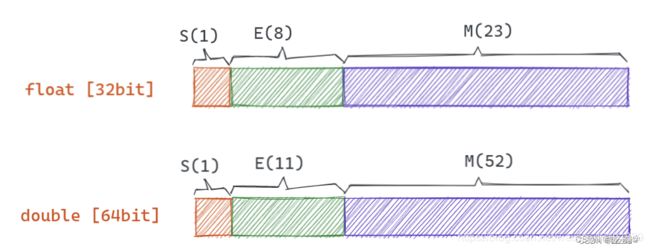
我以网上能找到的ieee 754 float32在线转换器为例，简单易懂。地址：https://www.h-schmidt.net/FloatConverter/IEEE754.html

（6）舍入模式

我们可以尝试着再来一个十进制转二进制无限循环的案例，比如0.2转换二进制0.00110011001100… 会1100的无限循环下去。

• 0.00110011001100 = 1.10011001100*2^-3
• 符号位为0
• 指数为-3，加127为124，二进制为01111100
• 尾数去除整数部分为10011001100110011001100，由于无限循环，所以最后一位直接进1为10011001100110011001101
• 所以0.2在内存中为 0 01111100 10011001100110011001101

浮点数的尾数部分包含的二进制位有限，如果尾数过长，放入内存时必须将多余的位丢掉。

该如何来取这个近似值，IEEE 754 列出了如下四种舍入模式：

（7）总结

• 浮点数通常以二进制科学计数法表示，这意味着它们在表示小数时可能引入舍入误差，从而降低精度。
• 定点数具有较高的精度，可以精确表示小数，因为它们通常以固定小数点位置进行表示。

因此浮点数在精度方面损失不小，但是在取值范围方面增大很多。牺牲精度，换来取值范围，这就是浮点数的整体思想。

IEEE 754 标准其实还规定了浮点数的加减乘除运算，不过本文的重点是讲解浮点数的存储，所以对于浮点数的运算不再展开讨论。

有效数字保留的位数越多说明数值的精确度越高，相对误差较小。

5.在线浮点数转换二进制

在线浮点数转换1：https://www.binaryconvert.com/convert_float.html

在线浮点数转换2：https://www.h-schmidt.net/FloatConverter/IEEE754.html

6.原码、反码、补码

要了解整数是怎么存储的，那就一定要搞清楚原码、反码、补码！

（1）前置概念

计算机底层存储数据时使用的是二进制数字，但是计算机在存储一个数字时并不是直接存储该数字对应的二进制数字，而是存储该数字对应二进制数字的补码。所以接下来我们需要来了解一下原码、反码和补码。

那么再了解原码、反码、补码之前，我们要了解机器数和真值的概念：

1. 机器数：一个数在计算机的存储形式是二进制数，我们称这些二进制数为机器数，机器数是有符号，在计算机中用机器数的最高位存放符号位，0表示正数，1表示负数

2. 真值：因为机器数带有符号位，所以机器数的形式值不等于其真实表示的值（真值），以机器数1000 0001为例，其真正表示的值（首位为符号位）为-1，而形式值（首位就是代表1）为129；因此将带符号的机器数的真正表示的值称为机器数的真值。

（2）原码、反码、补码介绍

一般计算器中十进制转二进制都是返回的补码

（3）数据在计算机中的存储形式

计算机实际只存储补码，所以原码转换为补码的过程，也可以理解为数据存储到计算机内存中的过程：

在原、反、补码中，正数的表示是一模一样的，而负数的表示是不相同的，所以对于负数的补码来说，我们是不能直接用进制转换将其转换为十进制数值的，因为这样是得不到计算机真正存储的十进制数的，所以应该将其转换为原码后，再将转换得到的原码进行进制转换为十进制数（机器数包含符号位）

（4）为何使用原码、反码、补码

我们上面说过，原码、反码、补码的表示对于正数来说都是一样的，而对于负数来说，三种码的表示确是完全不同的，那大家是否会有个疑问：如果原码才是我们人类可以识别并用于直接计算的表示方式，那为什么还会有反码和补码？计算机直接存储原码不就完事了？

在解决这些问题前，我们先来了解计算机的底层概念，我们人脑可以很轻松的知道机器数的第一位是符号位，但对于计算机基础电路设计来说判别第一位是符号位是非常难和复杂的事情，为了让计算机底层设计更加简单，人们开始探索将符号位参与运算，并且采用只保留加法的方法，我们知道减去一个数，等于加上这个数的负数，即：1-1 = 1 + (-1) = 0，这样让计算机运算就更加简单了，并且也让符号位参与到运算中去

总结：减去一个数，等于加上这个数的负数，让符号位参与到加法运算中去

（5）原码、补码、反码演进的过程

提醒：前提是已经完全掌握上面的原码、反码、补码介绍

byte类型的取值范围由其二进制表示决定。在Java中，byte类型的二进制表示是由8个bit组成的。其中，最高位表示符号位，0表示正数，1表示负数。剩下的7个bit用于表示具体的数值。

以有符号的byte类型为例，最小值是-128，其二进制表示为10000000。最大值是127，其二进制表示为01111111。这样，byte类型的取值范围就确定了。

• 127 = 2^7-1
• -128 = -2^7

总结：补码是为了解决正负0的问题，因此就多了一个-128

（6）总结

7.常见面试题

面试题1：为什么浮点类型只有在运算的时候会出现丢失精度的问题，而初始化不会呢？

初始化时通常不会出现精度问题，因为在初始化时可以明确指定初始值，而没有涉及运算。初始化时可以使用特定精度的浮点数值来表示初始值，从而避免舍入误差。

面试题2：float和long哪个存放的数据更大，为什么？

float存放的更大，虽然float占用了4个字节而long占用了8个字节，但是float存储结构不同。他采用了IEEE754的浮点数规范来存储的，也就是把32位分成了两部分，8位存放指数，23位存放尾数。

其中存放指数的8位以无符号形式存储的，因此指数的偏差为其可能值的一半。 对于 float 类型，偏差为 127；对于 double 类型，偏差为 1023。 可以通过将指数值减去偏差值来计算实际指数值。

• 最大正数的符号位 S 肯定是 0，表示正数。
• 指数部分 E 的最大值是全为 1（二进制），即 11111111（二进制），全为1则代表数字255,也就是2的255-127=128次方（127为bias），但是全为1代表特殊值，所以得再减1，就是2的127次方。最小指数位是-126。
• 尾数部分 M 全部为 1，1位隐含位+23位尾数=24位。1.111…111(小数点后23个1) 转换为10进制恰好为1+1/2+1/4+…+(1/2)的23次方=2-(1/2)的23次方=2-2的（-23）次方；
• 最后得出最大值是2 ^ 127×(2-2 ^ -23)≈3.4028235E+38。

long属于采用定点数存储，8个字节也就是64bit，符号位占一位，也就是能存储最大的数大概是2的63次方。

因此单从指数上就已经确定了是float存储的大。

面试题3：什么情况下需要使用BigDecimal？

只要涉及到小数之间运算、小数之间等值判断的一定要用BigDecimal。

面试题4：BigDecimal(double)和BigDecimal(String)有什么区别？

有区别，而且区别很大。因为double是不精确的，所以使用一个不精确的数字来创建BigDeciaml,得到的数字也是不精确的。如0.1这个数字，double只能表示他的近似值。

public static void main(String[] args) {
    BigDecimal doubles = new BigDecimal(0.1);
    BigDecimal String = new BigDecimal("0.1");
    BigDecimal bigDecimal = BigDecimal.valueOf(0.1);
    System.out.println(doubles);
    System.out.println(String);
    System.out.println(bigDecimal);
}

运行结果：

阿里巴巴规范：

BigDecimal.valueOf()是调用Double.toString方法实现的，那么，既然double都是不精确,BigDecimal.valueOf(0.1)怎么保证精确呢？

BigDecimal.valueOf(double) 方法确实是通过将 double 转换为 String 然后再创建 BigDecimal 对象来实现的。这样做是为了避免使用 double 的二进制表示，从而减少精度损失。然而，需要注意的是，由于 double 本身是不精确的浮点数表示，因此在将其转换为 BigDecimal 时，并不能消除 double 的精度问题。

面试题5：BigDecimal原理？

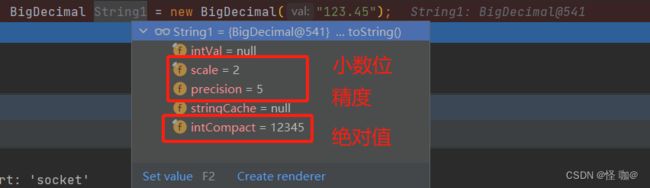
BigDecimal 是 Java 中用于表示精确的十进制数值的类。它可以处理比double和float更大范围的数值，并且可以保证精度不会丢失。它的构造原理主要基于内部的封装了任意精度的整数（unscaled value）和一个标度（scale）的方式来表示十进制数。

我们看一下BigDecimal构造原理：

package java.math;
 
public class BigDecimal {
    //值的绝对long型表示
    private final transient long intCompact;
    //值的小数点后的位数，也称之为标度
    private final int scale;
 
    private final BigInteger intVal;
    //值的有效位数，不包含正负符号，也称之为精度
    private transient int precision;
    private transient String stringCache;
     
    //加、减、乘、除、绝对值
    public BigDecimal add(BigDecimal augend) {}
    public BigDecimal subtract(BigDecimal subtrahend) {}
    public BigDecimal multiply(BigDecimal multiplicand) {}
    public BigDecimal divide(BigDecimal divisor) {}
    public BigDecimal abs() {}
}

以long型的intCompact和scale来存储精确的值。创建BigDecimal对象时，他会优先转换成String类型，比如double转BigDecimal也是先double转成String,再String转成BigDecimal。

在BigDecimal中，每个数值都有一个精度和一个标度。精度是指数值中有效数字的位数，而标度是指小数点后面的位数。例如，对于数值123.45，它的精度是5，标度是2。在进行加、减、乘、除等运算时，BigDecimal会根据数值的精度和标度来进行计算。在计算过程中，它会自动调整数值的精度和标度，以保证计算结果的精度和正确性。

BigDecimal还提供了一些方法来进行数值的格式化和比较。例如，可以使用setScale方法来设置数值的标度，使用compareTo方法来比较两个数值的大小等等。

如果scale为零或正值，则该值表示这个数字小数点右侧的位数。如果scale为负数，则该数字的无标度值需要乘以10的该负数的绝对值的幂。例如，scale为-3，则这个数需要乘1000,即在末尾有3个0。如123.123，那么如果使用BigDecimal表示，那么他的无标度值为123123，他的标度为3。

面试题6：BigDecimal是否可变？

BigDecimal 是不可变的，意味着一旦创建了一个 BigDecimal 对象，它的值不能被更改。并且发生加减乘除操作也都是生成新的对象，这种不可变性有几个重要的原因

• 精确性： BigDecimal 旨在提供精确的十进制数值表示，以避免舍入误差和精度问题。如果 BigDecimal 对象是可变的，那么它的值可能会在不经意间被修改，从而引入精度丢失。不可变性确保了 BigDecimal 对象的值不会被更改，保持了数值的精确性。
• 线程安全：不可变性也使 BigDecimal 对象在多线程环境中更容易管理，因为不需要担心多个线程同时修改对象的值，从而引发竞争条件或并发问题。不可变对象可以在多线程环境中安全地共享，而不需要额外的同步机制。
• 可预测性：不可变性使 BigDecimal 对象的行为更可预测。一旦创建了一个 BigDecimal 对象，它的值在整个程序的生命周期内不会发生变化，这有助于提高代码的可读性和可维护性。
• 安全性：在某些应用中，数值的不可变性也有助于提高安全性。例如，在金融应用程序中，不可变性可以防止恶意修改数值，从而避免潜在的欺诈或数据篡改。

总的来说，BigDecimal 之所以是不可变的，是为了确保精确性、线程安全性、可预测性和安全性。这些特性使其成为处理精确数值的理想选择，特别是在需要高精度的计算和金融领域。

面试题7：BigDecimal的toString()与toPlainString()

BigDecimal 类提供了不同的方法来将 BigDecimal 对象转换为字符串表示。这些方法之间的区别在于它们的输出格式以及如何处理标度（scale）和小数点。

• toPlainString() : 不使用任何指数。
• toString() ：有必要时使用科学计数法。
• toEngineeringString()：有必要时使用工程计数法。 工程记数法是一种工程计算中经常使用的记录数字的方法，与科学技术法类似，但要求10的幂必须是3的倍数

注意：toString()、toEngineeringString()方法在某些时候会使用科学计数法或工程计数法，不是所有情况都会使用科学计数法或工程计数法的

public static void main(String[] args) {
    BigDecimal bg = new BigDecimal("1E11");
    System.out.println(bg.toString()); // 1E+11
    System.out.println(bg.toPlainString()); // 100000000000
    System.out.println(bg.toEngineeringString()); // 100E+9
}

运行结果：

我们看一下源码中toString方法中给的example：

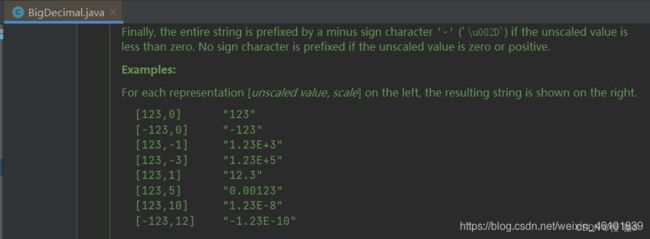
总结了两种toString（）方法会以科学计数方式输出的场景：

• 场景一：scale为负数，一定会转换为科学计数的方式
• 场景二：需要先计算变动指数的值。公式为-scale+(unscaleValue.length-1) ,如果该值小于-6，那么则会使用科学计数的方式输出字符串

场景一测试：

public static void main(String[] args) {
     BigDecimal a = new BigDecimal("2340").setScale(-1);
     System.out.println(a.toString());
     System.out.println(a.toPlainString());
     System.out.println(a.scale());
     System.out.println(a.unscaledValue());
 }

运行结果：

场景二测试：

public static void main(String[] args) {
    //案例一
     BigDecimal b1 = new BigDecimal("0.000000123").setScale(9);
     System.out.println(b1.toString());
     System.out.println(b1.toPlainString());
     System.out.println(b1.scale());
     System.out.println(b1.unscaledValue());
	//输出结果为
     1.23E-7
     0.000000123
     9
     123

	//案例二
     BigDecimal b2 = new BigDecimal("0.000001234").setScale(9);
     System.out.println(b2.toString());
     System.out.println(b2.toPlainString());
     System.out.println(b2.scale());
     System.out.println(b2.unscaledValue());
	//输出结果为
     0.000001234
     0.000001234
     9
     1234

	//案例三
     BigDecimal b3 = new BigDecimal("0.123000000").setScale(9);
     System.out.println(b3.toString());
     System.out.println(b3.toPlainString());
     System.out.println(b3.scale());
     System.out.println(b3.unscaledValue());
	//输出结果为
     0.123000000
     0.123000000
     9
     123000000

	 //案例四
     BigDecimal b4 = new BigDecimal("123000000");
     System.out.println(b4.toString());
     System.out.println(b4.toPlainString());
     System.out.println(b4.scale());
     System.out.println(b4.unscaledValue());
	//输出结果为
     123000000
     123000000
     0
     123000000

	//案例五
	//Double d = 12345678d; Double d = 12345678.0; 效果一样
     Double d = (double) 12345678;
     BigDecimal b5 = BigDecimal.valueOf(d);
     System.out.println(d);
     System.out.println(b5.toString());
     System.out.println(b5.toPlainString());
     System.out.println(b5.scale());
     System.out.println(b5.unscaledValue());
	//输出结果为
     1.2345678E7
     12345678
     12345678
     0
     12345678
 }

如果一个BigDecimal类型的参数toString()是以指数形式返回，那么调用toEngineeringString()则以工程计数法返回，工程计数法返回的10的幂必须是3的倍数

面试题8：为什么不能用BigDecimal的equals方法做等值比较？

因为equals比较的时候会比较标度。new BigDecimal(“0.10000”)和new BigDecimal(“0.1”)这两个数的标度分别是5和1,如果使用BigDecimal的equals方法比较,得到的结果是false。

阿里巴巴规范：

• 等于：new BigDecimal(“123.123”).compareTo(new BigDecimal(“123.123”))==0 —> true
• 小于：new BigDecimal(“123.122”).compareTo(new BigDecimal(“123.123”)) < 0 —> true就证明左边小于右边
• 大于：new BigDecimal(“123.124”).compareTo(new BigDecimal(“123.123”)) > 0 —> true就证明左边大于右边

public static void main(String[] args) {
    BigDecimal bigDecimal = new BigDecimal("0.10000");
    BigDecimal bigDecimal1 = new BigDecimal("0.1");
    System.out.println(bigDecimal1.equals(bigDecimal1));
    System.out.println(bigDecimal.compareTo(bigDecimal1));
}

运行结果：

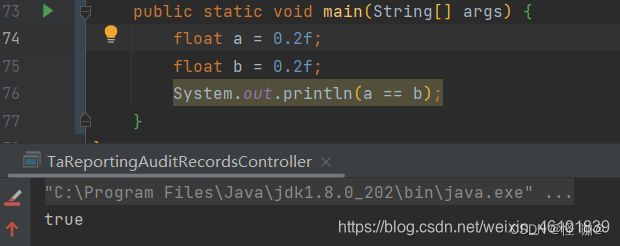
面试题9：浮点数之间不能使用==等值比较？

浮点数一旦发生运算就会丢失精度，正常来说不进行运算，只是简单的比较，==比较没有什么问题。

面试题10：BigDecimal转换String精度丢失问题

在某些情况下，使用 String.format 可能会引入精度丢失问题，特别是当你尝试格式化 BigDecimal 对象时。这是因为 String.format 本质上是基于浮点数格式化的，而浮点数本身存在精度问题。

public static void main(String[] args) {
    BigDecimal price = new BigDecimal("999999.999");

    // 错误示例
    String format = String.format("%.2f", price);
    System.out.println(format);

    // 正确示例（这里就涉及到了小数点的舍去模式，BigDecimal一共提供了8种舍去模式）
    String s = price.setScale(2, RoundingMode.DOWN).toPlainString();
    System.out.println(s);
}

运行结果：

8.总结

1. 不可变性：BigDecimal 是不可变的，一旦创建，它的值不能被更改。因此，在进行任何运算时，需要将结果分配给新的 BigDecimal 对象。
2. 构造方式：在创建 BigDecimal 对象时，最好使用字符串来表示数值，以避免浮点数精度问题。例如，使用 new BigDecimal(“0.1”) 而不是 new BigDecimal(0.1)。
3. 舍入误差：即使使用 BigDecimal，在进行浮点数运算时，仍然可能会引入舍入误差。要注意小数点后的位数，以确保精确性。
4. 使用适当的精度：根据应用程序的需求，选择适当的标度（scale）和精度。如果需要更高的精度，可以增加标度，但要注意性能问题。
5. 精确性和性能权衡：BigDecimal 提供了高精度，但也可能导致性能下降。在某些情况下，你可能需要在精确性和性能之间做权衡，考虑使用其他数据类型或算法来提高性能。
6. 比较和相等性：在比较 BigDecimal 对象时，使用 compareTo 方法来确保精确比较，而不是使用 equals 方法。equals 方法会比较对象引用，而不是值。
7. 避免不必要的运算：在进行 BigDecimal 运算时，避免不必要的运算，以减少计算的复杂性和提高性能。
8. 转换和格式化：在需要将 BigDecimal 转换为其他数据类型或格式化为字符串时，选择适当的方法，如 toPlainString() 或 toEngineeringString()。
9. 错误处理：处理可能的异常，如 ArithmeticException，以应对除以零等异常情况。
10. 协作与库：与其他库和组件一起使用 BigDecimal 时，要了解它们的数值处理方式，以确保一致性和正确性。

总的来说，BigDecimal 是处理高精度数值计算的重要工具，但需要小心处理精度、性能和错误处理等问题，以确保正确性和可靠性。