二叉树的前序遍历、中序遍历、后序遍历(递归+非递归实现)

目录

前序遍历

递归实现

非递归实现

中序遍历 

递归实现

递归实现 

后序遍历

递归实现

非递归实现 

 

---

 

二叉树是一种非常经典的数据结构，它的应用途径十分广泛，但同时它也是一种简单的、易理解的数据结构，解决二叉树问题的核心思想是递归，在初次接触到二叉树这种数据结构时，它的递归方式遍历很容易理解，但当要求以非递归方式来实现遍历时，就显得手足无措了，本篇博客以递归和非递归两种方式实现二叉树的遍历.

前序遍历

前序遍历的顺序为：首先访问根结点，然后遍历左子树，最后遍历右子树(根->左->右).

递归实现

其递归实现十分简单易理解，可以根据其遍历顺序知道，首先访问根结点，然后左子树，最后右子树，只需要了解到其遍历顺序，其余的交给递归去做.

    // 先序遍历
    public void preOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        System.out.print(root.val + " ");
        preOrder(root.left);//遍历左子树
        preOrder(root.right);//遍历右子树
    }

非递归实现

二叉树的非递归遍历主要利用栈来实现，其实现思想与递归实现一致：

1.首先将根结点入栈，并打印根结点；

2.利用栈一直访问根结点的左孩子，直至左孩子为空为止，在访问的过程中，依次打印每个结点并将该结点入栈；

3.之后依次将栈中的存入的结点出栈，对其进行第二步，直至cur == null，且栈为空时，前序遍历结束.

 

    public void preorderTraversal(TreeNode root) {
        Stack stack = new Stack<>();
        TreeNode cur = root;
        while(cur != null || !stack.empty()) {
            while(cur != null) {
                stack.push(cur);
                System.out.print(cur.val + " ");
                cur = cur.left;
            }
            TreeNode top = stack.pop();
            cur = top.right;
        }
    }

中序遍历 

中序遍历的顺序为：首先遍历左子树，然后访问根结点，最后遍历右子树(左->根->右).

递归实现

据其遍历顺序可知，首先遍历访问左子树，然后访问根结点，最后访问右子树，只需要了解到其遍历顺序，其余的交给递归去做.

    // 中序遍历
    public void inOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        inOrder(root.left);
        System.out.print(root.val + " ");
        inOrder(root.right);
    }

递归实现 

其大致思想也是利用栈实现，具体思路如下：

1.若根结点的左孩子不为空，则将根结点入栈，再访问其左孩子，依旧进行这个操作；

2.若根结点的左孩子为空，则输出根结点，然后再判断其右孩子；

3.若不为空，则重复1和2操作，若为空则重复1和2操作

4.若为空，则执行出栈操作，输出栈顶结点，再使当前结点指向top的右孩子，继续进行上述判断，直至cur == null且栈为空时，循环结束，中序遍历完成.

    public List inorderTraversal(TreeNode root) {
        Stack stack = new Stack<>();
        TreeNode cur = root;
        while(cur != null || !stack.empty()) {
            while(cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            TreeNode top = stack.pop();
            System.out.print(top.val + " ");
            cur = top.right;
        }
    }

后序遍历

 后序遍历的顺序为：首先遍历左子树，然后遍历右子树，最后访问根结点(左->右->根).

递归实现

据其遍历顺序可知，首先遍历左子树，然后遍历右子树，最后访问根结点，只需要了解到其遍历顺序，其余的交给递归去做. 

    // 后序遍历
    public void postOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        postOrder(root.left);
        postOrder(root.right);
        System.out.print(root.val + " ");
    }

非递归实现 

二叉树后序遍历非递归实现相较于前序和中序遍历较为麻烦，具体实现思路如下：

1.令cur指向root，若cur不为空，将cur入栈，并将cur置为cur.next，直至cur为空为止；

2.访问栈顶结点，判断其右孩子是否为空或其右孩子等于prev，将结点的值输出，并弹出栈顶元素，此时令top = prev；

3.若不满足2的条件，则cur = cur.next；

4.重复2和3操作，直至cur == null 且栈为空结束循环，后序遍历结束.

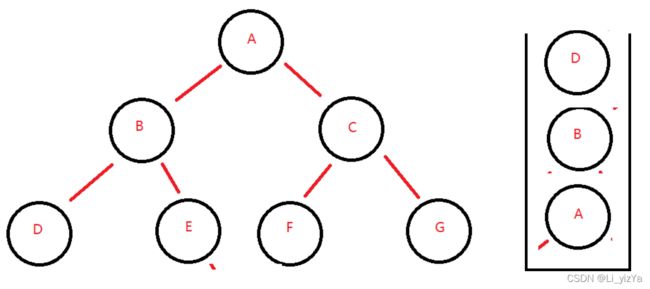
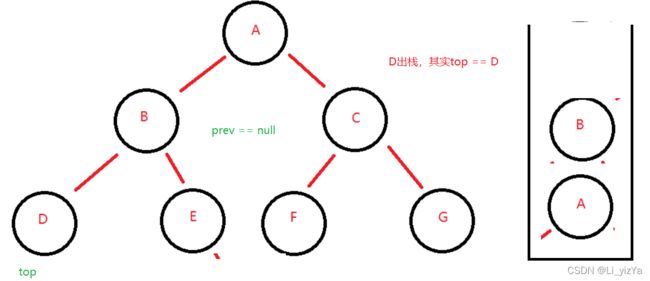
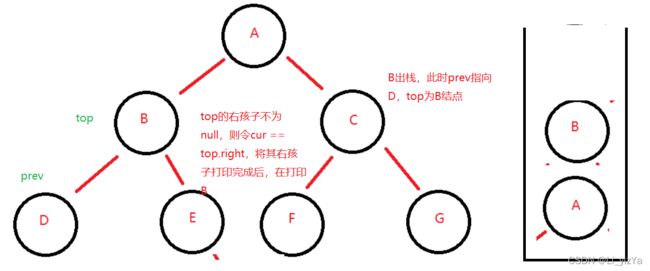
具体过程描述如下图所示，以如下二叉树为例，此时已将所有的左节点入栈：

 

 

上述图片大致描述了二叉树后序遍历的非递归实现方式，具体实现代码：

    public List postorderTraversal(TreeNode root) {
        Stack stack = new Stack<>();
        TreeNode cur = root;
        TreeNode prev = null;
        while (cur != null || !stack.empty()) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            TreeNode top = stack.peek();
            if (top.right == null || top.right == prev) {
                System.out.print(top.val + " ");
                stack.pop();
                prev = top;
            } else {
                cur = top.right;
            }
        }
    }