论文笔记:AAAI 2019 Hypergraph Neural Networks
1. 前言
论文链接:http://gaoyue.org/paper/HGNN.pdf
github:https://github.com/iMoonLab/HGNN
在本文中提出了一个用于数据表示学习的超图神经网络(HGNN)框架,它可以在超图结构中编码高阶数据相关性。面对在实践中学习复杂数据表示的挑战,特别是在处理复杂数据时,超图在数据建模方面更加灵活。该方法设计了超边卷积运算来处理表示学习过程中的数据相关性。通过这种方法,可以有效地利用超边卷积运算来进行传统的超图学习。HGNN能够学习考虑到高阶数据结构的隐含层表示,这是考虑复杂数据相关性的通用框架。我们进行了引文网络分类和视觉对象识别任务的实验,并将HGNN与图卷积网络等传统方法进行了比较。
2. 背景
在现实世界中,复杂的网络关系单纯依靠普通图边的表示有时并不足以很好的阐释,例如在社交网络中推特和微博之间的视觉链接、文字链接、社会性链接。

图1提供了社交媒体数据上的复杂连接示例。
- 一方面,数据相关性可能比两两关系更复杂,难以用普通图结构建模。
- 另一方面,数据表示往往是多模式的,如本例中的视觉连接、文本连接和社会连接。在这种情况下,传统的图结构在表述数据相关性方面存在局限性,这就限制了图卷积神经网络的应用。在这种情况下,进一步研究更好、更通用的数据结构模型来学习表示就显得尤为重要和迫切。
为了解决这一问题,本文提出了一个超图神经网络(HGNN)框架,该框架使用超图结构进行数据建模。与所有边的度都必须为2(一条边仅连接两个节点,因此普通图中边的度为2)的简单图相比,超图可以使用其无限制的度超边编码高阶数据相关性(超越成对连接),如图2所示。在图2中,图是用邻接矩阵表示的,其中每条边仅连接两个顶点。相反,超图可以通过其灵活的超边扩展以实现多模态、异构的数据表示。例如,一个超图可以通过合并邻接矩阵,联合使用多模态数据来生成超图,

因此,hypergraph已经被用于许多计算机视觉任务,如分类和检索任务(Gao et al. 2012)。然而,传统的超图学习方法(Zhou, Huang, and Scholkopf 2007)存在计算复杂度高和存储成本高的问题,限制了超图学习方法的广泛应用。
本文提出的HGNN将复杂数据相关性表述为超图结构,并设计了超边卷积操作,以更好地利用高阶数据相关性进行表示学习。更具体地说,HGNN是一个通用框架,它可以合并多模态数据和复杂的数据相关性。传统的图卷积神经网络可以看作是HGNN的一个特例。为了评估提出的HGNN框架的性能,进行了引文网络分类和视觉对象识别任务的实验。在4个数据集上的实验结果以及与图卷积网络(GCN)等传统方法的比较表明,HGNN具有更好的性能。这些结果表明,本文提出的HGNN方法在学习使用高阶复杂关联表示的数据时更加有效。
本文创新点如下:
- 提出一个超图神经网络框架,即HGNN,用于使用超图结构进行表示学习。HGNN能够通过其超图结构表达复杂的、高阶的数据相关性。并且使用超边卷积操作有效地处理多模态数据/特征。此外,GCN (Kipf和Welling 2017)可以看作是HGNN的一种特殊情况,其简单图中的边可以看作是仅连接两个顶点的2阶超边。
- 该模型在引文网络分类和视觉对象分类任务方面进行了广泛的实验。与最先进的方法的比较证明了所提出的HGNN框架的有效性。实验表明,该方法在处理多模态数据时具有较好的性能。
3. HGNN
3.1 模型框架

从图中大概可以看出来,整个模型的思路是首先将多模态的数据关系作为输入(其中包含训练数据和测试数据),将他们同时考虑进行超边的生成(一种半监督的学习策略,与2017年的经典GCN方法类似,属于一种直推式的学习方法)。将生成的超边组进行超图卷积得到最后的结果,根据下游任务的要求进行输出。
3.2 Hypergraph learning statement
相关超图的定义问题就不再赘述,如果有些概念不清楚可以参考我的前两篇文章
https://blog.csdn.net/qq_44015059/article/details/108871728
https://blog.csdn.net/qq_44015059/article/details/108901941
这里直接给出论文中超图关联矩阵的表达形式

之后考虑下游任务之一的超图节点分类任务(在本文中以引文网络为例),那么这个任务的目标函数可以定义为

其中 Ω ( f ) \Omega(f) Ω(f) 代表超图的规范化处理过程, R e m p ( f ) \mathcal{R}_{emp}(f) Remp(f) 代表监督的损失, f ( ⋅ ) f(\cdot) f(⋅) 代表分类的函数。其中 Ω ( f ) \Omega(f) Ω(f) 被定义为

其中 Δ \Delta Δ 代表一个半正定矩阵,经常被称为超图的拉普拉斯算子。
3.3 Spectral convolution on hypergraph
给出一个超图定义为 G = ( V , E , Δ ) \mathcal{G=(V,E,\Delta)} G=(V,E,Δ) 包含 n n n 个顶点,因为超图的拉普拉斯矩阵 Δ \Delta Δ 是一个 n × n n \times n n×n 的半正定矩阵,因此特征分解后可得 Δ = Φ Λ Φ T \Delta =\Phi \Lambda\Phi^T Δ=ΦΛΦT,由此我们可以得到标准正交特征向量 Φ = d i a g ( ϕ 1 , . . . , ϕ n ) \Phi = diag(\phi_1,...,\phi_n) Φ=diag(ϕ1,...,ϕn) 和 对角矩阵 Λ = d i a g ( λ 1 , . . . , λ n ) \Lambda=diag(\lambda_1,...,\lambda_n) Λ=diag(λ1,...,λn) 包含相应的非负特征值。基于此对于信号 x x x 的傅里叶变换可以定义为 x ^ = Φ T x \hat{x}=\Phi^T x x^=ΦTx。特征向量被视为傅里叶基,特征值被解释为频率。信号 x x x 与滤波器 g g g 的频谱卷积表示为:

其中 ⊙ \odot ⊙ 被定义为哈达姆内积, g ( Λ ) = d i a g ( g ( λ 1 ) , . . . , g ( λ n ) ) g(\Lambda)=diag(g(\lambda_1),...,g(\lambda_n)) g(Λ)=diag(g(λ1),...,g(λn)) 代表傅里叶变换的系数。以此种形式进行运算的算法计算复杂度为 O ( n 2 ) \mathcal{O}(n^2) O(n2)。为了降低算法的时间复杂度,可以利用切比雪夫不等式的一阶近似来拟合卷积核,基于此得到超图的图卷积形式


其中 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1 代表所有结点的参数,为了避免图卷积经常存在的过拟合的问题,论文中将两参数视为单参数的应对这个问题

基于此得到卷积操作的简化形式

其中 ( W + I ) (W+I) (W+I) 可以被认为是超边的权重, W W W 初始化为单位矩阵,这意味着初始条件下每一条超边的权重相等。进而如果存在一个超图信号为 X ∈ R v × C 1 X \in \mathbb{R}^{v \times C_1} X∈Rv×C1,包含 n n n 个节点,特征维度为 C 1 C_1 C1,我们的超边卷积可以定义为

其中 W = d i a g ( w 1 , . . . , w n ) W=diag(w_1,...,w_n) W=diag(w1,...,wn), Θ ∈ R C 1 × C 2 \Theta \in \mathbb{R}^{C_1 \times C_2} Θ∈RC1×C2 是在训练过程中需要学习的参数,核 Θ \Theta Θ 被应用于超图中的所有节点进行特征的提取,在卷积之后可以得到 Y ∈ R n × C 2 Y \in \mathbb{R}^{n \times C_2} Y∈Rn×C2 被用来分类的下游任务
3.4 Hypergraph neural networks analysis
图3展示了HGNN的细节。多模态数据集分为训练数据和测试数据,每个数据包含多个节点特性。然后利用多模态数据集的复杂相关性构造多个超边结构群。之后我们对超边群进行相连操作得到超边的关联矩阵 H H H,将超图的邻域矩阵 H H H 和节点特征输入到HGNN中,得到节点输出标签。如上节所介绍的,我们可以构建超边卷积层 f ( X ; W ; Θ ) f(X;W;Θ) f(X;W;Θ):

其中 X ( l ) ∈ R N × C X^{(l)} \in \mathbb{R}^{N \times C} X(l)∈RN×C 代表超图在第 l l l 层的信号,自然 X ( 0 ) = X X^{(0)}=X X(0)=X 并且 σ \sigma σ 代表非线性激活函数
HGNN模型基于超图上的谱卷积。在这里,进一步研究了HGNN利用数据间高阶相关性的特性。
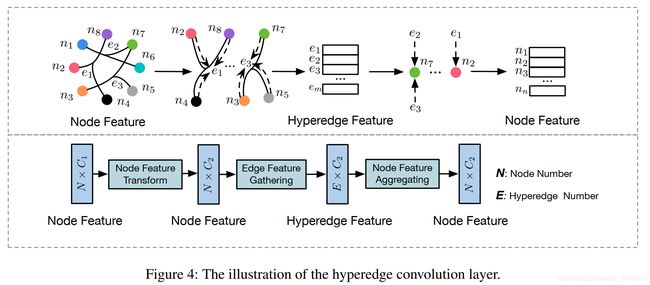
HGNN层可以执行节点-边缘-节点转换,可以使用超图结构更好地细化特性。更具体地说,首先,初始节点功能 X ( 1 ) X^{(1)} X(1) 是由可学习的过滤处理矩阵 Θ ( 1 ) Θ^{(1)} Θ(1) 提取C2-dimensional特性。然后根据超边收集节点特征,形成超边特征 R E × C 2 \mathbb{R}^{E \times C_2} RE×C2,由 H T ∈ R E × N H^T \in \mathbb{R}^{E \times N} HT∈RE×N实现。最后通过矩阵 H H H 的相乘,聚合其相关超边特征得到输出节点特征。表示 D v D_v Dv 和 D e D_e De 在(11)中进行归一化。因此,HGNN层可以通过节点-边缘-节点变换有效地提取超图上的高阶相关性。
3.5 Relations to existing methods
当超边仅连接两个顶点时,将超图简化为一个简单图,且Laplacian ∆ ∆ ∆ 与简单图的Laplacian重合到1 / 2。与已有的图卷积方法相比,HGNN可以自然地建模数据之间的高阶关系,在形成特征提取时有效地利用和编码了这种关系。与传统的超图方法相比,该模型不需要Laplacian ∆ ∆ ∆ 的逆运算,计算效率很高。还需要注意的是,HGNN对多模态特性具有很大的可扩展性,具有超边缘生成的灵活性。
3.6 Implementation
3.6.1 Hypergraph construction
在视觉对象分类任务中, N N N 个视觉对象数据的特征可以表示为 X = [ x 1 , . . . , x n ] T X = [x_1,...,x_n]^T X=[x1,...,xn]T 。我们根据两个特征之间的距离建立超图。具体来说,使用欧几里得距离计算 d ( x i , x j ) d(x_i,x_j) d(xi,xj)。在构造中,每个顶点代表一个可视对象,每个超边由一个顶点与其 K K K 个最近邻连接而成,从而产生 N N N 个超边,连接 K + 1 K + 1 K+1 个顶点。因此,我们得到关联矩阵 H ∈ R N × N H \in \mathbb{R}^{N \times N} H∈RN×N,其中 N × ( K + 1 ) N \times (K + 1) N×(K+1) 项等于1,而其他项等于0。在引文网络分类中,数据以图的结构组织,每个超边都是根据图上的邻接关系将一个顶点与其相邻的顶点连接起来建立的。所以也得到了 N N N 条超边和 H ∈ R N × N H \in \mathbb{R}^{N \times N} H∈RN×N。
3.6.2 Model for node classification
在节点分类问题上,我们构建了如图3所示的HGNN模型。数据集分为训练数据和测试数据。然后构造超图如3.6.1,生成关联矩阵 H H H 和对应的 D e D_e De。我们利用HGNN层强大的能力构建了两层HGNN模型。并利用 s o f t m a x softmax softmax 函数生成预测标签。在训练过程中,训练数据熵损失反向传播更新参数 Θ \Theta Θ,利用测试集标签预测准确率来评估模型性能。当存在多模态信息时,通过构造超边组将其融入其中,然后将各种超边融合在一起,对数据上的复杂关系进行建模。