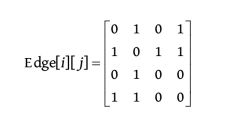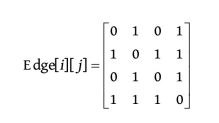算法训练营学习笔记2
树的应用
树
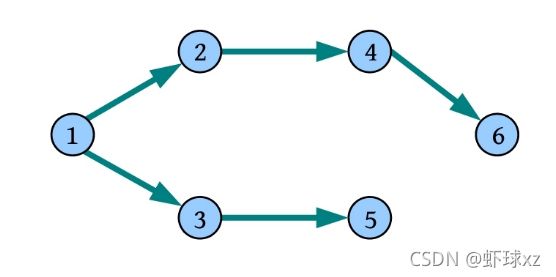
树(Tree)是n (n ≥0)个节点的有限集合,当n =0时,为空树;当n >0时,为非空树。任意一棵非空树,都满足:①有且仅有一个被称为根的节点;②除根节点外的其余节点可分为m (m >0)个互不相交的有限集T 1 , T 2 , …, Tm ,其中每一个集合本身又是一棵树,被称为根的子树(SubTree)
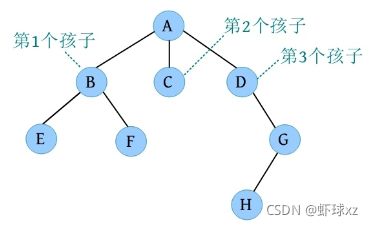
一棵树如下图所示。该树除了树根,还有3棵互不相交的子树:T 1 、T 2 、T 3 。
![]()
该定义是从集合论的角度给出的对树的递归定义,即把树的节点看作一个集合,除了树根,其余节点被分为m 个互不相交的集合,每一个集合又都是一棵树。
树的相关术语较多,在此一一进行介绍。
节点:节点包含数据元素及若干指向子树的分支信息。
节点的度:节点拥有的子树个数。
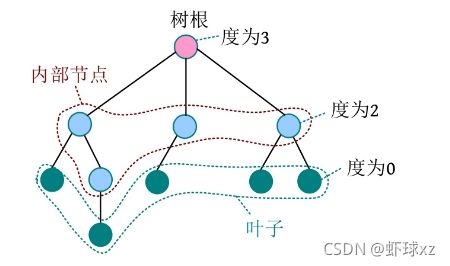
树的度:树中节点的最大度数。
终端节点:度为0的节点,又被称为叶子。
分支节点:度大于0的节点。除了叶子,都是分支节点。
内部节点:除了树根和叶子,都是内部节点。
一棵树如下图所示,该树的度为3,其内部节点和终端节点均用虚线圈起来。
节点的层次:从根到该节点的层数(根节点为第1层)。
树的深度(或高度):所有节点中最大的层数。
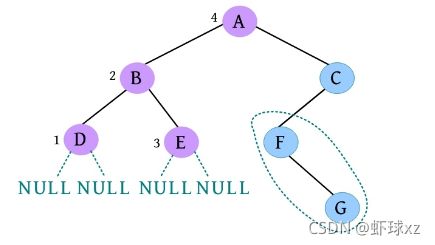
一棵树如下图所示,根为第1层,根的子节点为第2层……该树的最大层次为4,因此树的深度为4。
路径:树中两个节点之间所经过的节点序列。
路径长度:两个节点之间路径上经过的边数。
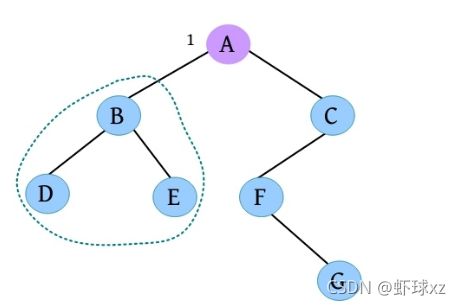
一棵树如下图所示,D到A的路径为D-B-A,D到A的路径长度为2。由于树中没有环,因此树中任意两个节点之间的路径都是唯一的。
如果把树看作一个族谱,就成了一棵家族树,如下图所示
双亲、孩子:节点的子树的根被称为该节点的孩子,反之,该节点为其孩子的双亲
兄弟:双亲相同的节点互称兄弟。
堂兄弟:双亲是兄弟的节点互称堂兄弟。
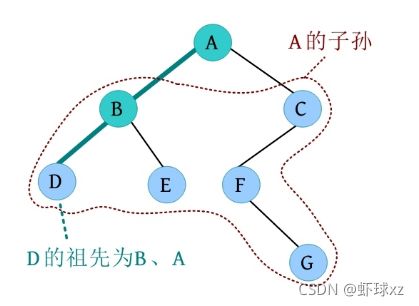
祖先:即从该节点到树根经过的所有节点,被称为该节点的祖先。
子孙:节点的子树中的所有节点都被称为该节点的子孙。
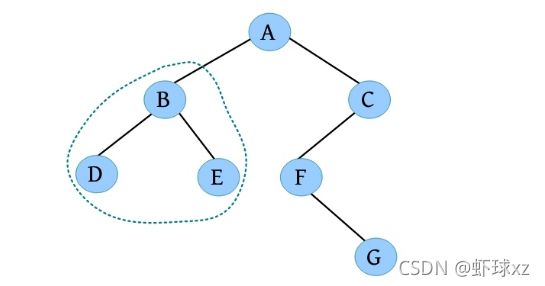
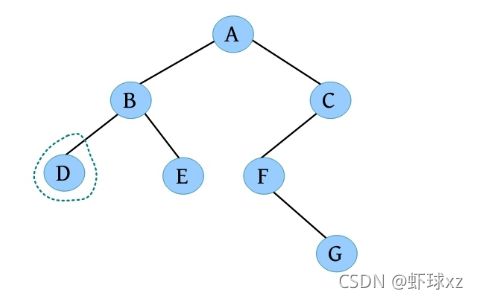
祖先和子孙的关系。如下图所示,D的祖先为B、A,A的子孙为B、C、D、E、F、G。
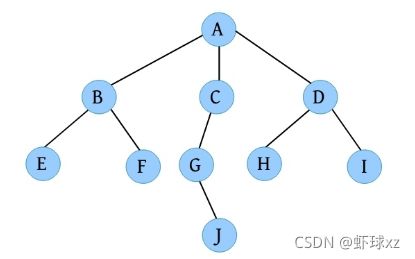
有序树:节点的各子树从左至右有序,不能互换位置,如下图所示。
无序树:节点的各子树可互换位置
森林:由m (m ≥0)棵不相交的树组成的集合。
上图中的树,删除树根A后,余下的3棵子树构成一个森林,如下图所示。
树的存储
树形结构是一对多的关系,除了树根,每个节点都有一个唯一的直接前驱(双亲);除了叶子,每个节点都有一个或多个直接后继(孩子)。那么如何将数据及它们之间的逻辑关系存储起来呢?仍然可以采用顺序存储和链式存储。
- 顺序存储
顺序存储采用一段连续的存储空间,因为树中节点的数据关系是一对多的逻辑关系,所以不仅要存储数据元素,还要存储它们之间的逻辑关系。顺序存储分为双亲表示法、孩子表示法和双亲孩子表示法。
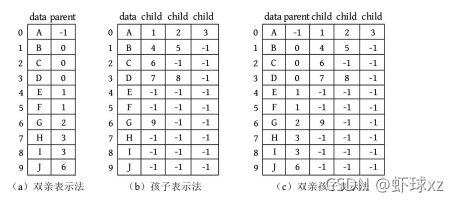
以下图为例,分别讲述三种存储方法。
(1)双亲表示法。除了存储数据元素,还存储其双亲节点的存储位置下标,其中“-1”表示不存在。每个节点都有两个域:数据域data和双亲域parent,如下图(a)所示。树根A没有双亲,双亲被记为-1。B、C、D的双亲为A,而A的存储位置下标为0,因此B、C、D的双亲被记为0。同样,E、F的双亲为B,而B的存储位置下标为1,因此E、F的双亲被记为1。同理,其他节点也这样存储。
(2)孩子表示法。除了存储数据元素,还存储其所有孩子的存储位置下标,如下图(b)所示。A有3个孩子B、C、D,而B、C、D的存储位置下标为1、2、3,因此将1、2、3存入A的孩子域。同样,B有两个孩子E、F,而E、F的存储位置下标为4、5,因此将4、5存入B的孩子域。在本题中,每个节点都被分配了3个孩子域(想一想为什么?),B只有两个孩子,另一个孩子域记为-1,表示不存在。同理,其他节点也这样存储。
(3)双亲孩子表示法。除了存储数据元素,还存储其双亲、所有孩子的存储位置下标,如下图(c)所示。其实就是在孩子表示法的基础上增加了一个双亲域,其他的都和孩子表示法相同,是双亲表示法和孩子表示法的结合体。
三种表示法的优缺点:①双亲表示法只记录了每个节点的双亲,无法直接得到该节点的孩子;②孩子表示法可以得到该节点的孩子,但是由于不知道每个节点到底有多少个孩子,因此只能按照树的度(树中节点的最大度)分配孩子空间,这样做可能会浪费很多空间;③双亲孩子表示法是在孩子表示法的基础上增加了一个双亲域,可以快速得到节点的双亲和孩子,缺点和孩子表示法一样,可能浪费很多空间。
\2. 链式存储
由于树中每个节点的孩子数量无法确定,因此在使用链式存储时,孩子指针域不确定分配多少个合适。如果采用“异构型”数据结构,将每个节点的指针域个数都按照节点的孩子数分配,则数据结构描述困难;如果采用每个节点都分配固定个数的指针域(例如树的度),则浪费很多空间。可以考虑通过两种方法存储:一种采用邻接表的思路,将节点的所有孩子都存储在一个单链表中,称之为孩子链表表示法;另一种采用二叉链表的思路,左指针存储第1个孩子,右指针存储右兄弟,称之为孩子兄弟表示法。
1)孩子链表表示法
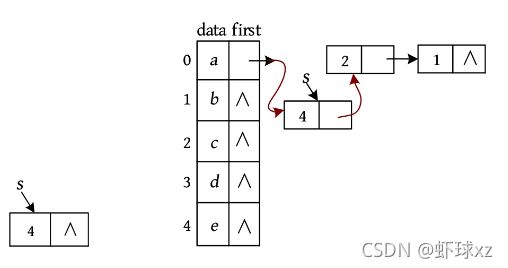
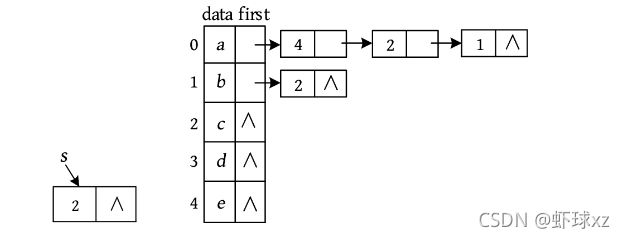
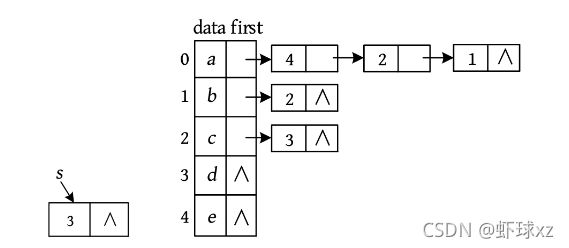
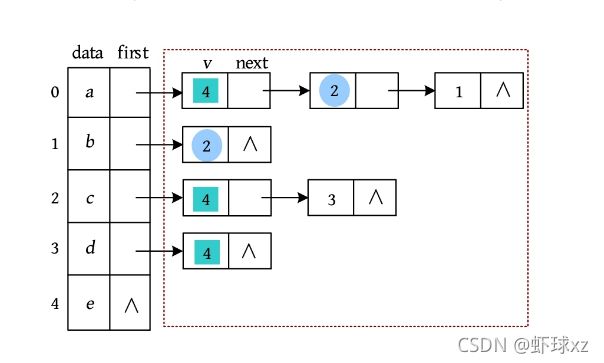
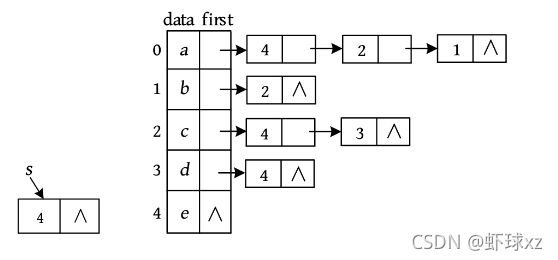
孩子链表表示法类似于邻接表,表头包含数据元素和指向第1个孩子指针,将所有孩子都放入一个单链表中。在表头中,data存储数据元素,first为指向第1个孩子的指针。单链表中的节点记录该节点的下标和下一个节点的地址。上图中的树,其孩子链表表示法如下图所示。
A有3个孩子B、C、D,而B、C、D的存储位置下标为1、2、3,因此将1、2、3放入单链表中,链接在A的first指针域。同样,B有2个孩子E、F,而E、F的存储位置下标为4、5,因此,将4、5放入单链表中,链接在B的first指针域。同理,其他节点也这样存储。
在孩子链表表示法的基础上,如果在表头中再增加一个双亲域parent,则为双亲孩子链表表示法
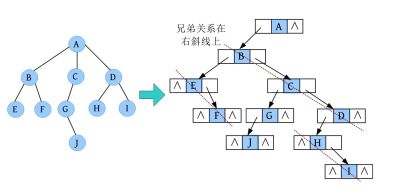
2)孩子兄弟表示法
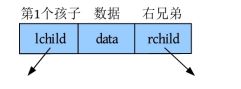
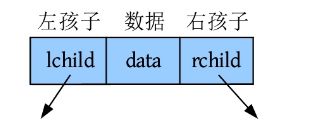
节点除了存储数据元素,还存储两个指针域:lchild和rchild,称之为二叉链表。lchild存储第1个孩子的地址,rchild存储其右兄弟的地址。其节点的数据结构如下图所示。
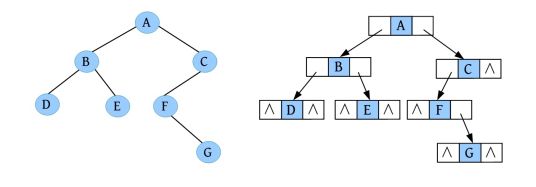
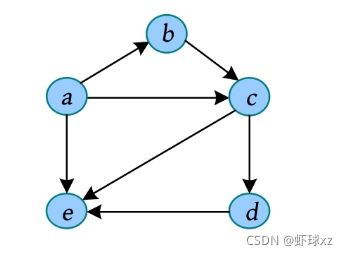
下面左图中的树,其孩子兄弟表示法如下面右图所示。
A有3个孩子B、C、D,其长子(第1个孩子)B作为A的左孩子,B的右指针存储其右兄弟C,C的右指针存储其右兄弟D。
• B有两个孩子E、F,其长子E作为B的左孩子,E的右指针存储其右兄弟F。
• C有1个孩子G,其长子G作为C的左孩子。
• D有两个孩子H、I,其长子H作为D的左孩子,H的右指针存储其右兄弟I。
• G有1个孩子J,其长子J作为G的左孩子。
孩子兄弟表示法的秘籍:将长子当作左孩子,将兄弟关系向右斜。
树、森林与二叉树的转换
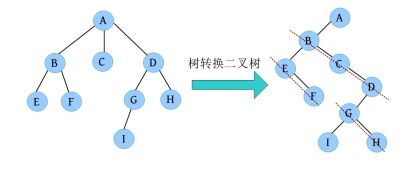
根据树的孩子兄弟表示法,任何一棵树都可以根据秘籍转换为二叉链表存储形式。在二叉链表存储法中,每个节点都有两个指针域,也被称为二叉树表示法。这样,任何树和森林都可以被转换为二叉树,其存储方式就简单多了,这完美解决了树中孩子数量无法确定且难以分配空间的问题。
• A有3个孩子B、C、D,其长子B作为A的左孩子,三兄弟B、C、D在右斜线上。
• B有两个孩子E、F,其长子E作为B的左孩子,两兄弟E、F在右斜线上。
• D有两个孩子G、H,其长子G作为D的左孩子,两兄弟G、H在右斜线上。
• G有1个孩子I,其长子I作为G的左孩子。
那么怎么将二叉树还原为树呢?仍然根据树转换二叉树的秘籍,反操作即可,如下图所示。
B是A的左孩子,说明B是A的长子,B、C、D在右斜线上,说明B、C、D是兄弟,它们的父亲都是A。
• E是B的左孩子,说明E是B的长子,E、F在右斜线上,说明E、F是兄弟,它们的父亲都是B。
• G是D的左孩子,说明G是D的长子,G、H在右斜线上,说明G、H是兄弟,它们的父亲都是D。
• I是G的左孩子,说明I是G的长子。
2)森林和二叉树的转换
森林是由m (m ≥0)棵不相交的树组成的集合。可以把森林中的每棵树的树根都看作兄弟,因此三棵树的树根B、C、D是兄弟,兄弟关系在右斜线上,其他的转换和树转二叉树一样,将长子当作左孩子,将兄弟关系向右斜。 或者把森林中的每一棵树都转换成二叉树,然后把每棵树的根节点都连接在右斜线上即可。
同理,二叉树也可以被还原为森林,如下图所示。B、C、D在右斜线上,说明它们是兄弟,将其断开,那么B和其子孙是第1棵二叉树;C是第2棵二叉树,那么D和其子孙是第3棵二叉树,再按照二叉树还原树的规则,将这3个二叉树分别还原为树即可。
由于在普通的树中,每个节点的子树个数不同,存储和运算都比较困难,因此在实际应用中可以将树或森林转换为二叉树,然后进行存储和运算。二者存在唯一的对应关系,因此不影响其结果。
二叉树
二叉树(Binary Tree)是n (n ≥0)个节点构成的集合,或为空树(n =0),或为非空树。对于非空树T ,要满足:①有且仅有一个被称为根的节点;②除了根节点,其余节点分为两个互不相交的子集T 1 和T 2 ,分别被称为T 的左子树和右子树,且T 1 和T 2 本身都是二叉树。
二叉树是种特殊的树,它最多有两个子树,分别为左子树和右子树,二者是有序的,不可以互换。也就是说,在二叉树中不存在度大于2的节点。
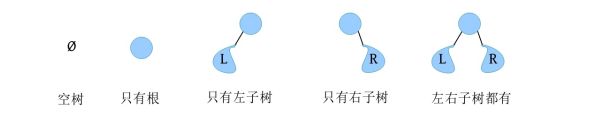
二叉树共有5种形态,如下图所示。
二叉树的结构最简单,规律性最强,因此通常被重点讲解。
二叉树的性质
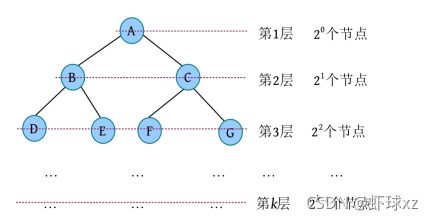
性质1:在二叉树的第 i 层上至多有2 i -1 个节点。
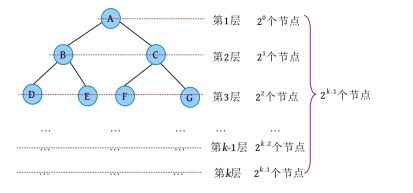
一棵二叉树如下图所示。由于二叉树的每个节点最多有2个孩子,第1层树根为1个节点,第2层最多为2个节点,第3层最多有4个节点,因为上一层的每个节点最多有2个孩子,因此当前层最多是上一层节点数的两倍。
下面使用数学归纳法证明。
• i =1时:只有一个根节点,2 i -1 =20 =1。
• i >1时:假设第i -1层有2 i -2 个节点,而第i 层节点数最多是第i -1层的两倍,即第i 层节点数最多有2×2 i -2 =2 i -1 。
性质2:深度为 k 的二叉树至多有2 k -1个节点。
证明:如果深度为k 的二叉树,每一层都达到最大节点数,如下图所示,则把每一层的节点数加起来就是整棵二叉树的最大节点数。
性质3:对于任何一棵二叉树,若叶子数为 ** n 0 n_0 n0 **,度为2的节点数为 n 2 n_2 n2 ,则 n 0 = n 2 + 1 n_0 =n_2 +1 n0=n2+1。
证明:二叉树中的节点度数不超过2,因此共有3种节点:度为0、度为1、度为2。设二叉树总的节点数为n ,度为0的节点数为n 0,度为1的节点数为n 1 ,度为2的节点数为n 2 ,总节点数等于三种节点数之和,即n =n 0 +n 1 +n 2 。
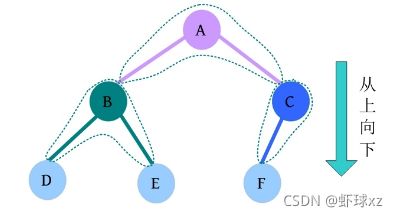
而总节点数又等于分支数b +1,即n =b +1。为什么呢?如下图所示,从下向上看,每一个节点都对应一个分支,只有树根没有对应的分支,因此总的节点数为分支数b +1。
而分支数b 怎么计算呢?从上向下看,如下图所示,每个度为2的节点都产生2个分支,度为1的节点产生1个分支,度为0的节点没有分支,因此分支数b =n 1 +2n 2 ,则n =b +1=n 1 +2n 2 +1。而前面已经得到n =n 0 +n 1 +n 2 ,两式联合得:n 0 =n 2 +1。
有两种比较特殊的二叉树:满二叉树和完全二叉树
满二叉树: 一棵深度为k 且有2 k -1个节点的二叉树。满二叉树的每一层都“充满”了节点,达到最大节点数,如下图所示。
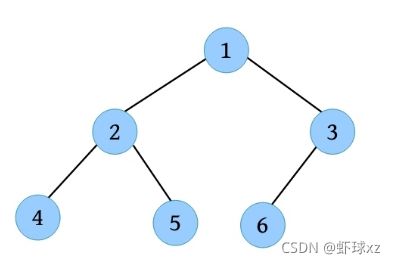
完全二叉树: 除了最后一层,每一层都是满的(达到最大节点数),最后一层节点是从左向右出现的。深度为k 的完全二叉树,当且仅当其每一个节点都与深度为k 的满二叉树中编号为1~n 的节点一一对应。例如,完全二叉树如下图所示,它和上图中的满二叉树编号一一对应。完全二叉树除了最后一层,前面每一层都是满的,最后一层必须从左向右排列。也就是说,如果2没有左孩子,就不可以有右孩子,如果2没有右孩子,则3不可以有左孩子。
性质4:具有n 个节点的完全二叉树的深度必为⌊ l o g 2 n log_2n log2n⌋+1。
证明:假设完全二叉树的深度为k ,那么除了最后一层,前k -1层都是满的,最后一层最少有一个节点,如下图所示。

最后一层最多也可以充满节点,即2 k -1 个节点,如下图所示。
因此,2 k -1 ≤n ≤2 k -1,右边放大后,2 k -1 ≤n <2 k ,同时取对数,k -1≤log2 n <k ,所以k =⌊log2 n ⌋ +1。其中,⌊⌋表示取下限,⌊x ⌋表示小于x 的最大整数,如⌊3.6⌋=3。
例如,一棵完全二叉树有10个节点,那么该完全二叉树的深度为k =⌊log2 10⌋+1=4。
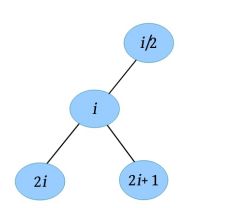
性质5:对于完全二叉树,若从上至下、从左至右编号,则编号为*i* 的节点,其左孩子编号必为2*i* ,其右孩子编号必为2*i* +1;其双亲编号必为*i* /2。
完全二叉树的编号如下图所示。
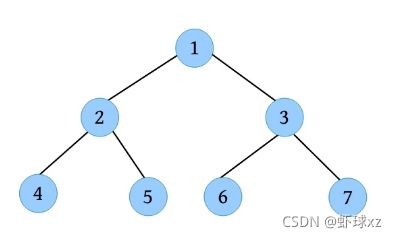
例如,一棵完全二叉树如下图所示。节点2的双亲节点为1,左孩子为4,右孩子为5;节点3的双亲节点为1,左孩子为6,右孩子为7。
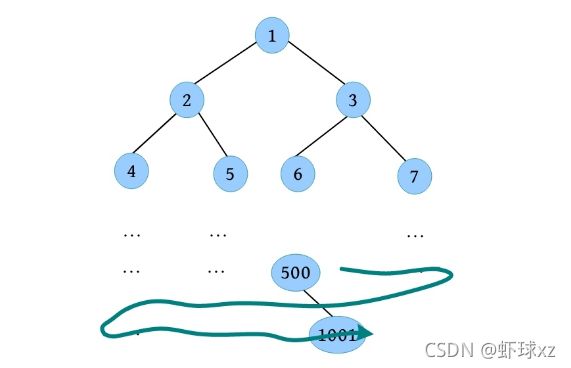
例题1:一棵完全二叉树有1001个节点,其中叶子节点的个数是多少?
首先找到最后一个节点1001的双亲节点,其双亲节点编号为1001/2=500,该节点是最后一个拥有孩子的节点,其后面全是叶子,即1001-500=501个叶子。
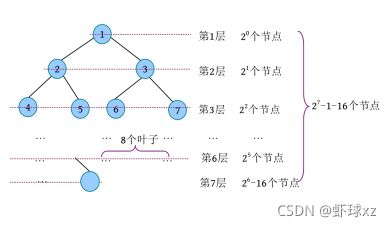
例题2:一棵完全二叉树第6层有8个叶子,则该完全二叉树最少有多少个节点,最多有多少个节点?
完全二叉树的叶子分布在最后一层或倒数第二层。因此该树有可能为6层或7层。
节点最少的情况(6层):8个叶子在最后一层(即第6层),前5层是满的,如下图所示。最少有25 -1+8=39个节点。
节点最多的情况(7层):8个叶子在倒数第2层(即第6层),前6层是满的,第7层最少缺失了8×2个节点,因为第6层的8个叶子如果生成孩子的话,会有16个节点。如下图所示,最多有27 -1-16=111个节点。
二叉树的存储结构
二叉树的存储结构分为两种:顺序存储结构和链式存储结构,下面一一进行讲解。
\1. 顺序存储结构
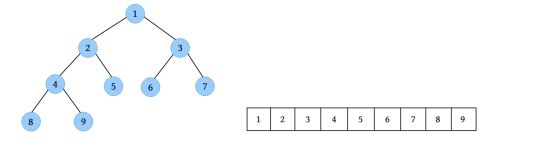
二叉树可以采用顺序存储结构,按完全二叉树的节点层次编号,依次存放二叉树中的数据元素。完全二叉树很适合顺序存储结构,下面左图中的完全二叉树的顺序存储结构如右图所示。
普通二叉树进行顺序存储时需要被补充为完全二叉树,在对应的完全二叉树没有孩子的位置补0,其顺序存储结构如下图所示。
显然,普通二叉树不适合采用顺序存储结构,因为有可能在补充为完全二叉树的过程中,补充了太多的0,而浪费了大量的空间。因此普通二叉树可以使用链式存储结构。
\2. 链式存储结构
二叉树最多有两个“叉”,即最多有两棵子树。
二叉树采用链式存储结构时,每个节点都包含一个数据域,存储节点信息;还包含两个指针域,指向左右两个孩子。这种存储方式被称为二叉链表,结构如下图所示。
二叉链表节点的结构体定义如下图所示。
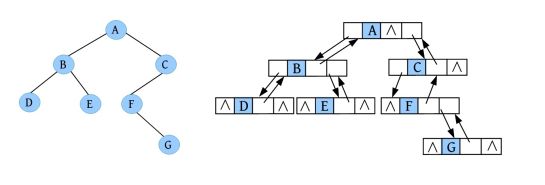
那么下面左图中的二叉树可被存储为二叉链表形式,如下面右图所示。
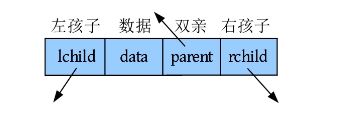
一般情况下,二叉树采用二叉链表存储即可,但是在实际问题中,如果经常需要访问双亲节点,二叉链表存储则必须从根节点出发查找其双亲节点,这样做非常麻烦。例如在上图中,如果想找F的双亲,就必须从根节点A出发,访问C,再访问F,此时才能返回F的双亲为C。为了解决该问题,可以增加一个指向双亲节点的指针域,这样每个节点就包含三个指针域,分别指向两个孩子节点和双亲节点,还包含一个数据域,存储节点信息。这种存储方式被称为三叉链表,结构如下图所示。
三叉链表节点的结构体定义如下图所示。
那么下面左图中的二叉树也可以被存储为三叉链表形式,如下面右图所示
二叉树的创建
如果对二叉树进行操作,必须先创建一棵二叉树。如何创建一棵二叉树呢?从二叉树的定义就可以看出,它是递归定义的(除了根,左、右子树也各是一棵二叉树),因此也可以用递归程序来创建二叉树。
递归创建二叉树有两种方法:询问法和补空法。
\1. 询问法
按照先序遍历的顺序,每次输入节点信息后,都询问是否创建该节点的左子树,如果是,则递归创建其左子树,否则其左子树为空;询问是否创建该节点的右子树,如果是,则递归创建其右子树,否则其右子树为空。
算法步骤:
(1)输入节点信息,创建一个节点T。
(2)询问是否创建T的左子树,如果是,则递归创建其左子树,否则其左子树为NULL。
(3)询问是否创建T的右子树,如果是,则递归创建其右子树,否则其右子树为NULL。
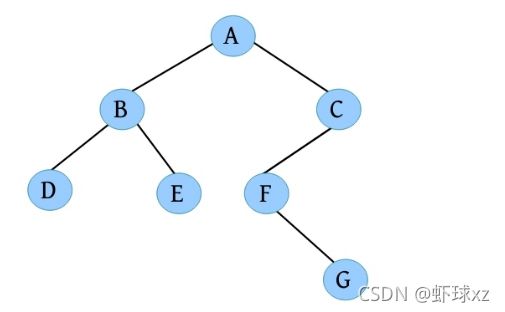
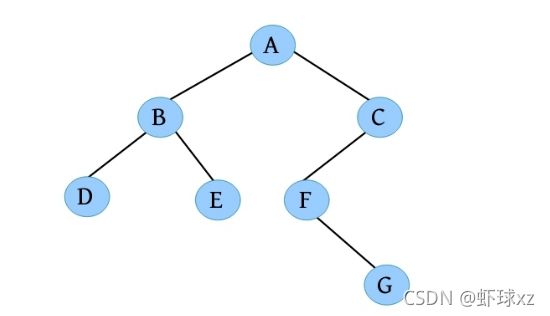
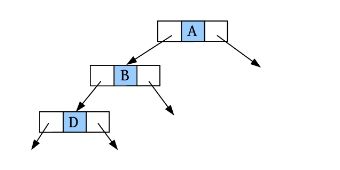
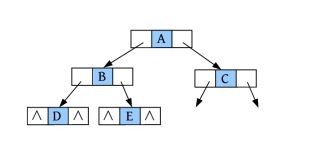
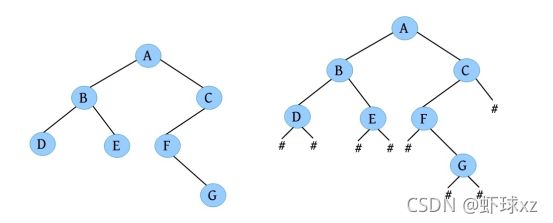
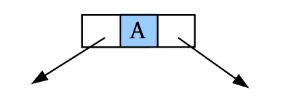
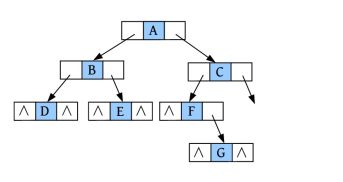
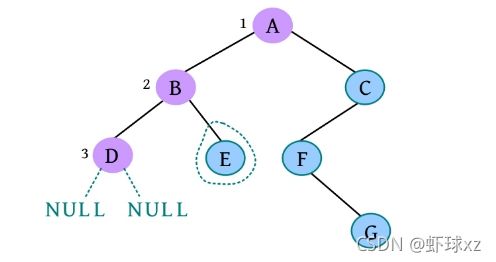
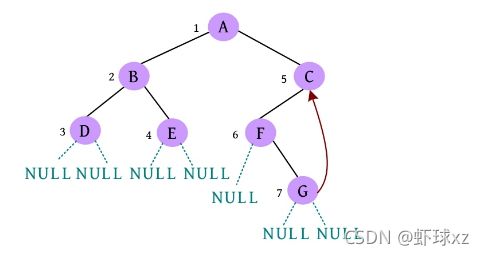
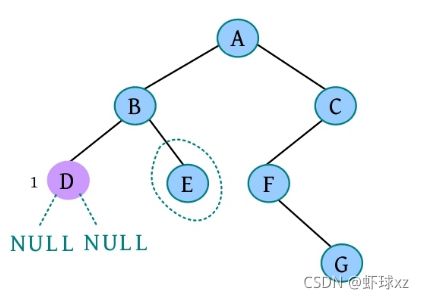
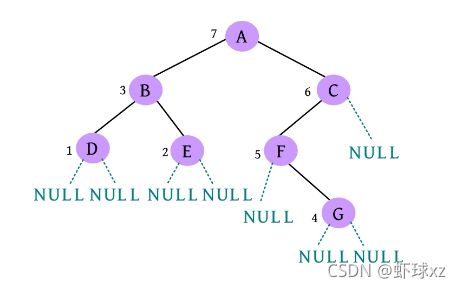
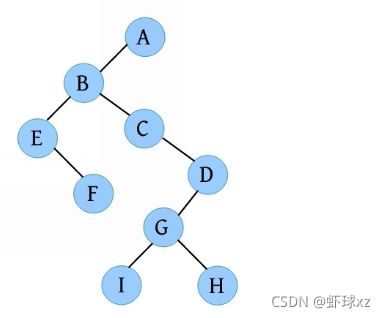
完美图解: 一棵二叉树如下图所示。
该二叉树的创建过程如下。
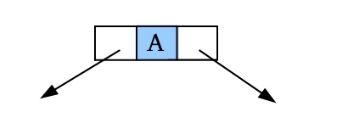
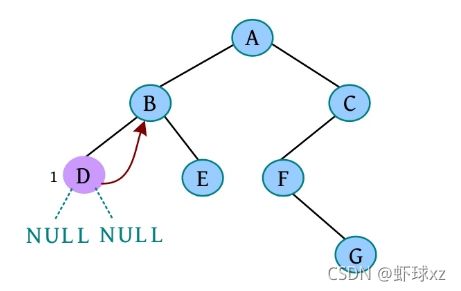
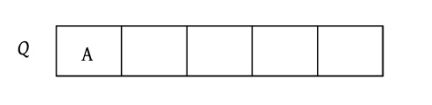
(1)请输入节点信息:A。创建节点A,如下图所示。
(2)是否添加A的左孩子? (Y/N):Y。
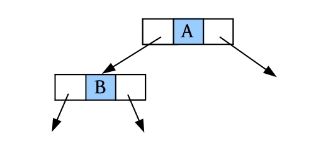
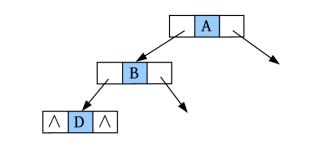
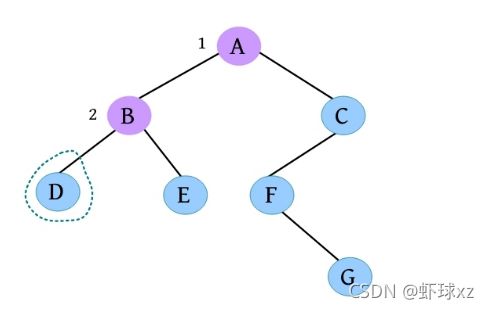
(3)请输入节点信息:B。创建节点B,作为A的左孩子,如下图所示。
(4)是否添加B的左孩子? (Y/N):Y。
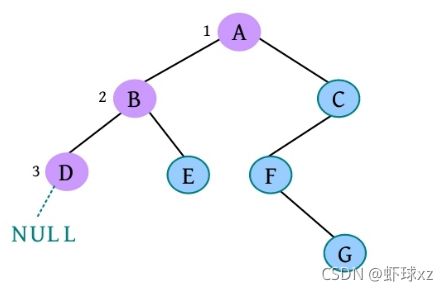
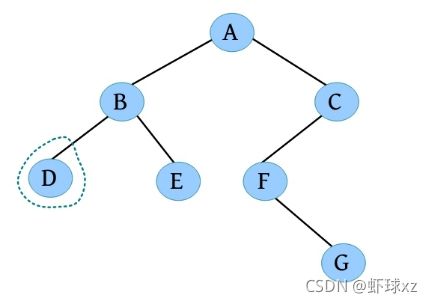
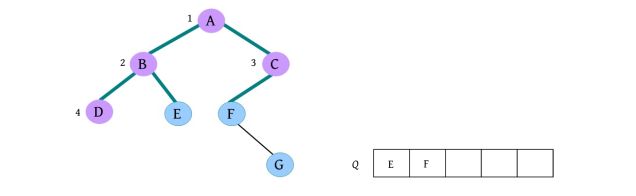
(5)请输入节点信息:D。创建节点D,作为B的左孩子,如下图所示。
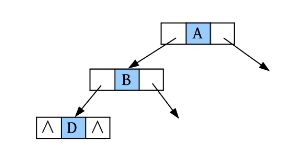
(6)是否添加D的左孩子? (Y/N):N。
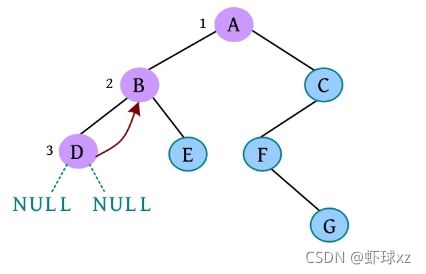
(7)是否添加D的右孩子? (Y/N):N。D左右孩子均为空,如下图所示。
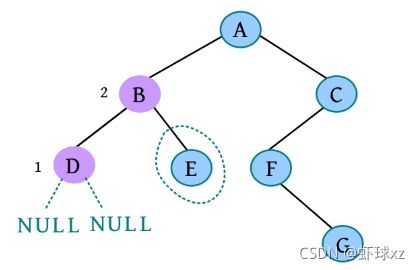
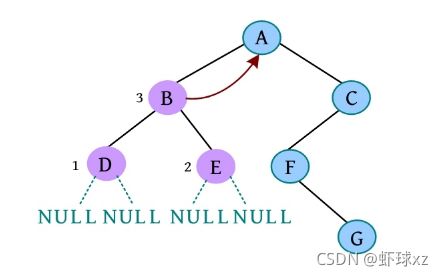
(8)是否添加B的右孩子? (Y/N):Y。
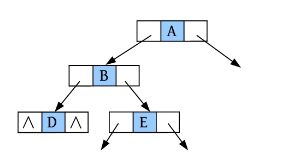
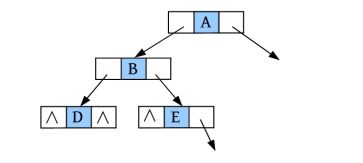
(9)请输入节点信息:E。创建节点E,作为B的右孩子,如下图所示。
(10)是否添加E的左孩子? (Y/N):N。
(11)是否添加E的右孩子? (Y/N):N。E左右孩子均为空,如下图所示。
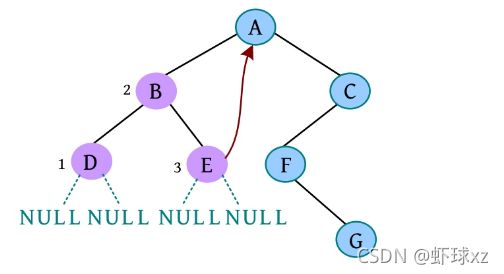
(12)是否添加A的右孩子? (Y/N):Y。
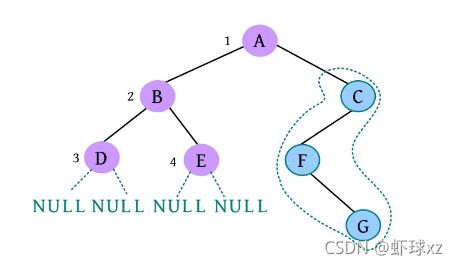
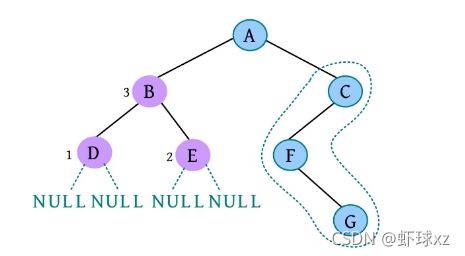
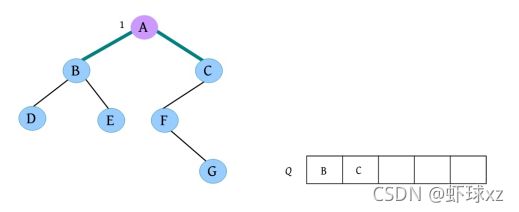
(13)请输入节点信息:C。创建节点C,作为A的右孩子,如下图所示。
(14)是否添加C的左孩子? (Y/N):Y。
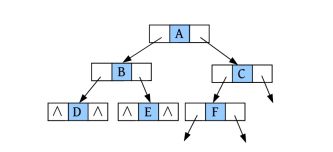
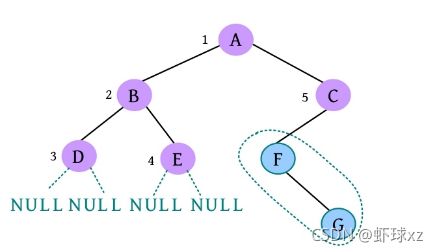
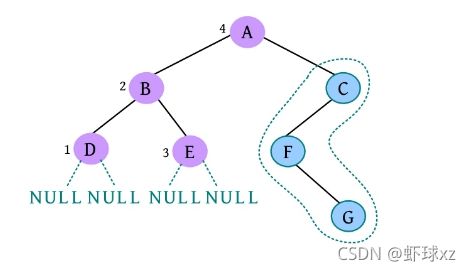
(15)请输入节点信息:F。创建节点F,作为C的左孩子,如下图所示。
![]()
(16)是否添加F的左孩子? (Y/N):N。F的左孩子为空。
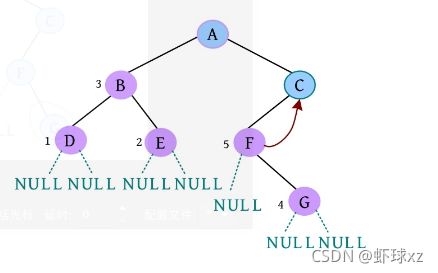
(17)是否添加F的右孩子? (Y/N):Y。
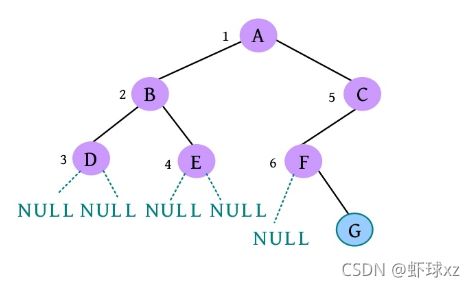
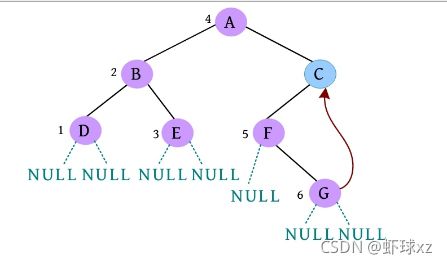
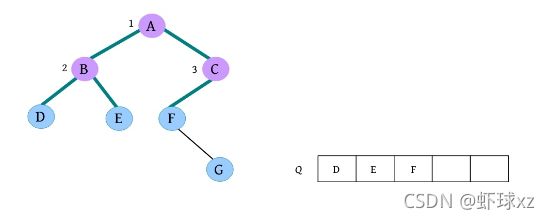
(18)请输入节点信息:G。创建节点G,作为F的右孩子,如下图所示。
(19)是否添加G的左孩子? (Y/N):N。
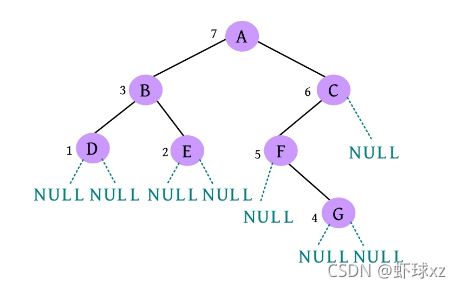
(20)是否添加G的右孩子? (Y/N):N。G左右孩子均为空,如下图所示。
(21)是否添加C的右孩子? (Y/N):N。C右孩子为空,如下图所示。
(22)二叉树创建完毕。
算法代码:
void createtree(Btree &T) //创建二又树函数〈询问法)
{
char check; //判断是否创建左右孩子
T = new Bnode;
cout<<"请输入节点信息:"<<endl;//输入根节点数据
cin>>T->data;
cout<<"是否添加"<<T->data<<"的左孩子? (Y/N)"<<endl;//询问创建了的左子树
cin>>check;
if(check=='Y')
createtree(T->rchild);
else
T->rchild=NULL;
}
\2. 补空法
补空法指如果左子树或右子树为空,则用特殊字符补空,例如“#”。然后按照先序遍历的顺序,得到先序遍历序列,根据该序列递归创建二叉树。
算法步骤:
(1)输入补空后的二叉树先序遍历序列。
(2)如果ch==’#’,则T=NULL;否则创建一个新节点T,令T->data=ch;递归创建T的左子树;递归创建T的右子树。
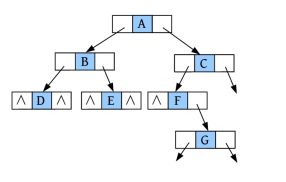
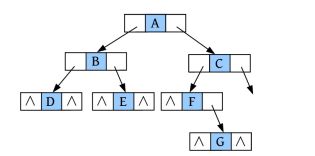
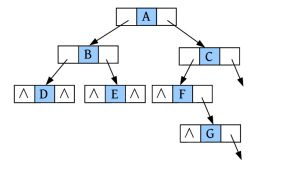
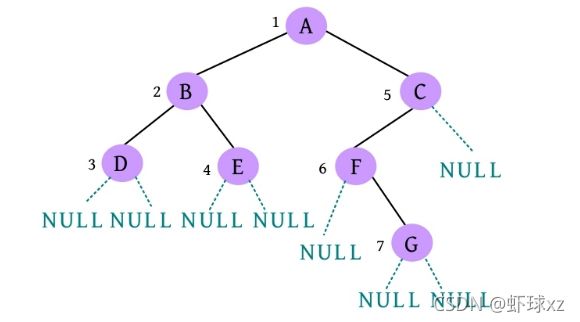
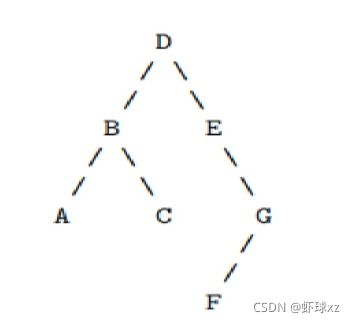
完美图解: 一棵二叉树,将该二叉树补空,在孩子为空时补上特殊符号“#”,如下图所示。
二叉树补空后的先序遍历结果为ABD##E##CF#G###。
该二叉树的创建过程如下。
(1)读取先序序列的第1个字符“A”,创建一个新节点,如下图所示。然后递归创建A的左子树。
(2)读取先序序列的第2个字符“B”,创建一个新节点,作为A的左子树,如下图所示。然后递归创建B的左子树。
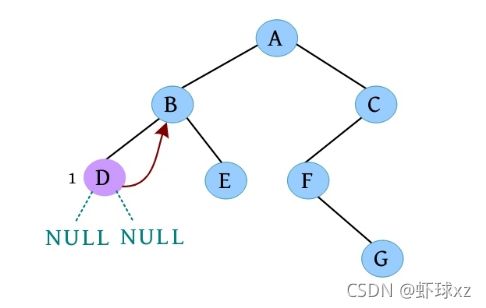
(3)读取先序序列的第3个字符“D”,创建一个新节点,作为B的左子树,如下图所示。然后递归创建D的左子树。
(4)读取先序序列的第4个字符“#”,说明D的左子树为空,如下图所示。然后递归创建D的右子树。
![]()
(5)读取先序序列的第5个字符“#”,说明D的右子树为空,如下图所示。然后递归创建B的右子树。
(6)读取先序序列的第6个字符“E”,创建一个新节点,作为B的右子树,如下图所示。然后递归创建E的左子树。
(7)读取先序序列的第7个字符“#”,说明E的左子树为空,如下图所示。然后递归创建E的右子树。
(8)读取先序序列的第8个字符“#”,说明E的右子树为空,如下图所示。然后递归创建A的右子树。
(9)读取先序序列的第9个字符“C”,创建一个新节点,作为A的右子树,如下图所示。然后递归创建C的左子树。
(10)读取先序序列的第10个字符“F”,创建一个新节点,作为C的左子树,如下图所示。然后递归创建F的左子树。
(11)读取先序序列的第11个字符“#”,说明F的左子树为空,如下图所示。然后递归创建F的右子树。

(12)读取先序序列的第12个字符“G”,创建一个新节点,作为F的右子树,如下图所示。然后递归创建G的左子树。
(13)读取先序序列的第13个字符“#”,说明G的左子树为空,如下图所示。然后递归创建G的右子树。
(14)读取先序序列的第14个字符“#”,说明G的右子树为空,如下图所示。然后递归创建C的右子树。
(15)读取先序序列的第15个字符“#”,说明C的右子树为空,如下图所示。序列读取完毕,二叉树创建成功。
算法代码:
void Createtree(Btree &T)//创建二又树函数〈补空法)
{
char ch;
cin>>ch;//二叉树补空后,按先序遍历序列输入字符
if(ch == '#')
T=NULL;//建空树
else
{
T = new BNode;
T->data=ch;//生成根节点
Createtree(T->lchild);//递归创建左子树
Createtree(T->rchild);//递归创建右子树
}
}
二叉树遍历
二叉树的遍历就是按某条搜索路径访问二叉树中的每个节点一次且仅一次。访问的含义很广,例如输出、查找、插入、删除、修改、运算等,都可以被称为访问。遍历是有顺序的,那么如何进行二叉树的遍历呢?
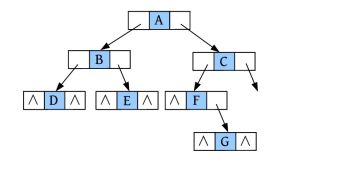
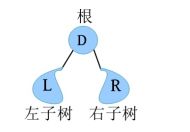
一棵二叉树是由根、左子树、右子树构成的,如下图所示。
那么按照根、左子树、右子树的访问先后顺序不同,可以有6种遍历方案:DLR、LDR、LRD、DRL、RDL、RLD,如果限定先左后右(先左子树后右子树),则只有前3种遍历方案:DLR、LDR、LRD。按照根的访问顺序不同,根在前面的被称为先序遍历(DLR),根在中间的被称为中序遍历(LDR),根在最后的被称为后序遍历(LRD)。
因为树的定义本身就是递归的,因此树和二叉树的基本操作用递归算法很容易实现。下面分别介绍二叉树的3种遍历方法及实现。
先序遍历
先序遍历指先访问根,然后先序遍历左子树,再先序遍历右子树,即DLR。
算法步骤: 如果二叉树为空,则为空操作,否则①访问根节点;②先序遍历左子树;③先序遍历右子树。
先序遍历的秘籍: 访问根,先序遍历左子树,在左子树为空或已遍历时才可以遍历右子树。
完美图解: 一棵二叉树的先序遍历过程如下
(1)访问根节点A,然后先序遍历A的左子树。
(2)访问根节点B,然后先序遍历B的左子树。
(3)访问根节点D,然后先序遍历D的左子树,D的左子树为空,什么也不做,返回。
(4)先序遍历D的右子树,D的右子树为空,什么也不做,返回B。
(5)先序遍历B的右子树。
(6)访问根节点E,先序遍历E的左子树,E的左子树为空,什么也不做,返回。先序遍历E的右子树,E的右子树为空,什么也不做,返回A。
(7)先序遍历A的右子树。
(8)访问根节点C,然后先序遍历C的左子树。
(9)访问根节点F,然后先序遍历F的左子树,F的左子树为空,什么也不做,返回。
(10)先序遍历F的右子树。
(11)访问根节点G,先序遍历G的左子树,G的左子树为空,什么也不做,返回。先序遍历G的右子树,G的右子树为空,什么也不做,返回C。
(12)先序遍历C的右子树,C的右子树为空,什么也不做,遍历结束。
先序遍历序列为ABDECFG。
算法代码:
void preorder(Btree T)
{
if(T)
{
cout<<T->data<<" ";
preorder(T->lchild);
preorder(T->rchild);
}
}
中序遍历
中序遍历指中序遍历左子树,然后访问根,再中序遍历右子树,即LDR。
算法步骤: 如果二叉树为空,则为空操作,否则①中序遍历左子树;②访问根节点;③中序遍历右子树。
中序遍历秘籍: 中序遍历左子树,在左子树为空或已遍历时才可以访问根,中序遍历右子树。
完美图解: 一棵二叉树的中序遍历过程如下。
(1)中序遍历A的左子树,如下图所示。
(2)中序遍历B的左子树,如下图所示。
(3)中序遍历D的左子树,D的左子树为空,则访问D,然后中序遍历D的右子树,D的右子树也为空,则返回B,如下图所示。
(4)访问B,然后中序遍历B的右子树,如下图所示。
(5)中序遍历E的左子树,E的左子树为空,则访问E,然后中序遍历E的右子树,E的右子树也为空,则返回A,如下图所示。
(6)访问A,然后中序遍历A的右子树,如下图所示
(7)中序遍历C的左子树,如下图所示。
(8)中序遍历F的左子树,F的左子树为空,则访问F,然后中序遍历F的右子树。
(9)中序遍历G的左子树,G的左子树为空,则访问G,然后中序遍历G的右子树,G的右子树也为空,则返回C,如下图所示。
(10)访问C,然后中序遍历C的右子树,G的右子树为空,遍历结束,如下图所示。
中序遍历序列为DBEAFGC。
算法代码:
void inorder(Btree T)
{
if(T)
{
inorder(T->lchild);
cout<<T->data<<" ";
inorder(T->rchild);
}
}
后序遍历
后序遍历指后序遍历左子树,后序遍历右子树,然后访问根,即LRD。
算法步骤: 如果二叉树为空,则空操作,否则①后序遍历左子树;②后序遍历右子树;③访问根节点。
后序遍历秘籍: 后序遍历左子树,后序遍历右子树,在左子树、右子树为空或已遍历时才可以访问根。
完美图解: 一棵二叉树的后序遍历过程如下。
(1)后序遍历A的左子树。
(2)后序遍历B的左子树。
(3)后序遍历D的左子树,D的左子树为空,后序遍历D的右子树,D的右子树也为空,则访问D,返回B。
(4)后序遍历B的右子树。
(5)后序遍历E的左子树,E的左子树为空,后序遍历E的右子树,E的右子树也为空,则访问E,此时B的左、右子树都已遍历,访问B,返回A。
(6)后序遍历A的右子树。
(7)后序遍历C的左子树。
(8)后序遍历F的左子树,F的左子树为空,后序遍历F的右子树。
(9)后序遍历G的左子树,G的左子树为空,后序遍历G的右子树,G的右子树也为空,则访问G,此时F的左、右子树都已遍历,访问F,然后返回C。
(10)后序遍历C的右子树,C的右子树为空,此时C的左、右子树都已遍历,访问C,此时A的左、右子树都已遍历,访问A,遍历结束。
后序遍历序列为DEBGFCA。
void posorder(Btree T)
{
if(T)
{
posorder(T->lchild);
posorder(T->rchild);
cout<<T->data<<" ";
}
}
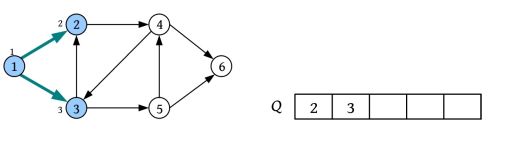
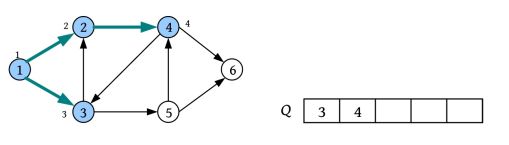
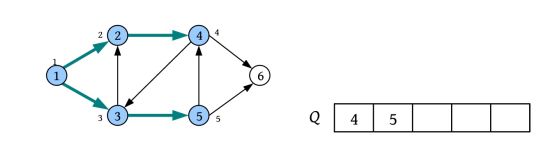
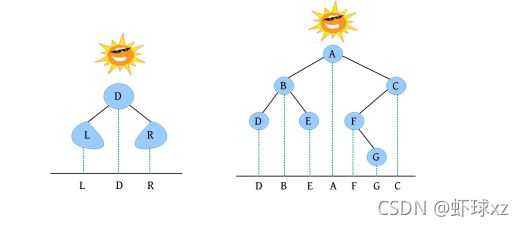
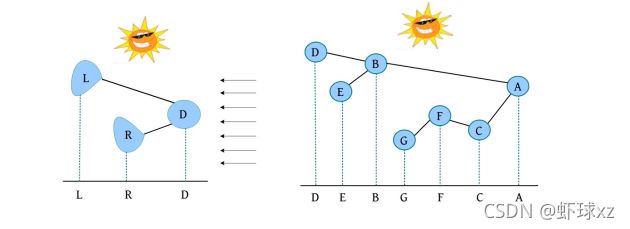
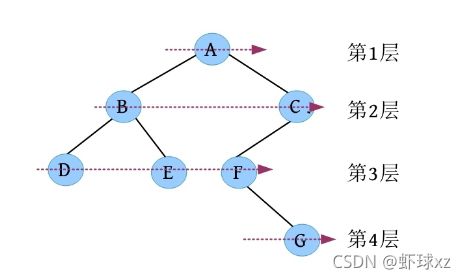
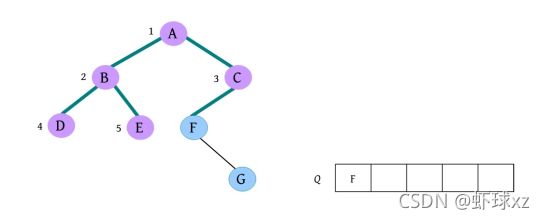
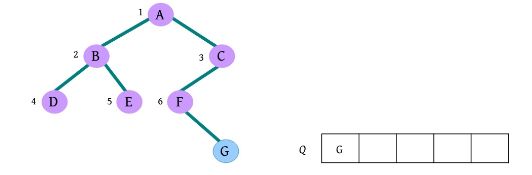
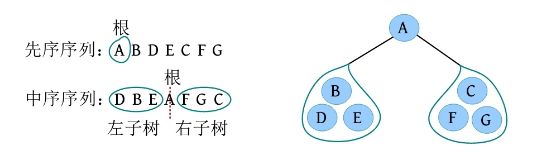
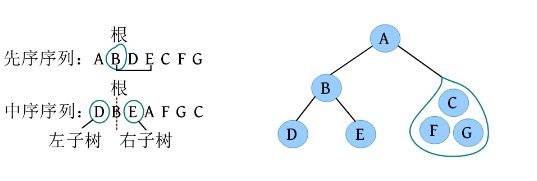
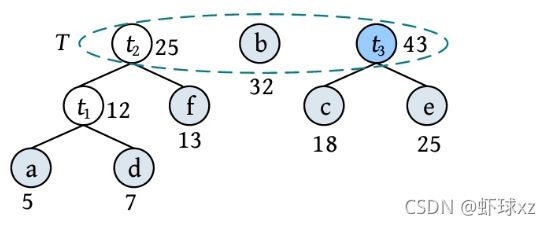
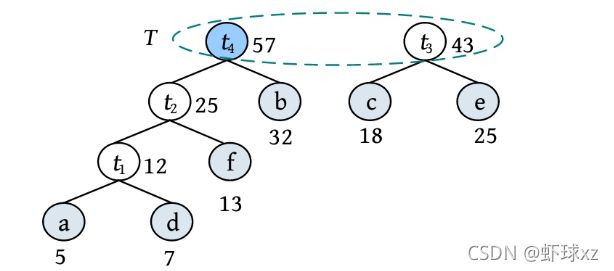
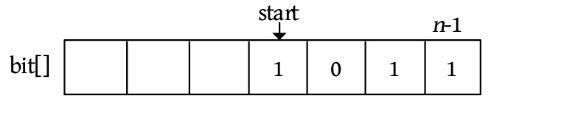
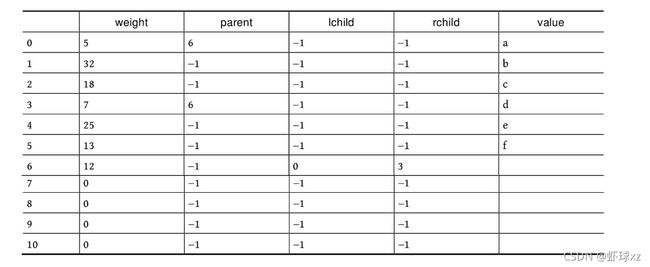
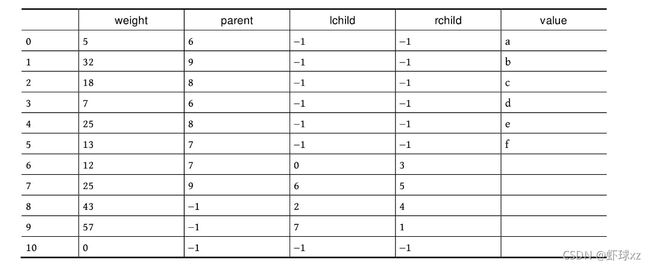
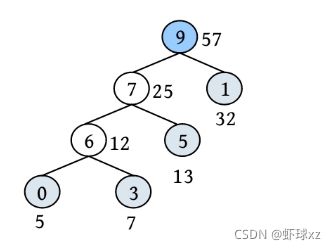
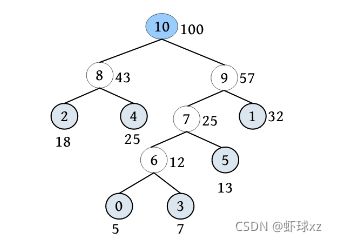
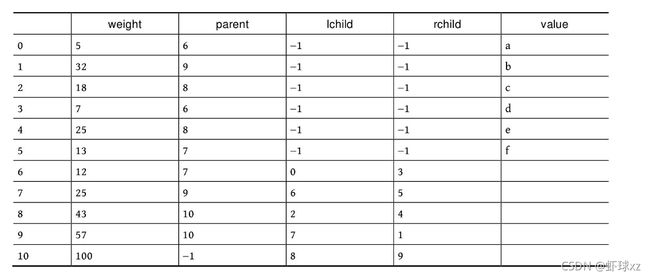
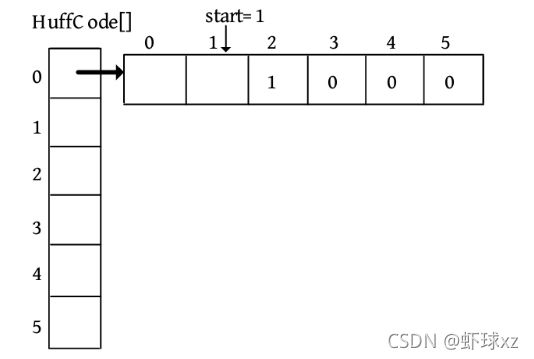
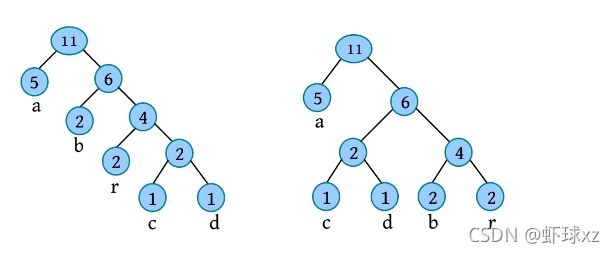
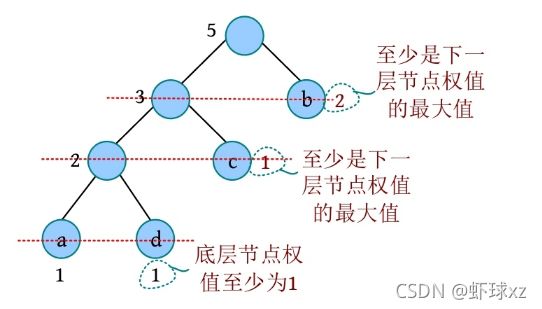
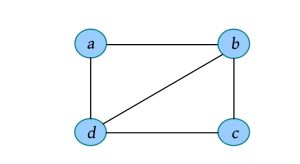
二叉树遍历的代码非常简单明了,“cout 如果不按照程序执行流程,只要求写出二叉树的遍历序列,则还可以使用投影法快速得到遍历序列。 \1. 中序遍历 中序遍历就像在无风的情况下,顺序为左子树、根、右子树,太阳直射,将所有节点都投影到地上。一棵二叉树,其中序序列投影如下图所示。中序遍历序列为DBEAFGC。 \2. 先序遍历 先序遍历就像在左边大风的情况下,将二叉树树枝刮向右方,且顺序为根、左子树、右子树,太阳直射,将所有节点都投影到地上。一棵二叉树,其先序遍历投影序列如下图所示。先序遍历序列为ABDECFG。 \3. 后序遍历 后序遍历就像在右边大风的情况下,将二叉树树枝刮向左方,且顺序为左子树、右子树、根,太阳直射,将所有节点都投影到地上。一棵二叉树,其后序遍历投影序列如下图所示。后序遍历序列为DEBGFCA。 二叉树的遍历一般有先序遍历、中序遍历和后序遍历,除了这三种遍历,还有另一种遍历方式——层次遍历,即按照层次的顺序从左向右进行遍历。 一棵树如下图所示。层次遍历的流程:首先遍历第1层A,然后遍历第2层,从左向右B、C,再遍历第3层,从左向右D、E、F,再遍历第4层G。 层次遍历的秘籍: 首先遍历第1层,然后第2层……同一层按照从左向右的顺序访问,直到最后一层。 程序是怎么实现层次遍历的呢?通过观察可以发现,先被访问的节点,其孩子也先被访问,先来先服务,因此可以用队列实现。 完美图解: 下面以上图的二叉树为例,展示层次遍历的过程。 (1)首先创建一个队列Q ,令树根入队,如下图所示(注意: 实际上是指向树根A的指针入队,为了图解方便,将数据入队)。 (2)队头元素出队,输出A,同时令A的孩子B、C入队(按从左向右的顺序进行,如果是普通树,则包含所有孩子)。二叉树和队列的状态如下图所示。 (3)队头元素出队,输出B,同时令B的孩子D、E入队,如下图所示。 (4)队头元素出队,输出C,同时令C的孩子F入队。二叉树和队列的状态如下图所示。 (5)队头元素出队,输出D,同时令D的孩子入队,D没有孩子,什么也不做。 (6)队头元素出队,输出E,同时令E的孩子入队,E没有孩子,什么也不做。 (7)队头元素出队,输出F,同时令F的孩子G入队。二叉树和队列的状态如下图所示。 (8)队头元素出队,输出G,同时令G的孩子入队,G没有孩子,什么也不做。 (9)队列为空,算法结束。 根据遍历序列可以还原这棵树,包括二叉树还原、树还原和森林还原三种还原方式。 \1. 二叉树还原 由二叉树的先序和中序序列,或者中序和后序序列,可以唯一地还原一棵二叉树。 注意: 由二叉树的先序和后序序列不能唯一地还原一棵二叉树。 算法步骤: (1)先序序列的第1个字符为根; (2)在中序序列中,以根为中心划分左、右子树; (3)还原左、右子树。 完美图解: 已知一棵二叉树的先序序列ABDECFG和中序序列DBEAFGC,还原这棵二叉树。 (1)先序序列的第1个字符A为根,在中序序列中以A为中心划分左、右子树,左子树包含D、B、E三个节点,右子树包含F、G、C三个节点。 (2)左子树DBE,在先序序列中的顺序为BDE,第1个字符B为根,在中序序列中以B为中心划分左、右子树,左、右子树各只有一个节点,直接作为B的左、右孩子。 (3)右子树FGC,在先序序列中的顺序为CFG,第1个字符C为根,在中序序列中以C为中心划分左、右子树,左子树包含F、G节点,右子树为空。 (4)左子树FG,在先序序列中的顺序为FG,第1个字符F为根,在中序序列中以F为中心划分左、右子树,左为空,右子树只有一个节点G,作为F的右孩子即可。 算法代码: 代码解释: 函数有三个参数:pre、mid为指针类型,分别指向先序、中序序列的首地址;len为序列的长度。先序和中序的序列长度一定是相同的。 首先,先序序列的第1个字符pre[0]为根;然后,在中序序列中查找根所在的位置,用index记录查找长度,找到后以根为中心,划分为左、右子树。 左子树:先序序列的首地址为pre+1,中序序列的首地址为mid,长度为index 右子树:先序序列的首地址为pre+index+1,中序序列的首地址为mid+index+1,长度为len-index-1;右子树的长度为总长度减去左子树的长度,再减去根。 确定参数后,再递归求解左、右子树即可。第1次的树根及左、右子树划分如下图所示。 由二叉树的后序序列和中序序列也可以唯一确定一棵二叉树,方法和上面一样,只不过后序序列的最后一个字符为根,然后在中序序列中以根为中心划分左、右子树。 练习: 已知一棵二叉树的后序序列DEBGFCA和中序序列DBEAFGC,还原二叉树。 先序遍历、中序遍历还原二叉树的秘籍:先序找根,中序分左右。 后序遍历、中序遍历还原二叉树的秘籍:后序找根,中序分左右。 \2. 树还原 由于树的先根遍历、后根遍历与其对应二叉树的先序遍历、中序遍历相同,因此可以根据该对应关系,先还原为二叉树,然后把二叉树转换为树。 算法步骤: (1)树的先根遍历、后根遍历与其对应的二叉树的先序遍历、中序遍历相同,因此根据这两个序列,按照先序遍历、中序遍历还原二叉树的方法,还原为二叉树。 (2)将该二叉树转换为树。 已知一棵树的先根遍历序列ABEFCDGIH和后根遍历序列EFBCIGHDA,还原这棵树。 完美图解: (1)树的先根遍历、后根遍历与其对应的二叉树的先序遍历、中序遍历相同,因此其对应二叉树的先序序列ABEFCDGIH和中序遍历序列EFBCIGHDA,按照先序遍历、中序遍历还原二叉树的方法,还原为二叉树,如下图所示。 (2)按二叉树转换树的规则,将该二叉树转换为树,如下图所示。 \3. 森林还原 由于森林的先序遍历、中序遍历与其对应二叉树的先序遍历、中序遍历相同,因此可以根据该对应关系,先将其还原为二叉树,然后将二叉树转换为森林。 已知森林的先序遍历序列ABCDEFGHJI和中序遍历序列BCDAFEJHIG,还原森林。 森林的先序和中序对应二叉树的先序和中序,根据该先序和中序序列先将其还原为二叉树,然后将二叉树转换为森林,如下图所示。 题目描述(P1305) :输入一棵二叉树,输出其先序遍历序列。 输入: 第1行为二叉树的节点数n (1≤n ≤26)。后面的n 行,以每一个字母为节点,后两个字母分别为其左、右孩子。对空节点用*表示。 输出: 输出二叉树的先序遍历序列。 题解: 可用静态存储方式,存储每个节点的左、右孩子,然后按先序遍历顺序输出。 算法代码: 题目描述(UVA536): 小瓦伦丁非常喜欢玩二叉树。她最喜欢的游戏是根据二叉树节点的大写字母随机构造的。 为了记录她的树,她为每棵树都写下两个字符串:一个先序遍历(根、左子树、右子树)和一个中序遍历(左子树、根、右子树)。上图所示的树,先序遍历是DBACEGF,中序遍历是ABCDEFG。她认为这样一对字符串可以提供足够的信息,以便以后重建这棵树。 输入: 输入包含一个或多个测试用例。每个测试用例都包含一行,其中包含两个字符串,表示二叉树的先序遍历和中序遍历。两个字符串都由唯一的大写字母组成。 输出: 对于每个测试用例,都单行输出该二叉树的后序遍历序列(左子树、右子树、根)。 题解: 本题给出二叉树的先序和中序序列,要求输出后序序列。无须构建二叉树,只需在还原二叉树的同时,输出后序序列即可。根据先序序列找根,以中序序列划分左、右子树。 题目描述(UVA548): 确定给定二叉树中的一个叶子节点,使从根到叶子路径上的节点权值之和最小。 输入: 输入包含二叉树的中序遍历和后序遍历。从输入文件中读取两行(直到文件结束)。第1行包含与中序遍历相关联的值序列,第2行包含与后序遍历相关联的值序列。所有值均不同,都大于零且小于10000。假设没有二叉树超过10000个节点或少于1个节点。 输出: 对于每棵二叉树,都输出值最小的路径上叶子节点的值。如果多条路径的值最小,则选择叶子节点值最小的路径。 通常的编码方法有固定长度编码和不等长编码两种。这是一个设计最优编码方案的问题,目的是使总码长度最短。这个问题是利用字符的使用频率来编码,是不等长编码方法,使得经常使用的字符编码较短,不常使用的字符编码较长。如果采用等长的编码方案,假设所有字符的编码都等长,则表示n 个不同的字符需要⌈logn ⌉位。例如3个不同的字符a 、b 、c ,至少需要两位二进制数表示,即a :00、b :01、c :10。如果每个字符的使用频率都相等,则固定长度编码是空间效率最高的方法。 不等长编码方法需要解决两个关键问题:①编码尽可能短,我们可以让使用频率高的字符编码较短,使用频率低的字符编码较长,这种方法可以提高压缩率,节省空间,也能提高运算和通信速度,即频率越高,编码越短;②不能有二义性。 例如:ABCD四个字符如果这样编码: 那么现在有一列数0110,该怎样翻译呢?是翻译为ABBA、ABD、CBA还是CD?这种混乱的译码如果用在军事情报中后果会很严重!那么如何消除二义性呢?解决的办法是:任何一个字符的编码都不能是另一个字符编码的前缀,即前缀码特性。 1952年,数学家D.A.Huffman提出了一种最佳编码方式,被称为哈夫曼(Huffman)编码。哈夫曼编码很好地解决了上述两个关键问题,被广泛地应用于数据压缩,尤其是远距离通信和大容量数据存储。常用的JPEG图片就是采用哈夫曼编码压缩的。 哈夫曼编码的基本思想是以字符的使用频率作为权值构建一棵哈夫曼树,然后利用哈夫曼树对字符进行编码。构造一棵哈夫曼树,是将所要编码的字符作为叶子节点,将该字符在文件中的使用频率作为叶子节点的权值,以自底向上的方式,通过n -1次的“合并”运算后构造出的树。其核心思想是让权值大的叶子离根最近。 哈夫曼算法采取的贪心策略是,每次都从树的集合中取出没有双亲且权值最小的两棵树作为左、右子树,构造一棵新树,新树根节点的权值为其左、右孩子节点权值之和,将新树插入树的集合中。 \1. 算法步骤 (1)确定合适的数据结构。编写程序前需要考虑的情况如下。 在哈夫曼树中,如果没有度为1的节点,则一棵有n 个叶子节点的哈夫曼树共有2n -1个节点(n -1次的“合并”,每次都产生一个新节点)。 构成哈夫曼树后,编码需要从叶子节点出发走一条从叶子到根的路径。译码需要从根出发走一条从根到叶子的路径。那么对于每个节点而言,需要知道每个节点的权值、双亲、左孩子、右孩子和节点的信息。 (2)初始化。构造n 棵节点为n 个字符的单节点树集合T ={t 1 ,t 2 ,t 3 ,…,tn },每棵树只有一个带权的根节点,权值为该字符的使用频率。 (3)如果在T 中只剩下一棵树,则哈夫曼树构造成功,跳到第6步。否则,从集合T 中取出没有双亲且权值最小的两棵树ti 和tj ,将它们合并成一棵新树zk ,新树的左孩子为ti ,右孩子为tj ,zk 的权值为ti 和tj 的权值之和。 (4)从集合T 中删去ti 、tj ,加入zk 。 (5)重复第(3)~(4)步。 (6)约定左分支上的编码为“0”,右分支上的编码为“1”。从叶子节点到根节点逆向求出每个字符的哈夫曼编码。那么从根节点到叶子节点路径上的字符组成的字符串为该叶子节点的哈夫曼编码,算法结束。 \2. 完美图解 假设一些字符及它们的使用频率如下表所示,那么如何得到它们的哈夫曼编码呢? 可以把每一个字符都作为叶子,将它们对应的频率作为其权值,因为只是比较大小,所以为了比较方便,可以对其同时扩大一百倍,得到a:5、b:32、c:18、d:7、e:25、f:13。 (1)初始化。构造n 棵节点为n 个字符的单节点树集合T ={a,b,c,d,e,f},如下图所示。 (2)从集合T 中取出没有双亲且权值最小的两棵树a和d,将它们合并成一棵新树t 1 ,新树的左孩子为a,右孩子为d,新树的权值为a和d的权值之和12。将新树的树根t 1 加入集合T ,将a、d从集合T 中删除,如下图所示。 (3)从集合T 中取出没有双亲且权值最小的两棵树t 1 和f,将它们合并成一棵新树t 2 ,新树的左孩子为t 1 ,右孩子为f,新树的权值为t 1 和f的权值之和25。将新树的树根t 2 加入集合T ,将t 1 和f从集合T 中删除,如下图所示。 (4)从集合T 中取出没有双亲且权值最小的两棵树c和e,将它们合并成一棵新树t 3 ,新树的左孩子为c,右孩子为e,新树的权值为c和e的权值之和43。将新树的树根t 3 加入集合T ,将c和e从集合T 中删除,如下图所示。 (5)从集合T 中取出没有双亲且权值最小的两棵树t 2 和b,将它们合并成一棵新树t 4 ,新树的左孩子为t 2 ,右孩子为b,新树的权值为t 2 和b的权值之和57。新树的树根t 4 加入集合T ,将t 2 和b从集合T 中删除,如下图所示。 (6)从集合T 中取出没有双亲且权值最小的两棵树t 3 和t 4 ,将它们合并成一棵新树t 5 ,新树的左孩子为t 4 ,右孩子为t 3 ,新树的权值为t 3 和t4 的权值之和100。将新树的树根t 5 加入集合T ,将t 3 和t 4 从集合T 中删除,如下图所示。 (7)在集合T 中只剩下一棵树,哈夫曼树构造成功。 (8)约定左分支上的编码为“0”,右分支上的编码为“1”。从叶子节点到根节点逆向求出每个字符的哈夫曼编码。那么从根节点到叶子节点路径上的字符组成的字符串为该叶子节点的哈夫曼编码,如下图所示。 \3. 算法实现 在构造哈夫曼树的过程中,首先将每个节点的双亲、左孩子、右孩子都初始化为-1,找出所有节点中双亲为-1且权值最小的两个节点t 1 、t 2 ,并合并为一棵二叉树,更新信息(双亲节点的权值为t 1 、t 2 权值之和,其左孩子为权值最小的节点t 1 ,右孩子为次小的节点t 2 ,t 1 、t 2 的双亲为双亲节点的编号)。重复此过程,建成一棵哈夫曼树。 (1)数据结构。每个节点的结构都包括权值、双亲、左孩子、右孩子、节点字符信息五个域,如下图所示。 将其定义为结构体形式,定义节点结构体HnodeType。 在结构体的编码过程中,bit[]存放节点的编码,start记录编码开始时的下标,在逆向编码(从叶子到根,想一想为什么不从根到叶子呢?)存储时,start从n -1开始依次递减,从后向前存储;当读取时,从start+1开始到n -1,从前向后输出,即该字符的编码,如下图所示。 编码结构体HcodeType代码如下 2)初始化。初始化哈夫曼树数组HuffNode[]中的节点权值为0,双亲和左、右孩子均为-1,然后读入叶子节点的权值,如下表所示。 (3)循环构造哈夫曼树。从集合T 中取出双亲为-1且权值最小的两棵树ti 和tj ,将它们合并成一棵新树zk ,新树的左孩子为ti ,右孩子为tj ,zk的权值为ti 和tj 的权值之和 完美图解: 第1步,i =0时:j =0; j <6;找双亲为-1且权值最小的两个数。 数据更新后如下表所示。 对应的哈夫曼树如下图所示。 第2步,i =1时:j =0; j <7;找双亲为-1且权值最小的两个数。 对应的哈夫曼树如下图所示。 第3步,i =2时:j =0; j <8;找双亲为-1且权值最小的两个数。 第4步,i =3时:j =0; j <9;找双亲为-1且权值最小的两个数 数据更新后如下表所示。 对应的哈夫曼树如下图所示。 第5步,i =4时:j =0; j <10;找双亲为-1且权值最小的两个数。 数据更新后如下表所示。 对应的哈夫曼树如下图所示。 (4)输出哈夫曼编码。 哈夫曼编码数组如下图所示。 第1步,i =0时:c =0。 构造好的哈夫曼树数组如下表所示。 如果p!=-1,那么从表HuffNode[]中读出节点6的左孩子和右孩子,判断节点0是它的左孩子还是右孩子;如果是左孩子,则编码为0;如果是右孩子,则编码为1。 从上表中可以看出: 哈夫曼树和哈夫曼编码数组如下图所示。 哈夫曼树和哈夫曼编码数组如下图所示。 HuffCode[]数组如下图所示(图中的箭头不表示指针) \4. 算法分析 **时间复杂度:**则该算法时间复杂度为O (n 2 )。 空间复杂度: 所需存储空间为节点结构体数组与编码结构体数组,哈夫曼树数组HuffNode[]中的节点为n 个,每个节点都包含bit[MAXBIT]和start两个域,则该算法的空间复杂度为O (n ×MAXBIT)。 题目描述(POJ3253): 约翰想修牧场周围的篱笆,需要N 块(1≤N ≤20000)木板,每块木板都具有整数长度Li (1≤Li ≤50000)米。他购买了一块足够长的木板(长度为Li 的总和,i =1,2,…, N ),以便得到N 块木板。切割时木屑损失的长度不计。 农夫唐向约翰收取切割费用。切割一块木板的费用与其长度相同。切割长度为21米的木板需要21美分。唐让约翰决定切割木板的顺序和位置。约翰知道以不同的顺序切割木板,将会产生不同的费用。帮助约翰确定他得到N 块木板的最低金额。 输入: 第1行包含一个整数N ,表示木板的数量。第2~N +1行,每行都包含一个所需木板的长度Li 。 输出: 一个整数,即进行N -1次切割的最低花费。 题解: 本题类似哈夫曼树的构造方法,每次都选择两个最小的合并,直到合并为一棵树。每次合并的结果就是切割的费用。使用优先队列(最小值优先)时,每次都弹出两个最小值t 1 、t 2 ,t = t 1 +t 2 ,sum+=t ,将t 入队,继续,直到队空。sum为所需花费。 算法代码: 题目描述(POJ1521): 熵编码是一种数据编码方法,通过对去除“冗余”或“额外”信息的消息进行编码来实现无损数据压缩。为了能够恢复信息,编码字形的位模式不允许作为任何其他编码位模式的前缀,称之为“无前缀可变长度”编码。只允许逐位读取编码的比特流,并且每当遇到表示字形的一组比特时,都可以解码该字形。如果不强制使用无前缀约束,则不可能进行这种解码。 第1个例子,考虑文本“AAAAABCD”,对其使用8位ASCII编码需要64位。如果用“00”对“A”编码,用“01”对“B”编码,用“10”对“C”编码,用“11”对“D”编码,那么只需16位编码,得到的位模式将是“0000000000011011”。不过,这仍然是固定长度的编码;使用的是每个字形两位,而不是八位。既然字形“A”出现的频率更高,那么能用更少的位来编码它吗?实际上可以,但为了保持无前缀编码,其他一些位模式将变得比两位长。最佳编码是将“A”编码为“0”,将“B”编码为“10”,将“C”编码为“110”,将“D”编码为“111”(这显然不是唯一的最佳编码,因为B、C和D的编码可以在不增加最终编码消息大小的情况下自由地交换给任何给定的编码)。使用此编码,消息仅以13位编码到“0000010110111”,压缩比为4.9:1(即最终编码消息中的每一位表示的信息与原始编码中的4.9位表示的信息相同)。从左到右阅读这个位模式,将看到无前缀编码使得将其解码为原始文本变得简单,即使代码的位长度不同。 第2个例子,考虑文本“THE CAT IN THE HAT”。字母“T”和空格字符都以最高频率出现,因此它们在最佳编码中显然具有最短的编码位模式。字母“C”、“I”和“N”只出现一次,因此它们的代码最长。有许多可能的无前缀可变长度位模式集可以产生最佳编码,也就是说,允许文本以最少的位进行编码。其中一种最佳编码是:空格:00、A:100、C:1110、E:1111、H:110、I:1010、N:1011、T:01。因此,这种最佳编码只需51位,与用8位ASCII编码对消息进行编码所需的144位相比,压缩比为2.8:1。 输入: 输入文件包含一个字符串列表,每行一个。字符串将只包含大写字母、数字字符和下画线(用于代替空格)。以字符串“END” 结尾,不应处理此行。 输出: 对于每个字符串,都输出8位ASCII编码的位长度、最佳无前缀可变长度编码的位长度及精确到一个小数点的压缩比。 题解 :本题非常简单,最佳无前缀可变长度编码就是哈夫曼编码。首先根据字符串统计每个字符出现的频率,然后按照频率构造哈夫曼树,计算总的编码长度。 算法代码: 题目描述(UVA12676): 静态哈夫曼编码是一种主要用于文本压缩的编码算法。给定一个由N 个不同字符组成的特定长度的文本,算法选择N 个编码,每个不同的字符都对应一个编码。使用这些编码压缩文本,当选择编码算法构建一个具有N 个叶子的二叉树时,对于N ≥2,树的构建流程如下。 (1)对文本中的每个不同字符,都构建一个仅包含单个节点的树,其权值为该字符在文本中的出现次数。 (2)构建一个包含上述N 棵树的集合S 。 (3)当S 包含多于一棵树时:①选择最小的权值t 1 ∈S ,并将其从S 中删除;②选择最小的权值t 2 ∈S ,并将其从S 中删除;③构建一棵新树t,t 1 为其左子树,t 2 为其右子树,t 的权值为t 1 、t 2 权值之和;④将t 加入S 集合。 (4)返回保留在S 中的唯一一棵树。 对于文本“abracadabra”,由上述过程生成的树,可以像下面左图,其中每个叶子节点内都是该字符在文本中出现的次数(权值)。请注意获得的树不是唯一的,也可以像下面右图或其他,因为可能包含几个权值最小的树。 对文本中的每个不同字符,其编码都取决于最终树中从根到对应字符的叶子之间的路径,编码的长度是这条路径中的边数。假设该算法构建的是左侧的树,“r”的代码长度为3,“d”的代码长度为4。根据算法选择的N 个代码的长度,找所有字符总数的最小值。 输入: 输入包含多个测试用例,每个测试用例的第1行都包含一个整数N (2≤N ≤50),表示在文本中出现的不同字符数。第2行包含N 个整数Li (1≤Li ≤50,i =1,2,…,N ),表示由哈夫曼算法生成的不同字符的编码长度。假设至少存在一棵由上述算法构建的树,那么可以生成具有给定长度的编码。 输出: 对每个测试用例都输出一行,表示所有字符总数的最小值。 题解 :本题不是简单的哈夫曼编码问题,而是反其道而行之,根据编码长度,推测最小字符数。 例如: 其最长编码为3,即最大深度为3。底层节点的权值至少为1,每一层节点的权值至少是下一层节点权值的最大值。如果当前节点的权值比下一层节点的权值小,就会出现在下一层了,因为权值越小,出现的层次越大,如下图所示。 根据编码长度推测,该文本至少有5个字符:1个a、1个d、1个c、2个b。 \1. 算法设计 (1)在每一层都用一个深度数组deep[]记录该层节点的权值,将该层每个节点的权值都初始化为0,等待推测权值。 (2)根据输入的编码长度算出最大长度,即哈夫曼树的最大深度maxd。 (3)从最大深度maxd向上计算并推测,直到树根。开始时temp=1。 i =maxd:第i 层的节点权值如果为0,则被初始化为temp。对第i 层从小到大排序,然后将第i 层每两个合并,将权值放入上一层(i -1层)。更新temp为第i 层排序后的最后一个元素(最大元素)。 i =maxd-1:重复上述操作。 i =0:结束,输出第0层第1个元素。 \2. 算法实现 题目描述(UVA240): 哈夫曼编码是一种最优编码方法。根据已知源字母表中字符的出现频率,将源字母表中的字符编码为目标字母表中的字符,最优的意思是编码信息的平均长度最小。在该问题中,需要将N 个大写字母(源字母S1 …S N 、频率f1 …f N )转换成R 进制数字(目标字母T1 …T R )。 当R =2时,编码过程分几个步骤。在每个步骤中都有两个最低频率的源字母S1 和S2 ,合并成一个新的“组合字母”,频率为S1 和S2 的频率之和。如果最低频率和次低频率相等,则字母表中最早出现的字母被选中。经过一系列步骤后,最后只剩两个字母合并,将每次合并的字母都分配一个目标字符,将较低频率的分配0,将另一个分配1。如果在一次合并中,每个字母都有相同的频率,则将最早出现的分配0。出于比较的目的,组合字母的值为合并中最早出现的字母的值。源字母的最终编码由每次形成的目标字符组成。 目标字符以相反的顺序连接,最终编码序列中的第1个字符为分配给组合字母的最后一个目标字符。下面的两个图展示了R =2的过程。 当R >2时,对每一个步骤都分配R 个字母。由于每个步骤都将R 个字母或组合字母合并为一个组合字母,并且最后一次合并必须合并R 个字母或组合字母,源字母必须包含k ×(R -1)+R 个字母,k为整数。由于N 可能不是很大,因此必须包括适当数量具有0频率的虚拟字母。这些虚拟字母不包含在输出中。进行比较时,虚拟字母晚于字母表中的任何字母。 哈夫曼编码的基本过程与R =2的过程相同。在每次合并中都将具有最低频率的R 个字母合并,形成新的组合字母,其频率等于在组合字母中包括的字母频率的总和。被合并的字母被分配目标字母符号0~R -1。0被分配给具有最低频率的组合中的字母,1被分配给下一个最低频率,等等。如果字母组合中的几个字母具有相同的频率,则字母表中最早出现的字母被分配较小的目标符号,以此类推。 输入: 输入将包含一个或多个数据集,每行一个。每个数据集都包含整数值R (2≤R ≤10)、整数值N (2≤N ≤26)和整数频率f1 …f N ,每个都为1~999。整个输入数据都以R 为0结束,它不被认为是单独的数据集。 输出: 对每个数据集都在单行上显示其编号(编号从1开始按顺序排列)和平均目标符号长度(四舍五入到小数点后两位)。然后显示N 个源字母和相应的哈夫曼代码,每行都有一个字母和代码。在每个测试用例后都打印一个空行。 题解: 本题为可变基哈夫曼编码,普通的哈夫曼编码为二叉树,即R =2。 例如,输入3 4 5 7 8 15,表示基数R =3,字符个数N =4,每个字符的频率为A: 5、B: 7、C: 8、D: 15,构建的哈夫曼树如下图所示。 需要补充一些虚拟字符,使总数满足k ×(R -1)+R ,k 为整数,这样可以保证每个分支节点都有R 个叉。虚拟字符的频率为0,其优先值排在所有字母之后。生成一个组合时,组合节点的频率为所有子节点频率之和,组合节点的优先值为所有子节点中的最小优先值。 \1. 算法设计 (1)先补充虚拟字符,使N =k ×(R -1)+R ,k 为整数,即(N -R )%(R -1)=0。 (2)每个节点都包含frequency、va、id这3个域,分别表示频率、优先值、序号。 (3)定义优先级。频率越小越优先,如果频率相等,则值越小越优先。 (4)将所有节点都加入优先队列。 (5)构建可变基哈夫曼树。 (6)进行可变基哈夫曼编码。 图通常以一个二元组G =<V , E >表示,V 表示节点集,E 表示边集。|V |表示节点集中元素的个数,即节点数,也被称为图G 的阶,例如在n 阶图中有n 个节点。|E |表示边集中元素的个数,即边数。 若图G 中的每条边都是没有方向的,则称之为无向图;若图G 中的每条边都是有方向的,则称之为有向图。在无向图中,每条边都是由两个节点组成的无序对,例如节点v 1和节点v 3 之间的边,记为(v 1 ,v 3 )或(v 3 ,v 1 )。在有向图中,有向边也被称为弧,每条弧都是由两个节点组成的有序对,例如从节点v 1 到节点v 3 的弧,记为<v 1 ,v 3 >,v 1 被称为弧尾,v 3 被称为弧头,如下图所示。 节点的度指与该节点相关联的边数,记为TD(v )。 握手定理: 所有节点的度数之和等于边数的两倍,即 如果在计算度数之和时,每计算一度就画一条小短线,则可以看出每条边都被计算了两次,如下图所示。 在有向图中,节点的度又被分为入度和出度。节点v 的入度是以节点v 为终点的有向边的数量,记为ID(v ),即进来的边数。节点v 的出度是以节点v 为始点的有向边的数量,记为OD(v ),即发出的边数。节点v 的度等于入度加上出度。所有节点的入度之和等于出度之和,又因为所有节点的度数之和等于边的2倍,因此: 图的结构比较复杂,任何两个节点之间都可能有关系。图的存储分为顺序存储和链式存储。顺序存储包括邻接矩阵和边集数组,链式存储包括邻接表、链式前向星、十字链表和邻接多重表。 邻接矩阵通常采用一个一维数组存储图中节点的信息,采用一个二维数组存储图中节点之间的邻接关系。 \1. 邻接矩阵的表示方法 无向图、有向图和网的邻接矩阵的表示方法如下所述。 1)无向图的邻接矩阵 在无向图中,若从节点vi 到节点vj 有边,则邻接矩阵 M [ i ] [ j ] = M [ j ] [ i ] = 1 M [i ][j ]= M[j][i]=1 M[i][j]=M[j][i]=1,否则 M [ i ] [ j ] = 0 M [i][j]=0 M[i][j]=0。 无向图的邻接矩阵的特点如下。 (1)无向图的邻接矩阵是对称矩阵,并且是唯一的。 (2)第i 行或第i 列非零元素的个数正好是第i 个节点的度。上图中的邻接矩阵,第3列非零元素的个数为2,说明第3个节点c 的度为2。 2)有向图的邻接矩阵 在有向图中,若从节点vi 到节点vj 有边,则邻接矩阵 M [ i ] [ j ] = 1 M [i][j]=1 M[i][j]=1,否则 M [ i ] [ j ] = 0 M [i][j]=0 M[i][j]=0。 例如,一个有向图的节点信息和邻接矩阵如下图所示。在该有向图中,从节点a 到节点b 有边,节点a 、b 在一维数组中的存储位置分别为0、1,因此 M [ 0 ] [ 1 ] = 1 M[0][1]=1 M[0][1]=1。有向图中的边是有向边,从节点a 到节点b 有边,从节点b 到节点a 不一定有边,因此有向图的邻接矩阵不一定是对称的。 有向图的邻接矩阵的特点如下。 (1)有向图的邻接矩阵不一定是对称的。 (2)第i 行非零元素的个数正好是第i 个节点的出度,第i 列非零元素的个数正好是第i 个节点的入度。上图中的邻接矩阵,第3行非零元素的个数为2,第3列非零元素的个数也为2,说明第3个节点c 的出度和入度均为2。 3)网的邻接矩阵 网是带权图,需要存储边的权值,则邻接矩阵表示为 Cannot read property 'type' of undefined 例如,一个网的节点信息和邻接矩阵如下图所示。在该网中,从节点a 到节点b 有边,且该边的权值为2,节点a 、b 在一维数组中的存储位置分别为0、1,因此 M [ 0 ] [ 1 ] = 2 M[0][1]=2 M[0][1]=2。从节点b 到节点a 没有边,因此 M [ 1 ] [ 0 ] = ∞ M[1][0]=∞ M[1][0]=∞。 \2. 邻接矩阵的数据结构定义 首先定义邻接矩阵的数据结构,如下图所示。 \3. 邻接矩阵的存储方法 算法步骤: (1)输入节点数和边数; (2)依次输入节点信息,将其存储到节点数组Vex[]中; (3)初始化邻接矩阵,如果是图,则将其初始化为0;如果是网,则将其初始化为∞; (4)依次输入每条边依附的两个节点,如果是网,则还需要输入该边的权值。 • 如果是无向图,则输入a b ,查询节点a、b 在节点数组Vex[]中的存储下标i 、j ,令Edge[i ][j ]=Edge[j ][i ]=1。 • 如果是有向图,则输入a b ,查询节点a、b 在节点数组Vex[]中的存储下标i 、j ,令Edge[i ][j ]=1。 • 如果是无向网,则输入a b w ,查询节点a、b 在节点数组Vex[]中的存储下标i 、j ,令Edge[i ][j ]=Edge[j ][i ]=w 。 • 如果是有向网,则输入a b w ,查询节点a、b 在节点数组Vex[]中的存储下标i 、j ,令Edge[i ][j ]=w 。 完美图解: 一个无向图如下图所示,其邻接矩阵的存储过程如下所述。 (1)输入节点数和边数。 结果:G .vexnum=4、G .edgenum=5。 (2)输入节点信息,将其存入节点信息数组。 存储结果如下图所示。 (3)初始化邻接矩阵的值均为0,如下图所示。 (4)依次输入每条边依附的两个节点。 输入a b ,处理结果:在Vex[]数组中查找到节点a 、b 的下标分别为0、1,是无向图,因此令Edge[0][1]=Edge[1][0]=1,如下图所示。 输入a d ,处理结果:在Vex[]数组中查找到节点a 、d 的下标分别为0、3,是无向图,因此令Edge[0][3]= Edge[3][0]=1,如下图所示。 输入b c ,处理结果:在Vex[]数组中查找到节点b 、c 的下标分别为1、2,是无向图,因此令Edge[1][2]= Edge[2][1]=1,如下图所示。 输入b d ,处理结果:在Vex[]数组中查找到节点b 、d 的下标分别为1、3,是无向图,因此令Edge[1][3]= Edge[3][1]=1,如下图所示。 输入c d ,处理结果:在Vex[]数组中查找到节点c 、d 的下标分别为2、3,是无向图,因此令Edge[2][3]= Edge[3][2]=1,如下图所示。 在实际应用中,也可以先输入节点信息并将其存入数组Vex[]。在输入边时直接输入节点的存储下标序号,这样可以节省查询节点下标所需的时间,从而提高效率。 \4. 邻接矩阵的优缺点 (1)优点如下。 快速判断在两节点之间是否有边。在图中,Edge[i ][j ]=1,表示有边;Edge[i ][j ]=0,表示无边。在网中,Edge[i ][j ]=∞,表示无边,否则表示有边。时间复杂度为O (1)。 方便计算各节点的度。在无向图中,邻接矩阵第i 行元素之和就是节点i 的度;在有向图中,第i 行元素之和就是节点i 的出度,第i 列元素之和就是节点i 的入度。时间复杂度为O (n )。 (2)缺点如下。 不便于增删节点。增删节点时,需要改变邻接矩阵的大小,效率较低。 不便于访问所有邻接点。访问第i 个节点的所有邻接点时,需要访问第i 行的所有元素,时间复杂度为O (n )。访问所有节点的邻接点,时间复杂度为O (n 2 )。 空间复杂度高,为O (n 2 )。 在实际应用中,如果在一个程序中只用到一个图,就可以用一个二维数组表示邻接矩阵,直接输入节点的下标,省去节点信息查询步骤。有时如果图无变化,则为了方便,可以省去输入操作,直接在程序头部定义邻接矩阵。 例如,可以直接定义图的邻接矩阵如下: 边集数组通过数组存储每条边的起点和终点,如果是网,则增加一个权值域。网的边集数组数据结构定义如下: 采用边集数组计算节点的度或查找边时,要遍历整个边集数组,时间复杂度为O (e )。除非特殊需要,很少使用边集数组,例如求解最小生成树kruskal算法时需要按权值对边进行排序,使用边集数组更方便。 邻接表是图的一种链式存储方法,其数据结构包括两部分:节点和邻接点。 \1. 邻接表的表示方法 1)无向图的邻接表 例如,一个无向图及其邻接表如下图所示。一个节点的所有邻接点构成一个单链表。 解释: 节点a 的邻接点是节点b 、d ,其邻接点的存储下标为1、3,按照头插法(逆序)将其放入节点a 后面的单链表中; 节点b 的邻接点是节点a 、c 、d ,其邻接点的存储下标为0、2、3,将其放入节点b 后面的单链表中; 节点c 的邻接点是节点b、d ,其邻接点的存储下标为1、3,将其放入节点c 后面的单链表中; 节点d 的邻接点是节点a、b、c ,其邻接点的存储下标为0、1、2,将其放入节点d 后面的单链表中。 无向图邻接表的特点如下。 如果无向图有n 个节点、e 条边,则节点表有n 个节点,邻接点表有2e 个节点。 节点的度为该节点后面单链表中的节点数。 在上图中,节点数n =4,边数e =5,则在该图的邻接表中,节点表有4个节点,邻接点表有10个节点。节点a 的度为2,其后面单链表中的节点数为2;节点b 的度为3,其后面单链表中的节点数为3。 2)有向图的邻接表(出弧) 例如,一个有向图及其邻接表如下图所示。 解释 节点a 的邻接点(只看出边,即出弧)是节点b、c、e ,其邻接点的存储下标为1、2、4,按照头插法(逆序)将其放入节点a 后面的单链表中; 节点b 的邻接点是节点c ,其邻接点的存储下标为2,将其放入节点b 后面的单链表中; 节点c 的邻接点是节点d、e ,其邻接点的存储下标为3、4,按头插法将其放入节点c 后面的单链表中; 节点d 的邻接点是节点e ,其邻接点的存储下标为4,将其放入节点d 后面的单链表中; 节点e 没有邻接点,其后面的单链表为空。 注意: 对有向图中节点的邻接点,只看该节点的出边(出弧)。 有向图的邻接表的特点如下。 如果有向图有n 个节点、e 条边,则节点表有n 个节点,邻接点表有e 个节点。 节点的出度为该节点后面单链表中的节点数。 在上图中,节点数n =5,边数e =7,则在该图的邻接表中,节点表有5个节点,邻接点表有7个节点。节点a 的出度为3,其后面单链表中的节点数为3;节点c 的出度为2,其后面单链表中的节点数为2。 在有向图邻接表中很容易找到节点的出度,但是找入度很难,需要遍历所有邻接点表中的节点,查找到该节点出现了多少次,入度就是多少。例如在下图中,节点c 的下标为2,在邻接点表中有两个为2的节点,因此节点c 的入度为2;节点e 的下标为4,在邻接点表中有3个为4的节点,因此节点e 的入度为3。 3)有向图的逆邻接表(入弧) 有时为了方便得到节点的入度,可以建立一个有向图的逆邻接表,如下图所示。 解释: • 节点a 没有逆邻接点(只看入边,即入弧),其后面的单链表为空; • 节点b 的逆邻接点是节点a ,其邻接点的存储下标为0,将其放入节点b 后面的单链表中; • 节点c 的逆邻接点是a、b ,其邻接点的存储下标为0、1,按照头插法将其放入节点c 后面的单链表中; • 节点d 的逆邻接点是节点c ,其邻接点的存储下标为2,将其放入节点d 后面的单链表中; • 节点e 的逆邻接点是节点a、c、d ,其邻接点的存储下标为0、2、3,按照头插法(逆序)将其放入节点e 后面的单链表中。 注意: 对有向图中节点的逆邻接点,只看该节点的入边(入弧)。 有向图的逆邻接表的特点如下。 (1)如果有向图有n 个节点、e 条边,则节点表有n 个节点,邻接点表有e 个节点。 (2)节点的入度为该节点后面的单链表中的节点数。 在上图中,节点数n =5,边数e =7,在该图的邻接表中,节点表有5个节点,邻接点表有7个节点。节点a 的入度为其后面的单链表中的节点数0,节点c 的入度为其后面的单链表中的节点数2。 \2. 邻接表的数据结构定义 邻接表的数据结构包括节点和邻接点,对其分别定义如下。 (1)节点。包括节点信息data和指向第1个邻接点的指针first,如下图所示。 (2)邻接点。包括该邻接点的存储下标v 和指向下一个邻接点的指针next,如果是网的邻接点,则还需增加一个权值域w ,如下图所示。 邻接表的结构体定义,如下图所示。 邻接表的存储方法 算法步骤: (1)输入节点数和边数; (2)依次输入节点信息,将其存储到节点数组Vex[]的data域中,将Vex[]的first域置空; (3)依次输入每条边依附的两个节点,如果是网,则还需要输入该边的权值。 • 如果是无向图,则输入a b ,查询节点a、b 在节点数组Vex[]中的存储下标i 、j ,创建一个新的邻接点s ,令s ->v =j ; s ->next=NULL;然后将节点s 插入第i 个节点的第1个邻接点之前(头插法)。在无向图中,从节点a 到节点b 有边,从节点b 到节点a 也有边,因此还需要创建一个新的邻接点s 2 ,令s 2 ->v =i ; s2 ->next=NULL;然后将s 2 节点插入第j 个节点的第1个邻接点之前(头插法)。 • 如果是有向图,则输入a b ,查询节点a、b 在节点数组Vex[]中的存储下标i 、j ,创建一个新的邻接点s ,令s ->v =j ; s ->next=NULL;将节点s 插入第i 个节点的第1个邻接点之前(头插法)。 • 如果是无向网或有向网,则和无向图或有向图的处理方式一样,只是邻接点多了一个权值域。 完美图解: 一个有向图如下图所示,其邻接表的存储过程如下所述。 (1)输入节点数5和边数7,G .vexnum=5,G .edgenum=7。 (2)输入节点信息a b c d e 并将其存入节点表,存储结果如下图所示。 (3)依次输入每条边依附的两个节点。 输入a b ,处理结果:在Vex[]数组的data域中查找到节点a 、b 的下标分别为0、1,创建一个新的邻接点s ,令s ->v =1; s ->next=NULL。将节点s 插入第0个节点的第1个邻接点之前(头插法)。 • 输入a c ,处理结果:在Vex[]数组的data域中查找到节点a 、c 的下标分别为0、2,创建一个新的邻接点s ,令s ->v=2; s ->next=NULL。将节点s 插入第0个节点的第1个邻接点之前(头插法)。 • 输入a e ,处理结果:在Vex[]数组的data域中查找到节点a 、e 的下标分别为0、4,创建一个新的邻接点s ,令s ->v =4; s ->next=NULL。将节点s 插入第0个节点的第1个邻接点之前(头插法)。 • 输入b c ,处理结果:在Vex[]数组的data域中查找到节点b 、c 的下标分别为1、2,创建一个新的邻接点s ,令s ->v =2; s ->next=NULL。将节点s 插入第1个节点的第1个邻接点之前(头插法)。 • 输入c d ,处理结果:在Vex[]数组的data域中查找到节点c 、d 的下标分别为2、3,创建一个新的邻接点s ,令s ->v =3; s ->next=NULL。将节点s 插入第2个节点的第1个邻接点之前(头插法)。 • 输入c e ,处理结果:在Vex[]数组的data域中查找到c 、e 的下标分别为2、4,创建一个新的邻接点s ,令s ->v =4; s ->next=NULL。将节点s 插入第2个节点的第1个邻接点之前(头插法)。 • 输入d e ,处理结果:在Vex[]数组的data域中查找到节点d 、e 的下标分别为3、4,创建一个新的邻接点s ,令s ->v =4; s ->next=NULL。将节点s 插入第3个节点的第1个邻接点之前(头插法)。 注意: 由于后输入的内容被插在了单链表的前面,因此若输入顺序不同,则建立的单链表也不同。 算法代码: \4. 邻接表的优缺点 (1)优点如下。 • 便于增删节点。 • 便于访问所有邻接点。访问所有节点的邻接点,其时间复杂度为O (n +e )。 • 空间复杂度低。节点表占用n 个空间,无向图的邻接点表占用n +2e 个空间,有向图的邻接点表占用n +e 个空间,总体空间复杂度为O (n +e )。而邻接矩阵的空间复杂度为O ( n 2 n^2 n2 )。因此,对于稀疏图,可采用邻接表存储;对于稠密图,可采用邻接矩阵存储。 (2)缺点如下。 • 不便于判断在两个节点之间是否有边。要判断在两个节点之间是否有边,需要遍历该节点后面的邻接点链表。 • 不便于计算各节点的度。在无向图邻接表中,节点的度为该节点后面单链表中的节点数;在有向图邻接表中,节点的出度为该节点后面单链表中的节点数,但不易于求入度;在有向图的逆邻接表中,节点的入度为该节点后面单链表中的节点数,但不易于求出度。 虽然以邻接表访问单条边的效率不高,但是访问同一节点的所有关联边时,仅需访问该节点后面的单链表,时间复杂度为该节点的度O (d (vi ));而以邻接矩阵访问同一节点的所有关联边时,时间复杂度为O (n)。总体上,邻接表比邻接矩阵效率更高。 链式前向星采用了一种静态链表存储方式,将边集数组和邻接表相结合,可以快速访问一个节点的所有邻接点,在算法竞赛中被广泛应用。 链式前向星有如下两种存储结构。 (1)边集数组:edge[],edge[i ]表示第i 条边。 (2)头节点数组:head[],head[i ]存储以i 为起点的第1条边的下标(edge[]中的下标)。 按以下顺序输入每条边的两个端点,建立链式前向星,过程如下。 (1)输入1 2 5。创建一条边1-2,权值为5,创建第1条边edge[0],将该边链接到节点1的头节点中(初始时head[]数组全部被初始化为-1)。即edge[0].next=head[1]; head[1]=0,表示节点1关联的第1条边为0号边,如下图所示。图中的虚线箭头仅表示它们之间的链接关系,不是指针。 因为是无向图,所以还需添加它的反向边2-1,权值为5。创建第2条边edge[1],将该边链接到节点2的头节点中。即edge[1].next=head[2]; head[2]=1;表示节点2关联的第1条边为1号边,如下图所示。 (2)输入1 4 3。创建一条边1-4,权值为3。创建第3条边edge[2],将该边链接到节点1的头节点中(头插法)。即edge[2].next=head[1]; head[1]=2,表示节点1关联的第1条边为2号边,如下图所示。 因为是无向图,所以还需要添加它的反向边4-1,权值为3。创建第4条边edge[3],将该边链接到节点4的头节点中。即edge[3].next=head[4]; head[4]=3,表示节点4关联的第1条边为3号边,如下图所示。 (3)依次输入三条边2 3 8、2 4 12、3 4 9,创建的链式前向星如下图所示。 添加一条边u v w 的代码如下: 如果是有向图,则每输入一条边,都执行一次add(u ,v ,w )即可;如果是无向图,则需要添加两条边add(u ,v ,w ); add(v ,u ,w )。 如何使用链式前向星访问一个节点u 的所有邻接点呢?代码如下。 链式前向星的特性如下。 (1)和邻接表一样,因为采用头插法进行链接,所以边的输入顺序不同,创建的链式前向星也不同。 (2)对于无向图,每输入一条边,都需要添加两条边,互为反向边。例如,输入第1条边1 2 5,实际上添加了两条边,如下图所示。这两条边互为反向边,可以通过与1的异或运算得到其反向边,01=1,11=0。也就是说,如果一条边的下标为i ,则其反向边为i ^1。这个特性在网络流中应用起来非常方便。 (3)链式前向星具有边集数组和邻接表的功能,属于静态链表,不需要频繁地创建节点,应用起来十分灵活。 题目描述(P3916): 给定有N 个节点、M 条边的有向图,对每个节点v 都求A (v ),表示从节点v 出发,能到达的编号最大的节点。 输入: 第1行包含两个整数N 、M (1≤N ,M ≤105 )。接下来的M 行,每行都包含两个整数Ui 、Vi,表示边(Ui ,Vi )。节点的编号为1~N 。 输出: N 个整数A(1),A(2),⋯,A(N )。 题解: 本题求从节点v 出发能遍历到的最大节点,可以采用以下两种思路。 • 从节点v 出发,深度优先遍历所有的节点,求最大值。 • 也可以换种思路,建立原图的反向图,从最大节点u 出发,对凡是能遍历到的节点v ,v 能到达的编号最大的节点就是u 。如下图所示,在反向图中,节点4能遍历到的节点是4、1、2,这3个节点能到达的最大编号节点都是4;节点3能遍历到的节点是3、4,但是节点4已经有解,无须求解,因此节点3能到达的最大节点是3。 \1. 算法设计 (1)存储图的反向图。 (2)在反向图上进行倒序深度遍历。 \2. 算法实现 题目描述(UVA11175): 有向图D有n 个节点和m 条边,可以通过以下方式制作D的Lying图E。E将有m 个节点,每个都用于表示D的每条边。例如,如果D具有边(u ,v ),则E将具有节点uv。现在,当D具有边(u ,v )和(v ,w )时,E将具有从节点uv到节点vw的边。在E中没有其他边。给定一个图E,确定E是否可能是某个有向图D的Lying图。注意,在D中允许有重复的边和自环。 输入: 第1行包含测试用例数N (N <220)。在每个测试用例的前两行都包含m (0≤m ≤300)和k,表示图E中的节点数和边数。下面的k 行,每行都包含两个节点x 和y ,表示在E中从x 到y 有一条边。节点编号为0~m -1。 输出: 对每个测试用例,都输出一行Case #t :,其中t 表示测试用例编号,然后是Yes或者No,用于判断E是否是一个有向图D的Lying图。 题解: 本题实际上就是把D中的边缩成点,D中的一条边对应E中的一个节点,如果在D中存在边i (u ,v)和j (v ,w ),则E将具有从节点i 到节点j 的边。 如果在D中边i 和边j 有公共端点,则i 连接的边,j 一定也连接,不存在i 连接的边但是j 没连接的情况。那么在E中,节点i 和节点j 有公共邻接点,则i 邻接的节点,j 一定也邻接。如下图所示,在D中,边i 和边j有公共端点c ,i 连接边k 1 、k 2 ,j 则一定也连接边k 1 、k 2 ;在对应的E中,节点i 和节点j 有公共邻接点k1 ,i 有邻接点k 2 ,j 则一定也有邻接点k 2 。 (1)用邻接矩阵存储E。 (2)判断在E中是否存在节点i 和节点j 有公共邻接点但是对i 邻接的节点而j 不邻接的情况。 题目描述(POJ3275): 约翰想按照奶牛的产奶能力给它们排序。已知有N (1≤N ≤1 000)头奶牛,而且知道这些奶牛的M (1≤M ≤10 000)种关系,将每种关系都表示为“X Y ”,表示奶牛X 的产奶能力大于奶牛Y 。约翰想知道自己至少还要调查多少对关系才能完成整个排序。 输入: 第1行包含两个整数N 和M 。第2…M +1行,每行都包含两个整数X 和Y 。X 和Y 都在1~N 范围内,表示奶牛X 的排名高于奶牛Y 。 输出: 单行输出至少还要调查多少种关系才能完成整个排序。 提示: 在输入样例中,cow2 >cow1 >cow5 ,cow2 >cow3 >cow4 ,所以cow2 的排名最高。不过,约翰需要知道排名大于cow1 及cow3 的排名第二的牛,还需要通过一个问题来确定cow4 和cow5 的顺序。之后,他需要知道如果cow1 大于cow3 ,那么cow5 是否大于cow3 。他必须问三个问题才能确定排名:“cow1>cow3 ?cow4 >cow5 ?”“cow5 >cow3 ?”。 题解: (2)根据传递性,得到的已知关系有7种,分别是:1>4、1>5、2>1、2>3、2>4、2>5、3>4。 (3)对于有n 个节点的图,两两之间的关系一共有n (n -1)/2种,5个节点共有5×4/2=10种关系,还需要知道10-7=3种关系即可。 如何得到已知关系呢?可以利用bitset位运算,将每个节点都用一个bitset来表示。 初始化时,p [i ][i ]=1,即p [i ]的第i 位为1(从右侧数第0位、1位、2位)。 输入1-5,令p [1][5]=1,则p [1]=…….100010。 输入1-4,令p [1][4]=1,则p [1]=…….110010。 输入2-1,令p [2][1]=1,则p [2]=…….000110。 输入2-3,令p [2][3]=1,则p [2]=…….001110。 输入3-4,令p [3][4]=1,则p [3]=…….011000。 判断每个数组的每一位,代码如下。 例如,p [2][1]=1,则p [2]=p [2]|p [1]= 001110 | 110010=111110。如果2和1有关系,而1和4、5有关系,则通过或运算,可以得出2和4、5也有关系。 通过此方法,可以找到每个点和其他点的关系。用ans累计每个数组元素1的个数,因为初始化时自己到自己为1,所以ans多算了n 种关系,已知关系数应为ans-n ,用n (n -1)/2减去已知关系数即可。 与树的遍历类似,图的遍历指从图的某一节点出发,按照某种搜索方式对图中的所有节点都仅访问一次。图的遍历可以解决很多搜索问题,实际应用非常广泛。图的遍历根据搜索方式的不同,分为广度优先遍历和深度优先遍历。 广度优先搜索(Breadth First Search,BFS)又被称为宽度优先搜索,是最常见的图搜索方法之一。广度优先搜索指从某个节点(源点)出发,一次性访问所有未被访问的邻接点,再依次从这些已访问过的邻接点出发,一层一层地访问。如下图所示,广度优先遍历是按照广度优先搜索的方式对图进行遍历的。 假设源点为1,从1出发访问1的邻接点2、3,从2出发访问4,从3出发访问5,从4出发访问6,访问完毕。访问路径如下图所示。 广度优先遍历的秘籍:先被访问的节点,其邻接点先被访问。 根据广度优先遍历的秘籍,先来先服务,这可以借助于队列实现。因为对每个节点只访问一次,所以可以设置一个辅助数组visited[i ]=false,表示第i 个节点未被访问;visited[i ]=true,表示第i 个节点已被访问。 \1. 算法步骤 (1)初始化所有节点均未被访问,并初始化一个空队列。 (2)从图中的某个节点v 出发,访问v 并标记其已被访问,将v 入队 (3)如果队列非空,则继续执行,否则算法结束。 (4)将队头元素v 出队,依次访问v 的所有未被访问的邻接点,标记已被访问并入队。转向步骤3。 \2. 完美图解 (1)初始化所有节点均未被访问,visited[i ]=false,i =1,2,…,6。并初始化一个空队列Q 。 (2)从节点1出发,标记其已被访问,visited[1]=true,将节点1入队。 (3)将队头元素1出队,依次访问1的所有未被访问的邻接点2、3,标记其已被访问并将其入队。 (4)将队头元素2出队,将2的未被访问的邻接点4标记为已被访问,并将其入队。 (5)将队头元素3出队,3的邻接点2已被访问,将未被访问的邻接点5标记为已被访问,并将其入队。 (6)将队头元素4出队,4的邻接点3已被访问,将未被访问的邻接点6标记为已被访问,并将其入队。 (7)将队头元素5出队,5的邻接点4、6均已被访问,没有未被访问的邻接点。 (8)将队头元素6出队,6没有邻接点。 (9)队列为空,算法结束。广度优先遍历序列为1 2 3 4 5 6。 广度优先遍历经过的节点及边,被称为广度优先生成树。如果广度优先遍历非连通图,则每一个连通分量都会产生一棵广度优先生成树。 算法实现 (1)基于邻接矩阵的广度优先遍历。层次遍历
bool Leveltraverse(Btree T)
{
Btree p;
if(!T)
return false;
queue<Btree>Q;//创建一个普通队列《先进先出),里面存放指针类型
Q.push(T);//根指针入队
while(!Q.empty()) //如果队列不空
{
p=Q.front();//取出队头元素作为当前节点
Q.pop();//队头元素出队
cout<<p->data<<" ";
if(p->lchild)
Q.push(p->lchild); //左孩子指针入队
if(p->rchild)
Q.push(p->rchild); //右孩子指针入队
}
return 0;
}
5.3.5 遍历序列还原树
![]()
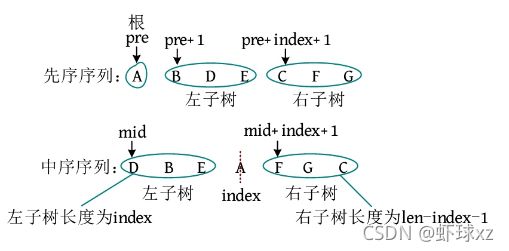
BiTree pre_mid_createBiTree(char *pre,char *mid,int len) //由先序、中序还原建立二叉树
{
if(len == 0)
return NULL;
char ch = pre[0]; //先序序列中的第 1 个节点,作为根
int index = 0;//在中序序列中查找根节点,并用 index 记录查找长度
while(mid[index]!=ch)//在中序序列中查找根节点,左边为该节点的左子树,右边为右子树
index++;
BiTree T = new BiTNode;//创建根节点
T->data=ch;
T->lchild=pre_mid_createBiTree(pre + 1,mid,index);//创建左子树
T->rchild=pre_mid_createBiTree(pre + index + 1,mid + index + 1, len - index - 1);//创建右子树
return T;
}
BiTree pre_mid_createBiTree(char *pre,char *mid,int len) //由先序、中序还原建立二叉树
BiTree pro_mid_createBiTree(char *last, char *mid,int len)//由后序、中序还原建立二又树
{
if(len == 0)
return NULL;
char ch = last[len - 1];//找到后序序列中的最后一个节点,作为根
int index = 0;//亨序列中查找根节点,并用 index 记录查找长度
while(mid[index]!=ch)//在中序序列中找根节点,左边为该节点的左子树,右边为右子树
index++;
BiTree T = new BiTNode; //创建根节点
T->data=ch;
T->lchild=pro_mid_createBiTree(last,mid,index);//创建左子树
T->rchild=pro_mid_createBiTree(last+index,mid+index+1,len-index-1);//创建右子树
return T;
}
训练1 新二叉树
#include 训练2 还原树
#include 训练3 树
#include哈夫曼树
原理 哈夫曼编码
A:0 B:1 C:01 D:10
![]()
typedef struct
{
double weight; //权值
int parent; //双亲
int lchild;//左孩子
int rchild;//右孩子
char value;//该节点表示的字符
}HNodeType;
typedef struct
{
int bit[MAXBIT];//存储编码的数组
int start;//编码开始下标
}
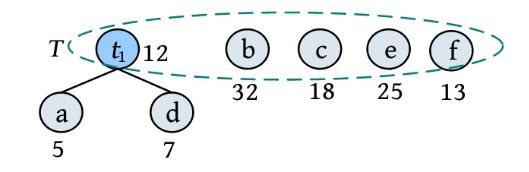
void HuffmanTree(HNodeType HuffCode[MAXNODE],int n)
{
/* i、j: 循环变量,m1、m2:构造哈夫曼树不同过程中两个最小权值结点的权值,
x1、x2:构造哈夫曼树不同过程中两个最小权值结点在数组中的序号。*/
int i,j,x1,x2;
double m1,m2;
/* 初始化存放哈夫曼树数组 HuffNode[] 中的结点 */
for(i = 0;i<2*n-1;i++)
{
HuffNode[i].weight = 0;//权值
HuffNode[i].parent = -1;
HuffNode[i].lchild = -1;
HuffNode[i].rchild = -1;
}
/* 输入 n 个叶子结点的权值 */
for(i = 0;i < n;i++)
{
cout<<"Please input value and weight of leaf node "<<i + 1<<endl;
cin>>HuffCode[i].value>>HuffCode[i].weight;
}
/* 构造 Huffman 树 */
for(i=0;i<n-1;i++)
{
//执行n-1次合并
m1 = m2 = MAXVALUE;
/* m1、m2中存放两个无父结点且结点权值最小的两个结点 */
x1 = x2 = 0;
/* 找出所有结点中权值最小、无父结点的两个结点,并合并之为一棵二叉树 */
for(j = 0;j < n +i;j++)
{
if(HuffNode[j].weight < m1 && HuffNode[j].parent == -1)
{
m2 = m1;
x2 = x1;
m1 = HuffNode[j].weight;
x1 = j;
}
else if(HuffNode[j].weight < m2 && HuffNode[j].parent == -1)
{
m2 = HuffNode[j].weight;
x2 = j;
}
}
/* 设置找到的两个子结点 x1、x2 的父结点信息 */
HuffNode[x1].parent = n + i;
HuffNode[x2].parent = n + i;
HuffNode[n + i].weight = m1 + m2;
HuffNode[n + i].lchild = x1;
HuffNode[n + i].rchild = x2;
cout << "x1.weight and x2.weight in round " << i + 1 << "\t" << HuffNode[x1].weight << "\t" << HuffNode[x2].weight << endl; /* 用于测试 */
}
}
x1=0,x2=3; //x1、x2 为两个最小权值节点的序号
m1=5, m2=7; //ml、m2 为两个最小权值节点的权值
HuffNode[0].parent=6; //xl 的父亲为新节点编号 n+i
HuffNode[3].parent=6; //x2 的父亲为新节点编号 n+i
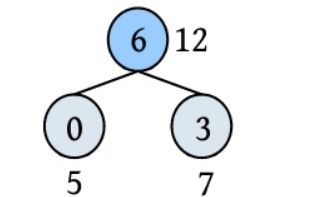
HuffNode[6].weight=12; //新节点权值为两个最小权值之和 ml+m2
HuffNode[6].lchild=0; //新节点n+i 的左孩子为 x1
HuffNode[6].rchild=3; //新节点n+i 的右孩子为 x2
x1=6,x2=5; //xl、x2 为两个最小权值节点的序号
m1=12,m2=13; //ml、m2 为两个最小权值节点的权值
HuffNode[5].parent=7; //xl 的父亲为新节点编号 n+i
HuffNode[6].parent=7; //x2 的父亲为新节点编号 n+i
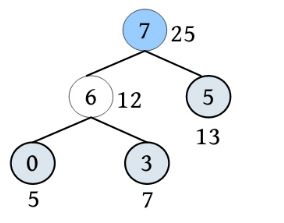
HuffNode[7].weight=25; //新节点权值为两个最小权值之和 ml+m2
HuffNode[7].lchild=6; //新节点 n+i 的左孩子为 x1
HuffNode[7].rchild=5; //新节点 n+i 的右孩子为 x2
x1=2, x2=4; //x1、x2 为两个最小权值节点的序号
m1=18 m2=25; //m1、m2 为两个最小权值节点的权值
HuffNode[2].parent=8; //x1 的父亲为新节点编号 n+i
HuffNode[4].parent=8; //x2 的父亲为新节点编号 n+i
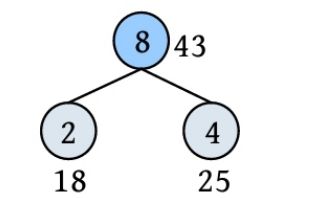
HuffNode[8].weight=43; //新节点权值为两个最小权值之和 m1+m2
HuffNode[8].1child=2; //新节点 n+i 的左孩子为x1
HuffNode[8].rchild=4; //新节点 n+i 的右孩子为x2
x1=7,x2=1; //x11、x2 为两个最小权值节点的序号
m1=25, m2=32; //m1、m2 为两个最小权值节点的权值
HuffNode[7].parent=9; //x1 的父亲为新节点编号 n+i
HuffNode[1].Parent=9; //x2 的父亲为新节点编号 n+i
HuffNode[9].weight=57; //新节点权值为两个最小权值之和 m1+m2
HuffNode[9].lchild=7; //新节点 n+i 的左孩子为 x1
HuffNode[9].xchild=17 //新节点 nt+i 的右孩子为x2
x1=8,x2=9; //x1、x2 为两个最小权值节点的序号
m1=43, m2=57; //m1、m2 为两个最小权值节点的权值
HuffNode[8].parent=10; //xl 的父亲为生成的新节点编号 n+i
HuffNode[9].parent=10; //x2 的父亲为生成的新节点编号 n+i
HuffNode[10].weight=100; //新节点权值为两个最小权值之和 ml +tm2
HuffNode[10].lchild=8; //新节点编号 n+i 的左孩子为x1
HuffNode[10].rchild=9; //新节点编号 n+i 的右孩子为x2
/* 哈夫曼树编码 */
void HuffmanCode(HCodeType HuffCode[MAXLEAF],int n)
{
HCodeType cd; /* 定义一个临时变量来存放求解编码时的信息 */
int i,j,c,p;
for(i = 0;i < n;i++)
{
cd.start = n - 1;
c = i;
p = HuffNode[c].parent;
while(p != -1)
{
if(HuffNode[p].lchild == c)
cd.bit[cd.start] = 0;
else
cd.bit[cd.start] = 1;
cd.start--;/*前移一位 */
c = p;
p = HuffNode[c].parent; /* 设置下一循环条件 */
}
/* 把叶子结点的编码信息从临时编码cd中复制出来,放入编码结构体数组 */
for(j = cd.start + 1;j < n;j++)
HuffCode[i].bit[j] = cd.bit[j];
HuffNode[i].start = cd.start;
}
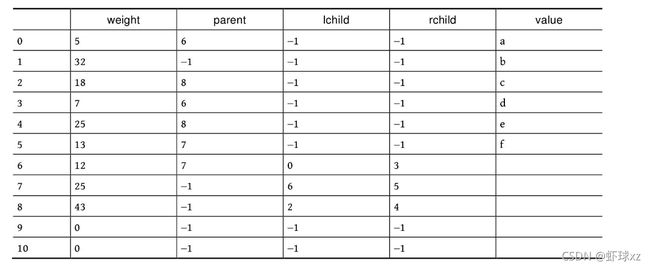
}
cd.start=n-1=5
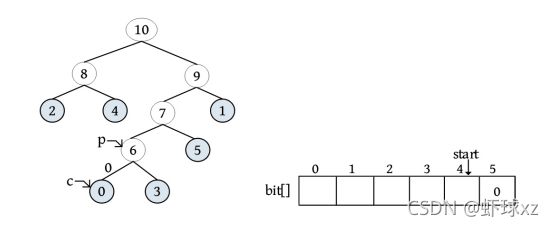
p=HuffNode[0].parent=6;//从哈夫曼树建成后的表 BuffNode [] 中读出,Pp 指向 0 号节点的父亲 6 号
HuffNode[6].lchild=0;// 节点 0 是其父亲节点 6 的左孩子
cd.bit[5] = 0;//编码为 0
cd.start--=4;/* start 向前移动一位*/
c=p=6;/* c、Pp 变量上移,准备下一循环 */
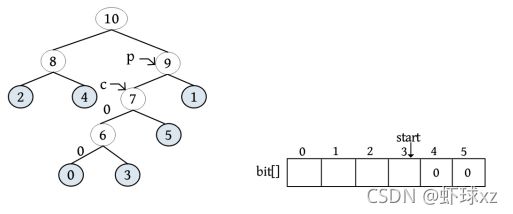
p=HuffNode[6].parent=7;
p!=-1;
HuffNode[7].lchild=6;// 节点6是其父亲节点 7 的左孩子
cd.bit[4]=0; //编码为0
cd.start--=3; /* start 向前移动一位*/
c=p=7;/* c、P 变量上移,准备下一循环 */
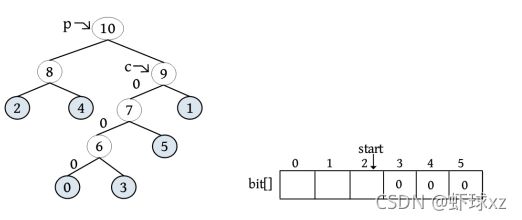
p=HuffNode[7].parent=9;
P!=-1;
HuffNode[9].1child=7;// 节点7是其父亲节点 9 的左孩子
cd.bit[3]=0;//编码为0
cd.start--=2; /* start 向前移动一位*/
C=P=9; /* c、P 变量上移,准备下一循环 */
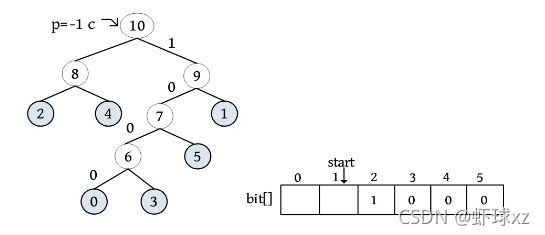
P=HuffNode[9].Parent=10;
p!=-1;
HuffNode[10].1child!=9;// 节点7是其父亲节点 9 的左孩子
cd.bit[2]=1;//编码为1
cd.start--=1; /* start 向前移动一位*/
c=p=10; /* c、P 变量上移,准备下一循环 */
P=HuffNode[10].Parent=-1;
p=-1; 该叶子节点编码结束
/* 把叶子节点的编码信息从临时编码 ca 中复制出来,放入编码结构体数组 */
for (j=cd.start+1; j<n; j++)
HuffCode[i].bit[j]=cd.bit[j],
HuffCode[i].start=cd.start;
训练1 围栏修复
#include 训练2 信息熵
#include训练3 转换哈夫曼编码
4 //表示 4 个不同字符
3 1 2 3 //每个字符编码长度
#include 训练4 可变基哈夫曼编码

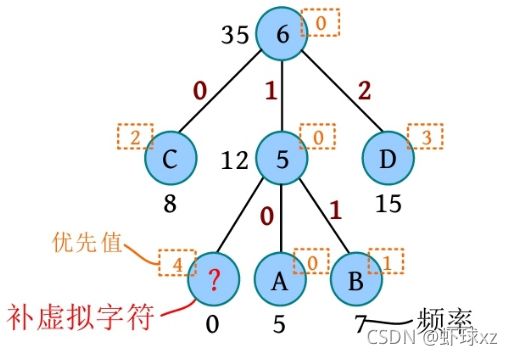
#include图论基础
∑ i = 1 n T D ( v i ) = 2 e \sum^n_{i=1}TD(v_i)=2e i=1∑nTD(vi)=2e
其中,n 为节点数,e 为边数。
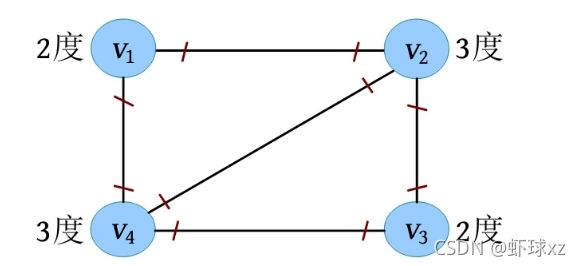
∑ i = 1 n ( v i ) = ∑ i = 1 n O D ( v i ) = e \sum^n_{i=1}(v_i)=\sum^n_{i=1}OD(v_i)=e i=1∑n(vi)=i=1∑nOD(vi)=e图的存储
邻接矩阵
Cannot read property 'type' of undefined
例如,一个无向图的节点信息和邻接矩阵如下图所示。在该无向图中,从节点a 到节点b 有边,从节点b 到节点a 也有边,节点a 、b 在一维数组中的存储位置分别为0、1,则 M [ 0 ] [ 1 ] = M [ 1 ] [ 0 ] = 1 M[0][1]=M[1][0]=1 M[0][1]=M[1][0]=1。
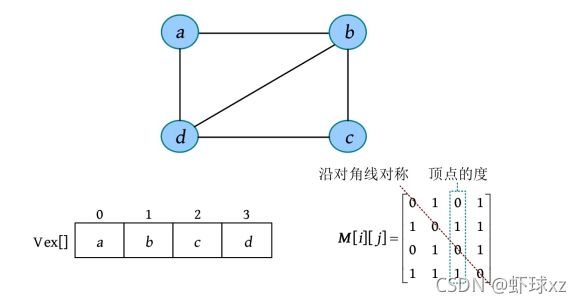
Cannot read property 'type' of undefined
注意: 以尖括号<vi ,vj >表示的是有序对,以圆括号(vi ,vj )表示的是无序对,后同。
其中,wij 表示边上的权值,∞表示无穷大。当i =j 时,wii 也可被设置为0。

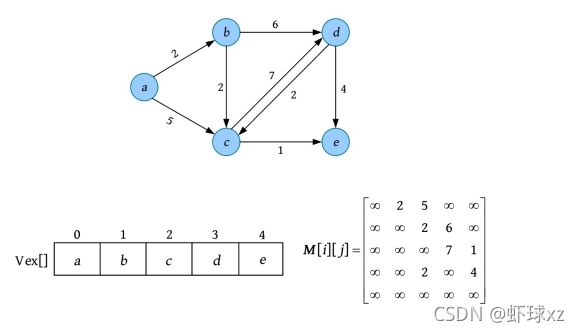
#define MaxVnum 100 //节点数的最大值
typedef char VexType; //节点的数据类型,根据需要定义
typedef int EdgeType;//边上权值的数据类型,若为不带权值的图,则为 0或1
4 5
a b c d
void CreateAMGraph(AMGraph &G)
{
int i,j;
VexType u,v;
cout<<"请输入顶点数:"<<endl;
cin>>G.vexnum;
cout<<"请输入边数: "<<endl;
cin>>G.edgenum;
cout<<"请输入顶点信息:"<<endl;
for(int i = 0;i<G.vexnum;i++) //输入顶点信息,存入顶点信息数组
{
cin>>G.vex[i];
}
for(int i = 0;i<G.vexnum;i++) //初始化邻接矩阵所有值为0,如果是网,则初始化邻接矩阵为无穷大
{
for(int j = 0;j<G.vexnum;j++)
G.Edge[i][j] = 0;
}
cout << "请输入每条边依附的两个顶点:" << endl;
while(G.edgenum--)
{
cin>>u>>v;
i = locatevex(G,u);//查找顶点u的存储下标
j = locatevex(G,v);//查找顶点v的存储下标
if(i != -1 && j != -1)
G.Edge[i][j] = G.Edge[j][i] = 1;//邻接矩阵储置1
else
{
cout << "输入顶点信息错!请重新输入!" << endl;
G.edgenum++;//本次输入不算
}
}
}
i n t M [ m ] [ n ] = { { 0 , 1 , 0 , 1 } , { 1 , 0 , 1 , 1 } , { 0 , 1 , 0 , 1 } , { 1 , 1 , 1 , 0 } } int M[m][n] = \{\{0,1,0,1\},\{1,0,1,1\},\{0,1,0,1\},\{1,1,1,0\}\} intM[m][n]={{0,1,0,1},{1,0,1,1},{0,1,0,1},{1,1,1,0}}边集数组
struct Edge
{
int u;
int v;
int w;
}e[N*N];
邻接表
typedef struct VexNode //定义顶点类型
{
VexType data; // VexType为顶点的数据类型,根据需要定义
AdjNode *first;//指向第一个邻接点
}VexNode;
typedef struct AdjNode //定义邻接点类型
{
int v;//邻接点下标
struct AdjNode *next;//指向下一个邻接点
}AdjNode;
typedef struct //定义邻接表类型
{
VexNode Vex[MaxVnum];
int vexnum,edgenum;//顶点数,边数
}ALGraph;
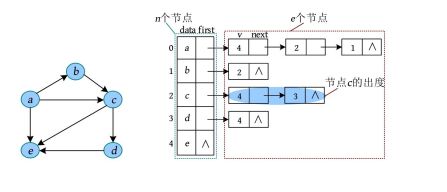
![]()
![]()
void CreateALGraph(ALGraph &G) //创建有向图邻接表
{
int i,j;
VexType u,v;
cout<<"请输入顶点数和边数:"<<endl;
cin>>G.vexnum<<G.edgenum;
cout<<"请输入顶点信息:"<<endl;
for(int i = 0;i<G.vexnum;i++) //输入顶点信息,存入顶点信息数组
cin>>G.vex[i].data;
for(i = 0;i < G.vexnum;i++)
G.vex[i].first = NULL;
cout<<"请依次输入每条边的两个顶点u,v"<<endl;
while(G.edgenum--)
{
cin >> u >> v;
i = locatevex(G, u); //查找顶点u的存储下标
j = locatevex(G, v); //查找顶点v的存储下标
if(i!=-1 && j!=-1)
insertedge(G, i, j);
else
{
cout<<"输入顶点信息错!请重新输入!"<<endl;
G.edgenum++;//本次输入不算
}
}
}
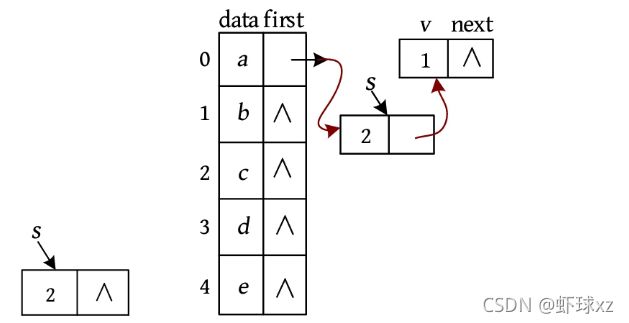
void insertedge(ALGraph &G,int i,int j)//插入一条边
{
AdjNode *s;
s = new AdjNode;
s->v = j;
s->next = G.Vex[i].first;
G.Vex[i].first = s;
}
链式前向星
struct Edge
{
int to,w,next; //边集数组,对边数一般要设置比 maxnxmaxn 大的数,题目有要求除外
}a[maxn];
int headp[maxn];//头节点数组

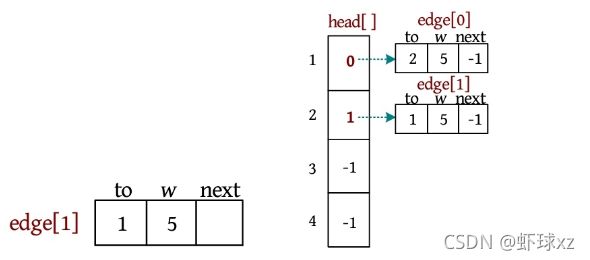

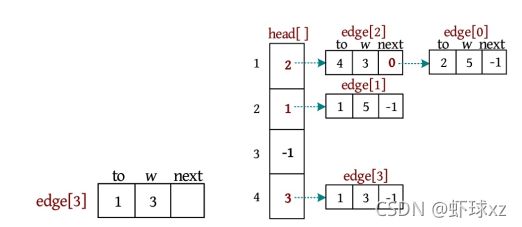

void add(int u,int v,int w) //添加一条边u--v
{
e[cnt].to = v;
e[cnt].w = w;
e[cnt].next = head[u];
head[u] = cnt++;
}
for(int i = head[u];i!=-1;i=edge[i].next) //i!=-1
{
int v = edge[i].to;//
int w = edge[i].w;
}
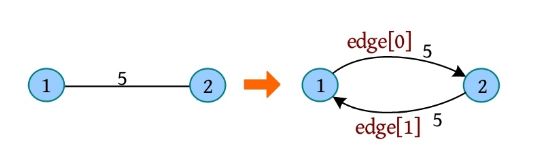
训练1 最大的节点

#includexz@xiaqiu:~/study/algorithm/suanfaxunlian/study$ ./a.out
4 3
1 2
2 4
4 3
4 4 3 4
训练2 有向图D和E

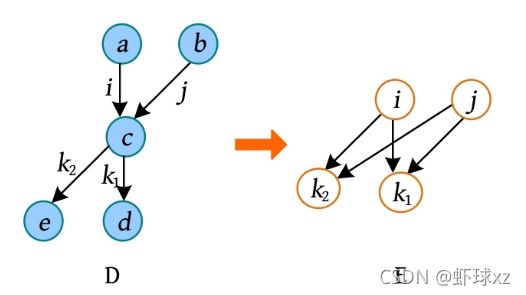
#include 训练3 奶牛排序
bitset<maxn>p[maxn];
if(p[i][k])
p[i]!=p[k];
for(int i = 1;i<=n;i++)
ans+=p[i].count();
cout<<n*(n-1)/2-ans+n<<endl
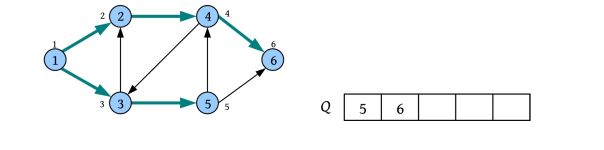
图的遍历
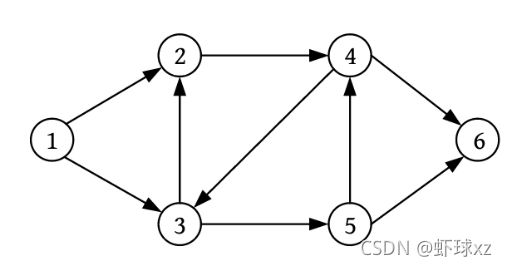
广度优先遍历