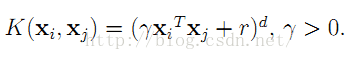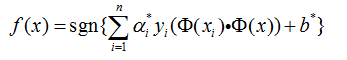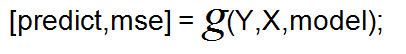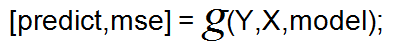支持向量机分类入门实用指南

      支持向量机(SVM)是一种流行的机器学习算法，广泛用于分类问题(也可以用于回归分析)。虽然SVM是比神经网络更容易使用。然而，不熟悉支持向量机的初学者往往不能得到令人满意结果，因为初学者往往错过一些简单但重要的步骤。在本指南中，我们提出了一个简单的操作步骤，通常给出比较理想的结果。

       这个指南不是面向SVM研究人员，也不能保证达到最高的精度。目的是给支持向量机的初学者提供一个快速提升分类器性能的方法。

      用户不需要了支持向量机的理论知识。为了说明我们的步骤，这里简要介绍必要的基本概念。为了得到一个理想的分类器，通常把数据分为训练集和测试集。训练集用来训练分类器，测试集为了测试分类器的性能是否满足要求(误差是否足够小)。每个在训练集的样本包含一个”目标值”(即类标签)和几个”属性”(即特征或观察到的变量)。支持向量机的目标是产生一个基于训练数据的分类模型，该模型可以根据输入的数据属性，预测出数据隶属的标签。

   

支持向量机训练的核心思想：升维和线性化

分类、回归问题来说，很可能在低维样本空间无法线性处理的样本集，在高维特征空间中可以通过一个线性超平面实现线性可分。

但是，升维的同时会带来两个问题

  1)增加计算的复杂性，甚至会引起“ 维数灾难”；

  2)这种变换可能比较复杂，因此这种思路在一般情况下不易实现。

而核函数巧妙地解决了这两个问题

     线性核函数：

  多项式核函数：

  径向基核函数(RBF)：

  Sigmoid核函数：

非线性映射将输入空间的样本映射到高维的特征空间中，训练算法仅使用空间中的点积，即 而没有单独的 出现。

如果找到一个函数K使得

在最优超平面中采用适当的内积函数就可以实现某一非线性变换后的线性可分，而计算复杂度却没有增加。

训练分类器的步骤：

1)将数据转换为支持向量机包的格式

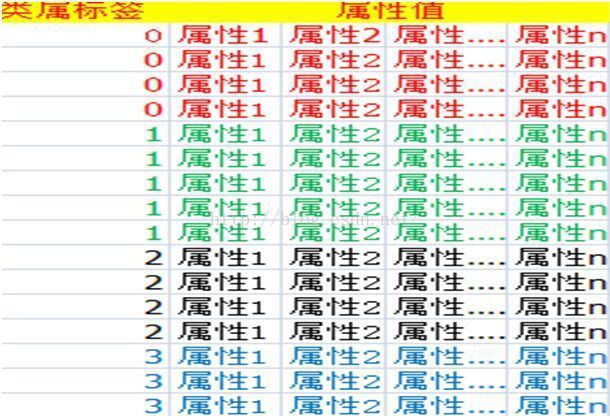
    所谓支持向量机的格式，就是每一条数据由两部分组成，类属标签和属性值，如图

                  

   支持向量机要求每一条数据被表示为实数向量。因此，如果有分类标签，我们首先要      转换成数字数据。建议用m个数据代表m类分类。

2)对数据进行简单的缩放(归一化处理)

   归一化处理非常重要，归一化的主要优点是避免较大的数字属性对较小的数字属性        支配作用。通俗地说，如果属性1的数量级为10³，属性2的数量级为10¹；属性1对分      类器的作用很大，而忽略了属性2的作用。另一个优点是避免在数值计算的困难，大的    属性值可能会导致数值问题。我们建议线性归一化每个属性的范围[-1，1]或[0，1]。

3)优先选择径向基核函数

   在一般情况下，径向基核作为第一选择。径向基核把数据非线性映射到高维空间。线      性核函数是向基核函数的特殊情况，线性核函数的惩罚参数与RBF核函数的参数(C，      r)有相同的作用。对于特定的参数，sigmoid核函数的表现和径向基核函数一样。 

   二是因为，超参数的个数影响训练模型的复杂度，多项式的超参数个数多于径向基核      函数。

  最后，RBF核函数具有较少的数值计算困难，其中关键一点就是，RBF函数中, 在而相比之下，多项式内核值可能会无穷大或者等于零，然而维度会很大。       

   在一些情况下，径向基核函数是不合适的。当数据的维度是非常大的，是使用的线性      核是最好的选择。

4)通过交叉验证选取最佳参数

   用SVM做分类预测时需要调节相关的参数（主要是惩罚参数c和核函数参数g）才能提    高的分类器的准确率。关于SVM参数的优化选取，国际上并没有公认统一的最好的        方法。目前常通过一种交叉验证(CrossValidation,CV)的方法，可以找到在一定意义下    最佳的参数c和g。其基本思想是在某种意义下将原始数据进行分组，一部分作为训练      集，另一部分作为验证集：先用训练集对分类器进行训练，再利用验证集来测试训练      得到的模型，以得到的分类准确率作为评价分类器的性能指标。

    K—fold CrossValidation(K—CV)是常见的CV方法，将原始数据分为K组（一般是均       分），将每个子集数据分别做一次验证集，其余K-1组子集数据作为训练集，这样会       得到K个模型，用这K个模型最终的验证集的回归准确率的平均数作为此K—CV下分类     器的性能指标。K一般大于等于2，实际操作时一般从3开始取，只有在原始数据集合       数据量小的时候才会尝试取2。K—CV可以有效的避免过学习以及欠学习状态的发           生，最后得到的结果也比较具有说服性。

 

   该方法方法就是让c和g在一定的范围内取值，对于取定的c和g，把训练集作为原始数    据集并利用K—CV方法得到在此组c和g下训练集验证回归的准确率，最终取得训练集      验证分类准确率最高的那组c和g作为最佳的参数。如果有多组的c和g对应于最高的验    证回归准确率，这里采用的手段是选取能够达到最高验证回归准确率中参数c最小的那    组c和g作为最佳的参数,如果对应最小的c有多组g,就选取搜索到的第一组c和g作为最      佳的参数。这样的理由是：过高的c会导致过学习状态发生，即训练集回归准确率很高    而测试集回归准确率很低，所以在能够达到最高验证回归准确率中的所有的成对的c和    g中认为较小的惩罚参数c是最佳的选择对象。

5)使用最佳参数训练数据

                 

                 -Model：训练出的分类器

                 -Y：隶属标签

                 -X：属性值

                 -S:SVM类型有两大类，一类用于分类，一类用于回归

                 -t：核函数类型

                 -g：核函数参数

                 -c： 惩罚参数 

6)测试分类器的分类效果(误差率)

                

                 -predict：预测结果

                 -mse：误差 ，根据Y与predict的值计算

                 -Y：测试数据的隶属标签

                 -X：测试数据的属性值

                 -model：训练出的分类器

7)如果测试结果的误差率小于我们期望值，就可以运用该分类器   对数据进行分类

       

    此过程与6)相同，只不过在这里，Y是未知的，mse也没有任何意义了。

LIBSVM工具箱使用方法：

LIBSVM是台湾大学林智仁教授等开发设计的一个简单、易于使用和快速有效的SVM模式识别与回归的软件包，不但提供了编译好的可在Window系列系统的执行文件，还提供了源代码，方便改进、修改以及在其他操作系统上应用。该软件还有一个特点，就是对SVM所涉及的参数调节相对较少，提供了很多的默认参数，利用这些默认参数就可以解决很多问题；并且提供了交互检验(Cross Validation)的功能。该软件包可以在网上免费获得。该软件可以解决C-SVM,nu-SVC,one-class,epsilon-SVR,nu-SVR等问题，包括基于一对一算法的多聚模式识别问题。SVM用于模式识别或回归分析时，SVM方法及其参数、核函数及其参数的选择，目前国际上还没有形成一个统一的模式，也就是说最优SVM算法参数选择还只能是凭经验、实验对比、大范围的搜寻或者利用软件包提供的交互检验功能进行寻优。

LIBSVM下载地址：http://www.csie.ntu.edu.tw/~cjlin/libsvm/index.html

将LIBSVM工具箱所在的目录添加到MATLAB工作搜索目录

具体操作就是将LIBSVM工具箱下载或者复制到某一个目标文件夹后，在MATLAB菜单栏中选择File->Set Path->Add with Subfolders,然后选择之前存放LIBSVM工具箱的文件夹，最后单击save就可以了。

LIBSVM工具箱的主要函数有：

(1)训练函数：

model=svmtrain(train_label, train_data, options);

-train_data:训练集属性矩阵，大小为n×m,n表示样本数，m表示属性数目（维数），数据类型Double。

-train_label:训练集标签，大小为n×1, n表示样本数，数据类型为double。

-options 参数选项。

-model:是训练得到的模型，是一个结构体(如果参数中用到-v，得到的就不是结构体，对于分类问题，得到的是交叉检验下的平均分类准确率；对于回归问题，得到的是均方误差)。

(2)预测函数：

[predict_label,accuracy/mse,dec_value]=svmpredict(test_label,test_data,model);

-test _label表示测试集的标签（这个值可以不知道，因为作预测的时候，本来就是想知道这个值的，这个时候，随便 制定一个值就可以了，只是这个时候得到的mse就没有意义了）。

-test _matrix表示测试集的属性矩阵。

-model   是上面训练得到的模型。

-libsvm_options是需要设置的一系列参数。

-redicted_label表示预测得到的标签。

-accuracy/mse是一个3*1的列向量，其中第1个数字用于分类问题，表示分类准确率；后两个数字用于回归问题，第2个数字表示mse；第三个数字表示平方相关系数（也就是说，如果分类的话，看第一个数字就可以了；回归的话，看后两个数字）。

-decision_values/prob_estimates：第三个返回值，一个矩阵包含决策的值或者概率估计。对于n个预测样本、k类的问题，如果指定“-b 1”参数，则n x k的矩阵，每一行表示这个样本分别属于每一个类别的概率；如果没有指定“-b1”参数，则为n xk*(k-1)/2的矩阵，每一行表示k(k-1)/2个二分类SVM的预测结果。

(3)训练的参数：

-s svm类型：SVM设置类型（默认0)

　　　　0 — C-SVC；

              1  — nu-SVC； 

              2  —  one-class SVM；

              3 — e-SVR； 

              4 — nu-SVR

-t 核函数类型：核函数设置类型（默认2）
　　　　0 – 线性核函数：u’v 
　　　　1 – 多项式核函数：（r*u’v + coef0)^degree
　　　　2 – RBF(径向基)核函数：exp(-r|u-v|^2）
　　　　3 – sigmoid核函数：tanh(r*u’v + coef0)

-d degree：核函数中的degree设置（针对多项式核函数）（默认3）
-g r(gamma）：核函数中的gamma函数设置（针对多项式/rbf/sigmoid核函数）（默认1/k，k为总类别数)
-r coef0：核函数中的coef0设置（针对多项式/sigmoid核函数）（（默认0)
-c cost：设置C-SVC，e -SVR和v-SVR的参数（损失函数）（默认1）
-n nu：设置v-SVC，一类SVM和v- SVR的参数（默认0.5）
-p p：设置e -SVR 中损失函数p的值（默认0.1）
-m cachesize：设置cache内存大小，以MB为单位（默认40）
-e eps：设置允许的终止判据（默认0.001）
-h shrinking：是否使用启发式，0或1（默认1）
-wi weight：设置第几类的参数C为weight*C (C-SVC中的C) （默认1）
-v n: n-fold交互检验模式，n为fold的个数，必须大于等于2

以上这些参数设置可以按照SVM的类型和核函数所支持的参数进行任意组合，如果设置的参数在函数或SVM类型中没有也不会产生影响，程序不会接受该参数；如果应有的参数设置不正确，参数将采用默认值。

参考文献：[1]Chih-Wei Hsu, Chih-Chung Chang, and Chih-Jen Lin.A Practical Guide                         to  Support Vector Classi cation.2010

                  [2]史峰,王小川.MATLAB神经网络43个案例分析[M]. 北京:北京航空航天大学                        出版社 2013.103-153.