关于《数字图像处理》中增强局部图像的两种方法对比及利用C++实现

最近在学《数字图像处理》时注意到利用直方图的两种方法1：局部直方图均衡化 2：直方图统计量   在增强局部图像的效果上有较大的不同，经过网上查阅学习，特在此做一次笔记，对比一下两种方法对图像增强效果的差异。

直方图处理技术可以用于局部增强。过程是定义一个邻域，并把该区域的中心从一个像素移至另一个像素。在每个位置，计算领域中点的直方图，并且得到的不是直方图的均衡化就是规定化的变换函数，这个函数最终用于映射邻域中心像素的灰度。之后，领域的中心移动到下一个相邻像素点，一直重复该过程。当邻域进行逐像素平移时，由于只有邻域中的一行或一列改变，所以可以在移动一步中，以新数据更新前一个位置得到的直方图。因此局部增强可体现更多的图像细节。

---

先来看局部直方图均衡化：

原理：分为子块不重叠、子块重叠和子块部分重叠，函数中可选择不同的方法计算。

子块不重叠算法：根据输入分割子块的大小为n，将图像划分为多块n*n大小的子块，单独对每块进行直方图均衡化，局部细节对比度因此而得到增强，但可能会导致有各子块区域的直方图均衡函数差异较大，会出现块效应；

子块重叠算法：根据输入分割子块的大小n,利用该分割子块的直方图信息对子块中心的像素进行均衡化，之后遍历输入图像所有像素；

子块部分重叠算法：子块是将移动步长约取为子块尺寸的几分之一而不是逐一像素移动，子块均衡的灰度值用于映射子块所有像素的灰度值，并记录对多次被均衡的像素，将均衡结果取平均作为该像素在输出图像中的灰度值，因此块效应基本消除，且由于不是遍历像素移动因此效率大大提升。

函数实现的代码如下：

#include   
#include 
#include 

using namespace std;
using namespace cv;


//直方图均衡化，ksize - 块大小，kstep - 块中心步进
int LocalEqualHist(const Mat& input, Mat& out, int ksize, int kstep = 1);



int main(int argc, char** argv)
{
	Mat src;				//原图
	Mat dst;					//处理后的图片
	Mat gray_Hist;				//灰度直方图
	vector histogram;	//灰度直方图数据

	//载入原图（灰度图方式）
	src = imread("D:\\folder\\数字图像处理Image\\CH03\\1.tif", 0);

	//图片处理
	LocalEqualHist(src, dst, 3);

	//创建窗口
	namedWindow("【原图】");
	namedWindow("【处理后】");

	//显示图片
	imshow("【原图】", src);
	imshow("【处理后】", dst);

	//保存图片
	//imwrite("3-26_c.tif", im_pro);

	//等待键盘操作
	waitKey(0);

	return 0;
}

//局部直方图均衡化函数声明
int LocalEqualHist(const Mat& input, Mat& out, int ksize, int kstep)
{
	int h{ input.rows };				// 图片高
	int w{ input.cols };				// 图片宽
	uchar* data_in{ input.data };		// 原图图片像素数据
	uchar* data_out;					// 输出图片像素数据
	double* d_data_out;					// 输出图片像素数据
	int* n_data;						// 各像素值累加重叠次数
	double* s;							// 灰度映射
	long* hist;							// 灰度直方图数据
	vector indexs_hist;			// 灰度直方图对应灰度值索引
	int index_hist;						// 灰度直方图对应灰度值索引
	int size_index;						// 直方图索引长度	
	int bit_dep;						// 位比特数
	int halfsize{ ksize / 2 };			// 一半领域大小
	int i, j, x, y, u, v;				// 循环变量

	//参数输入错误
	if (h < ksize || w < ksize || kstep <= 0)
		return 0;

	//输出图像初始化
	out.release();
	out = Mat::zeros(h, w, input.type());
	data_out = out.data;
	d_data_out = new double[h * w]{};
	n_data = new int[h * w]{};

	// 获取比特数
	switch (input.depth())
	{
	case CV_8U:
		bit_dep = 256;
		break;
	case CV_16U:
		bit_dep = 65536;
		break;
	default:
		break;
	}

	hist = new long[bit_dep] {};
	s = new double[bit_dep] {};

	//进行局部直方图均衡化变换
	for (v = halfsize; v < h - halfsize; v += kstep)
		for (u = halfsize; u < w - halfsize; u += kstep)
		{
			//统计局部直方图
			index_hist = data_in[v * w + u];
			indexs_hist.push_back(index_hist);
			for (y = v - halfsize; y <= v + halfsize; y++)
				for (x = u - halfsize; x <= u + halfsize; x++)
				{
					//统计索引
					index_hist = data_in[y * w + x];
					size_index = indexs_hist.size();

					if (index_hist == indexs_hist[size_index - 1] || index_hist == indexs_hist[0])
						;
					else if (index_hist > indexs_hist[size_index - 1])
						indexs_hist.push_back(index_hist);
					else if (index_hist < indexs_hist[0])
						indexs_hist.insert(begin(indexs_hist), index_hist);
					else
					{
						for (i = 1; i < size_index; i++)
							if (index_hist == indexs_hist[i])
								break;
							else if (index_hist < indexs_hist[i] && index_hist > indexs_hist[i - 1])
							{
								indexs_hist.insert(begin(indexs_hist) + i, index_hist);
								break;
							}
					}
					//统计局部直方图
					hist[index_hist]++;
				}

			//计算映射
			for (i = 0; i < (int)indexs_hist.size(); i++)
				for (j = 0; j <= i; j++)
					s[indexs_hist[i]] += (double)(bit_dep - 1) / (ksize * ksize) * hist[indexs_hist[j]];

			//映射灰度值
			for (y = v - halfsize; y <= v + halfsize; y++)
				for (x = u - halfsize; x <= u + halfsize; x++)
				{
					d_data_out[y * w + x] += s[data_in[y * w + x]];
					n_data[y * w + x]++;
				}

			//清空直方图及映射
			for (int& m : indexs_hist)
			{
				hist[m] = 0;
				s[m] = 0;
			}
			//清空索引
			indexs_hist.clear();
		}

	//转换灰度值
	for (int y = 0; y < h; y++)
		for (int x = 0; x < w; x++)
		{
			if (n_data[y * w + x] != 0)
				data_out[y * w + x] = cvRound(d_data_out[y * w + x] / n_data[y * w + x]);
			else
				data_out[y * w + x] = data_in[y * w + x];
		}

	delete d_data_out;
	delete n_data;
	delete hist;
	delete s;
	return 1;
}

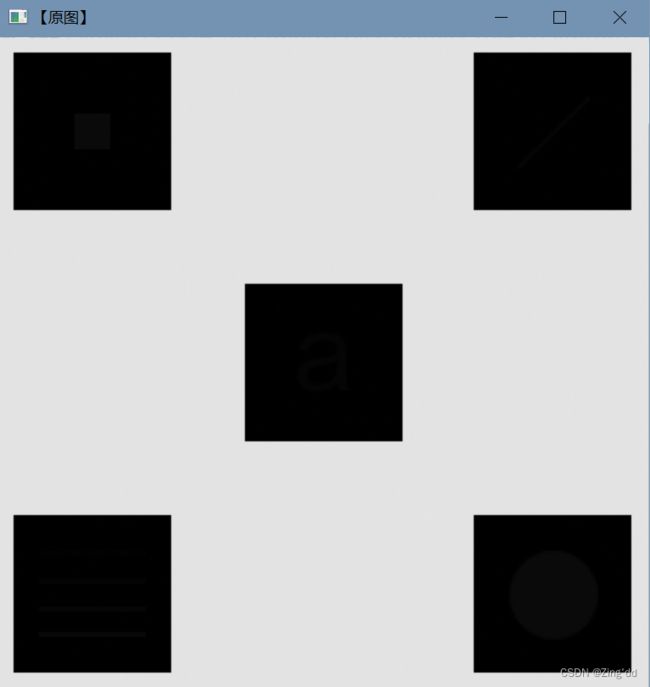
运行之后两图的对比，在原图五个黑块中隐藏着五个不同图案，因为灰度值与黑块部分十分接近，故全局直方图均衡化后不能处理出这些细节，而经过局部直方图均衡化后可以清晰看到黑色方格内的重要细节。但整张图片可改变了颜色，还出现许多噪点，隐藏图案只剩下轮廓可见。

---

下面来看利用直方图统计量来增强局部图像：

所以用的原理公式详见冈萨雷斯《数字图像处理》第四版，这里我只讲一个公式。

公式意思是定义一个3×3的邻域，平均局部灰度和局部标准差都处在一定范围内，则此像素的值乘上系数C，增大（活减小）相对于图像身下部分的灰度值，否则此像素保持不变。

这里引用知乎博主的一个详细解释，附上原文链接：局部直方图处理：直方图统计

首先我们要将对比度低区域找出来，怎么找呢？我们需要一个比较！我们知道方差体现了一个区域内数值的差距大小，若该区域亮度值相等，则方差为0，而对比度较低区域的方差通常也很小。我们用前面设置的3x3邻域遍历整张图片的每一个像素值，每一次都求一次方差和均值。

注：红色框是左上角方块中隐藏图案；黄色框是该邻域未接近隐藏图案；蓝色框是邻域进入隐藏图案

我们先算出红色框的均值和标准差分别为：35.4，5.5。再算出蓝色框的均值和方差：39.9，4.4。随着邻域进入隐藏图案，方差也会越来越小，我们是否可以用刚进入邻域的方差作为一个阈值呢？只有当该点(c,d)邻域方差小于这个阈值时，我们才提高该点(c,d)的亮度。因此我们k3,即方差最大值可以选择(4.4/原图标准差)。因此，在我们进行遍历的时候，均值在进入区域也会变大。如果方差小于k3时，我们就要将该点像素提高。如何提高呢？这就是系数C的作用了。k2的取值通常为0，因为因此图案中也有方差为0的地方。

系数C的定义就是（max(原图) / max(邻域)），目的就是提高对比度低区域（隐藏图案）的亮度。假设原图最高亮度是200，该邻域最高亮度为20，则200/20=10，我们乘10后，隐藏图案该像素值就会变亮，但不会超过全图最高亮度。

这样我们能够找到对比度较低的地方并处理，但是均值是干嘛的呢？

左边对应原图中的白色区域，右图对应原图黑色区域

我们可以看到无论白色还是黑色区域，区域内亮度值基本相同，如果用方差判断的话他们也会被认定为低对比度区域。但是我们通过求两部分均值：230，32。再跟前面的均值对比，发现不是比目标区域的低就是高。因此我们可以通过均值大小来更加精准的来判断是否为隐藏图像区域。只有均值和方差均满足条件时，才提高亮度。那么k1上线应该选择（隐藏区域最大均值/原图均值）。下限k0通常选择（隐藏区域边界最小均值/原图均值）。这样我们就过滤了黑色和白色区域。

通过上述公式，遍历整张图片，仅改变隐藏图案亮度，我们就会得到处理后的图片。

相关函数实现的代码如下：

#include 
#include

using namespace std;
using namespace cv;

double getMean(double* r_pdf) {
    double m = 0;
    for (int i = 0; i < 256; i++)
        m += i * r_pdf[i];
    return m;
}

double getVariance(double* r_pdf, double m)
{
    double delta = 0;
    for (int i = 0; i < 256; i++)
        if (r_pdf[i] != 0)
            delta += (pow((i - m), 2) * r_pdf[i]);
    return delta;
}

void init(double* r_pdf) {
    for (int i = 0; i < 256; i++) {
        r_pdf[i] = 0;
    }
}

int histStatistic(cv::Mat& src, int dim, float k0, float k1, float k2, float E) {
    if (dim % 2 == 0) {
        return -1;
    }

    int width = src.rows;
    int height = src.cols;
    int mn = width * height;
    double r_pdf[256] = {};
    for (int row = 0; row < src.rows; row++) {
        for (int col = 0; col < src.cols; col++) {
            int g = src.at(row, col);
            r_pdf[g] += 1.0 / mn;
        }
    }

    double mean = getMean(r_pdf);
    double delta = getVariance(r_pdf, mean);
    double delta1 = std::sqrt(delta);
    double mxy = 0;
    double deltaxy = 0;
    double local = dim * dim;
    for (int i = dim / 2; i < height - dim / 2 - 1; i++)
    {
        for (int j = dim / 2; j < width - dim / 2; j++) {
            init(r_pdf);
            //统计局部直方图
            for (int p = j - dim / 2; p < j + dim / 2 + 1; p++) {
                for (int q = i - dim / 2; q < i + dim / 2 + 1; q++) {
                    int g = src.at(p, q);
                    r_pdf[g] += 1.0 / local;
                }
            }
            mxy = getMean(r_pdf);
            deltaxy = getVariance(r_pdf, mxy);
            double deltaxy1 = sqrt(deltaxy);
            if (mxy <= mean * k0 && deltaxy1 <= k2 * delta1 && deltaxy1 >= k1 * delta1) {
                src.at(j, i) = src.at(j, i) * E;
            }
        }
    }
}

int main() {
    Mat src = cv::imread("D:\\folder\\数字图像处理Image\\CH03\\1.tif", 0);
    Mat dst;
    dst = src.clone();
    histStatistic(dst, 7, 0.4, 0.02, 0.4, 10);
    imshow("src", src);
    imshow("dst", dst);
    waitKey(0);
}

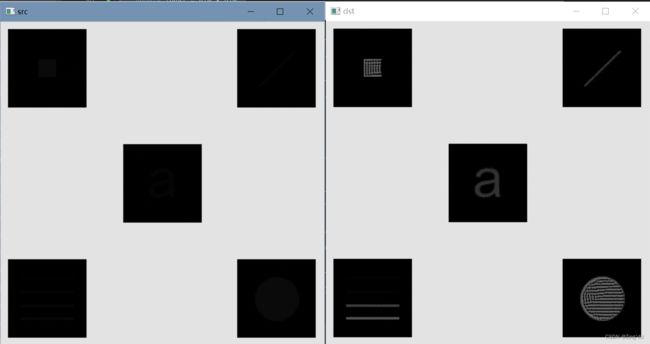
运行之后得到的目标图（左为原图，右为目标图）：

        由结果可知，采用直方图统计量能提取出更多的细节，且在其他灰度区域无明显变化，只提取出了我们想要的信息。相比之下，利用局部直方图均衡化出现了更多明显的噪声，且失去了原有的灰度级内容。故，在增强局部图像上使用直方图统计量要优于局部直方图均衡化。