OpenGL 坐标系统详解

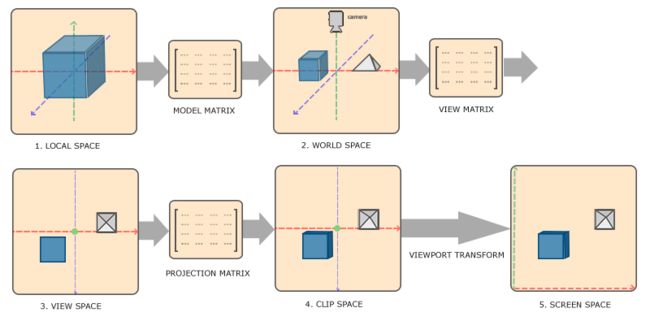
GL中的坐标系是标准设备坐标，即他的每个坐标轴的取值范围都是[-1.0,1.0]。通常，我们输入到顶点着色器中的顶点坐标都会被转换为标准化设备坐标，然后进行光栅化，转变成屏幕坐标。然而事实上，从顶点坐标到屏幕坐标是一个较为复杂的过程。总体来讲为了某些计算更加方便，会经过5个坐标系统的变换：

• 局部空间(Local Space，或者称为物体空间(Object Space))

• 世界空间(World Space)

• 观察空间(View Space，或者称为视觉空间(Eye Space))

• 裁剪空间(Clip Space)

• 屏幕空间(Screen Space)

下面就是坐标系统的具体意义。

1. 概述

经过了这么久的介绍，我们都一直在绘制屏幕中的一个矩形。而事实上，之前的一切过程，我们还只是停留在建造模型的过程。这时候我们的画布里只有这一个模型，我们把当前的坐标系统称作是局部空间。

当然，我们的屏幕中大多数情况下不可能只有一个模型，而是千千万万个模型。我们应该通过一系列矩阵变换将模型变换到一个更大的画布中。当然，我们的屏幕是不可能变大的，所以我们是通过一系列的矩阵缩放我们的模型然后放到原始画布中来模拟把模型放入大画布中这个过程。这里，我们把变换到大画布后的坐标系统称为是世界空间。而从局部空间变换到世界空间转换所需要的这个矩阵，我们成为模型矩阵。

我们知道，OpenGL是一个3维的世界，然而我们屏幕是一个2维的画面。就好像我们生活在3维空间中但是我们所观察的世界实际是以我们的眼睛作为起始点获取的3维空间在我们的视网膜上投影在将信息传给我们的大脑。那么OpenGL模拟了这个过程，首先我们需要一个眼睛，再其次我们需要将世界投影到我们的屏幕上。

在OpenGL中我们把这个眼睛称作是摄像机。而摄像机针对的坐标系统称为观察空间。我们从世界空间转换到观察空间所经过的矩阵为观察矩阵。经过观察矩阵转换后，实际上我们看到的就是3维世界在我们摄像机所面对的方向上的一个投影了。

生活中我们有一个常识，物体*大远小。物体距离我们越远，他看起来将会越小，我们把这种现象称为透视现象。然而在观察空间我们看到的投影缺不具备这种特点，我们把这种按照物体原比例显示的投影称为正投影。然而这样的投影却与我们*常所观察到的世界不一样，为了让事物看起来更加真实，我们要给物体加上透视效果。经过透视的投影，就是透视投影。GL中，我们为了使物体具有透视效果，我们要将物体经过一个透视投影矩阵进行转换，转换至的空间我们称为裁剪空间。之所以称为裁剪空间，是因为除了投食之外，我们还要把超出视野的地方裁减掉。而GL中就是把超出屏幕空间的物体裁减掉。所以称之为裁剪空间。

最后，我们要把裁剪空间中的物体转换到我们的屏幕上进行输出。屏幕输出的空间我们叫做屏幕空间。这个过程呢，就不用我们费心了，因为到了裁剪空间之后我们已经完全完成了模型到透视投影的转换。接下来只需要将这部分物体展示在屏幕上就好，所以这部分工作由GL替我们完成。这个过程，我们叫视口变换。视口变换将位于-1.0到1.0范围的坐标变换到由glViewport函数所定义的坐标范围内。最后变换出来的坐标将会送到光栅器，将其转化为片段。

到这里我们已经大概清楚了这些空间的作用，那么在对应空间中的坐标就分别称为局部坐标(Local Coordinate)、世界坐标(World Coordinate)、观察坐标(View Coordinate)、裁剪坐标(Clip Coordinate)和屏幕坐标(Screen Coordinate)。

2. 组合

我们知道，从我们的局部空间到屏幕空间需要我们先把局部坐标转换至裁剪坐标，再交由GL转换为屏幕坐标。所以我们应该经过的过程就是：

顺序一定不要搞错，记住矩阵乘法是从右向左的。

3. 进入3D

这里我就不放全部代码了，先放一段模型构建的代码

 void configVAO(unsigned int * VAO,unsigned int * VBO,unsigned int * EBO) {
    ///顶点数据
    float vertices[] = {
        0.5,0.5,0.5,0.0,0.0,0.0,
        0.5,-0.5,0.5,1.0,0.0,0.0,
        -0.5,-0.5,0.5,0.0,1.0,0.0,
        -0.5,0.5,0.5,0.0,0.0,1.0,
        0.5,0.5,-0.5,1,1,1,
        0.5,-0.5,-0.5,0,1,1,
        -0.5,-0.5,-0.5,1,0,1,
        -0.5,0.5,-0.5,1,1,0
    };

    ///索引数据
    unsigned int indices[] = {
        0,1,2,
        0,2,3,
        1,4,5,
        0,1,4,
        5,6,7,
        4,5,7,
        2,3,6,
        3,6,7,
        0,3,4,
        3,4,7,
        1,5,6,
        1,2,6,
    };

    ///创建顶点数组对象
    glGenVertexArrays(1, VAO);

    ///创建顶点缓冲对象
    glGenBuffers(1, VBO);
    ///创建索引缓冲对象
    glGenBuffers(1, EBO);

    ///绑定定点数组对象至上下文
    glBindVertexArray(*VAO);

    ///绑定定点缓冲对象至上下文
    glBindBuffer(GL_ARRAY_BUFFER, *VBO);
    ///把顶点数组复制到顶点缓冲对象中
    glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);
    ///设置顶点属性并激活属性
    glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 6 * sizeof(float), (void*)0);
    glEnableVertexAttribArray(0);
    glVertexAttribPointer(1,3,GL_FLOAT,GL_FALSE,6 * sizeof(float), (void*)(3 * sizeof(float)));
    glEnableVertexAttribArray(1);
    ///绑定索引缓冲对象至上下文
    glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, *EBO);
    ///把索引数据复制到索引缓冲对象中
    glBufferData(GL_ELEMENT_ARRAY_BUFFER, sizeof(indices), indices, GL_STATIC_DRAW);

    ///解除顶点数组对象的绑定
    glBindVertexArray(0);
    ///解除顶点缓冲对象的绑定
    glBindBuffer(GL_ARRAY_BUFFER, 0);
    ///解除索引缓冲对象的绑定
    glBindBuffer(GL_ELEMENT_ARRAY_BUFFER,0);
}

上面我们建立了一个正方体，八个顶点分别有八个颜色。目前，他还在局部空间内。

接下来我们来将他们转换到裁剪空间内：

glm::vec3 postions[] = {
    glm::vec3(0.0,0.0,0.0),
    glm::vec3( 2.0f,  5.0f, -15.0f),
    glm::vec3(-1.5f, -2.2f, -2.5f),
    glm::vec3(-3.8f, -2.0f, -12.3f),
    glm::vec3( 2.4f, -0.4f, -3.5f),
    glm::vec3(-1.7f,  3.0f, -7.5f),
    glm::vec3( 1.3f, -2.0f, -2.5f),
    glm::vec3( 1.5f,  2.0f, -2.5f),
    glm::vec3( 1.5f,  0.2f, -1.5f),
    glm::vec3(-1.3f,  1.0f, -1.5f)
};

glm::mat4 view = glm::mat4(1.0f);
view = glm::translate(view, glm::vec3(0.f, 0.f, -3.f));
glm::mat4 projection = glm::mat4(1.0f);
projection = glm::perspective(glm::radians(45.0f), (float)(SCR_WIDTH * 1.0 / SCR_HEIGHT), 0.1f, 100.0f);
ourShader.setMtx4fv("view", view);
ourShader.setMtx4fv("projection", projection);

while (!glfwWindowShouldClose(window))
{
    processInput(window);

    ///设置清屏颜色
    glClearColor(0.2f, 0.3f, 0.3f, 1.0f);
    ///清屏
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

    ///绑定定点数组对象
    glBindVertexArray(VAO);

    for (int i = 0; i < 10; ++i) {
        glm::mat4 model = glm::mat4(1.0f);
        model = glm::translate(model, postions[i]);
        float angle = 20.0f * i;
        model = glm::rotate(model, glm::radians(angle), glm::vec3(1.0f, 0.3f, 0.5f));
        ourShader.setMtx4fv("model", model);

        ///以索引绘制顶点数据
        //        glDrawArrays(GL_TRIANGLES, 0, 3);
        glDrawElements(GL_TRIANGLES,36,GL_UNSIGNED_INT,0);
    }


    ///交换颜色缓冲
    glfwSwapBuffers(window);
    ///拉取用户事件
    glfwPollEvents();
}

我们看到，我们为每个物体定单独定义了一个模型矩阵，这样，我们每个模型在世界空间中的状态都不同，然后在定义了唯一一个观察矩阵和透视投影矩阵，这样就模拟出我看眼睛看到物体的一个过程。

这里我们只对glm为我们提供的几个新出现的函数做一下简单讲解：

这是用来指定透视投影矩阵的函数。

• 第一个参数radians指的是Fov，它表示的是视野(Field of View)，并且设置了观察空间的大小。如果想要一个真实的观察效果，它的值通常设置为45.0f。他就是图中两个蓝色实线的空间夹角。

• 第二个参数scale设置了宽高比，由视口的宽除以高所得。

• 第三和第四个参数设置了*截头体的*和远*面。我们通常设置*距离为0.1f，而远距离设为100.0f。所有在**面和远*面内且处于*截头体内的顶点都会被渲染。图中粉色截面即为**面，蓝色截面即为远*面。

接下来虽然代码中没有，我们还是提一下正投影矩阵的创建方法：

 当你把透视矩阵的 near 值设置太大时（如10.0f），OpenGL会将靠*摄像机的坐标（在0.0f和10.0f之间）都裁剪掉，这会导致一个你在游戏中很熟悉的视觉效果：在太过靠*一个物体的时候你的视线会直接穿过去。

文章转载自：rmb_999

原文链接：https://www.cnblogs.com/rmb999/p/17815403.html